基于多维数据挖掘的讲评课方案的优化<br/>——以拉萨市高中数学试卷讲评为例

基于多维数据挖掘的讲评课方案的优化
——以拉萨市高中数学试卷讲评为例

2023-08-10陈佳莉拉萨师范高等专科学校数学和自然科学系

西藏教育 2023年7期

陈佳莉拉萨师范高等专科学校数学和自然科学系

小巴桑次仁西藏大学理学院

一、背景介绍

有关西藏数学教育研究方面，很多学者从双语教育、教学教法、信息技术等角度做了一定的研究［1］，但是针对西藏教育环境下开展的试卷讲评课的研究几乎为零。试卷讲评课是教学整体流程的一个重要环节，能很好地评价学生“学”与教师“教”的效果，高效的试卷分析是提高讲评课质量的重要保障。当前国内有关“试卷分析”和“试卷讲评课”的研究强调了试卷分析的深度和讲评课各流程设计的科学性［2-3］，但是试卷分析与讲评课设计往往被作为两个独立的课题研究项目，未将上述两个概念间的连续性与整体性作为研究对象；此外也有部分研究人员对讲评课的一般性理论［4］，如讲评模式与讲评原则等做了一般性陈述，但缺少一定的实践性和针对性。

基于以上分析，本文首先通过定量与定性相结合的分析方法得到试卷质量分析报告。试卷用于拉萨市高中生的数学考试，提炼试卷数据后借助WEKA平台的K-means 算法获得了以讲评课设计为导向的试卷分析结果，从而初步确定了讲评材料设计与学生分组方案。在此基础上，结合访谈、问卷以及试卷反思数据，综合分析确定了最终的试卷讲评材料和分组方案；将Apriori算法应用于讲评备选试题的分析可获得题目间的关联关系，进而通过平移方法可得到相应知识点间的关联程度，从而为讲评课方案的设计提供重要依据。

二、数据来源及预处理

本文数据主要由学生调查问卷、教师访谈、学生试卷反思表以及试卷数据四部分构成，各部分的分析情况如下。

（一）学生调查问卷与教师访谈数据

西藏自治区拉萨市目前有6所高中，高中在校生13076人（2020年度），样本数量依据如下有限样本估计公式［5］确定：

其中n为样本数，N为总体数量,α为显著性水平，k为置信度所对应的分位数，p为样本估计的显著性。当α=0.05 时，可得k=1.96，P=0.5，从而样本需求量为n ≥373。为进一步避免抽样误差，研究依据2019-2020 两年的统考成绩对学校、班级分别进行优、中、差排序，经分层抽样，确定了调查对象为3 所学校的9 个班级。调查发放问卷400 份，收回381 份，其中有效问卷374 份，问卷有效回收率为98.16%。

学生调查问卷和教师访谈稿由4 个维度组成，包括对讲评课的认识与态度、讲评课前、讲评课中和讲评课后的现状。通过数据分析，问卷克隆巴赫系数为0.715，效度为0.739，属于可接受范围之内。学生调查问卷和教师访谈信息的汇总与对比如表1所示。

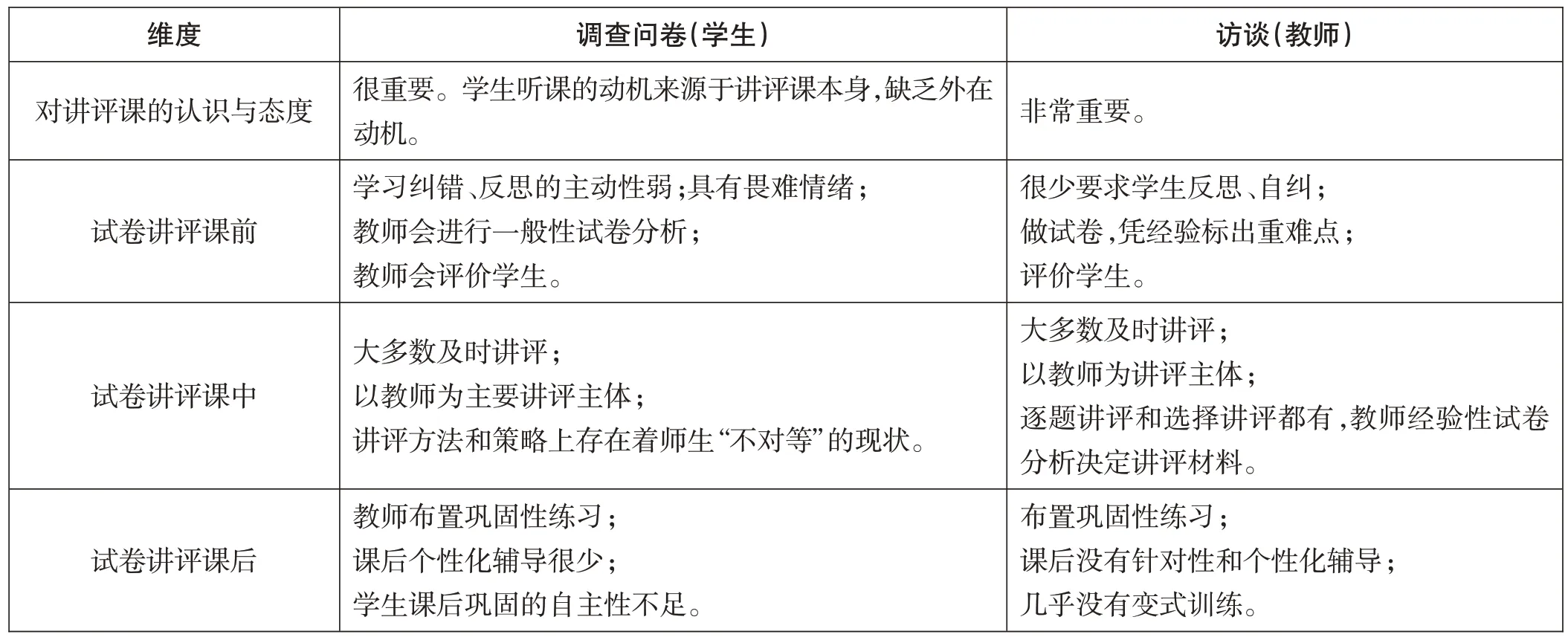
表1 调查问卷与访谈稿结果汇总对比

表1 反映出拉萨市数学试卷讲评课存在以下主要问题：1.学生学习主动性弱，很少进行纠错反思，具有畏难情绪；2.教师试卷分析的程度较浅；3.试卷讲评课设计形式单一、内容简单；4.讲评方法存在师生“不对等”现状；5.个性化讲评有待加强。

基于调查问卷和访谈稿中所反映出的问题，本文将通过设计学生试卷反思表解决表1 中的1、4、5 问题。

（二）学生试卷反思表

归因理论认为学生对成败的正确归因有助于刺激学生的学习动机。学生试卷反思表是学生从自身的角度出发对试题进行归类，以此帮助教师了解学生对讲评的需求，增强讲评课设计的针对性。本研究设计了具有5 个维度的学生试卷反思表，分别为：对而不会的题、会而不对的题、完全不会的题、过失性失分的题和期待讲评的题。

被试班级学生试卷反思数据如图1 所示，体现了学生期待讲评的试题与完全不会的试题间的对比，从中得知，完全不会题目人数的最值处（包括最大与最小）获得学生期待讲评的最低值，比如难度最高得分率最低的21、22 题，学生期待值较低，说明被试班级学生具有畏难情绪，该现象与问卷（表1）调查讲评课前学生行为研究中反映出的“学生学习反思、纠错的主动性弱，具有畏难情绪”相吻合。依据各题期待讲评的人数与讲评课设计的课时要求结合分析，确定学生最希望讲评的8 道试题，并与试卷数据分析结果进一步比对后最终确定是否以及如何纳入讲评材料。

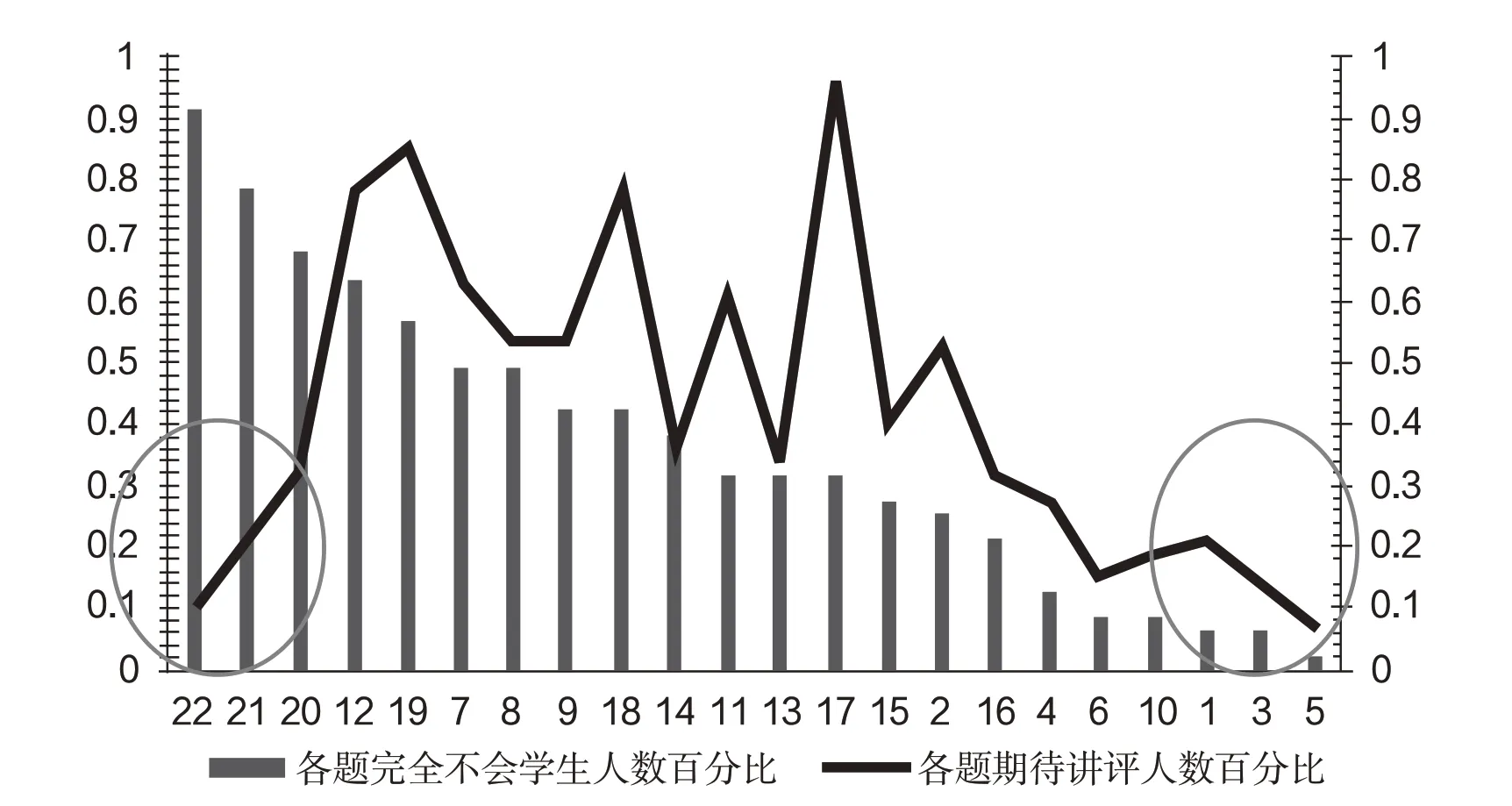
图1 学生数学试卷反思表可视化

（三）试卷数据

1.被试班级与试卷背景介绍

本研究所选择的被试班级为拉萨市某中学高三年级的理科班，共47名学生。本次测试学校自主命题，其目的是为了了解学生在高中三年内对数学知识的整体掌握情况，因此试卷命题具有难度大、范围广的特点。试卷包括22道题，覆盖高考大纲（理科数学）中的各模块，其中平面解析几何、立体几何初步和数列部分占比最重；在“题型结构”模块，各种题型均有涉及，且各题型分值服从标准试卷设计分布；在“知识要求”模块中,“了解；理解；掌握”分值按3:4:3的比例分布。整卷信度为0.62，具有信度；区分度为0.26，试卷质量合格，整体难度值为0.36，说明本次测试相当困难。［6］

2.试卷数据前处理

由于在网络试卷评阅中每个填空题被视为一道题，体现不出各试题的个性特质，因此略去填空题对应的数据；为了确保试卷的质量，本文选取难度值高于0.2的试题进行分析，从而确定可应用于进一步数据分析的纬度为48×15的试卷数据矩阵C，其中“行”代表样本（学生），“列”代表变量（题目）。将数据矩阵C导入用于数据分析的WEKA平台，进行了二值离散化处理。

三、深度试卷分析

（一）基于K-means算法的试卷分析

K-means算法是一种用于分组的经典数据分析方法，本文首先将K-means算法应用于前处理后的二值离散数据，依据学生完成试题的情况将被试班级学生进行分组，分组信息包括确定每组人数、每组学生编号和存在问题的对应题目。通过总结各组的分组特点获取精准的讲评材料和个性化讲评依据，如表2所示。

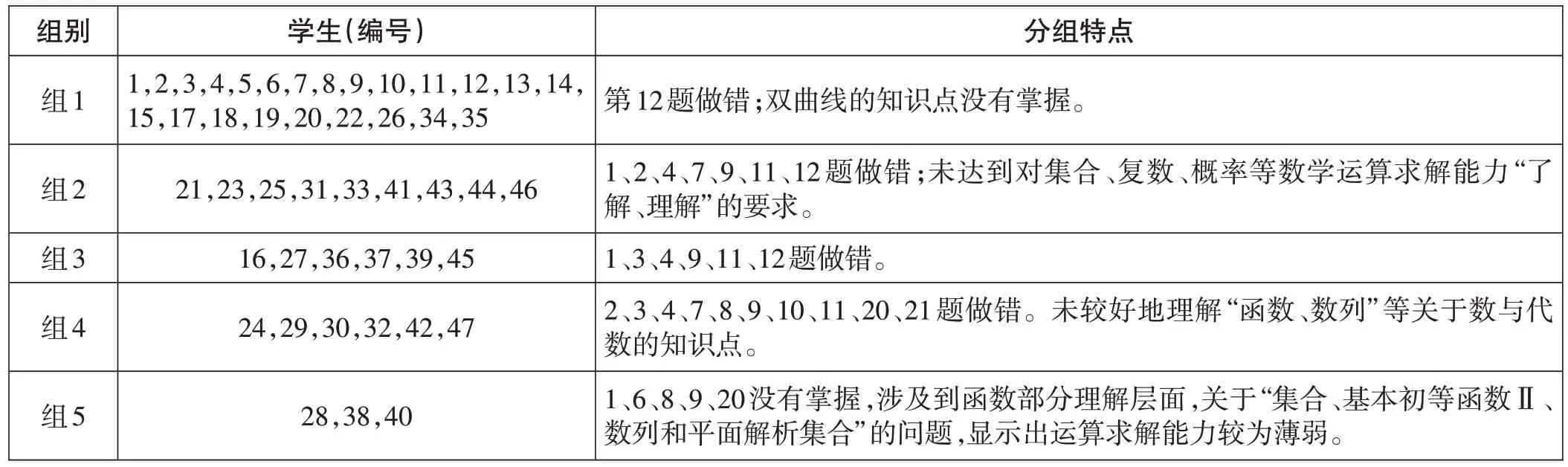
表2 K-means分组（按人数降序排列）

基于解决全班大部分学生存在的问题为主要目的，将前三组存在问题的题目进行汇总，并根据每道题错误的人数对试题进行降序排列，按照课时安排（1课时），选择前8道题作为讲评预设材料，并与学生试卷反思表结果进行进一步比对。

（二）基于Apriori算法的深度试卷分析

Apriori 算法是数据分析领域解决关联规则的常用算法，其主要原理为通过求解频繁项集的方式挖掘研究对象之间的关联规则。将Apriori 算法应用于被试班级测试卷后提取试题间的关联规则和关联置信度，根据关联规则和置信度强弱构建试题关联图，再将试题与测试双向细目表对比后，可平移得到相应知识点的关联图以及知识云图中各知识点之间的关联程度，从而为试题的讲评顺序、分块讲评、时间安排等方面提供重要的参考依据。

四、基于综合分析构建的讲评课设计方案

本文依据迪克与凯里的教学系统设计模型，通过调定顺序、步骤修正、形成循环三个阶段，建立了以讲评课性质为基础的讲评课设计流程（如图2 所示）。通过K-means 算法与学生数学试卷反思表确定讲评材料的基础上分析材料的知识点、知识水平和数学能力要求，确定讲评目标；利用Apriori 算法对确定后的讲评材料进行关联分析，确定讲评策略。

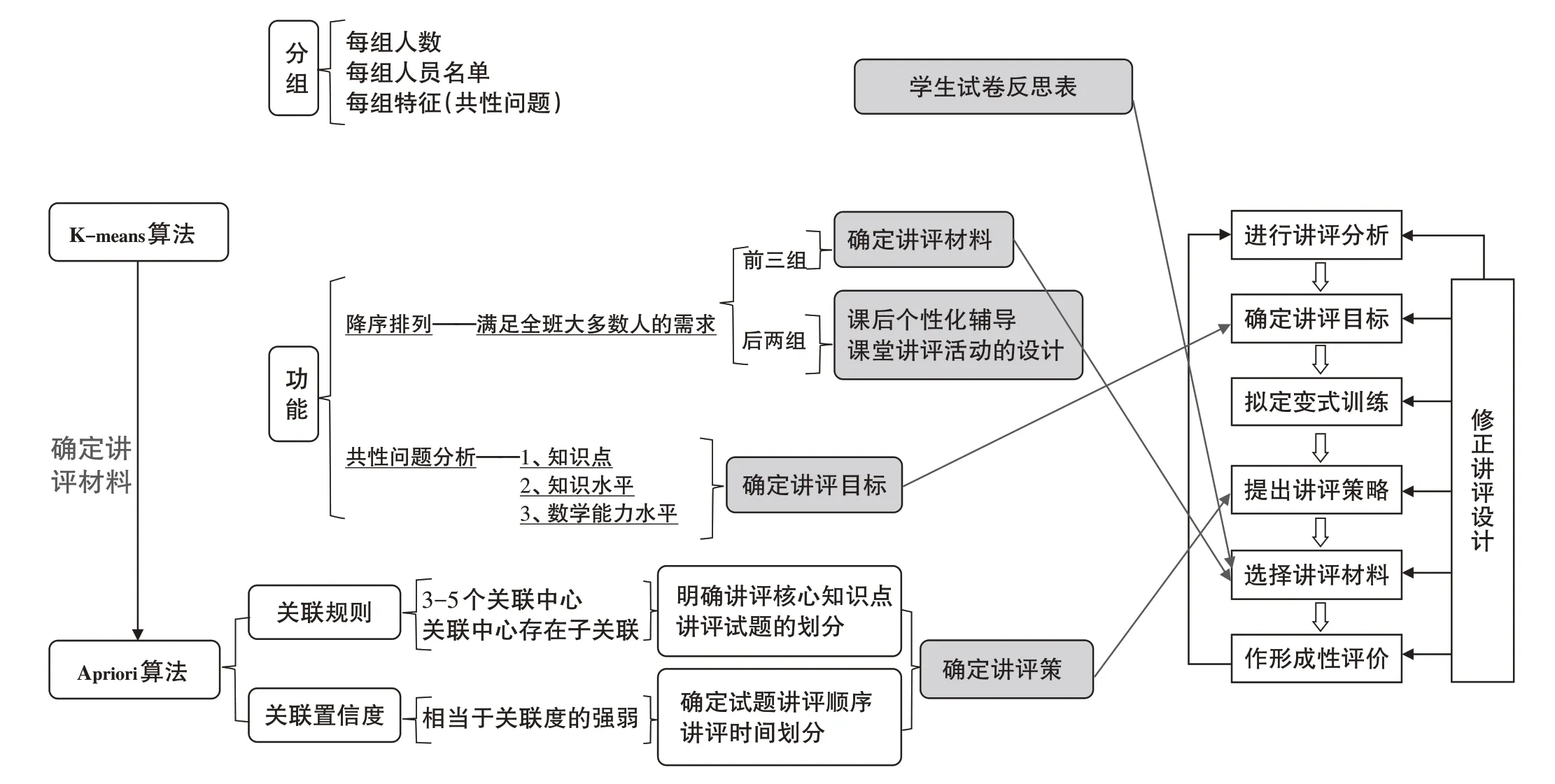
图2 试卷分析与讲评课设计的关联

（一）讲评材料的选取

学生试卷反思表确定的学生期待讲评的试题与K-means算法分析出分组后学生前3组存在问题的试题对照如表3所示：

表3 被试班级试卷讲评题目对比（部分）

对比发现题目2、7、9、11、12在两种情况中都存在，因此该5道题目为必讲材料且优先讲授；题目17、18、19属于较难题目且学生有讲评需求，因此列为必讲材料并在前述5道题之后讲解；学生出现错误较多但是无讲评需求的题目为1、3、4，因此列为选择性讲评内容。

（二）讲评策略

对已确定的讲评材料进行关联挖掘，得到试题间的关联规则和关联置信度，通过平移可得到知识点间的关联置信度。如图3所示，讲评材料中三角函数的图像是核心知识点，与三角函数的和差化积、向量加减法及其几何意义和复数的四则运算关系最近，关系最远的是等比数列。因此，初步确定讲评策略为主题式讲评，以“三角函数的图像”为主题，利用思维导图将知识点进行串联，构建知识体系。

图3 Apriori算法下筛选后试题的知识关联云图

五、建议

针对调查问卷和教师访谈中所反映出来的当前拉萨市数学试卷讲评课的问题，本研究提出以下建议：

（一）阅卷时尽量录入试卷较详细的数据信息，构建试卷数据库

试卷数据库的建立有助于教师从横向空间分布与纵向时间分布掌握试卷命制的变化趋势、学生学习能力的变化趋势，精确定位学生考试所存在的核心问题，针对性制定讲评课内容和教学计划。当前拉萨市大部分高级中学在大型考试中的阅卷以网络阅卷的形式开展，可以获得每道试题的具体得分信息，因此，为构建试卷数据库创造了很好的条件。但在校级考试或者一般性考试中，阅卷主要为线下阅卷，因此需要手动录入较详细的信息。

（二）对一线教师进行教育测量和软件使用的培训

调查显示拉萨市高中阶段大部分数学教师的试卷分析还处于前计算阶段。［7］试卷分析不等于教师把试卷从头到尾做一遍，更不等于教师完全凭借经验筛选出试卷讲评的重难点。科学的试卷分析是开展针对性、高效性讲评课的重要保障，转变试卷分析观念，重视试卷分析的深度与广度，能促进试卷讲评课效率。其中的广度可以通过扩大时间和空间维度、丰富样本量的方式实现；挖掘试卷分析的深度可以通过应用数据处理软件聚类和关联相关计算方法的方式达到，例如本研究中WEKA 平台下的Kmeans 算法和Apriori 算法，对教育数据进行深度分析，为此，需要对一线教师进行一定的教育测量和软件使用培训。

（三）学生填写试卷反思表

调查显示当前学生缺乏问题修正、反思和错题巩固的主观能动性。韦纳的归因理论认为正确的成败归因会提升学生自我效能感，激发学习动机，促进学业进步。因此，在学生自主性不足，还未养成自主反思的学习习惯前，教师争取每次测试后通过任务式或者督促式的训练方式让学生填写试卷反思表，提高学生成败归因、自我归纳和反思的技能，并通过教师针对性的指导，学生学会对成败（试题）正确归因。