考虑灵活性供需匹配的电力系统自适应时间尺度调度策略

李宏仲，叶翔宇

（上海电力大学电气工程学院，上海市 200090）

0 引言

随着“双碳”战略目标的提出，风电和光伏等可再生能源（RES）得到了迅速开发和利用。然而，高比例RES 的接入，增加了电力系统灵活性需求的不确定性，改变了原有的电力系统调度方式，这给新型电力系统维持电力电量平衡带来了挑战［1-4］。

针对上述问题，电力系统优化调度多采用灵活性资源优势互补的调度模式，满足新型电力系统的电力电量平衡［5］。文献［6］建立了水电和火电的联合调度模式，利用水电机组的灵活可控特性，平抑灵活性需求的快速波动。文献［7-8］考虑到储能设备具有能量双向流动和启动调节过程方便快速等优势，提出了利用抽水蓄能或者电池储能等设备满足系统灵活性需求。文献［9］建立了虚拟电池模型，将系统内多种灵活性资源进行聚合，调度过程以集群分配功率最优为目标，进而得到功率可调节域以应对不确定性影响。

但是高比例RES 接入后，系统的灵活性需求呈现非平稳性，在不同时间尺度上具有幅频特征的差异。可以根据灵活性需求的波动特征匹配与之吻合的灵活性资源，从而提高灵活性资源的利用效率。

目前，分析非平稳序列多采用信号分解技术。文献［10］采用小波包技术分解风电功率序列，根据充放电速度和响应周期划分储能类型。然后，确定与储能设备状态变化率相匹配的分解子模态序列。文献［11］采用形态学技术分解灵活性需求，根据可控设备的响应时间和幅度，确定不同时间尺度下的灵活性供需匹配集合，实现了灵活性资源的协同配合以及最大化利用。2014 年变分模态分解被提出后受到了广泛关注和应用［12］。文献［13］在微电网调度策略制定中，采用了变分模态分解处理光伏和负荷数据，根据调度单元的响应速度确定长、短时间尺度下的调度对象。后续可以在现有分解过程的基础上深入分析子模态瞬时频率均值的变化趋势特征，以瞬时频率均值的变化趋势出现大幅度降低作为确定分解层数的依据，避免主观确定分解层数影响结果精确度。

为了保障调度结果的可靠性，文献［14］提出了多级协调、逐级细化的调度模式。其中，多级协调主要表现为多时间尺度的相互配合，但是在新型电力系统中，传统1 h 或15 min 的固定时间尺度调度模式，可能使得波动较快的灵活性需求在调度过程中被湮没，因此，根据灵活性变化确定调度时间尺度具有一定的研究意义。文献［15］考虑到火电机组不易频繁调节的问题，利用复杂度分析方法确定净负荷序列中波动剧烈和平缓的时段。当波动过程剧烈时缩短时间尺度，反之则适当扩大时间尺度，避免了频繁调整火电机组的运行工况。本文根据分解后子模态的波动特征自适应确定该模态的调度时间尺度，更加全面地对调度时段进行划分。

另外，新型电力系统中不确定性进一步加大，基于预测值的确定性优化调度可信度不高，因此需要考虑到RES 出力不确定性场景问题。不确定性模型主要包含概率模型、模糊模型和区间模型等［16-17］。其中，区间模型具有建模简单，通过改变区间数即可描述其不确定性的优势。文献［18］采用了区间数描述了风电光伏的波动情况，并利用区间序关系等方法将区间优化转化为确定性优化模型。文献［19］采用区间变量表征RES 出力预测误差和需求侧响应的不确定性，计算对比不同置信水平下的调度结果，综合系统可靠性和经济性确定调度计划。

综上所述，本文在现有研究的基础上，提出了一种考虑灵活性供需幅频匹配的电力系统日前自适应时间尺度调度策略。该策略在计及RES 日前出力不确定性和波动性的基础上，利用分解技术得到具有不同波动特征的子模态序列，并根据子模态特征匹配灵活性资源、确定调度时间尺度和建立优化调度模型。同时，本文利用均值变化特征，改进了变分模态分解技术，提出了均值变分模态分解（MVMD），利用极限变化阈值定量判定是否出现过分解，从而合理地确定分解子模态的层数m。优化模型中增加了供需匹配结果的幅值约束，目标函数考虑了灵活性传输限制。最后，采用改进型IEEE 39 节点系统和实际省级电网数据开展算例分析，验证本文所提策略的可行性。

1 灵活性需求不确定性建模

在新型电力系统中，灵活性需求不但来自负荷，风电和光伏出力也存在不确定性和波动性，需要灵活性资源予以平衡和支撑。因此，可将两者合并，采用净负荷序列的变化趋势描述灵活性需求，如下所示。

1.1 区间不确定性模型

定义RES 日前出力预测误差率为实际值与预测值之差除以预测值。已知该预测误差率符合正态分布通过改变预测误差率的置信水平值，即可得到误差率的区间范围，进而得到不确定性场景S。假设选取n个置信水平，可得到由s1到sn的不确定性场景。每类场景的区间上下限值代表了该场景中的不确定性边界情况。

区间模型是使用区间范围表示可能发生的所有事件。存在界限范围的问题，均可采用区间数学方法解决。通用表达式如式（2）所示［21］。

1.2 区间潮流模型

利用区间潮流求解上述区间模型，计算各类不确定性场景下系统的节点电压等系统参数。将RES 接入点视为PQ节点，功率因数为φ。假设测试系统为N节点系统（nd=1，2，…，N）。RES 接入点功率平衡方程如式（6）至式（12）所示。

2 灵活性供需幅频特征分析

2.1 需求侧幅频特征分析

灵活性需求分析采用MVMD 技术在频域中进行分解。该技术本质是自适应最优Wiener 滤波器组，因此，可通过自动调整窗内局部方差来保证输出子模态具有相同时延。分解结果消除了原始序列的非平稳性。各类子模态序列反映了净负荷序列中所包含的波动特征。具体的计算式和瞬时频率均值求解过程详见文献［22］，本文不再赘述。

MVMD 利用瞬时频率均值明显变化这一特征确定分解层数。本文通过计算极限变化阈值对均值明显变化进行定量分析并提出一般性原则。假设采样周期为Y，通过计算可以得到原始序列中所包含的瞬时频率值f，如式（14）所示。

由上式可以确定瞬时频率中的最大值fmax和最小值fmin。假设在极限状态下，存在子模态序列中频谱成分均由最大或最小瞬时频率构成，那么该子模态的瞬时频率均值为fˉmax=fmax或fˉmin=fmin。因此，在未出现过分解问题时，瞬时频率均值的极限变化阈值Δf∞如式（15）所示。

设定净负荷功率序列的MVMD 预分解层数为K，定义子模态分量的幅值序列为(t)。确定分解层数的步骤如下。

1）计算原始序列中所包含的瞬时频率值，确定极限变化阈值Δf∞。设定预分解模态数为K。求解变分优化模型，得到模态数1 至K的子模态分量。

2）对子模态做希尔伯特变换，计算各模态的瞬时频率均 值fˉK。

3）按照模态分解顺序连接瞬时频率均值，计算不同分解层数下的均值变化情况。

4）当分解层数为m+1 时，出现m+1 层的瞬时频率变化值Δfm+1大于Δf∞时，说明此时分解个数过多，出现了信号断裂导致瞬时频率出现了零值。根据该特征，从预分解层数K中，选出最优分解层数m。

2.2 供给侧幅频特征分析

在新型电力系统中，灵活性资源主要包含具有调节能力的燃气机组、经灵活性改造的火电机组、各类储能设备和可中断负荷。由于火电机组的响应周期受到蒸汽压力、汽轮机的机械损耗、炉管热疲劳和爬坡能力等限制，该设备的灵活性调整能力较差，响应周期通常为小时级，并且为应对可再生能源的不确定性预留部分旋转备用［23］。燃气机组的灵活性较高，响应周期也比火电机组较短，响应出力模型如式（16）所示。

储能设备主要分为功率型和能量型，其出力模型如式（17）所示。功率型储能相较于能量型储能具有响应周期短的优势，但容量较小。能量型储能的成本较低，且响应容量大，但响应周期较长，因此，功率型储能和能量型储能通常组合使用，该模式具有较好的经济效益［24］。

本文可削减负荷主要是通过电网调度机构与参与者签订用电激励政策合同，保障用户侧给系统提供一定的灵活性供给，其出力值如式（18）所示。

另外，本节对上述灵活性资源的响应周期，采用模糊划分的方法进行了分析，具体如附录A 图A1所示［11］。

3 基于灵活性供需匹配的调度策略

3.1 灵活性供给和需求的幅频匹配

灵活性资源和需求的幅频匹配框架如图1 所示。具体过程主要包含灵活性需求的分解过程和子模态与灵活性资源的匹配过程。首先，采用MVMD方法分解原始需求序列，当模态分解层数为m时，各个模态对应的瞬时频率均值由低到高分别为fˉm，fˉm-1，…，fˉ1。将 子 模 态 瞬 时 频 率 均 值 作 为 灵 活 性 需求的波动周期。然后，采用模糊法分析灵活性资源的响应周期。最后，利用匹配度指标，求解每类灵活性资源与m个子模态的匹配程度。

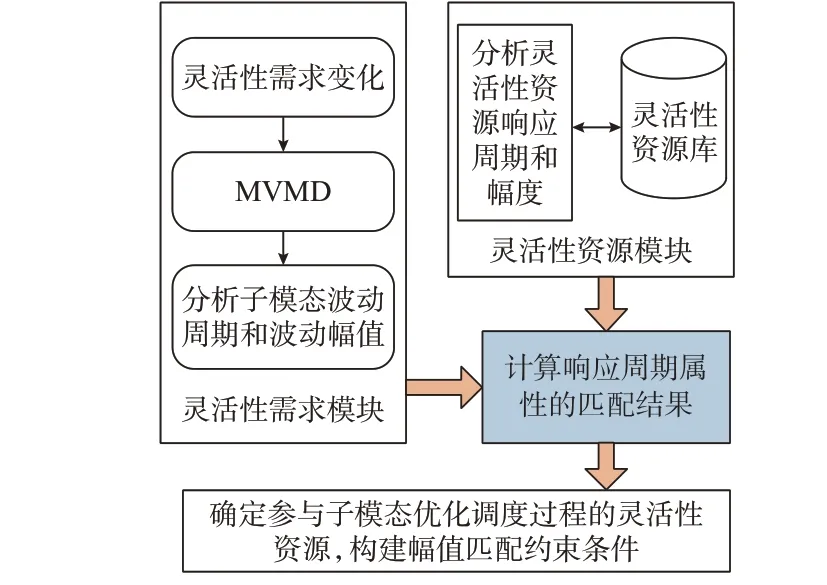
图1 供需幅频匹配框架Fig.1 Supply-demand amplitude-frequency matching framework

匹配框架内包含灵活性资源模块和灵活性需求模块。灵活性资源模块中包含响应周期属性和功率响应幅值属性。定义响应周期属性如式（19）所示。

式中：SR为灵活性资源的响应周期属性矩阵；S1至SZ分别为第1 至Z个灵活性资源的响应周期属性。

分解层数为m时，得到的子模态序列矩阵PELm，t如式（20）所示。灵活性需求模块中包含分解子模态序列的波动周期属性和波动幅值属性，周期属性如式（21）所示。

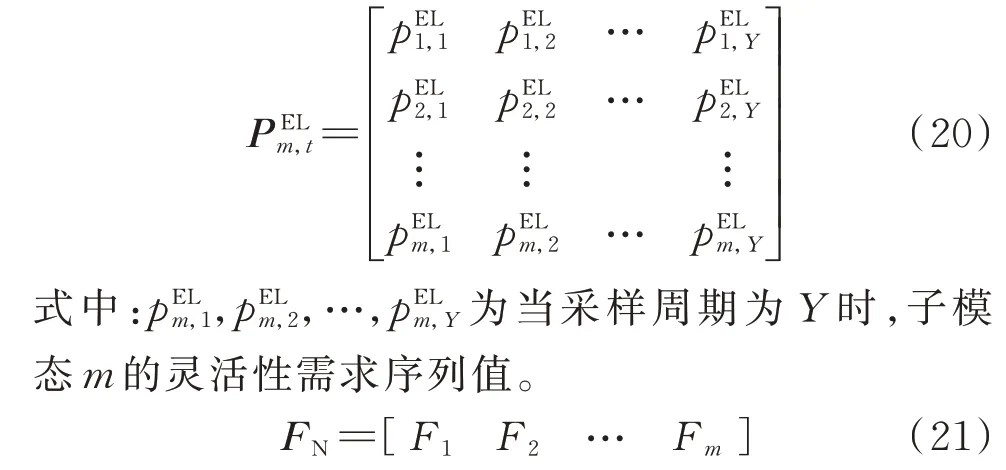
式中：FN为各类子模态的灵活性需求的波动周期属性矩阵；F1至Fm分别为第1～m个子模态的波动周期属性。

然后，根据灵活性资源的响应周期属性和灵活性需求的波动周期属性，建立特征匹配度指标，如式（22）所示。为计算所得每类匹配度指标组成的矩阵。该指标体现了每类灵活性资源的响应周期与各类灵活性需求子模态的匹配程度。

式中：Qp为灵活性资源的速度属性与需求中的波动周期属性的特征匹配度指标矩阵，矩阵中的数值体现了每类灵活性资源的响应周期与各类灵活性需求子模态的匹配程度；A1和A2为矩阵变化的辅助矩阵。

对于Qp中存在大于0 的匹配度指标时，说明该指标对应的灵活性资源的响应周期小于灵活性需求的波动周期。此时，灵活性资源能够满足跟踪灵活性变化的能力。对于Qp中小于0 的指标，灵活性资源和需求的频谱不匹配，对应的资源不参与该子模态的调度过程。

考虑到电力系统灵活性供给和需求匹配过程中存在不平衡的问题，本文采用了弃风弃光及切负荷的手段改变原灵活性需求时序特征。对于电力系统而言，功率平衡表征了灵活性供需之间达到了平衡。因此，可通过功率是否平衡，描述在不同时刻灵活性需求和灵活性供给之间是否存在不平衡的关系，进而确定是否需要调用弃风弃光及切负荷来满足灵活性需求。定义σqc为弃风弃光及切负荷的行为因子，有

当σqc=1 说明了原序列中存在灵活性需求大于灵活性供给的情况，需要调用弃风弃光及切负荷的功率。反之，当σqc=0 说明灵活性供需平衡，弃风弃光及切负荷不参与调度过程。

最后，根据频谱匹配结果建立考虑灵活性供需之间不平衡情况下的幅值约束条件，包含子模态的功率平衡约束和设备的出力约束。其中，子模态功率平衡约束中的弃风弃光和切负荷量如式（26）所示。将约束条件增加至优化模型的求解过程中：式（27）表示在t时刻，子模态所匹配的灵活性资源出力值要满足对应模态功率需求；式（28）至式（32）表示灵活性资源在每类模态中的总出力值要介于出力上下限内。

3.2 自适应时间尺度的优化调度

3.2.1 优化调度框架

根据不同灵活性供需的幅频匹配结果，建立自适应时间尺度组合的调度模型，如图2 所示。

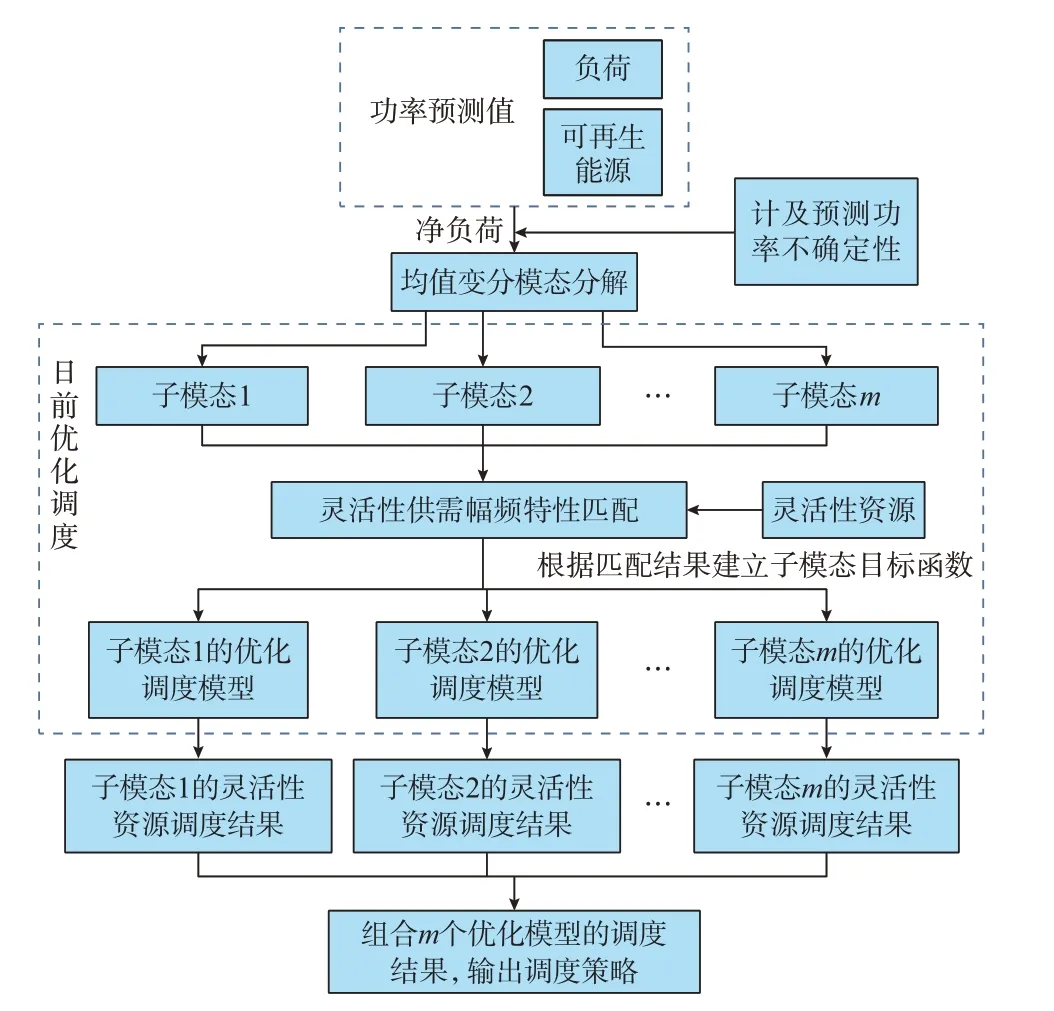
图2 优化调度策略框架Fig.2 Optimal dispatching strategy framework

子模态调度时间尺度的选取考虑了波动周期和计算过程。利用子模态瞬时频率均值计算对应的变化周期τψ，将τψ按照式（33）进行优化得到模态ψ的调度时间尺度。

式中：τψ为变化周期的计算值；为子模态对应的实际调度时间尺度；N*表示正整数集。

3.2.2 优化目标函数

计及灵活性传输限制可能造成线路堵塞的问题，本文将超出线路安全边界的部分功率认定为造成了网络堵塞。建立线路灵活性传输限制惩罚成本，对造成灵活性传输限制的部分进行惩罚。针对灵活性供需之间不平衡的时序特征，采用了弃风弃光及切负荷惩罚成本。在调度过程中，当系统资源无法满足灵活性需求时，将由惩罚环节提供相应的灵活性。

系统运行成本为灵活性资源的出力成本、设备维护成本、运行成本、灵活性传输限制惩罚成本和弃风弃光以及切负荷惩罚成本。本文假设储能电站的投资者为电力系统运行方，主要考虑储能补贴收益和低储高发收益。具体目标函数如下。

1）灵活性传输限制惩罚成本

定义线路的堵塞系数D，以判断线路是否发生堵塞。

式中：Pl，t为t时刻在线路l上流过的功率；Pl，max、Pl，min分别为线路容量上、下限；D＞0 时，表示线路无堵塞，D≤0 时，表示线路发生堵塞，且D数值越大，表示堵塞情况越严重。

根据堵塞系数确定是否考虑堵塞惩罚成本，当D≤0 时，行为因子σ取值1，相反则取值0。惩罚目标函数如式（36）所示。

式中：αi、βi和γi为第i个火电机组 对应的出力成本系数；CON为启机爬坡成本系数；COFF为火电机组的关机成本系数；σi，t为t时刻第i个火电机组的行为因子；CPA为爬坡成本；PH，i，t为第i个火电机组在t时刻的出力值。

3）燃气轮机运行成本

燃气轮机的运行成本CMT包含出力成本和维护成本，其中出力成本考虑了燃气转换效率ηg，有

5）弃风弃光和切负荷惩罚成本

式中：Cqc为弃风弃光和切负荷惩罚成本；CWPqc为弃风 弃 光 成 本；CLqc为 切 负 荷 成 本；cWPqc，t、cLqc，t分 别 为时刻t弃风弃光单位惩罚成本和切负荷单位惩罚成本；PWPqc，t和PLqc，t分 别 为t时 刻 的 弃 风 弃 光 量 和 切 负荷量。

3.2.3 优化调度约束条件

优化调度过程需要满足系统运行约束、能量平衡约束和各类设备出力的不等式约束等。等式约束包括潮流等式约束、储能始末状态约束、可转移负荷移入和移出约束。不等式约束主要包括节点电压、线路电流、资源的出力和爬坡约束等。

弃风弃光和切负荷的约束条件参见文献［26］。潮流约束中的二次项可转化为二阶锥问题。除此之外，灵活性供需幅频匹配的幅值约束如式（26）至式（32）所示。设备的运行约束如式（16）至式（18）和式（45）至式（47）所示。储能设备包含充放电约束和荷电状态约束，荷电状态要满足初始时刻和结束时刻状态相同。

4 算例分析

4.1 算例参数设置

在原IEEE 39 节点测试系统中增添4 座风力发电站，容量依次为400、300、200、100 MW；增加2 座光伏发电站，容量均为300 MW；保留5 台燃煤机组，新增3 台燃气轮机并网，单机容量为150 MW。优化后的系统如附录A 图A2 所示。负荷和可再生能源出力预测值参考文献［27］，出力时间间隔为1 min，如附录A 图A3 所示。

储能设备和可再生能源电站配合使用，考虑储能设备的特征互补和组合运行成本［22］，储能电站分别采用规格为20 MW/3.35 MW·h 的超级电容器和80 MW/80 MW·h 蓄电池组合配置。所有储能的初始荷电状态为0.35。设备参数见附录B 表B1，负荷参与调度的激励成本见附录B 表B2，负荷根据事先计划安排参与调度工作，调度时间不得少于1 h。灵活性限制惩罚为300 元/（MW·h）。采用MATLAB下Yalmip 工具箱调用CPLEX 求解器进行求解，为了提高求解效率，求解过程中修改默认收敛间隙MIPGap，设置为0.05［28］。同时，采用内存为128 GB，处理器为Intel Xeon CPU E5-2670 的计算机进行求解，避免了维数过大导致的求解效率较低的问题。

4.2 MVMD 方法分解结果分析

采用MVMD 方法分解净负荷序列，分解过程考虑到了原始数据采样频率和分解程序中信号频率设置的一致性问题。其瞬时频率均值变化趋势特征如附录A 图A4 所示。

已知原始序列中极限变化阈值Δf∞为0.001 03 Hz。当分解子模态数为3 时，变化阈值Δf3为0.000 943 Hz，小于极限变化阈值。当分解子模态数为4 时，变化阈值Δf4为0.001 18 Hz，大于极限值。因此，选取m=3 为最优分解数。按由小到大的顺序排列，fˉ1=0.000 081 9 Hz、fˉ2=0.000 232 Hz、fˉ3=0.001 025 Hz。净负荷序列的分解结果如图3所示。

图3 净负荷分解结果Fig.3 Decomposition results of net load

由分解结果，可以得到灵活性需求模块中的波动周期属性和波动幅度属性。

4.3 调度结果对比分析

4.3.1 灵活性供需匹配度计算

根据算例中灵活性资源的响应周期以及分解子模态的变化周期，计算与子模态1、子模态2 和子模态3 相匹配的灵活性资源。计算结果如附录A 图A5 所示。由图A5 可以看出，对于子模态1 而言，波动周期较长，因此，所有灵活性资源均可以响应该模态的灵活性需求。由于燃煤机组的响应周期为小时级，两者的匹配度最高。因为燃气轮机的响应周期相较于燃煤机组较短，所以可以响应变化较为频繁的灵活性需求序列。除此之外，超级电容器的响应周期是所有灵活性资源中最快的，能够响应波动周期最短的灵活性需求。对于响应周期较长的灵活性资源则无法满足波动频繁的子模态，其匹配度为负值。

4.3.2 不同场景下的调度结果对比

根据4.2 节中瞬时频率均值的大小，可以自适应地计算得到每个子模态的变化周期为τ1=3.39 h、τ2=1.19 h 和τ3=0.27 h。通过式（33）得到优化后的3 个子模态集合的调度时间尺度分别为τ*1=3.00 h、τ*2=1.00 h 和τ*3=0.25 h。

为验证本文所提方法的合理性和经济性，本节设置两种调度场景作为对比项。

场景1：不考虑幅频特征匹配，以可再生能源出力和负荷数据为基础，以成本最优为目标，成本中不计及灵活性传输限制惩罚，调度时间间隔取固定1 h。

场景2：考虑幅频特征匹配，按照匹配结果和波动周期，建立自适应时间尺度的调度模型并据此进行求解，计及灵活性传输限制惩罚成本。

附录A 图A6 和图A7 分别为场景1 和场景2 的调度结果。可以看出，在08：00 时和20：00—21：00时的负荷高峰时段和15：00 时的负荷低峰时段，均有可削减负荷动作来满足功率平衡。燃煤机组由于响应周期较长，因此，其追踪灵活性需求变化的能力较差。灵活性资源中，燃气轮机的输出功率较大，并且响应周期也较短，因此在两个场景中均发挥了重要作用。但是由于场景2 中燃气轮机与子模态2 的相关性较强，其主要满足该模态的灵活性需求。通过灵活性供需之间的匹配结果建立调度模型有利于储能的合理利用。蓄电池电站为长时间尺度调度单元，在净负荷低谷时期持续充电，在高峰时段平稳放电。其余储能设备能够实现迅速充放电，快速跟踪净负荷的高频波动。

1）经济性和计算效率对比

对比场景1 和场景2 的优化调度计算效率和经济性，结果如附录B 表B3 所示。可以看出，按照灵活性供需幅频匹配结果进行计算具有高效性。虽然高频子模态的时间尺度较短，但与之匹配的灵活性资源较少，计算复杂度降低。自适应时间尺度的调度模式，增强了灵活性资源追踪灵活性变化的能力。同时，系统受制于网络安全运行约束，灵活性传输限制惩罚成本相对较小。本文所提策略能够在保证灵活供给的情况下，有效地减少弃风弃光及切负荷，提高系统运行经济性。总体而言，相较于场景1而言，场景2 的调度效率提升了4.98%，调度成本降低了3.90%。

2）燃煤机组追踪效果对比

附录A 图A8 和图A9 分别为场景1 和场景2 中燃煤机组的出力结果。可以看出，场景1 中燃煤机组在08：00—10：00 时、13：00—15：00 时和19：00—20：00 时均出现机组短时1 h 级的功率调整，并且机组的出力变化基本在所有调度时段均有体现。但在场景2 中，燃煤机组所匹配的灵活性需求为子模态1，其自适应调度时段为3 h，在调度时段内燃煤机组保持稳定运行，不会出现变出力的情况。对比场景1 和场景2 中的燃煤机组的爬坡成本如表1 所示。

表1 燃煤机组出力结果对比Table 1 Comparison of output results of coal-fired units

由结果可以看出，场景2 的爬坡成本比场景1降低了56.5%，上爬坡总量和下爬坡总量也分别减少了47.8%和65.8%。

3）灵活性需求追踪效果对比

由于子模态1 所匹配的燃煤机组的出力稳定性，为了满足功率的实时平衡，需要灵活性资源进行补充。场景1 和场景2 的灵活性资源出力结果对比如附录A 图A10 所示。

通过分析场景1 和场景2 中超级电容器的灵活性追踪能力以及蓄电池储能和燃气轮机的响应功率，验证本文所提策略的优势。可以看出，在场景2调度模式下，超级电容器与子模态3 匹配度最高，并且子模态3 的灵活性需求变化快速，因此该资源的总出力值基本根据灵活性需求的变化而变化，在04：00 时和11：00 时对灵活性的突然变化均具有很好的跟踪能力。而场景1 的调度计划不具备针对性。燃气轮机主要是响应子模态2 的变化过程，同时作为子模态1 的补充资源，因此相较于场景1 而言整体出力较为平稳。但在10：00—12：00 和18：00—21：00 时存在出力波动现象。其中，场景2 的上爬坡量比场景1 降低了22.3%，下爬坡量降低了21.9%。场景2 中，考虑幅频匹配以及自适应时间尺度后，燃煤机组需要有更多资源与其配合。由于蓄电池与子模态1 的匹配度较高，增强了蓄电池对灵活性需求的响应能力，响应功率比场景1 提高了31.6%。

4.4 不同区间数的调度结果分析

为解决RES 出力预测的不确定性问题，根据不同置信水平下的预测误差率得到灵活性需求区间，如附录A 图A11 所示。从图中可以看出，当置信水平为98%时基本涵盖了所有可能发生的状况，但若按此进行配置容易导致配置冗余性较高。对灵活性资源和需求进行幅频匹配，并对每种置信水平求解区间最优潮流，得到灵活性资源的最优出力计划。

表2 为不同置信水平下，灵活性资源的出力区间值。由表中数据可以看出，燃煤机组在不同置信水平的调度方案中都保持在较高的水平。随着置信水平的降低，燃气轮机的出力上限也在降低，系统预留灵活性供给也相应减少。因此，实际工程中综合天气变化状况、负荷变化状况和经济性等因素，选择合适的置信水平指定调度计划。

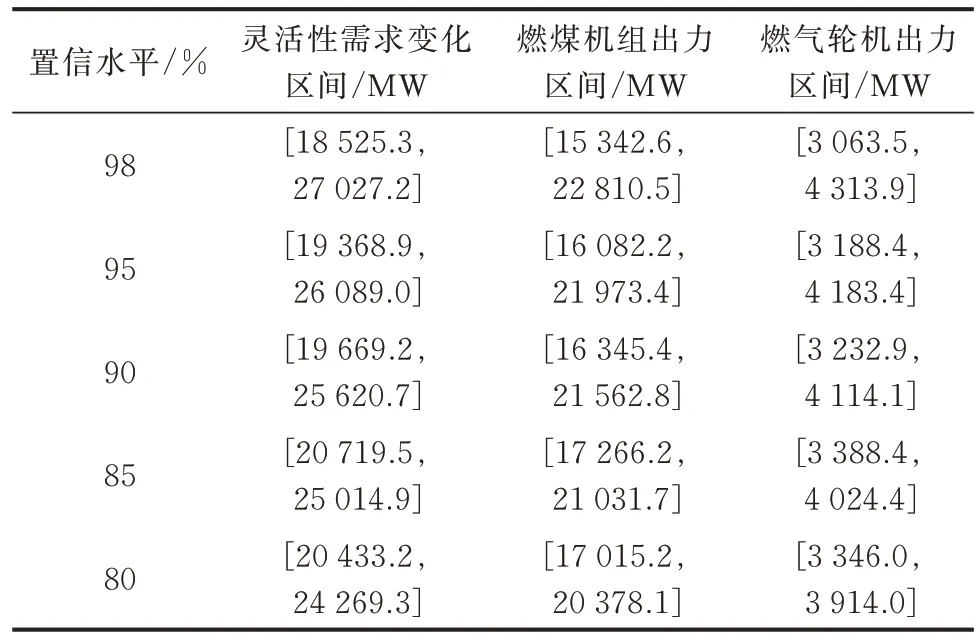
表2 不同置信水平最优出力区间Table 2 Optimal output interval with different confidence levels

4.5 省级电网算例分析

为了充分体现该调度策略的优势，本文基于中国南方某省级电网实际运行方式和部分运行数据，开展了实例分析。其中，省级电网燃煤机组装机容量见附录B 表B4，出力成本系数参见文献［29］。已知该省燃煤机组总装机容量为65 155 MW，其中风电场装机容量为3 480 MW，光伏电站装机容量为3 740 MW，灵活性资源包含燃煤机组、快速调节的燃气机组、可调节水电站和储能电站［10］。

由2.1 节的分解原理可以得到典型日灵活性需求的原始曲线以及分解结果，见附录A 图A12。其中，子模态1 的瞬时频率均值为0.000 032 5 Hz，子模态2 的瞬时频率均值为0.000 129 Hz。

4.5.1 灵活性供需匹配度计算

根据省级电网中灵活性资源的响应周期以及分解子模态的变化周期，计算与子模态1 和子模态2相匹配的灵活性资源。计算结果如附录A 图A13所示。可以看出，子模态1 的波动较为平缓，波动周期较长，所有资源均与之匹配。但由于火电机组和储能电站中的能量型储能的响应周期较长，两类灵活性资源和该模态的匹配度较高。对于波动周期较短的子模态2，快速调节的燃气机组和功率型储能与之具有较高的匹配度。另外，可调节水电站也可作为子模态1 和子模态2 的辅助资源，以防止灵活性不足或灵活性堵塞等问题。

4.5.2 不同场景下的调度结果及其对比

根据4.2 节中瞬时频率均值的大小，可以自适应地计算得到每个子模态的变化周期为τs1=8.54 h和τs2=2.17 h。通过式（33）得到优化后的2 个子模态集合的调度时间尺度分别为τs*1=8.00 h 和τs*2=2.00 h。

场景设定与上文相同，场景1 为不考虑幅频特征匹配，以成本最优为目标，调度时间尺度为固定的1 h。场景2 则考虑了幅频特征匹配，按照匹配结果和波动周期，建立以成本最优为目标的自适应时间尺度调度模型。基于省级电网运行数据的两种场景调度结果如附录A 图A14 和图A15 所示。由于场景2 中子模态1 具有幅值高且波动平缓的特征，燃煤机组承担了较大的灵活性需求。而燃气机组和可调节水电站与子模态2 的匹配度较高，所以场景2中燃气机组出力总量相比于场景1 的降低了1.84%，可调节水电站的出力总量相较于场景1 降低了19.09%，同时也降低了设备运行工况变化次数。

附录A 图A16 和图A17 为场景1 和场景2 中燃煤机组的出力对比。可以看出，场景2 中根据子模态的波动确定调度时间尺度的调度策略有利于维持燃煤机组输出恒功率。能量型和功率型储能也与之配合，总储存和释放能量相较于场景1 提高了16.86%。

表3 为燃煤机组出力结果对比，自适应时间尺度的调度策略降低了机组的爬坡总量，场景2 中的上、下爬坡总量比场景1 降低了34.70%和15.95%。爬坡成本降低了29.51%，燃煤机组的出力成本降低了0.41%。

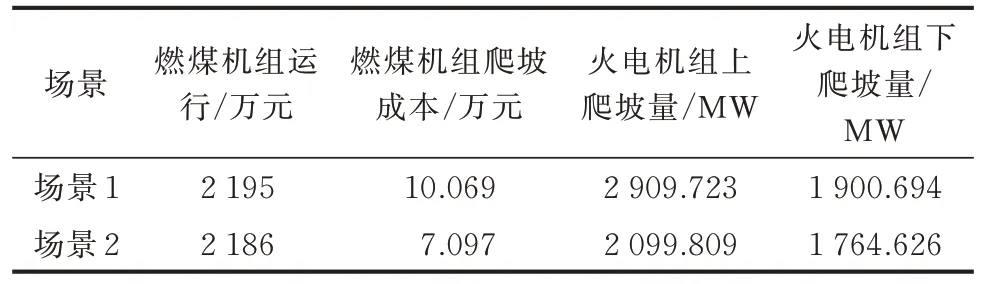
表3 省级燃煤机组出力结果对比Table 3 Comparison of output results of provincial coal-fired unit

5 结语

本文提出了一种考虑灵活性供需幅频匹配的电力系统日前自适应时间尺度优化调度策略。该策略首先采用区间法分析了RES 出力不确定性，其次提出极限变化阈值判断均值变分模态是否过分解，然后搭建灵活性供需特征匹配框架。依据匹配结果建立调度模型，并根据需求波动自适应确定调度计算时间。最后，根据算例结果，得出了如下两方面的优势。

1）灵活性供需匹配以及子模态之间并行计算，实现了灵活性资源的充分利用，显著提升了调度经济性。自适应调度时间尺度，提高了对高频灵活性波动的追踪能力，调动了灵活性资源积极性，解决了固定调度时间对快速波动的湮灭问题，避免了RES接入导致的燃煤机组频繁改变运行工况的情况，有利于长时间尺度的稳定运行。

2）考虑RES 出力预测不确定的调度方案，能够有效避免实际调度过程中功率平衡不满足导致的系统安全问题。区间分析法为系统的运行和设备的出力均制定合理区间，保证了系统方案符合工程需求。

本文的调度策略着重分析了源荷灵活性匹配，对电力系统网络灵活性分析仅局限于考虑了网络堵塞对于灵活性的影响。后续，应进一步对网络提供灵活性方面展开研究，并将网络加入灵活性匹配过程中，形成源网荷灵活性整体协同。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。