新能源电力系统灵活性供需量化及分布鲁棒优化调度

童宇轩，胡俊杰，刘雪涛，陈 璨，马 原

（1.新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2.华北电力科学研究院有限责任公司，北京市 100045）

0 引言

可再生能源发电设备和并网技术快速发展，以新能源为主导的新型电力系统逐步形成［1-2］。高比例新能源的随机波动性导致电力系统的运行调度难度显著增加，传统灵活性资源如常规机组的灵活性供给能力已难以有效满足系统剧增的灵活性需求。与此同时，电网在局部时段灵活性严重不足的现状，使得需求侧灵活性逐渐成为电网调度运行的研究核心。

国 际 能 源 署（International Energy Agency，IEA）将灵活性定义为：在一定时间尺度下，电网中灵活性资源满足灵活性需求的能力［3-4］。灵活性需求的量化是进行灵活性供需平衡分析的关键。目前已有文献对灵活性需求的量化方法展开了研究［5-7］，但均未考虑不确定性因素。文献［8-10］采用联合概率分布函数描述净负荷的随机性。这一类基于概率的方法无法准确给出电力系统各时段的灵活性需求与调节能力，且受限于不确定量的概率分布情况。文献［11］在预测值的基础上用误差系数表征灵活性需求的不确定性波动范围，处理过于简单。

近年来，鲁棒优化（RO）和随机优化（SO）被运用到不确定性因素影响下的灵活性供需平衡研究中。文献［12-13］通过鲁棒与条件风险价值构建灵活性供需平衡的运行域。文献［14-15］通过多场景法求解灵活性裕度，并根据Bernstein 多项式理论确定基准值，建立了综合随机优化模型。上述方法在灵活性供需的刻画上均存在过于保守或冒险的问题 。分 布 鲁 棒 优 化（distributionally robust optimization，DRO）模型结合了两者的优点，使用不确定概率密度描述不确定性，从而寻找最恶劣场景下的概率分布。传统DRO 基于矩信息或KL（Kullback-Leibler）离散度等距离量构建概率分布模糊集合进行优化［16］。前者通常为难以求解的非确定性多项式（NP）难问题，需要预先明确不确定量的分布类型，且样本数据较多时过于保守；后者当假设误差较大时，概率模糊集有失去意义的风险。基于此，一种基于数据驱动的DRO 得到了重视［17］。该模型通过提取电力系统运行的大量历史数据样本，建立综合范数不确定概率集合表征不确定性。通过历史数据而不是表征整体性能的矩信息指导决策，对样本数据进行了充分利用，具有求解简单、经济灵活性好的优势［18］。目前数据驱动的DRO 已初步运用在选址定容［19］、机组组合［20］等领域，但在灵活性供需优化调度中尚无研究报道。

需求侧资源可以在运行充裕性和经济性上代替发电侧提供灵活性平衡［21］。然而，前文所述研究均忽视了需求侧资源所能提供的灵活性供给能力，对于需求侧资源参与电力系统优化调度的研究侧重点目前仍在“电力平衡”。该问题属于电力供需的静态过程，忽略了一定时间尺度上的供需波动特征，无法充分激发需求侧灵活性资源的调节潜力。随着电力系统运行方式从传统电源匹配负荷的单向模式转换为源-网-荷-储协调互动的双向模式，电网调度需要通过调动各类需求侧资源实现“灵活性平衡”，满足各个时段的灵活性爬坡需求［22-23］。

此外，已有供需灵活性研究鲜有考虑风光出力的相关性，且传统相关性分析方法难以有效体现新能源出力之间的互补特性，造成出力集合描述的不准确［24］。基于上述问题，本文建立了考虑灵活性供需平衡的数据驱动分布鲁棒优化调度模型，主要创新点如下：1）运用Copula 理论构建风光时空相关性出力集，并结合场景法与区间法对灵活性需求进行量化；2）考虑电动汽车等需求侧资源的灵活性供给能力，通过比较多种灵活性调节方式验证了模型的有效性；3）提出的数据驱动DRO 模型可以有效控制电网调度灵活性与经济性的鲁棒程度，并通过与现有不确定性算法比较验证了模型的优越性。

1 电力系统供需灵活性与量化模型

电力系统灵活性作为充裕性的补充［25］，研究的是一定时间尺度下电力功率的波动问题。源荷的双重波动需要调用灵活性资源匹配，若系统的灵活性不足就会存在弃风和切负荷的风险。

对电力系统的灵活性进行量化需要分别确定灵活性需求和灵活性资源的灵活性供给能力。考虑灵活性的时间尺度特性、方向性以及状态相依性，依次从灵活性需求、灵活性供给、灵活性平衡进行说明。

1.1 考虑时空相关性与不确定性的灵活性需求量化

由于风光具有反调峰特性，电力系统净负荷曲线呈现出典型的“鸭嘴”形状。负荷在早高峰过后快速下降，午后逐渐下凹，晚上由于用电高峰又迅速上升。随着新能源渗透率的不断提升，鸭嘴特性越发明显，如图1 所示。电网灵活性需求剧增反映出的调峰与爬坡困难将会导致灵活性出现缺额。

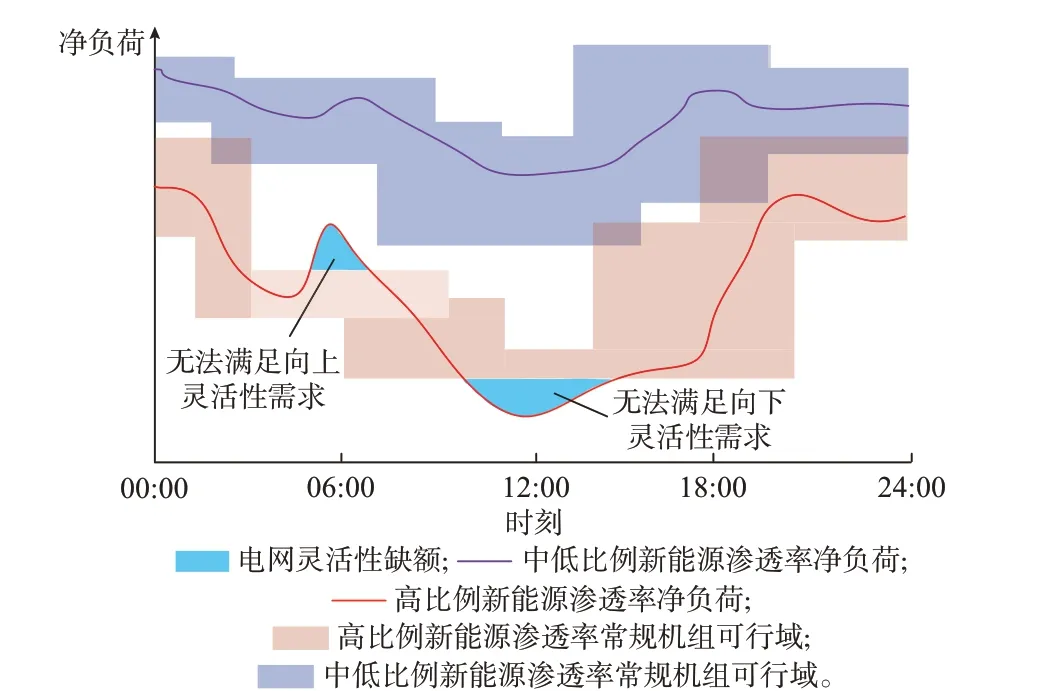
图1 高新能源渗透率下的“鸭嘴形”净负荷曲线Fig.1 “Duckbilled”net load curve under high penetration rate of renewable energy

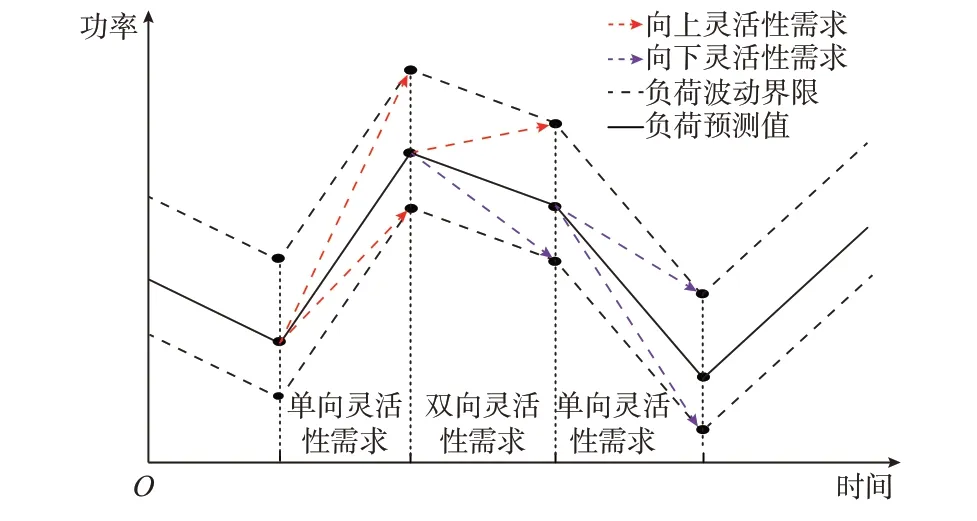
图2 灵活性需求量化示意图Fig.2 Quantification diagram of flexibility demands

1.1.1 基于Copula 理论的风光出力集生成

Copula 理论指出联合概率分布函数可以分解为边缘分布函数和Copula 函数的乘积。相比于传统简单的线性相关性分析，Copula 理论可以描述不同随机变量之间复杂的、非线性的相关性。Copula函数的选取关系到风光出力集合的准确性，考虑到风光出力之间具有互补特性，选用Frank-Copula 函数进行描述［26］。基于Copula 理论的风光时空相关性出力集生成原理详见附录A，具体步骤如下。

1）基于风光历史样本数据求各时段风电出力概率密度fW，t(xW，t)、分布函数FW，t(xW，t)，以及光伏出力概率密度fPV，t(xPV，t)、分布函数FPV，t(xPV，t)。

2）构建Copula 函数得到各时段风光出力联合概率分布H(xPV，xW)，生成一组具有时空相关性的风光变量边缘分布函数随机值{uPV，t，uW，t}。

1.1.2 灵活性需求量化

电网的灵活性需求来自风光负荷综合得到的净负荷的随机波动性。在数据驱动DRO 中，结合场景法与区间法对电力系统灵活性需求进行量化，从而在保证日前阶段灵活运行的同时降低保守性。本文采用基于概率距离的场景削减技术，从风光负荷样本数据中获得典型场景，详细步骤见附录B。以负荷为例，对于第k个场景考虑最大波动误差的负荷模型可表示为：

风电和光伏产生的灵活性需求量化过程与负荷类似，但是需要注意，作为电源其向下波动实际上产生向上灵活性需求，如式（3）和式（4）所示。

1.2 灵活性资源及灵活性供给能力分析

现有文献对电源侧参与灵活性供需平衡研究较多，忽视了需求侧的灵活性供给能力。本节将火电机组与抽水蓄能电站作为电源侧传统灵活性资源，常规固定负荷可通过负荷转移提供部分灵活性。电动汽车作为一种时耦资源，灵活性受到相邻时段可调功率与容量的限制，需要区别于普通负荷进行建模与分析。

1.2.1 常规机组

电力系统中的常规机组以火电机组为主，火电机组虽然总装机容量大，但是其爬坡速率低且受限于调度指令，故调节能力较差，只能提供有限的灵活性。灵活性供给可表示为：

1.2.2 抽水蓄能电站

抽水蓄能电站运行方式灵活，在多个时间尺度都具有良好的双向灵活性供给能力，可以为常规机组分担调峰需求。其灵活性供给受到时间尺度和水库蓄能的影响，可表示为：

1.2.3 常规可转移负荷

可转移负荷在电网调度过程中具有一定的灵活性，居民可以根据激励措施适当改变用电计划，提供双向灵活性供给［7］，可表示为：

1.2.4 集群电动汽车

电动汽车具有容量小、规模大的特点，只有通过电动汽车聚合商作为整体参与优化调度才能发挥灵活性。集群电动汽车响应时间迅速，可提供大量的双向灵活性供给。其供给能力主要受充电桩功率与车主出行习惯约束，可表示为：

当电动汽车聚合商集中控制的电动汽车数量较大时，若对每一辆电动汽车精确建模会使得优化求解陷入“维数灾“，所以本文使用文献［21］中基于虚拟电池（VB）模型的方法对集群电动汽车的灵活性进行刻画，建模过程详见附录C。

1.3 灵活性平衡

电力系统的灵活性平衡，即灵活性资源总的灵活性供给满足净负荷灵活性需求的能力。对各类资源灵活性供给能力进行整合，可以得到：

当裕度小于0 的时候，就会产生灵活性缺额，即：

需要注意的是，灵活性资源的灵活性供给包含了爬坡容量及备用容量，所以灵活性资源可以提供的容量备用属于灵活性容量。

1.4 功率平衡

各时刻需满足功率平衡约束：

灵活性资源其余常规约束详见附录C。

2 基于数据驱动的DRO 模型

2.1 确定性模型

本文通过引入灵活性缺额惩罚量化灵活性，构建以电网总运行成本最低为目标函数的灵活调度模型。不考虑新能源与负荷不确定性的目标函数为：

式中：F1为运行成本；F2为灵活性缺额惩罚成本。根据新能源优先上网政策，本文假设风光全部消纳，不参与电网优化调度。

电网运行成本包括火电机组煤耗成本、抽水蓄能调峰成本、可转移负荷补偿成本，以及集群电动汽车放电损耗补偿成本。

电力系统灵活性裕度不足时将会受到惩罚，灵活性缺额惩罚成本表示为向上灵活性缺额惩罚成本与向下灵活性缺额惩罚成本之和，如式（28）所示。

式中：Cdefc，t为时刻t处电网的灵活性缺额惩罚成本；Kdefc为灵活性缺额惩罚因子。

2.2 两阶段DRO 模型

为了寻找最恶劣场景概率分布下的最优灵活调度方案，本节基于负荷和新能源的历史样本数据，建立数据驱动的DRO 模型。本文涉及的DRO 是一个min-max-min 的两阶段3 层优化问题。第1 阶段min问题以电源侧各灵活性单元出力为决策变量，实现经济运行目标最优。第2 阶段max-min 问题寻找使得需求侧资源调用成本和电网灵活性缺额惩罚成本最小值最大的最恶劣场景概率分布，表达式如下：

式中：x为第1 阶段变量；y为第2 阶段变量；K为离散场景个数；pk为第k个场景出现的概率；r(x，ξk)为内层最小值问题的目标函数值；ξk为第k个场景；yk为第k个场景下的第2 阶段变量；f1为电源侧各单元出力成本；f2为需求侧资源调用成本和电网灵活性缺额惩罚成本；Ω为综合范数模糊集；U(x，ξk)为给定一组(x，ξk)时优化变量yk的可行域；h(x)≤0 为只与第1 阶段有关的约束，不考虑新能源与负荷场景概率的不确定性，为确定性约束；g(x，pk，yk)≤0为第2 阶段约束。

由于负荷与新能源的不确定概率集合难以获取，本文采用数据驱动的方法，在历史数据的M个样本中通过基于概率的削减方法得到K个离散的典型场景(ξ1，ξ2，…，ξK)表征不确定信息的可能值，并将此概率分布作为初始概率分布。考虑到各削减场景的离散值依然具有不确定性，为了保证场景概率的取值在合理范围内波动，构建以上述初始概率分布为中心的综合范数约束对不确定场景的概率分布进行限制，使其更接近真实场景。综合范数约束包含1-范数和∞-范数，分别如式（34）和式（35）所示。构建的综合范数模糊集如式（36）所示。

令式（37）和式（38）右边分别为不确定性概率置信水平α1和α∞，则在置信水平95%下，式（37）和式（38）保证了至少有95%可能性在给定集合内存在模糊分布［27］。θ∞和θ1可由式（39）进行计算。

偏差值θ∞和θ1表示DRO 的场景概率可以偏离初始场景概率的最大值，其值越大，鲁棒模型越保守，反之则越冒险。

3 两阶段模型求解算法

两阶段分布鲁棒优化通常基于零和博弈的思想，采用列与约束生成（C&CG）算法或割平面（Benders）算法求解，将原问题解耦成主问题和子问题进行迭代。相比于Benders 算法，C&CG 算法在求解主问题的过程中不断引入与子问题相关的辅助变量和约束，加快了收敛速度。

对两阶段模型（即式（29）至式（31））进行分解，得到主问题（MP）为：

子问题的目的是寻找使得需求侧资源调用成本和电网灵活性缺额惩罚成本最小值最大的最恶劣场景概率分布，当第1 阶段变量给定后，子问题可表示为：

式中：x*为主问题的解，这里为已知量。

子问题的形式虽然为一个NP 难的max-min 双层优化问题，但不难发现在各场景下内层的min 问题是相互独立的，可以采用并行计算的方法同时求解内层min 问题。因此，子问题可改写为两个单层优化问题依次求解，如式（42）所示。

式（42）为混合整数规划，可以使用Gurobi 求解器进行快速求解。求解得到的结果{pk}即为最恶劣场景概率分布，传递给主问题后进行迭代计算。

本文所提考虑电力系统灵活性供需平衡的数据驱动的DRO 模型求解流程如图3 所示。

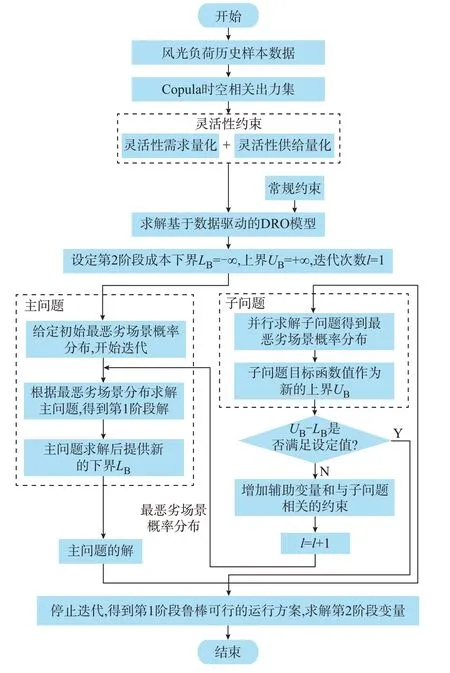
图3 数据驱动的DRO 模型求解流程图Fig.3 Flow chart for solving data-driven DRO model

4 算例分析

通过MATLAB 2016b 平台和Gurobi 求解器对算例进行求解。文献［19］建议研究日前电力系统灵活性的时间尺度τ为1 h，所以本文中日前灵活调度的时间尺度取为1 h。风光负荷数据样本在预测数值的基础上采用正态分布随机生成，样本数取500，通过基于概率距离的场景削减技术获得初始场景的概率分布，削减后场景数为5，典型场景曲线见附录D。日前负荷、风电、光伏最大波动系数εL、εW、εPV分别取0.05、0.10、0.08。算例各单元参数见附录E。

4.1 电力系统灵活性平衡结果

本节设定4 种灵活性调节方案，分析日前调度阶段负荷侧资源参与灵活性供给与加入灵活性平衡约束对电力系统灵活性裕度的影响。

方案1：负荷侧资源不参与需求响应（可转移负荷视为固定负荷，电动汽车无序充电），不考虑灵活性平衡约束。

方案2：负荷侧资源参与需求响应（电动汽车有序充放电），不考虑灵活性平衡约束。

方案3：负荷侧资源参与需求响应，考虑灵活性平衡约束。

方案4：负荷侧资源不参与需求响应，考虑灵活性平衡约束。

各方案电网的灵活性裕度及分析见附录F。由于方案1 和2 不考虑灵活性约束，优化调度结束后再计算电力系统的灵活性需求与灵活性供给。

表1 为各方案运行成本和灵活性平衡情况。方案1 因不考虑需求响应，且未对灵活性供需进行优化，因此电网出现了大量灵活性缺额。方案2 和3考虑了负荷的可转移特性，虽然需要付出一些调用补贴成本，但总运行成本与灵活性缺额均低于方案1。方案3 相比方案2 考虑了灵活性平衡约束，需要调用更多的需求侧资源，所以总运行成本略微增加，但灵活性缺额大幅减小，可以在小幅降低经济性的基础上保证系统的灵活性。方案4 的灵活性只由电源侧供给，虽然在电力平衡的基础上考虑了灵活性平衡约束，但仅对电源侧资源起作用，调整幅度不大，故仍然存在大量灵活性缺额，运行成本与方案1接近。

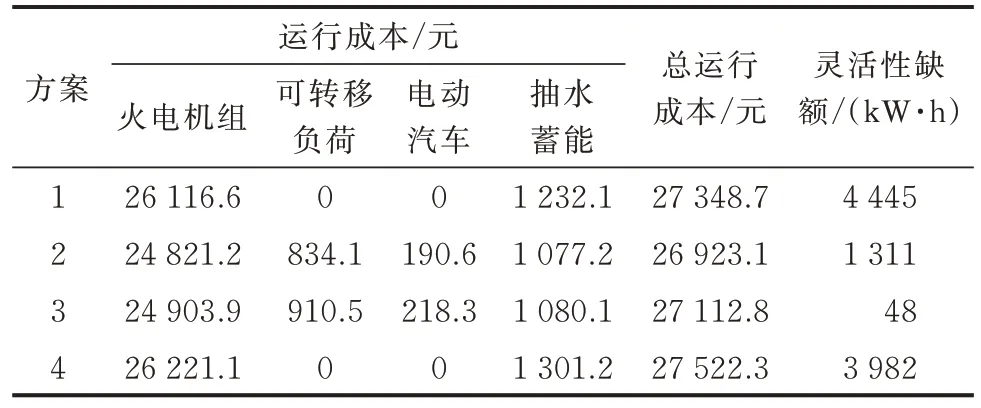
表1 各方案运行成本和灵活性平衡对比Table 1 Comparison of operation cost and flexibility balance of each scheme

4.2 灵活性资源的灵活性调节能力分析

本文在各类灵活性资源参与维持电网灵活性平衡的过程中引入了灵活调节因子，以反映不同灵活性资源对保证电网灵活性平衡的贡献程度。灵活性资源在t时刻的灵活调节因子越大，该资源灵活性调节能力越强。当各类资源的灵活调节因子之和小于1 时，表示电力系统在t时刻出现灵活性缺额。反之，当灵活调节因子之和大于1 时，表示灵活性留有备用。

图4 为方案3 中不同灵活性资源承担电网灵活性需求的贡献图，其中，红虚线表示灵活性资源完全跟踪电网的灵活性需求。

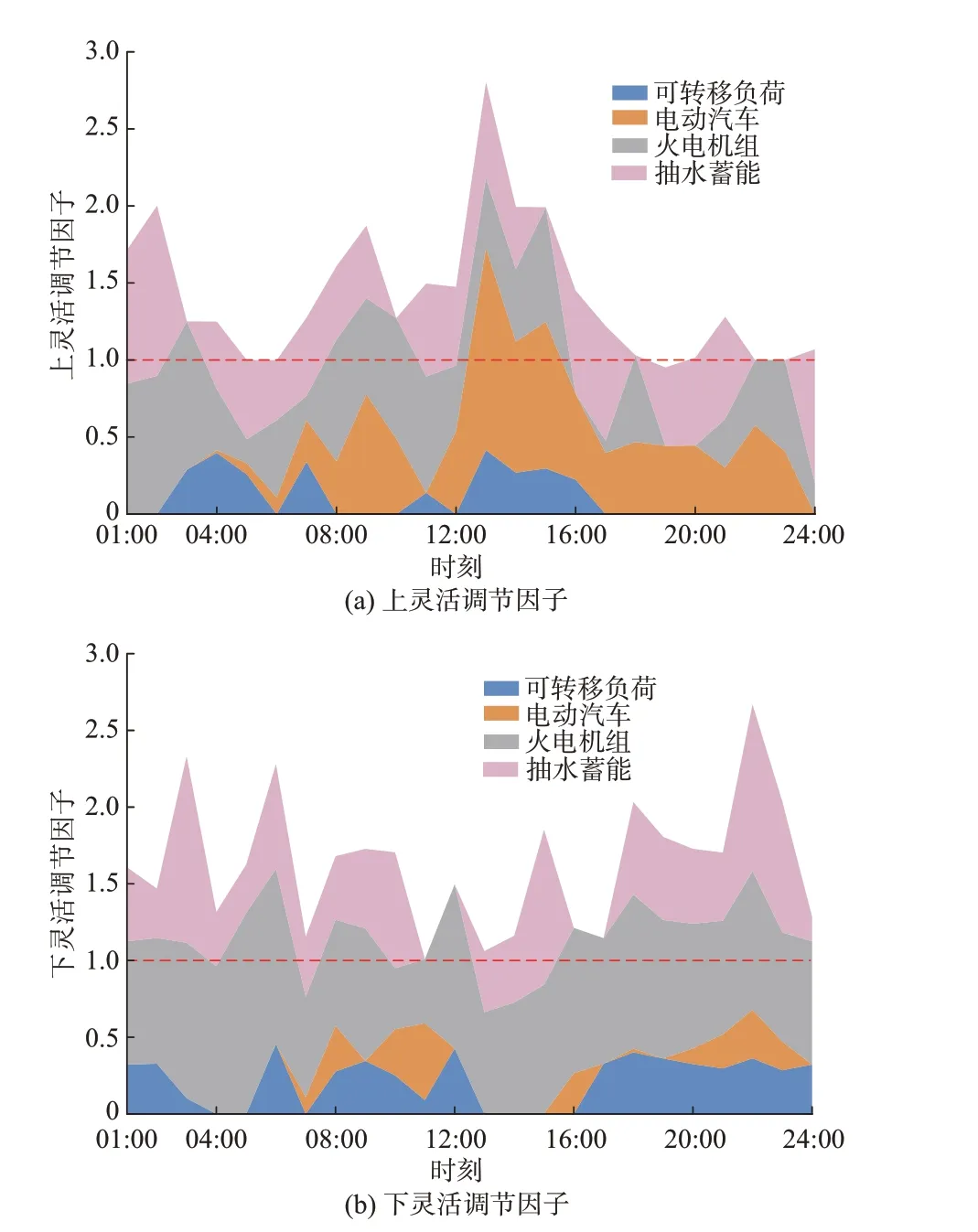
图4 不同灵活性资源灵活性调节能力Fig.4 Flexibility adjustment ability of different flexible resources

图4（a）中，19：00 时刻的灵活性调节因子之和在红线下方，代表该时刻灵活性出现缺额，与4.1 节中分析结果一致。由图4（a）和（b）可知，各类灵活性资源在各时段的灵活性调节能力均不相同。火电机组的灵活性受到容量和爬坡的限制，只能承受基荷，所以向下灵活性供给能力整体优于向上灵活性供给能力。在10：00—12：00 负荷低谷时段，火电机组运行在较低的出力水平，只能提供少量向下灵活性供给。在13：00—20：00 净负荷上升时段，火电机组向上灵活性仅有爬坡容量供给。抽水蓄能电站在净负荷波动剧烈处进行抽水和发电，具有较强的灵活性，有效弥补了火电机组在短时间内爬坡能力的不足。集群电动汽车在参与车网互动的过程中要考虑车主的出行需求：选择在12：00—16：00 净负荷低谷时段以最大功率充电，提供大量的向上灵活性；在19：00—21：00 晚高峰时段放电，由于受到电量需求的限制，只能提供少量向下灵活性。需要注意的是，在10：00 时刻附近，电动汽车也进行了放电，这是因为该时刻电网的向下灵活性存在不足的风险，由于本文考虑了灵活性平衡约束，集群电动汽车的充放电行为得到了充分的管理。可转移负荷受到用电需求与容量的限制，可以通过转移高峰负荷提供较小的灵活性，其向下灵活性供给的能力要略大于向上灵活性供给的能力。

4.3 数据驱动DRO 模型的保守性分析

给定不确定性概率置信度α1和α∞分别为0.5 和0.99，研究不同历史样本数M和削减的典型场景数K对DRO 模型保守程度的影响。

由表2 可知，随着历史样本数量的增加，电网各单元运行成本和灵活性缺额都在降低。这是由于历史样本数量的增加使得概率分布允许的偏差值θ∞和θ1相应减小，DRO 模型的保守程度得到了缓解。表3 为样本数据削减后典型场景数对模型保守性的影响，不难发现保守度随着场景数的增加而增加。这是因为随着典型场景数目的变多，削减后的场景分辨率变大，原来大量样本数据中的极端数据单独成为一类典型场景的概率变高。典型场景被刻画得越来越精细，更加接近风光负荷的真实波动范围，提高了模型的鲁棒性。

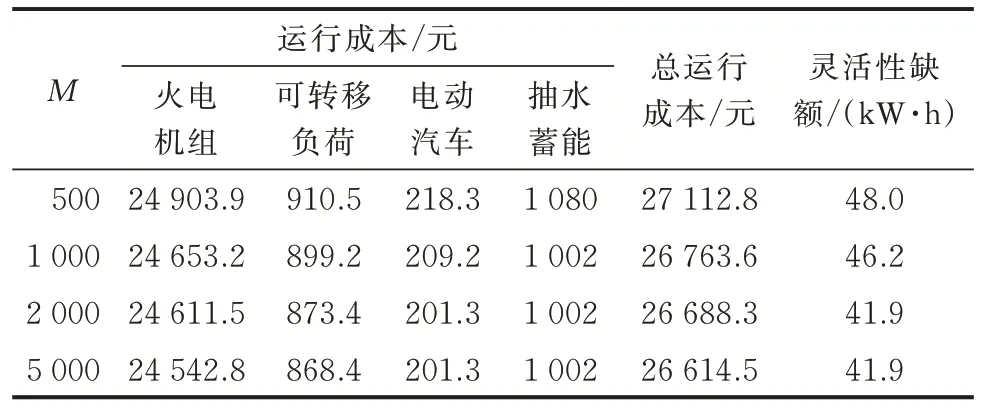
表2 历史样本数分析Table 2 Analysis of number of historical samples

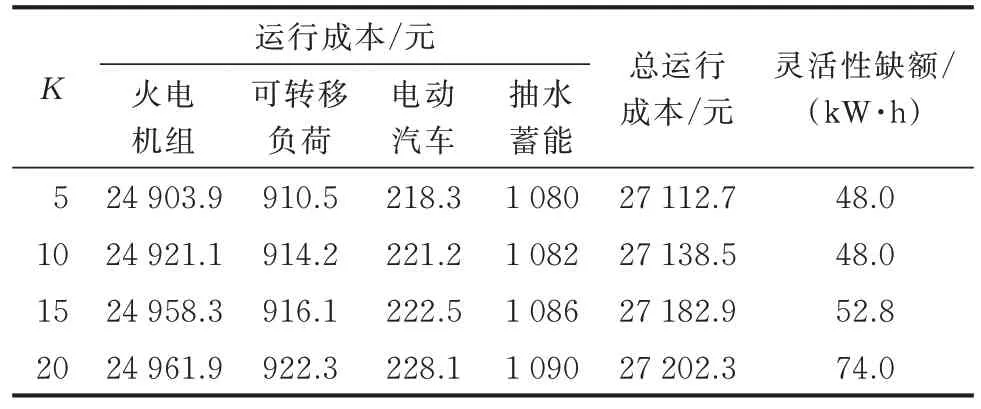
表3 典型场景数分析Table 3 Analysis of number of typical scenarios

本文DRO 模型的保守性体现在净负荷波动的恶劣场景发生概率变高，既反映了电力供需的静态平衡，又突出了电力供需的波动过程，即灵活性平衡过程。模型保守程度增加时，火电机组的成本变化很小，与其跟踪基荷有关。增加的总运行成本主要来自负荷侧资源的需求响应补偿成本，这使得电力系统灵活性缺额增加幅度较小，证明了所提模型的有效性。

4.4 同其他不确定性优化方法的对比分析

将考虑风光出力相关性的数据驱动DRO 模型（本文模型）与不考虑风光出力相关性的数据驱动DRO 模 型、传 统 两 阶 段RO 模 型、SO 模 型 进 行 比较。数据驱动DRO 模型的不确定性概率置信度α1和α∞分别为0.5 和0.99，样本数M和削减的场景数K分别取500 和5。4 种模型的结果如表4 所示。

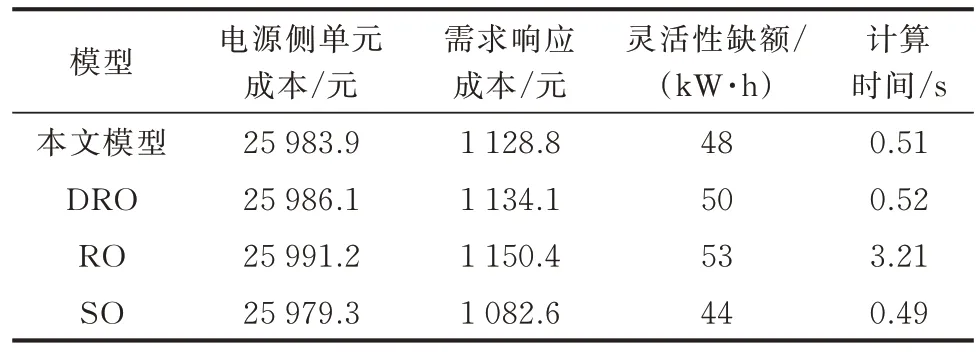
表4 不同模型结果比较Table 4 Comparison of results of different models

由表4 可知，4 种模型在电源侧各单元运行成本相差较小，在需求响应成本差别较大。RO 模型考虑不确定信息的最恶劣调峰爬坡场景，鲁棒性最强，所以各方面成本与灵活性缺额最大。数据驱动DRO 模型综合了RO 模型和SO 模型的优势，采用综合范数约束构建概率分布模糊集，具有更好的经济与灵活性，在日前调度阶段的经济性与鲁棒性取到了折中。当通过Copula 理论描述风光出力的时空相关性后，由于考虑了风光的互补性，计算得到的电网灵活性需求更小，本文所提模型相比不考虑风光相关性的数据驱动DRO 模型，保守程度更低。同时，由于数据驱动DRO 模型相比于RO 模型在子问题处理上不需要对偶处理，其采用的并行计算方式使得计算时间大幅降低。

下面将本文模型与SO 模型进行比较，进一步说明所提模型的优势。为便于说明，下文DRO 模型均指本文所提模型。

由表5 可知，DRO 模型的总运行成本与灵活性缺额在历史样本数不同时均大于SO 模型，这是因为DRO 模型考虑了最恶劣场景出现的概率分布，是保守性的体现。当历史样本数逐渐增大时，DRO 模型与SO 模型的结果趋于一致。这也说明DRO 模型有着良好的风险调节能力，运行管理者可以根据需求改变模型的保守程度。

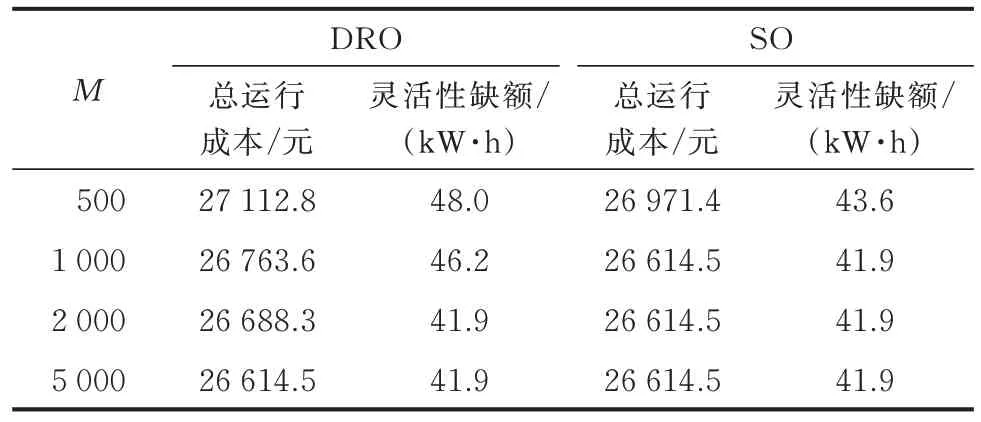
表5 数据驱动DRO 模型与SO 模型对比Table 5 Comparison between data-driven DRO model and SO model

需要注意的是，虽然DRO 模型比SO 模型保守，且日前阶段优化的运行成本与灵活性缺额更大，但是并不能说明SO 模型一定优于DRO 模型。因为新能源与负荷的日前预测具有误差，实际值与预测值的误差会造成日前确定的调度计划存在不平衡量，这部分差值需要系统在实时市场进行补偿。由于DRO 模型相较于SO 模型更多考虑了负荷与新能源的不确定性，鲁棒性更强。因此，虽然DRO 模型在日前调度成本与灵活性缺额较大，但在实时阶段有着更好的抵御不确定量波动风险的能力，总的成本与灵活性缺额可能更小。

为进行说明，本文采用DA-P（day-ahead programming）［11］策 略 进 行 实 时 能 量 的 补 偿。该 策略在日前计划的基础上仅通过购售电来平抑预测误差带来的功率波动，保证实时能量平衡。购售电价参考文献［22］。分别讨论两个模型在新能源与负荷处于不同实际值下的总运行成本。

图5 中的预测误差比值为新能源与负荷预测值偏离实际值的结果相对于参考曲线（取1 时等于附录B 中的预测值与实际值）的程度。不难发现，DRO 模型虽然在日前阶段成本高于SO 模型，但因其调度方案的鲁棒性较好，当预测误差比值较大时，实时补偿成本相较于SO 模型要小很多，从而总的运行成本也较低。但是，当预测精度较高时，如预测误差比值取0.5。此时，DRO 模型因为过于保守，在实时市场只能低价售出盈余的功率，导致经济性较差。

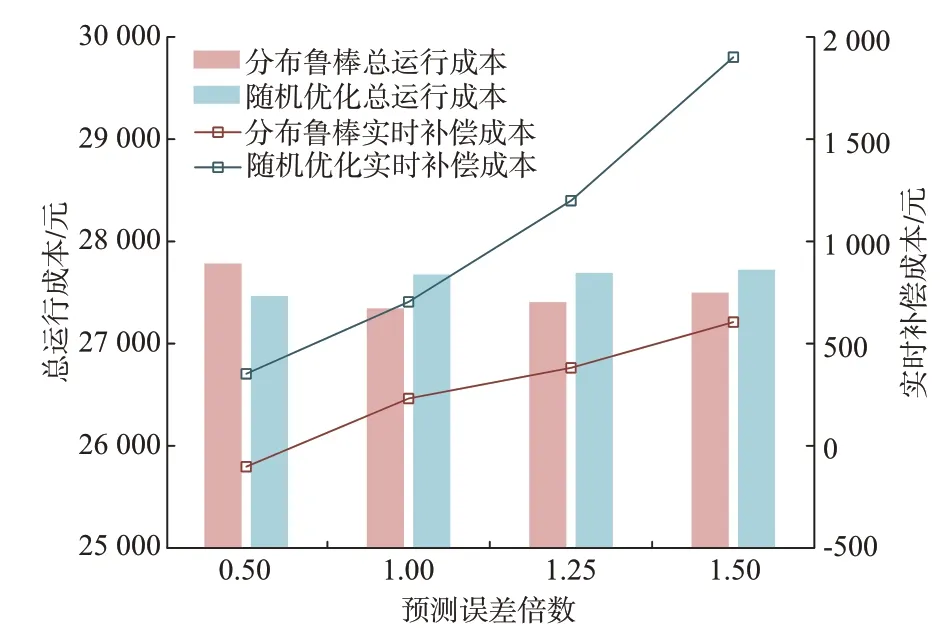
图5 不同预测误差比值下的优化结果比较Fig.5 Comparison of optimization results under different prediction error ratio

5 结语

本文提出一种考虑灵活性平衡的数据驱动DRO 模型，通过对比仿真算例，得出以下结论。

1）基于DRO 模型将区间法与场景法结合量化灵活性需求，可以充分考虑各场景下的净负荷波动。在灵活性供需平衡约束下，电动汽车、常规可转移负荷等负荷侧资源参与需求响应，可提供一定的爬坡容量，有效降低了净负荷的波动。考虑需求侧资源的灵活性供给能力后，电网的灵活性整体得到改善，特别是在爬坡需求较大的早晚高峰时段，灵活性裕度得到较大提升。在小幅降低经济性的基础上，保证了电力系统的灵活性。

2）数据驱动的DRO 模型基于历史数据样本充分考虑了风光负荷波动的不确定性，当保守程度增加时，电网需要给予负荷侧资源更多的经济补偿，激励其进行需求响应，从而提供更多的灵活性，以满足恶劣的净负荷爬坡场景。同时，DRO 模型不仅在日前调度阶段取得了经济性与鲁棒性的折中，而且在实时阶段有着更好的抵御不确定量波动风险的能力，总体经济性相比SO 模型更好。

本文对于电力系统灵活性供需平衡的研究，主要分析了电源侧与负荷侧的灵活性供给能力，尚未考虑电力系统的网络约束对于灵活性的影响。有研究指出，线路传输能力也可以提供一定的灵活性，分析源-网-荷-储的协同灵活性供给能力是下一步的研究工作。

本文研究得到华北电力科学研究院有限责任公司科技项目(Z2022KJ013)资助，谨此致谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。