基于深度学习的恒功率负荷直流微电网稳定性分析

2023-08-09宋冬然黄连生

电力系统自动化 2023年15期

杨建，刘笑，董密，李力，宋冬然，黄连生

（1.中南大学自动化学院，湖南省长沙市 410083；2.中国科学院等离子体物理研究所，安徽省合肥市 230031）

0 引言

随着风电、光伏等新能源技术的发展，新能源的供电可靠性和产能效率逐年提高。为了最大化新能源发电效益，文献［1-3］提出一种小型电力系统——微电网，用于解决新能源的接入问题。微电网在结构上，可分为直流微电网与交流微电网［1］。其中，直流微电网具有成本低廉、能源转换率高、易于控制等优点，并且不存在相位不匹配和无功功率供能问题，从而具有良好的发展与应用前景［4-6］。

然而，由于高比例电力电子装置的接入和恒功率负荷（constant power load，CPL）的存在，降低了直流微电网的系统阻尼［7］。同时，CPL 所表现出的非线性动力学和负阻抗特性容易导致直流微电网失稳［8-10］，尤其是在孤岛状态下这一问题更为突出［11］。因此，确定CPL 的稳定取值范围尤为重要。目前，主要采用基于机理模型的方法和基于时域仿真的方法来分析直流微电网的稳定性问题。

基于机理模型的方法又可以分为小信号和大信号2 种类型。在小信号分析中，主要利用线性分析工具（Bode 图、Nyquist 图、Routh-Hurwitz 判据和分岔理论）推导出直流链路的局部稳定条件［9-10，12-13］。相比于小信号而言，在大信号条件下稳定的系统在小信号条件下自然是稳定的，而相反的情况只有在某些特殊条件下才成立［8，14-15］。

近年来，研究人员主要采用非线性方法来分析带CPL 直流微电网的稳定性。文献［8，15］针对采用下垂控制的直流微电网，采用李雅普诺夫稳定性理论求解CPL 的取值范围。在此基础上，文献［16］采用深度学习方法构建李雅普诺夫函数，该方法可以降低保守程度。文献［17］提出一种基于混合势理论的方法，该方法适用于带单个CPL 或多个CPL 的直流微电网稳定性分析。在文献［18］中，波波夫绝对稳定性方法被用于分析CPL 交流微电网的稳定性。文献［19］开发出了一种稳定性分析工具，即用半定规划方法估计由多个CPL 组成的直流微电网吸引域。文献［20］针对电压控制和下垂控制2 种控制模式的直流微电网，分别计算其雅可比矩阵的特征值，进一步拓宽了稳定域。上述基于机理模型的理论分析方法，可以判断系统是否稳定，并求解CPL 的取值范围。然而，机理模型会忽略部分结构对系统的影响，导致模型误差会随着系统维度和复杂度的增加而逐渐增大［21-22］。

基于时域仿真的方法常用于研究系统的稳定性［23］。但直流微电网的时域仿真一次只能表明一组初始条件下的稳定性，而且需要较长的观察时间窗口，这导致时域仿真在评估速度上难以满足要求［22，24］。此外，理论分析方法和时域仿真方法无法提供系统参数与CPL 临界值之间的相关性强弱信息。

本文在分析直流微电网运行特点的基础上，针对带CPL 的直流微电网稳定性问题，提出一种基于深度学习的孤岛直流微电网CPL 临界值预测方法，并通过仿真和硬件在环实验验证了本文所提方法的有效性和优越性。

1 直流微电网及其稳定分析模型

1.1 直流微电网稳态模型

为建立直流微电网的大信号稳态模型，将带有下垂控制的源（droop control sources，DCS）等效为恒压源，电压值为母线电压期望值US，并将其与下垂系数（等效为虚拟阻抗）和滤波电感L、线路电阻R和母线电容C进行串联。CPL 等效为受控电流源，结合CPL 稳态模型，得到图1 所示的直流微电网稳态模型［8，25］。图中：PL1，PL2，…，PLj，…，PLm分别为第1，2，…，j，…，m个CPL 的功率，该CPL 等效为受电压控制的电流源，两端电压为母线电压ubus；d1，d2，…，dh，…，dn分别为第1，2，…，h，…，n个DCS 的下垂系数；i1，i2，…，ih，…，in分别为第1，2，…，h，…，n个DCS 的输出电流；ieq为源端支路电流之和。需要说明的是，当只有1 个DCS 时，本文设定下垂系数用d表示。

1.1.1 DCS 模型

为了保证直流微电网的稳定运行，需要确保功率平衡和母线电压的稳定。为此，源端变换器通常采用下垂控制，其效果等同于引入一个虚拟阻抗［8］。为了使输出电压偏差限制在可接受的水平范围内，需要对下垂系数d的取值范围进行限制，如式（1）所示：

式中：ifl为电源的满载电流；ΔVmax为所允许的最大电压差。

1.1.2 CPL 模型

为了在CPL 的输入端保持恒功率PL，反馈控制系统会强制输入电流（il）随着CPL 上电压的降低（增加）而增加（减少），对外表现为负阻抗特性。理想的CPL 为受电压控制的电流源［26］，其表达形式为：

1.1.3 线路阻抗等效电路模型

等效电路的模型为：

式中：deq为等效虚拟电阻之和；P为所有CPL 功率之和。

deq、ieq和P的计算公式如下：

1.2 直流微电网稳态分析

在上述直流微电网稳态模型基础上，本文先采用李雅普诺夫函数法来分析CPL 对直流微电网稳定性的影响。首先，通过联立式（3）和式（4）计算系统状态矩阵S，得到如下表达式：

然后，根据李雅普诺夫方程TS+STT=-Q，计算得到李雅普诺夫矩阵T为［8，26］：

式中：det(S)为S的行列式；Tr(S)为S的迹；Q为单位矩阵。

为了确保T为正定矩阵，需要满足如下2 个条件：

下垂控制允许母线电压存在±5% 的波动［8，26-27］，即：ubus∈[0.95，1.05]US。

由式（7）和式（8）可知，系统的稳定性受到参数d、L、R、C和P的共同影响。在这些参数中，CPL 是导致直流微电网失稳的主要原因［15-20］。因此，本文选择CPL 作为预测模型的输出特征，而将参数d、L、R、C作为输入特征。

2 CPL 临界值影响因素

为了确定影响CPL 临界值的因素，本文首先采用时域仿真方法获取样本数据；然后，利用最大信息系数（maximal information coefficient，MIC）进行相关性分析，以分析参数d、L、R、C与CPL 临界值Pc之间的关系。

2.1 系统稳定性标准

下垂控制器的存在会影响直流微电网的稳定性，在这种情况下，虽然系统处于李雅普诺夫意义下的稳定状态，但是实际上母线电压下降幅度已经超过所允许的最大波动范围值，如附录A 图A1 所示，此时系统实际上应该为失稳状态。因此，本文设定母线电压波动在±5%以内为稳定系统，否则为不稳定系统［8，26-27］，如下式所示。

式中：U(t；U0，t0)为母线电压幅值；U0为t0初始时刻的母线电压幅值。

2.2 相关性分析

由式（7）和式（8）可知，李雅普诺夫函数法能够分析出系统参数与Pc之间的正负相关性，但无法确定相关性的强弱程度。这也是利用李雅普诺夫函数、势函数等理论方法分析直流微电网稳定性的局限性之一。为此，本文提出采用MIC 方法进行相关性分析。与其他相关性分析指标相比，MIC 可有效监测两变量之间是否存在线性或非线性关系，并且具有稳健性，不易受到异常值的影响，是衡量变量间相关性的较好指标。MIC 的计算过程如下［28-29］。

1）计算给定变量A={d，L，R，C}与B={Pc}的互信息I（A；B）：

式中：a为给定A中的任一个变量；b为B中的变量；p（a）和p（b）分别为a和b的概率密度函数；p（a，b）为a和b两者的联合概率密度函数。

2）D为由A和B构成的一个有序的集合，其元素为（a，b）。定义网格G，其是将变量A的值域分成m段、B的值域分成n段形成的m×n网格，相同m×n的网格划分方式有多种，取不同划分方式中的I（A；B）最大值作为网格G的互信息值，并计算得到D在网格G划分下的最大互信息值Imax(D，m，n)为：

式中：I（D|G）为D使用G进行划分后的互信息值。

3）将D上不同网格G的所有最大互信息值归一化至（0，1）区间内，归一化的计算公式为：

式中：M(D)m，n为将不同网格G的最大互信息值归一化后的值。

4）在限制网格大小m、n的前提下定义集合D中2 个变量的最大互信息系数IMIC（D）为：

式中：ϕ（δ）为关于δ的函数，通常被设置为δ0.6。

3 CPL 临界值预测方法

本文采用深度学习的方法对直流微电网的CPL 临界值进行预测。其中，以参数d、L、R、C作为输入特征，Pc作为输出特征。

3.1 样本数据获取与预处理

首先，需要建立样本数据库，经过数据预处理后，将其输入深度神经网络（deep neural network，DNN）中进行训练。其中，样本数据库的建立尤为重要，因为它直接影响到模型的准确性和泛化能力。

3.1.1 获取仿真参数的区间

1）母线电容C的取值区间设定

通常情况下，母线电容C的取值区间可以通过式（8）求得。为了检验理论方法的保守程度，在含单个DCS 的简单直流微电网结构中，采用参数L=1 mF，R=0.04 Ω，d=0.3，P=15 kW 计算出母线电容的理论临界值为0.34 mF，但是采用时域仿真得到的临界值为0.1 mF。这表明采用基于机理模型的理论方法计算出的电容失稳值存在一定的误差。尽管其等效机理模型是正确的，但精确度仍不够。相比之下，本文提出的基于时域仿真的数据驱动方法可以更加精确地得到母线电容的临界值。

参数L、R和母线电容C本质相同，同属于线路阻抗，所以确定取值范围的方法与C相同。

2）下垂系数的取值区间设定

下垂系数d采用式（1）进行计算，根据式（7）和式（8）分析可知：CPL 临界值随下垂系数的增大先增大后减小。然而，下垂系数越大，母线电压参考值就越偏离期望值。考虑到保证系统的稳定性更为重要，为了更加全面地分析下垂系数对系统稳定性的影响，在低维系统中，下垂系数取值区间包含极值点信息；在高维系统中，适当减小下垂系数，以提高CPL 临界值。

3.1.2 数据获取

为了提升深度学习的泛化能力并有效挖掘直流微电网系统稳定性相关信息，样本的收集应该尽可能全面。本文根据直流微电网机理模型搭建不同仿真场景以获取初始数据，并依此建立数据库。因为考虑到参数的连续性不具有实际可操作性，所以对本文的变量进行离散处理后进行数据选取，以确保模型的可行性。

首先，由于DNN 在参数边界处的预测误差较为明显，本文在选取输入变量时将取值区间适当扩大。以下垂系数d为例，取值区间为［dmin，dmax］，经过边界处理后区间长度变为[d'min，d'max] (d'min＜dmin，d'max＞dmax)，其中，dmin和dmax分别为d的下限值和上限值；d'min和d'max分别为边界处理后d的下限值和上限值。然后，在经过处理后区间值的基础上，建立样本数据库。

1）针对低维系统(χ＜4，χ∈N+，其中，χ为DNN 输入特征的数量）采用遍历生成法（traversal method，TM）进行数据采集，系统参数值按固定步长在取值区间内遍历选取，生成参数组合后，固定每一组参数；然后，以定步长遍历CPL 取值区间，最终得到低维系统样本数据库。

2）在高维系统中，由于参数数量较多，使用遍历算法会十分低效。因此，本文采用随机数生成器（random number generator，RNG）生成法来随机生成参数组合。输入变量区间与低维系统一致，在参数区间内，随机选取系统参数值，然后，按固定步长遍历CPL 取值区间，从而获得高维系统的样本数据库。

3.1.3 样本数据预处理

在仿真数据中，通常存在异常数据和维度冗余的问题。为了解决此问题，本文按照如下步骤对样本数据进行预处理。

1）异常值处理

如果一组参数组合对应的实际CPL 临界值小于设定的最小CPL 临界值，那么这组参数就被视为异常数据。将这组参数的CPL 临界值设为0，这种规则称为承载力规则。

此外，异常数据还包括未采样数据点，如附录B图B1 所示的未知域。采用小步长验证法单独采样，找到CPL 临界值。

2）裕度处理

由于仿真模型与理想模型之间存在偏差而微电网对失稳情况的容错率又为0，在确定真实CPL 临界值的基础上，需要乘以小于1 的系数以保留一定的裕度。

式中：λ为系数；为缓冲功率值。

由于引入了小于1 的系数，最终用于训练的样本数据中的CPL 临界值λPc（向下取整），会小于仿真得出的实际CPL 临界值的实际值，这里将λPc称为裕度真值。附录B 表B1 中详细阐述了裕度处理过程。

3）误差模拟

为了提高神经网络的泛化能力，本文在DNN的输入特征x中随机加入符合标准正态分布的高斯白噪声Γ［30］，则输入特征变为x'：

式中：σ为噪声强度。

4）输入归一化

考虑到参数的量纲和数量级会对DNN 训练产生影响，本文采用min-max 方法对训练数据进行归一化处理［31］，如下所示：

式中：xw，n为归一化后的第w个DNN 输入变量的值；xmin和xmax分别为样本变量中的最小值和最大值。

通过上述数据预处理步骤，得到了预处理后的数据库。接下来，设计DNN 模型对数据库进行训练，以建立输入、输出之间的关系。

3.2 DNN 结构设计

从损失函数设计、DNN 模型性能评估出发，提出一种适用于直流微电网CPL 临界值预测的深度学习策略。

3.2.1 损失函数设计

DNN 预测模型如附录B 所述。在建立DNN 模型后，根据直流微电网的实际情况，本文设计了自定义损失函数（custom loss function，CLF）。每次训练同时输入ω组数据，第μ组输入参数xμ对应的输出结果为yμ，经过整数调整得到修正值y͂μ，y͂μ相对于yμ的绝对误差限为1，计算公式如式（17）所示。值得注意的是，修正公式是对输出层的结果进行修正，不对隐藏层的输出结果进行修正。

式中：ŷμ为裕度真值；floor（·）为向下取整函数；ceil（·）为向上取整函数；Δy为预测值与裕度真值的差值。

对于未超过CPL 的实际临界值y̆μ的训练结果（y͂μ≤y̆μ），则该组输入量被认为是稳定的，采用均方误差（mean square error，MSE）函数来计算损失函数J1：

如果DNN 预测值超过CPL 的实际临界值（y͂μ＞y̆μ），那么该组参数xμ定义为失稳点，在计算损失函数时给予极大的惩罚值J2：

式中：penalty（·）为惩罚函数，取极大值，计算结果远大于MSE 的计算结果。

综合式（19）至式（21），最终的损失函数J为：

此外，为了提高初始训练的速度和准确率，将CLF 放入训练次数的最后5%中，先前训练阶段采用MSE 作为损失函数。

3.2.2 网络参数设计

神经网络训练的本质是修改网络参数使损失函数达到最小。本文采用自适应矩估计（adaptive momentum estimation，Adam）方法更新参数。以权重值为例，在神经网络参数更新第z次后，神经元的参数为：

式中：qz和vz分别为第z次迭代的一阶和二阶矩估计；β1和β2为超参数；φ为一个小常数，用于避免除以零的情况；wzϑ，lr为第z次迭代的第ϑ层第l个神经元第r个输入值的权重值；α为学习率。

3.3 DNN 训练与验证

本文按照7∶2∶1 的比例将数据分为训练集、验证集和测试集。为检验预测算法的效果，本文采用MSE、平均绝对误差（mean absolute error，MAE）和失稳点数量3 个指标评价预测结果。

1）MSE 作为评价指标，与作为神经网络训练损失函数时的表达式相同，如式（18）所示。

2）MAE 的范围为［0，+∞）。当预测值与真实值完全吻合时等于0，即为完美模型；误差越大，该值越大。其表达式为：

式中：Ψ为数据集长度。

3）失稳点数量是指预测的CPL 临界值超过实际CPL 临界值的数量。理想情况下的结果是，在经过裕度处理后，所有预测结果都不会超过实际CPL临界值，这样失稳点的数量就为0，从而即使存在算法误差，DNN 预测结果也能够保证系统的稳定。

4 算例分析

本文所提出的MIC 和DNN 方法均在带有Pytorch 的Python3.8 环境中实现，计算机配备了2 个4 核Intel Broadwell 处理器、2 个Nvidia K40 图形处理单元和12 GB 内存。其中，图形处理单元用于训练阶段，加速DNN 训练，缩短训练时间。

为了保证分析结果具有代表性，本文建立了包含微源、变换器、控制器以及CPL 的通用型直流微电网。在不同算例中，根据仿真变量和CPL 建立不同的仿真场景。然后，基于上述仿真场景建立数据库，分析系统参数与CPL 临界值的相关性，并用于预测CPL 临界值。

4.1 低维场景分析

在低维场景中，直流微电网结构如附录C 图C1所示，结合具体仿真结果与3.1 节分析结果，本算例中使用的仿真参数取值如附录C 表C1 所示。在本算例中，依据变量的不同建立以下5 种不同的仿真场景。

场景F1：以C和P为变量建立仿真场景。

场景F2：以d和P为变量建立仿真场景。

场景F3：以L和P为变量建立仿真场景。

场景F4：以R和P为变量建立仿真场景。

场景F5：以d、L、R、C和P为变量建立仿真场景。

4.1.1 相关性分析

对仿真场景F1 和F2 的数据进行预处理后得到的可视化结果如附录C 图C2 和图C3 所示。仿真场景F3 和F4 的CPL 临界值为同一值24 kW。因此，后续不再单独计算关于参数L和R的MIC 值。

从附录C 图C2 可以看出，当母线电容取值区间为［0.8，2.5］mF 时，直流微电网所能承载的CPL 值最大，占比为37.78%。从附录C 图C3 可以看出，下垂系数与CPL 临界值成反比。当下垂系数取值超过0.6 时，CPL 临界值比较低，区间占比高达70.59%。

在分析可视化结果之后，采用MIC 方法对系统进行相关性分析。对于d，仿真场景F1 和F5 下的MIC 值分别为0.995 和0.990，取值区间分别为［0.1，1.8］和［0.1，1.4］；对于C，仿真场景F2 和F5 下的MIC 值分别为0.930 和0.070，取值区间均为［0.5，2.5］mF；对于L，仿真场景F5 下的MIC 值为0.080，取值区间为［0.1，1.5］mH；对于R，仿真场景F5 下的MIC 值为0.02，取值区间为［0.01，1］Ω。

由此可知，在线路阻抗与下垂系数的参数组合中，CPL 临界值受电容C的影响较弱，主要与下垂系数d有关。因此，在保证系统不失稳的前提下，采用下垂控制就可进行电压调节，且决定CPL 取值范围，其他变量可以不考虑。因此，在后续算例中，单独采用下垂系数d作为DNN 输入变量，并取消仿真中参数L、R、C的变化。

4.1.2 低维场景的预测性能评估

为验证所设计DNN 预测模型的有效性，依据边界法将母线电容C扩至［0.1，3］mF，下垂系数d的取值范围为［0.1，1.9］，并建立样本数据库。随后分别使用自定义的CLF 和MSE 损失函数进行训练，预测结果如表1 所示。对比CLF 和MSE 的结果，采用CLF 作为损失函数时的误差均小于MSE。此外，场景F1 和F2 预测准确率全部达100%。因此，采用CLF 作为损失函数，更有助于提高DNN 方法对CPL 临界值预测的准确率，同时，可以保证失稳点数量为0。在计算速度方面，DNN 预测模型在线评估速度为百微秒级，可快速预测CPL 临界值。

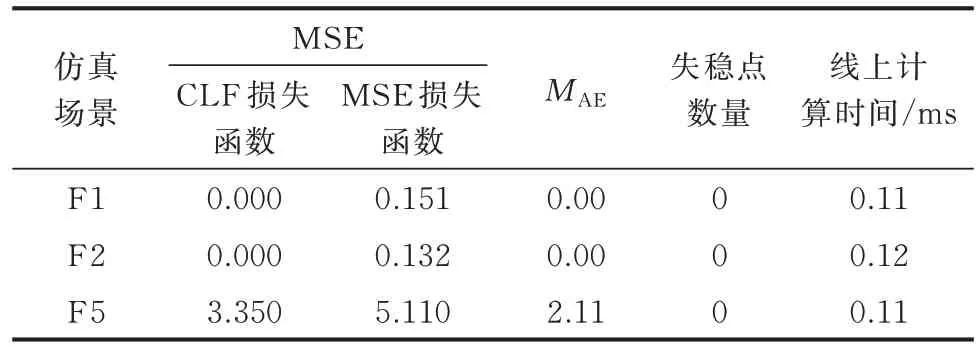
表1 预测性能评估结果Table 1 Evaluation result of prediction performances

将场景F5 与F2 进行比较，通过相关性分析降维之后，DNN 预测准确率得到较大幅度提升，MAE降低2.11，MSE 降低3.350。

在场景F1 中，对预测效果进行仿真验证，结果如图2 所示，以此来证明样本数据的有效性以及检验DNN 预测模型的有效性。其中，图2（b）、（d）、（f）的P为DNN 预测值，分别为10、16、2 kW。经过裕度处理后（λ=0.90），预测结果均分别小于对应的实际临界值（12、18、3 kW），并且母线电压未发生振荡且未超过稳定范围下限380 V。因此，系统稳定，这表明DNN 预测的CPL 临界值可以保证系统稳定。在图2（a）、（c）、（e）所示的结果中，P分别为15、21、6 kW，均分别大于对应的实际临界值。此时，母线电压值小于稳定范围下限380 V。因此，系统已经失稳，这表明建立CPL 的样本数据有效。

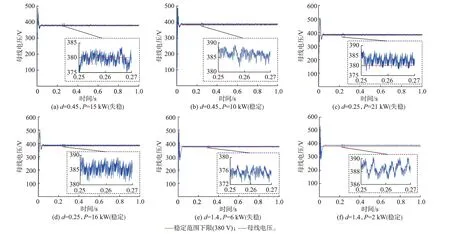
图2 场景F1 的直流母线电压波形Fig.2 Waveforms of DC bus voltage in scenario F1

结合表1 和图2 的预测结果和仿真验证结果，DNN 可以准确预测CPL 临界值，并且可以保证系统稳定，同时，提供一定的功率裕量。

4.2 高维场景分析

4.2.1 高维仿真场景的DNN 预测性能

为了验证本文所提出的深度学习策略在高维直流微电网中预测CPL 临界值的效果，设计了如附录C 图C4 所示的高维仿真结构。由式（1）可知，高维系统中适当减小下垂系数可以增大CPL 临界值。因此，在仿真场景F6 高维系统中，下垂系数d取值范围为［0.15，0.55］。在此场景下，高维数据库的样本量充足，无须再采用边界扩充法解决数据量不足的问题。

此外，为了提高DNN 的泛化能力，根据高维仿真场景的训练数据库生成相同分布的高斯白噪声。然后，与样本数据直接线性相加，用于模拟参数的不精确情况。预测结果如下：采用CLF 和MSE 损失函数得到的MSE 分别为1.46 和2.13；MAE为0.819；失稳点数量为0；线上计算时间为0.13 ms。所有预测结果都不超过实际CPL 临界值，这表明在高维状态下，本文提出的基于DNN 的稳定性分析方法既可以较为精准地预测CPL 临界值，又可以保证系统稳定。

4.2.2 仿真验证

在场景F6 中，随机生成10 组数据进行验证。结果如表2 所示，DNN 的预测值均小于CPL 临界值（其中，λ=0.95）。

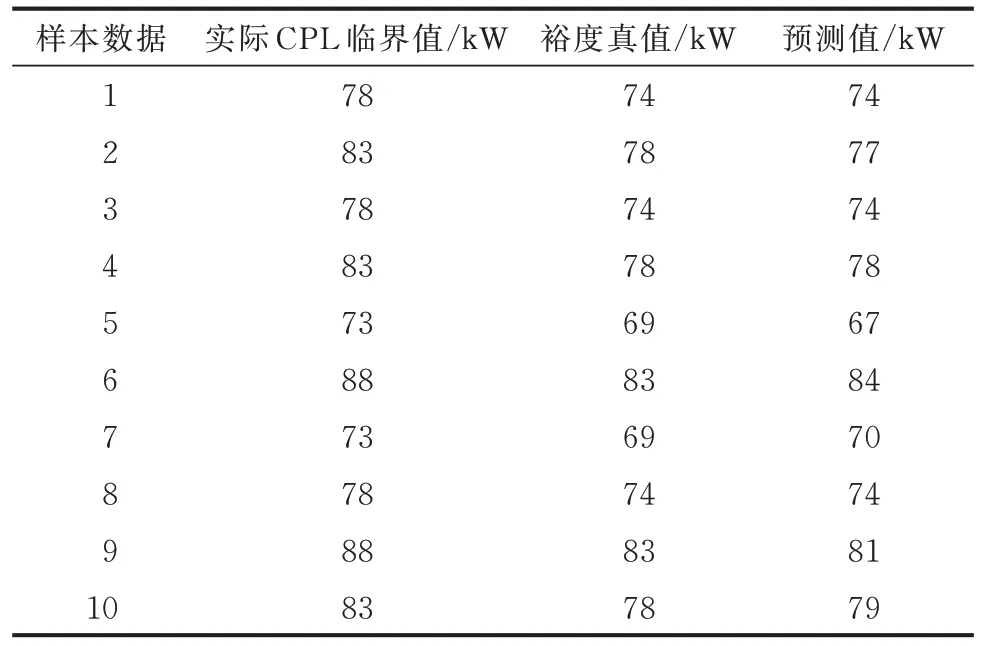
表2 深度学习策略的随机检验结果Table 2 Random test results of deep learning strategy

对预测结果进行仿真验证，结果如图3 所示。图3（a）和（c）中多源下垂系数的取值分别为［0.43，0.40，0.44，0.36，0.21，0.41，0.43，0.37，0.39］和［0.42，0.22，0.30，0.26，0.40，0.31，0.43，0.25，0.27］，P为DNN 预测值，分别为74、78 kW。在经过裕度处理后（λ=0.95），预测结果均小于实际CPL 临界值78、83 kW。此时，母线电压未发生振荡且未超过稳定范围下限380 V，因此，系统处于稳定状态。由此可知，DNN 预测的CPL 临界值可以保证系统稳定。

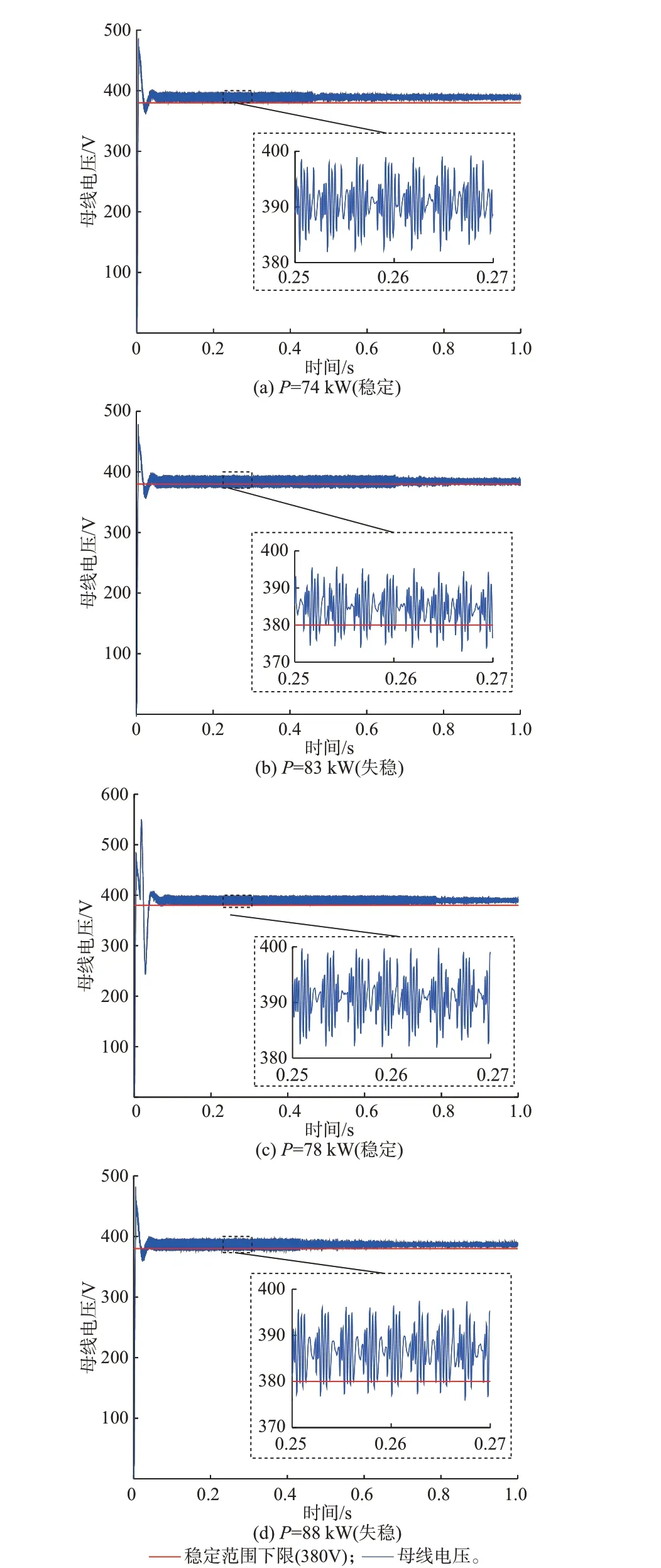
图3 场景F6 的直流母线电压波形Fig.3 Waveforms of DC bus voltage in scenario F6

图3（b）和（d）的下垂系数取值分别与图3（a）和（c）相同，P分别为83、88 kW，均分别大于对应的实际临界值，此时，母线电压值小于稳定范围下限380 V。因此，系统处于失稳状态，证明了样本数据的有效性。

4.2.3 DNN 参数的选择

在DNN 预测模型中网络层数设为4，迭代次数为1 500，学习批次选择为1，神经元个数为2 000。需要说明的是，学习率α设置的不同，其预测结果也会大相径庭。综合考虑预测效果和时间成本，最终设定学习率α=0.000 04。学习率对预测效果的具体影响如附录C 图C5 所示。

4.3 算法比较

与传统理论分析方法相比，本文所提出的方法考虑了直流微电网母线电压降落的失稳情况，更加全面地反映了直流微电网的真实电压稳定情况。同时，又可以体现参数d、L、R、C与CPL 临界值相关性强弱的信息。

当然，机器学习同样可以作为预测模型，本文将所提出的方法与支持向量机（support vector regression，SVR）、高斯过程回归（gaussian process regression，GPR）、决策树（decision tree，DT）和随机森林回归（random forest regression，RFR）方法进行对比。3 种场景F1、F2 和F6 在不同方法下的预测结果如表3 所示，DNN、SVR、RFR 方法的预测误差结果见附录C 图C6。

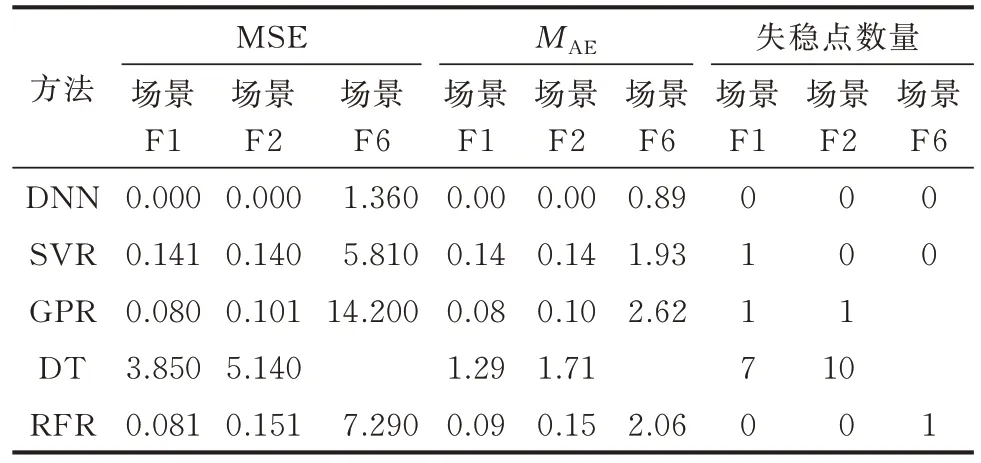
表3 不同算法预测结果比较Table 3 Comparison of prediction results of different algorithms

从表3 可以看出，DNN 方法在所有场景下都能保证失稳点数量为0，且DNN 的预测精度最高。随着维度的增加，所有预测方法准确率都有所下降，但DNN 的预测准确率仍保持最高。此外，从附录C 图C6 的误差分布来看，DNN 预测结果误差较小，误差分布较为均衡；而RFR 与SVR 方法的预测误差分布较为分散，而且存在误差较大的情况。上述分析结果表明，在解决直流微电网CPL 临界值问题中，DNN 方法更有优势。

5 实验验证

为进一步验证本文所提出的CPL 临界值预测方法的有效性，建立了具有6 个微源的直流微电网实验场景。所有微源连接带下垂控制的Buck-Boost变换器（200～400 V），CPL 连接Buck 变换器（200～400 V）。硬件在环实验在RT-LAB 和设备OP5707中进行，实验设备如附录D 图D1 所示。

首先，建立实验场景获取样本数据库，参数如附录C 表C1 所示，实验场景所用的下垂系数取值区间和精度分别为［0.1，1.0］和0.01，结构如附录D 图D2所示。然后，采用DNN 学习下垂系数与CPL 临界值之间的映射关系，这里λ=0.95。预测结果如下：采用CLF 和MSE 损失函数得到的MSE 分别为0.620 和1.170；MAE为0.39；失稳点数量为0；线上计算时间为0.12 ms。预测误差（见附录D 图D3）以及硬件在环实验结果（见附录D 图D4）进一步说明了DNN 可以精准预测裕度真值，并且经过裕度处理后，预测结果不会超过实际CPL 临界值，同时又可以为系统提供一定的功率裕量。