曲面反射装置对脉冲爆轰发动机外流场影响的数值模拟
2023-08-08康杨李宁黄孝龙张君善翁春生
康杨, 李宁, 黄孝龙, 张君善, 翁春生
(1.南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094;2.武警工程大学 装备管理与保障学院, 陕西 西安 710086)
0 引言
脉冲爆轰发动机(PDE)是一种基于爆轰燃烧,利用周期性爆轰波和高温高压燃气产生推力的新型动力装置,具有热效率高、比冲高和推重比大等优点,是航空航天领域研究的前沿与热点[1]。然而,PDE在工作时产生的强噪声会对发动机工作性能和以其为动力的飞行器运行安全构成严重威胁[2]。
爆轰噪声的两个来源分别为爆轰波逸出管口与化学反应区解耦而成的爆轰冲击波和爆轰波波后的高速燃气射流激波[3]。Anand等[4]通过实验详细地研究了气态燃料PDE的工作频率、当量比、填充系数、可燃混合物氮气稀释率、喷管结构等参数对爆轰噪声的影响,并对比了双管与单管PDE噪声特性。Xu等[5-6]和Huang等[7]、黄孝龙等[8]搭建了汽油/空气两相PDE爆轰噪声实验系统,通过理论和实验相结合的方法对单管和多管PDE爆轰噪声的波形、声压级、持续时间和指向性等声学特性进行了系统研究。Kang等[9]、康杨等[10]实验研究了椭球型反射罩和环形喷管对PDE爆轰噪声传播特性的影响。上述研究表明,爆轰噪声属于典型的脉冲噪声,声压级高,频谱覆盖范围宽,具有显著的周期性和指向性,会对实验人员和实验环境造成一定的噪声污染。
为削弱PDE工作时产生的大功率爆轰噪声对发动机关键部件的影响以及对实验人员的听力损伤,将爆轰噪声汇聚在发动机出口下游方向能够极大限度减少爆轰噪声向发动机头部的传播。目前常见的冲击波和声波汇聚方法有声波透镜法[11]、阵列聚束法[12]以及曲面反射法[13]。PDE工作时产生的高温高压燃气对声透镜具有一定损伤,因此声透镜法并不适用。阵列聚束法需要多个PDE共同协作,不适用于抑制单个PDE工作时产生的爆轰噪声向上游的传播。依据曲面反射法设计的曲面反射装置是一种常见的冲击波和声波聚焦装置,根据曲面反射法的作用机理,曲面反射装置的特殊几何性质使声波在传播过程中经过反射后的传播方向发生变化,并汇聚到某一特定区域,具有指向性好、稳定性高等优点,在冲击波与声波汇聚和传播的研究中具有重要意义。因此,将反射装置加装在PDE的尾部会对PDE出口附近的流场结构产生较大的影响,显著改变近场爆轰流场中冲击波和燃气射流激波的传播特性,将爆轰噪声汇聚于发动机出口下游方向,实现对飞行器及操作人员的安全防护。此外,Boesch等[14]提出爆轰管可作为一种可重复且稳定产生大功率声波的新概念声源。反射装置对PDE出口流场的作用效果必然影响PDE下游的噪声能量分布,若反射罩能提升下游特定方向或特定区域内的噪声能量,将能拓展声源的应用范畴,因此探索反射装置对PDE外流场的影响,对于利用爆轰产生强噪声的新概念声源的工程化应用也具有重要意义。
考虑到反射装置旋转面的复杂边界,本文采用非结构三角形网格时空守恒元和求解元方法(CE/SE方法)对以汽油/空气为燃料/氧化剂的气-液两相PDE的内外流场进行二维轴对称数值模拟,分别研究椭球型、抛物线型以及圆锥型反射装置对PDE外流场的影响,探索不同反射装置对爆轰冲击波在PDE下游方向的汇聚效果。
1 控制方程与物理模型
1.1 控制方程
采用基于双流体模型欧拉-欧拉控制方程对气-液两相爆轰过程进行模拟。由于两相爆轰的复杂性,做出以下简化与假设[15-17]:PDE物理模型为轴对称结构,忽略爆轰管内强化燃烧装置;忽略汽油的雾化过程以及汽油和氧化剂的掺混过程,液滴均匀分布于气体中并将液滴颗粒群视为连续介质处理;汽油液滴呈球形且液滴的初始直径相同,单个液滴内温度均匀分布,忽略液滴的重力作用以及液滴间的相互作用;激波扫过后,液滴不破碎并保持球形,在激波后的高速气流作用下仅发生剥离,且液滴剥离蒸发后成为气体,与空气瞬间均匀混合;液滴在经过剥离和蒸发过程转化为气体后瞬间完成化学反应并释放能量;忽略PDE管壁与外界的热交换,化学反应释放的能量仅被气体吸收。
根据上述简化与假设,得到的气-液两相PDE轴对称控制方程[15-17]为
(1)
式中:φg、φl分别为气相和液相的体积分数比,满足φg+φl=1.0;ρg、ρl分别为气相密度和液相密度;ug、ul分别为气相和液相的轴向速度;vg、vl分别为气相和液相的径向速度p为压力;Eg、El分别为液相和气相单位总能,
(2)
eg、el分别为气相单位内能和液相单位内能;Id为液滴蒸发和剥离引起的单位体积液滴的质量变化率[15-19],
(3)
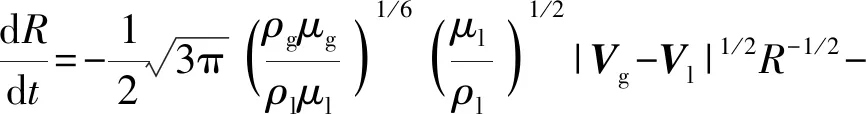
Tg、Tl分别为气相温度和液相温度,上式右边第1项为剥离项,第2项为蒸发项,n为单位体积中液滴的颗粒数,R为液滴半径,μl为液相动力黏性系数,|Vg-Vl|=[(ug-ul)2+(vg-vl)2]1/2,λ为气体的热传导系数,Nu为努塞尔数,L为燃料液滴的蒸发热;Fdx、Fdy分别为气体作用于单位体积混合物中液滴上的力[15-18]Fd在x、y方向的分量,
(4)
(5)
(6)
(7)
μg为气相动力黏性系数,Qd为单位体积气-液两相的交换热[20],
Qd=4πR2nλNu(Tg-Tl)/(2R)
(8)
Qc为单位体积化学反应释放热,
Qc=Idqf
(9)
qf为液相的燃烧热。
1.2 计算模型与初始及边界条件
两相PDE轴对称计算模型如图1所示,计算模型中将计算域划分为内流场和外流场区域。内流场区域为PDE爆轰管,轴向x方向取爆轰管管长1.5 m,径向y方向由于计算模型的轴对称性取爆轰管管径的1/2,即0.03 m。为节省计算资源,将PDE外流场区域分为区域Ⅰ和区域Ⅱ,当PDE外流场未发展至区域Ⅱ中时仅计算区域Ⅰ。PDE外流场总计算域轴向x方向为2.8 m,径向y方向为1.5 m。

图1 两相PDE轴对称计算模型
在计算过程中,内流场初值条件为:PDE爆轰管内填充均匀分布的化学当量比为1的汽油液滴/空气混合物。其中,液态汽油燃料和空气的初始温度及初始压力分别为298 K、0.1 MPa,汽油液滴的初始半径为50 μm。外流场的初值条件为:PDE外流场布满均匀分布的空气,空气的初始温度和初始压力分别为298 K和0.1 MPa。在PDE左端封闭端附近区域x/l≤0.01,y/y0≤0.5内施加2 980 K和1.5 MPa 的高温高压条件进行点火,其中l为PDE管长,y0为PDE管半径,如图1中的红色区域所示。
计算过程中的各边界条件分别为:内流场计算中PDE的左边界和上边界采用固壁边界条件;对称轴采用轴对称边界条件;PDE出口采用非反射自由边界条件。外流场计算中PDE出口边界采用入流边界条件;对称轴采用轴对称边界条件;外流场左边界、上边界和右边界均采用自由边界条件,流出后的物质将不再对计算流场产生影响。
1.3 计算方法及源项处理
由于反射装置的复杂边界,本文采用基于非结构三角形网格的CE/SE方法对控制方程进行编程求解。CE/SE方法是近年来求解守恒律方程的一种新的数值方法,该方法将时间与空间统一对待,从守恒律积分方程出发,设置守恒元与求解元,计算格式在局部和全部计算区域内严格保证物理意义上的守恒,具体计算格式参考文献[21-22]。

1.4 数值验证
利用PDE内流场爆轰波参数对本文采用的计算方法和化学反应模型进行验证。表1为在PDE中心轴线管口位置处爆轰波压力和波速与NASA CEA(Chemical Equilibrium with Application)软件[23]计算的理论C-J爆轰参数的对比。由于CEA软件中不包含液态汽油燃料,选用汽油燃料中重要成分气态C8H18的爆轰参数作为理论对比。由表1可以看出,计算结果的爆轰压力与CEA理论C-J爆轰压力值相对误差较小,爆轰波波速相对误差为9.06%。这是因为两相爆轰过程中液滴需要经过剥离蒸发这一物理现象把液滴变为气体后才能发生化学反应,所以两相爆轰的化学反应区域长度要明显大于气相爆轰,由此造成计算得到爆轰波波速的误差相对较大。Wang等[15]的研究中也指出,当两相爆轰的数值计算误差在10%内时,可认为计算方法和计算模型的准确性得到验证。

表1 计算结果与理论C-J爆轰参数的对比
为验证数值计算中PDE内外流场所采用网格的收敛性,取外流场中远离PDE出口区域的网格为内流场网格尺寸的3倍,在计算域内划分的非结构三角形单元总数分别156 550、291 440和697 499。不同网格尺寸条件下压力在PDE爆轰管轴线上的分布如图2所示。图2表明,在3种网格下均能有效地捕捉到爆轰强间断面,为节省计算成本,在本文计算中采用内流场各边界处网格单元边长2 mm,总数为30多万三角形网格,即能满足计算要求。

图2 网格无关性验证结果
图3为PDE出口压力随时间变化曲线的实验与二维轴对称数值计算结果对比。实验中的爆轰管管径、长度等结构参数以及燃料氧化剂的填充系数和当量比均与计算中保持一致。从图3中可以看出,实验得到的爆轰压力为2.03 MPa,而运用非结构三角形网格CE/SE方法捕捉到的对应工况下的爆轰压力为2.01 MPa,与实验相比误差为0.2%,在合理误差范围内。对比实验结果和计算结果的波形发现,实验得到的爆轰波压力波形和计算所得爆轰波压力波形的变化趋势基本一致,但实验测得的压力曲线出现了明显的压力振荡,计算所得压力曲线光滑。这是因为在计算中为简化计算,没有考虑爆轰管内复杂装置以及湍流、摩擦、燃料雾化和燃料/氧化剂混合等因素,所以未出现类似实验压力曲线的复杂波动情况。

图3 PDE出口压力计算结果与实验结果对比
本文主要研究PDE内外流场发展特性,未求解爆轰波精细结构。图4为PDE在爆轰和排气过程中不同时刻的内外流场压力云图。从图4中可以看出:在PDE点火后t=0.94 ms,爆轰管内已经形成稳定发展传播的爆轰波,且爆轰波传播至1.38 m处,爆轰压力为2.03 MPa;t=1.01 ms时,爆轰波传播至爆轰管管口处;t=1.07 ms时,爆轰波已经传播出PDE管口并失去了能量的支持迅速蜕化为前导激波,并以球形向下游传播至x=1.56 m位置附近,压力为0.3 MPa。同时,在PDE管内产生了一系列膨胀波向PDE头部传播,降低了PDE管内压力。紧随前导激波的是管内喷射的高压爆轰产物形成的球状膨胀波,膨胀波后产生低压区。随着时间的推移,激波沿轴向和径向方向同时传播,逐渐衰减,在t=2.54 ms时刻,爆轰产物也与管外大气急剧混合、形成多个高低压区。由此可见,爆轰噪声本质上是通过两种来源产生的:爆轰波蜕化而成的冲击波和从管口喷射处的爆轰产物燃气射流。从PDE管口附近的压力场云图可以看出,非结构三角形网格CE/SE方法可以清晰地刻画流场变化过程和细节。

图4 PDE外流场不同时刻压力云图
2 反射装置对PDE外流场的影响
采用非结构三角形网格CE/SE方法数值模拟椭球型反射罩、抛物线型反射罩和圆锥型反射罩对PDE外流场的影响。计算中,内外流场的计算域与1.2节两相PDE轴对称计算模型中的计算域相同,唯一不同的是在PDE尾部加装了反射装置。3种反射装置的计算模型如图5所示,Ref-1~Ref-3反射装置分别为椭球型反射罩、抛物线型反射罩和圆锥型反射罩。其中,PDE出口BC位于Ref-1~Ref-3反射装置中轴线200 mm处,反射装置的其他参数见图5。加装不同反射装置的两相PDE轴对称计算模型的初值条件与1.2节中相同。边界条件中,反射装置的旋转面AE采用壁面边界条件,非结构三角形网格将旋转面AE划分为若干与坐标轴不平行的斜壁面,在非结构三角形网格CE/SE方法中对此类斜壁面的边界条件的处理比较复杂,具体可以参考文献[21],反射装置的出口ED采用自由边界条件,其余边界条件均与1.2节中相同。经网格收敛性检验,分别取3个算例中的非结构三角形网格数为285 238、286 946、289 870。

图5 不同反射装置计算模型
2.1 加装椭球型反射罩的PDE流场分析
为便于观察反射装置对PDE外流场冲击波以及燃气射流传播过程的影响,将上半平面计算得到的结果对称地画在下半平面,从而得到一个完整的子午面图线。图6详细刻画了加装椭球型反射罩的PDE外部流场结构,清楚地描述了PDE管口的冲击波与椭球型反射罩作用反射后的传播与衰减过程。图6(a)~图6(h)分别为爆轰管点火后1.48 ms、2.36 ms、4.27 ms、6.00 ms、6.81 ms、7.16 ms、7.41 ms和8.00 ms时的压力场。在PDE点火后t=1.48 ms,PDE爆轰管内部形成稳定传播的爆轰波传播出PDE爆轰管出口,并以球面波形式在外流场传播。一部分冲击波和爆轰产物燃气射流作为直达波进一步向下游传播,此时已传播至x=1.8 m位置附近,压力为0.136 MPa;另一部分向上游方向传播至椭球型反射罩的椭球面,反射前的压力为0.102 MPa。在t=2.36 ms时,向上游传播的冲击波和燃气射流被椭球型反射罩反射,传播方向发生变化、形成反射波。由于中心轴线上x<1.5 m区域内爆轰管的存在,直至t=2.36 ms时,由反射罩壁面反射形成的反射波才避免了爆轰管外壁对其的二次反射、直接传播至中心轴线上。此时直达波已经传播至轴线上x=2.13 m处,直达波和反射波均在椭球型反射罩的区域中,压力分别为0.118 MPa和0.115 MPa,反射波压力小于直达波压力。在t=4.27 ms时,直达波传播处椭球型反射罩出口,此时冲击波在椭球型反射罩出口尖角处的衍射产生衍射波,以尖角为中心的球面衍射波向PDE轴线方向传播。在t=6.00 ms时,直达波和反射波均传播出椭球型反射罩区域,二者在中心轴线上的压力值分别为0.105 MPa和0.132 MPa,反射波的压力高于直达波压力。由此可见,随着传播距离的增加,反射冲击波的能量在聚焦过程中不断增强,在反射罩的中轴线上出现压力汇聚区域,产生高压区。由尖角衍射产生的负压不断向轴线传播,负压影响区域不断增大。在t=6.81 ms时,直达波传播至椭球型反射罩的汇集焦点处,反射波在汇聚焦点前,此时反射波是凹形的收敛波形。当反射波越来越接近汇聚焦点,在t=7.16 ms时,反射波的内凹程度减弱。在t=7.41 ms时,反射波传播至汇聚焦点x=3.5 m处,此时反射波压力峰值为0.122 MPa,反射波整体呈现X形,即前端呈现内凹形、后端呈现外凸形。当反射波传播通过汇聚焦点后,在t=8.00 ms时,反射波转变为凸形发散波向下游传播。可见当PDE出口位于椭球型反射罩的一个焦点处时,椭球型反射罩聚焦效果明显,具有较高的指向性,但其作用距离也受反射罩尺寸的限制,当反射波传播过汇聚焦点后会迅速发散。

图6 加装椭球型反射罩的PDE不同时刻压力云图
2.2 加装抛物线型反射罩的PDE流场分析
图7为加装抛物线型反射罩的PDE流场压力云图。由图7可见,与加装椭球型反射罩的PDE流场相似,在PDE点火后t=1.48 ms,爆轰波传播出PDE爆轰管出口,并以球面波形式在外流场传播。一部分冲击波和爆轰产物燃气射流作为直达波进一步向下游传播,另一部分向上游方向传播至抛物线型反射罩的抛物面。在t=2.36 ms时,向上游传播的冲击波和燃气射流被抛物线型反射罩反射,传播方向发生变化、形成反射波。在t=4.95 ms时,直达波已经传播至抛物线型反射罩外的区域,反射波也传播至反射罩出口位置。抛物线型反射罩的出口尖角产生以尖角为中心的球面衍射波。在t=6.00 ms时,直达波和反射波均已传播出抛物线型反射罩区域。对比椭球型反射罩的计算结果分析可知,当直达波和反射波均传播至反射罩区域后,加装抛物线型反射罩的PDE外流场中的直达波和反射波的传播速度差值相较椭球型反射罩更大,反射波落后于直达波较长,轴线上的反射波压力更低。抛物线型反射罩扩大了反射波在径向方向上的作用范围,将反射波近似平行反射至PDE下游,对反射波具有一定的汇聚作用。

图7 加装抛物线型反射罩的PDE不同时刻压力云图
2.3 加装圆锥型反射罩的PDE流场分析
图8为加装圆锥型反射罩的PDE流场压力云图。从图8中可以看出,加装圆锥型反射罩的PDE外流场与加装椭球型反射罩和抛物线型反射罩的PDE的外流场差别很大。在圆锥型反射罩外部未出现明显滞后于直达波的反射波,反射波增宽了直达波轴向x方向的高压区,提升了直达波的压力,加强了直达波的强度并与直达波一起向下游传播,因此圆锥形反射罩的PDE外流场不存在由反射波引起的二次压力峰值。

图8 加装圆锥型反射罩的PDE不同时刻压力云图
2.4 不同反射装置对轴线上的压力分布影响分析
图9为加装椭球型反射罩、抛物线型反射罩、圆锥型反射罩和无反射罩的PDE外流场中心轴线上不同监测点处的压力-时间曲线。图9(a)对应x=2 m处,该观测点在反射装置凹腔区域内;图9(b)对应x=2.5 m处,该观测点位于反射装置出口处;图9(c)和图9(d)分别对应x=3 m和x=3.5 m处,这两个观测点在反射装置反射面外。
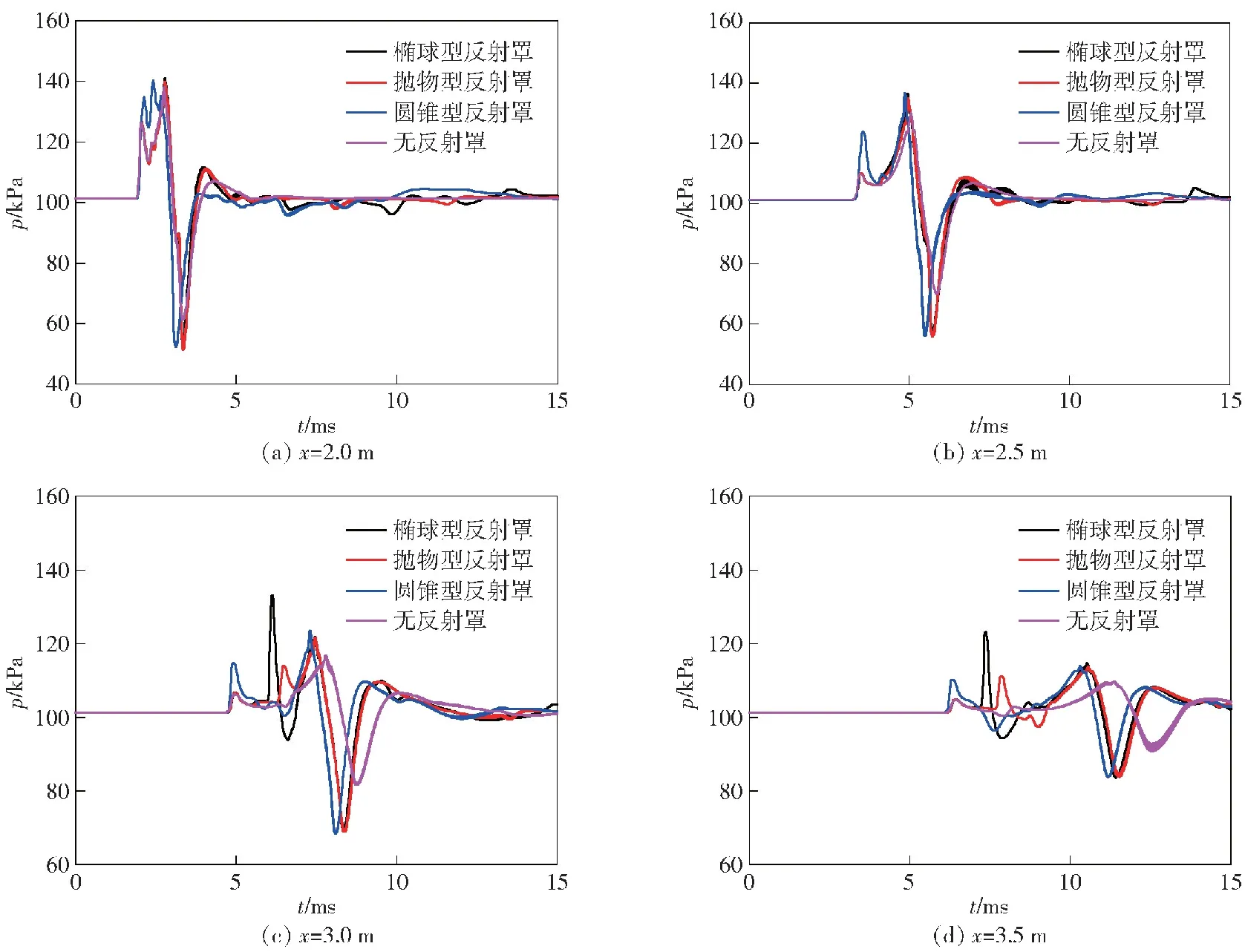
图9 不同观测点处的压力-时间曲线
以无反射罩PDE中心轴线上的压力变化为基准,结合图6、图7和图8中管外流场压力云图进行分析。从图9(a)中可以看出,在反射装置凹腔区域中,圆锥型反射罩凹腔中的压力反射汇聚上升最早,出现在负压到来前,此时反射波延迟直达波0.29 ms达到测点;椭球型和抛物线型反射罩的压力反射汇聚上升稍晚,出现在负压后,反射波延迟直达波约1.9 ms到达测点。加装椭球型和抛物线型反射罩的压力变化趋势与未加装反射罩时的压力变化在负压前几乎一致。从图9(b)中可以看出,随着传播距离的增加,当直达波和反射波传播至反射装置的出口处时,直达波和反射波的压力下降。椭球型和抛物线型反射罩在该测点的压力变化趋势与x=2 m处一致,而在圆锥型反射罩的压力曲线上反射波压力尖峰消失,结合图9(c)、图9(d)进行分析,在x=2.5 m测点位置处由圆锥形反射罩所形成的反射波与直达波汇聚,压力时间曲线的第1个压力峰值显著高于其余工况。从图9(c)和图9(d)中可以看出,在反射装置外的测点处,由椭球型反射罩形成的反射波压力最高,在x=3 m和x=3.5 m处时分别为133 052 Pa和123 180 Pa。结合压力云图可以看出,椭球型反射罩外的高压区域汇聚在中心轴线附近,中心轴线上的压力值相较于无反射罩、抛物线型和圆锥型反射罩时更高,说明椭球型反射罩对PDE外流场冲击波的汇聚效果更为显著,在反射装置中心轴线方向具有较高的指向性。
3 结论
本文采用非结构三角形网格CE/SE方法,针对PDE以及加装椭球型反射罩、抛物线型反射罩和圆锥型反射罩的PDE内外流场进行数值模拟。结果表明,椭球型和抛物线型反射罩的曲面反射作用能够将原本向上游传播的冲击波和燃气射流在流场中形成显著滞后于直传波的反射波。椭球型反射罩将反射波汇聚于轴线附近,而抛物线型反射罩则将反射波以近似平面波的形式向下游反射汇聚。此外,椭球型反射罩所形成的反射波在反射装置外测点处的压力值更高,传播速度更快,在轴线上的汇聚效果相较于抛物线型反射罩和圆锥型反射罩更好,具有较高的中心轴线方向的指向性。
在实际工程应用中,可以根据三类反射装置的不同反射特性和具体需求选用,计算结果可以提供一定的理论指导。本文研究结果对PDE噪声防治和爆轰噪声的特殊场景化应用具有重要意义。
