喷水量及喷水位置对部分进气轴向涡轮机性能影响特性
2023-08-08智若阳罗凯王瀚伟秦侃
智若阳, 罗凯, 王瀚伟, 秦侃
(西北工业大学 航海学院, 陕西 西安 710072)
0 引言
提高涡轮前燃气入口温度是提供较大可用焓降及提升涡轮机有效功率的手段,如今水下航行器涡轮机入口温度升高到1 100 ℃[1],造成涡轮盘热负荷过大,在高转速运转下易发生结构的龟裂变形,影响涡轮机的安全与稳定工作,而利用航行器外部充足的海水对涡轮盘进行冷却,是确保涡轮机安全稳定运行的首选方案。研究喷水冷却对水下涡轮机产生的影响,对进一步提升涡轮机输出功率具有十分重要的理论意义和工程价值。
目前,射流冲击冷却常被应用于航空涡轮叶片的内部冷却中,尤其是涡轮叶片的前缘区域,但其冷却介质多为空气[2]。朱卫兵等[3]采用在叶片内安装导流片并布置射流孔的方式对高温叶片进行冲击冷却,对改善冲击冷却效果的方法进行了实验研究。阎鸿捷等[4]对涡轮叶片的前缘冲击-气膜复合冷却结构的内部传热特性进行了实验研究,获得了不同雷诺数下该冷却结构的传热与流阻特性。Liu等[5]对涡轮叶片前缘切向射流冲击的流动和换热特性进行了实验和数值研究,发现切向射流的换热特性与喷嘴位置和射流雷诺数有关。席雷等[6]对类前缘通道内蒸汽射流阵列冲击冷却的流动与传热特性进行了数值模拟,得到了不同雷诺数、孔径比和孔间距比下的流动及传热性能规律。
在其他领域,国内外还针对射流冲击相变冷却开展了相关研究。姜澎等[7]对水雾/蒸汽相变冲击冷却系统进行了数值模拟,得出雾滴气化的吸收热量对于冷却作用的贡献比较大的结论。叶纯杰等[8]使用雷诺应力湍流模型对半封闭垂直射流冲击移动平板进行数值分析,发现平均努塞尔数以及冲击点处的平板表面湍流强度随平板移动速度的增大而增大。Metzger等[9]对单个静止气体喷嘴冲击旋转加热的圆盘进行了实验研究,结果表明在旋转主导工况下,换热速率与射流流量基本无关。Guo等[10]使用微型针状喷头进行射流冲击研究,研究表明沸腾传热可以通过增加总面积和射流冲击速度来提高换热系数。李炎军等[11]采用数值模拟的方法研究了滑油射流冲击旋转壁面的流动与换热特性,结果表明壁面平均传热量与射流流速和壁面转速有关。
要准确仿真涡轮机冷却问题还需要开展流-热耦合分析,卢康博等[12]使用流-热耦合的方法对涡轮机背盘冲击冷却的冷却特性进行了仿真研究,结果表明背盘冲击冷却可以大幅度降低径向涡轮背盘的温度。赵瑞勇等[13]对某型液体火箭发动机部分进气涡轮进行了气-热-固多学科耦合数值仿真,结果表明涡轮转子受到强烈的气动、热交变力冲击,其结构强度问题变得尤为突出。李磊等[14]在对船用高压比大流量增压器优化的过程中综合考虑了流-热-固耦合影响,提高了增压器涡轮整体性能。肖炎斌等[15]对水下小型特种燃气轮机轮盘流-热耦合进行了仿真分析,发现在不采取任何冷却措施的情况下,轮盘最高温度已超出材料最大耐受温度。
综上所述,目前国内外对涡轮机的冷却研究集中在航空涡轮机的领域,冷却介质多为空气,而液体冷却在其他领域已有广泛应用,对于水下部分进气轴向涡轮的冷却规律特别是对喷水冷却的涡轮机研究甚少;此外,流-热耦合方法也已经广泛应用到全周进气涡轮机,但对于部分进气结构以及水冷工质的涡轮机流-热耦合的研究较少。
本文采用液态水作为介质对水下涡轮机进行冷却并进行流-热耦合仿真,分析了轴向喷水和径向喷水两种喷水位置以及不同喷水量对涡轮盘的温度、热应力和热变形的影响,为水下涡轮机的喷水冷却策略提供了参考。
1 数值模型
液相水射流冲击冷却轮盘换热的过程涉及液相水与水蒸气的质量、动量和能量交换,以及流体和固体之间的能量交换,需要求解连续性方程、动量方程、能量方程和组分输运方程。
1.1 控制方程
1.1.1 流体域的控制方程
由于在冷却的过程中发生了沸腾蒸发现象,水和水蒸气的连续性方程[16]为
(1)
式中:ρq为q相的密度;αq为q相的体积分数;vq为q相的速度;Sq为q相的质量源项。
动量守恒方程[16]为
(2)
式中:ρ为密度;v为速度;p为压力;μ为黏度;Sm为动量源项。
能量守恒方程[16]为
(3)
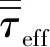
1.1.2 固体域的控制方程
固体域的计算采用三维稳态无内热源导热,其控制方程[16]为
(4)
在流-热耦合的过程中,流体域和固体域之间的热传递是通过对流换热实现的,固体域内部存在导热,当达到稳态时,耦合边界处温度及热流相对值等于零,即
qs=qf
(5)
Ts=Tf
(6)
式中:qs和qf分别为固体和流体耦合面处的热流密度;Ts和Tf分别为固体和流体耦合面处的温度。
1.2 相变模型和源项
计算时需在能量方程和质量方程中引入相变模型以仿真液态水的沸腾现象。本文采用Lee相变模型[17],该模型具有计算精度高、形式简单及收敛性好等优点[18]。
液相水的质量源项为
(7)
式中:r为相变传质系数;αf为液相水的体积分数;ρf为液相水的密度;Tsat为水蒸气的饱和温度。
动量源项为
Sm=vSf
(8)
能量源项为
Se=Sfh
(9)
式中:h为汽化潜热,由美国国家标准技术研究院[19]的物性参数库获取并拟合为温度的关系式:
h=-14.86T2+1.025×104T+4.174×105
(10)
1.3 组分输运模型
为确定喷水涡轮中燃气和水蒸气的分布状态,需要使用组分输运模型,控制方程[16]为
(11)
式中:Ji为组分i的扩散通量;Di,m为混合物中组分i的质量扩散系数;μt为湍流黏度;Sct为湍流施密特数;Yi为组分i的局部质量分数;DT,i为热扩散系数。
1.4 湍流模型
本文采用SSTk-ω(k为湍流动能,ω为湍流频率)湍流模型来描述混合气体的湍流现象,具有较高的模拟精度和数值稳定性,k和ω的方程[16]为
(12)
(13)
式中:d和e分别表示坐标方向;u为速度;x为坐标;Gk为由于平均速度梯度而产生的湍流动能;Gω表示湍流动能ω的生成;Γk和Γω分别表示k与ω的有效扩系数;Yk和Yω分别表示k与ω的湍流扩散项;Dω表示交叉扩散项。
此外,本文采用Coupled求解器,使用有限体积法离散控制方程,梯度离散方法采用基于网格中心的最小二乘法,压力离散方法采用PRESTO!格式,流动方程和标量方程的对流项的离散方法均采用1阶迎风格式。
1.5 流-热耦合模型


图1 流-热耦合仿真方法流程
部分进气涡轮机流-热耦合计算方法的步骤如下:

步骤2在轮盘处使用周向平均的方法,在转子处使用相对位置平均的方法,对热流密度和近壁面温度进行平均,得到耦合面上的对流换热系数hc:
(14)
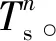
步骤4将固体域耦合面的壁面温度进行松弛,其计算公式为
(15)
式中:β为松弛因子。将松弛后的结果作为流体域耦合面的壁面边界条件,并再次对流体域进行数值模拟。
步骤5重复步骤1~步骤4,直到壁面温度收敛。
1.6 热弹性力学分析
涡轮盘因温度场的作用会产生热变形,表达式为
εT=α(Tt-Tref)
(16)
式中:εT为热变形;α为线膨胀系数;Tt为涡轮盘的温度;Tref为参考温度。
涡轮盘的热应力则可由下式计算:
σT=Ey×εT
(17)
式中:σT为热应力;Ey为材料的杨氏模量。
2 模型验证
为验证数值模型的有效性,采用Kiely等[20]开展的2 kW部分进气涡轮机实验,验证部分进气涡轮数值仿真模型;采用Kuhn[21]开展的竖直管中水蒸汽-不凝气体对流冷凝换热现象的实验,验证两相传质换热模型;采用水下部分进气轴向冲动式涡轮机喷水冷却实验,验证涡轮机喷水冷却仿真方法;采用Back等[22]开展的冷却喷管中的流-热耦合实验,验证流-热耦合数值模型。
2.1 部分进气涡轮数值仿真模型验证
为验证部分进气涡轮数值仿真模型的准确性,本文采用Kiely等[20]开展的2 kW部分进气涡轮机实验,该实验所用涡轮机的参数如表1所示,边界条件如表2所示,计算域网格如图2所示。

表1 Kiely等[20]轴向涡轮机的参数

表2 Kiely等[20]轴向涡轮机的边界条件
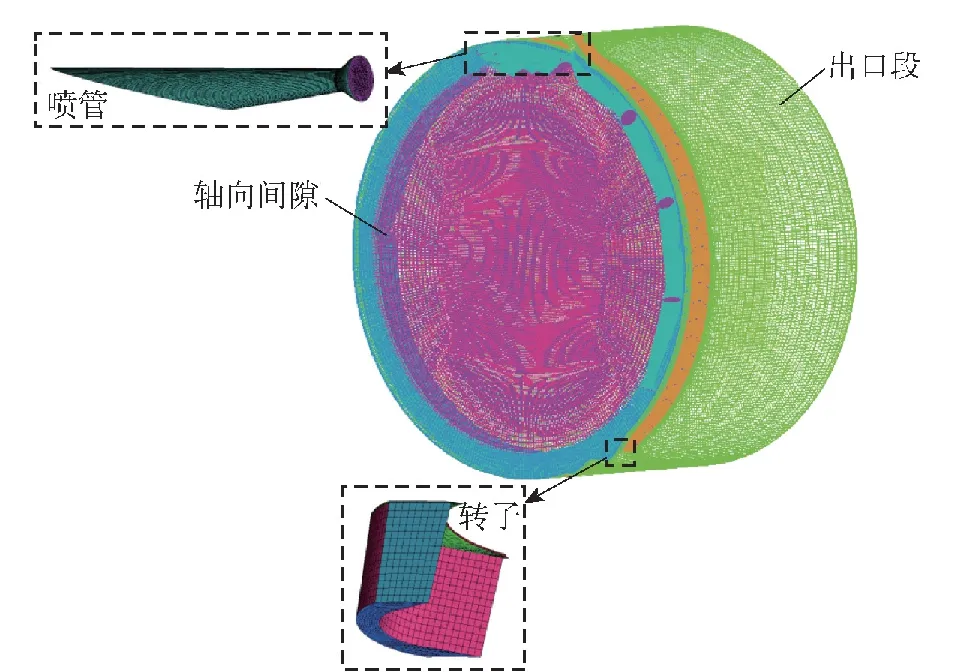
图2 实验涡轮的计算域网格
由表3可知,仿真结果与Kiely等[20]实验参数误差在3%以内,验证了本文仿真方法的准确性。

表3 仿真结果与实验参数对比
2.2 两相传质换热数值模型验证
为验证两相传质换热数值仿真模型的合理性,本文采用Kuhn[21]开展的竖直管中水蒸汽-不凝气体对流冷凝换热现象的实验,并建立了相应的二维轴对称数值计算模型,如图3所示,仿真中的不凝气体为空气,不凝气体的质量分数为0.15。
实验中冷凝段的壁面温度作为仿真中冷凝段的壁面温度条件,如图4所示。数值仿真得到的轴线温度与实验结果的对比如图5所示,轴线温度的最大相对误差在1%以内,说明本文数值仿真方法合理,有较高的精度。

图4 冷凝段的壁面温度
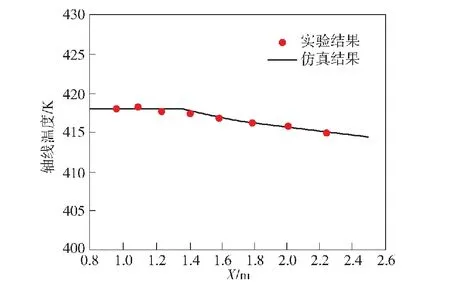
图5 轴线温度对比
2.3 涡轮机喷水冷却仿真方法验证
为进一步验证本文所建立的涡轮机喷水冷却仿真方法的合理性和准确性,对数值模型进行验证,验证算例为水下部分进气轴向冲动式涡轮喷水冷却实验,该实验的实验装置如图6所示。

图6 涡轮喷水冷却实验装置
根据实验中的水下涡轮机,建立水下涡轮机流体域的计算域网格如图7所示,采用六面体结构化网格,近壁面处设置边界层,在喷管流域、轴向间隙流域采用O型网格进行加密,喷管靠近喉部位置沿流动方向进行加密,流体域网格数量在1 085万左右。

图7 部分进气涡轮的流体计算域
选择喷水冷却涡轮机的3组实验工况进行数值仿真,边界条件如表4所示,实验1作为最大实验工况,将实验1的边界条件和实验结果当作无量纲数1,实验中测量涡轮机的功率和出口处的气流温度作为验证数值模型准确性的参照,仿真过程中Lee模型的相变传质系数取值为10,后续按照该系数进行相关计算。
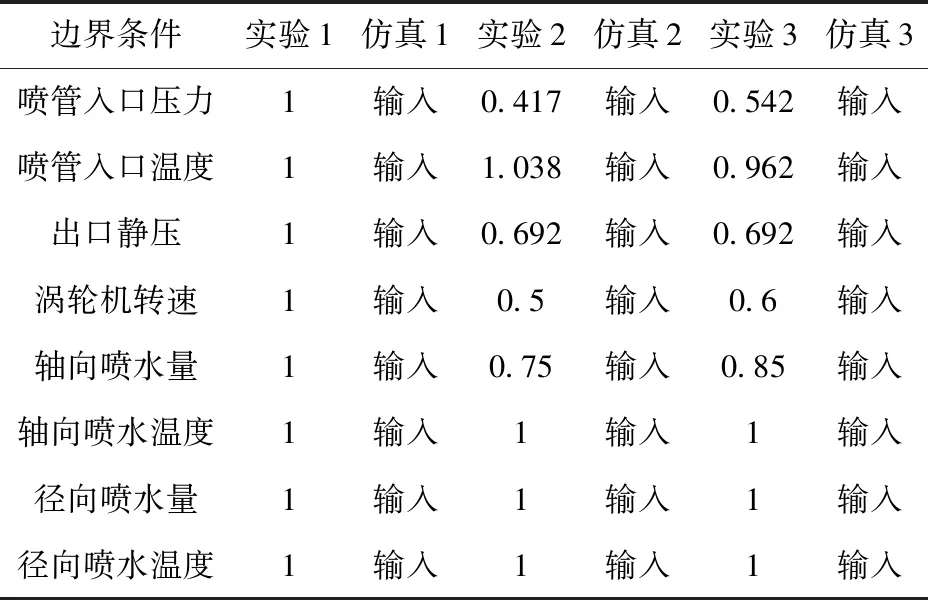
表4 喷水冷却涡轮的边界条件
按照上述工况对水下涡轮机进行数值模拟,仿真结果与实验结果的对比如表5所示,3种工况输出功率的相对误差分别为0.5%、6.4%和10.8%,出口测点温度的相对误差均在5%以内,说明本文数值模型合理。
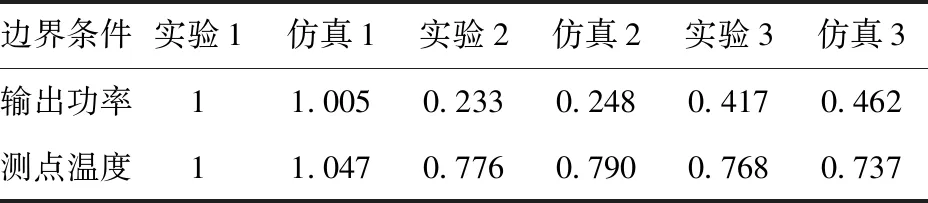
表5 仿真结果与喷水冷却实验结果对比
2.4 流-热耦合模型验证
为验证流-热耦合模型的有效性,本文采用Back等[22]开展的冷却喷管中的流-热耦合实验,建立了相应的数值计算模型,如图8所示,流体域为理想空气。

图8 验证喷管的几何模型及边界条件
实验中喷管的外壁温度作为仿真时的外壁面的温度边界条件(见图9),固体材料的热导率设定为27 W/(m·K)。数值仿真结果与实验结果对比如图10所示,可以看出喷管内壁面的温度误差在4%以内,说明本文数值计算方法合理,精度较高。

图9 喷管外壁面的温度

图10 喷管内壁面温度分布比较
由上述4个验证实验对部分进气轴向涡轮机喷水冷却流-热耦合数值仿真方法进行了充分验证,下面介绍仿真过程并对仿真结果进行分析。
3 数值仿真与分析
3.1 物理模型
喷水涡轮流-热耦合仿真计算需要用到水下涡轮机的流体域和固体域模型,流体域模型如图7所示,固体域的计算域网格如图11所示,采用六面体结构化网格,固体域与流体域的流-固耦合交界面网格相互对应,网格节点误差在0.01 mm以内,固体域网格数量在960万左右。
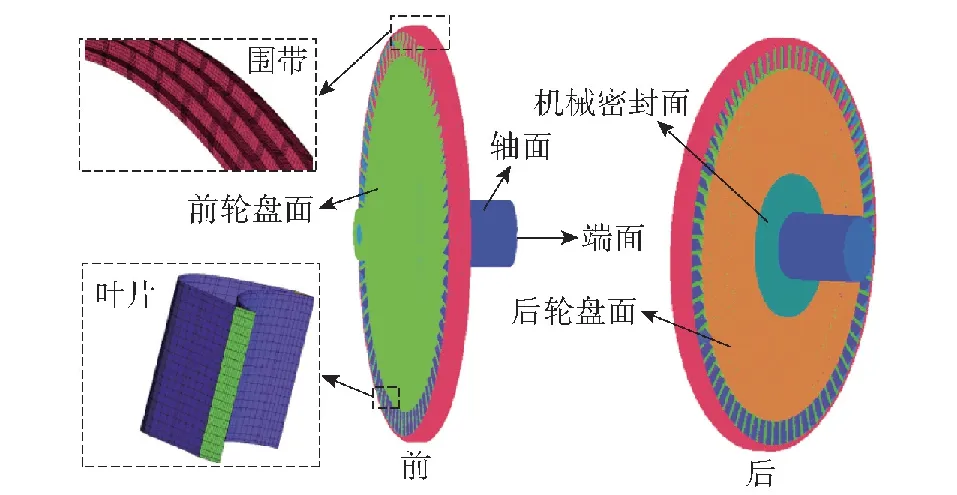
图11 部分进气涡轮的固体计算域
水下涡轮机固体计算域中的机械密封面与密封装置相连,燃气无法流入,固体域中除机械密封面、轴面和端面以外,其余面均为流-固耦合交界面。
3.2 边界条件
为评估喷水冷却对部分进气涡轮性能的影响,分别在轴向和径向方向上喷出不同流量的冷却水,如表6所示,为获得不同冷却水量和不同冷却水位置对涡轮盘温度分布及应力应变分布的影响,本文共分析了5种不同工况下涡轮机的性能。轴向和径向的冷却水温度均为298.15 K。
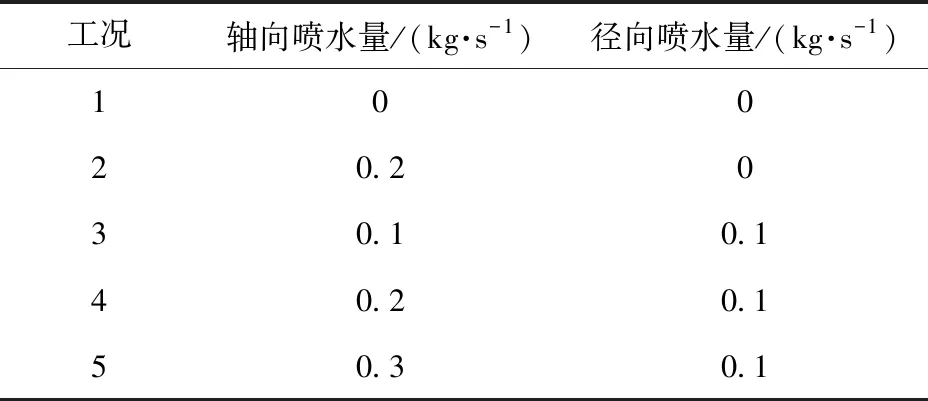
表6 冷却水的边界条件
涡轮机流体域和固体域的边界条件如表7所示。采用稳态仿真的方法,并在数据传输过程中采用混合平面的方法以考虑瞬态影响。轴面和机械密封面喷有大量的冷却液,轮盘的轴面近似由冷却液的温度(67.5 ℃)决定。

表7 部分进气涡轮机边界条件
3.3 仿真结果分析
3.3.1 涡轮机性能对比
不同喷水量和喷水位置下的涡轮机性能如表8所示。

表8 喷水涡轮的性能对比
由表8中可以看出,喷水冷却会直接影响涡轮机的效率,在径向冷却水量相同的情况下涡轮机的效率随轴向喷水量的增大而减小。5种工况下叶栅进出口的速度三角形如图12所示。图12中,uc为工作叶片平均直径处的圆周速度,c1为工质进口绝对速度,w1为工质进口相对速度,α1为工质绝对进气角,β1为工质相对进气角,c2为工质出口绝对速度,w2为工质出口相对速度,α2为工质绝对出气角,β2为工质相对出气角。5种工况下,工质进出口的绝对、相对速度的大小如表9所示。工况2相比于工况1,进口相对速度减少6.9%,出口相对速度减少8.6%,理想情况下涡轮叶栅进出口的相对速度相等,实际中由于存在漏气损失、轮盘摩擦损失,叶栅出口相对速度会小于进口相对速度,而喷水冷却后转子出口的相对速度相比无冷却更低,说明喷水冷却后的叶栅流道内产生了更多损失。工况3、工况4和工况5的工质进口相对速度分别为916.73 m/s、888.85 m/s和820.21 m/s,出口相对速度分别为731.89 m/s,713.20 m/s和693.70 m/s,由图12可看出这3种工况的相对进、出气角相差不大,而工质进出口的相对速度均随着轴向喷水量的增大而减小,因此随着轴向喷水量的增大,涡轮的功率和效率降低。
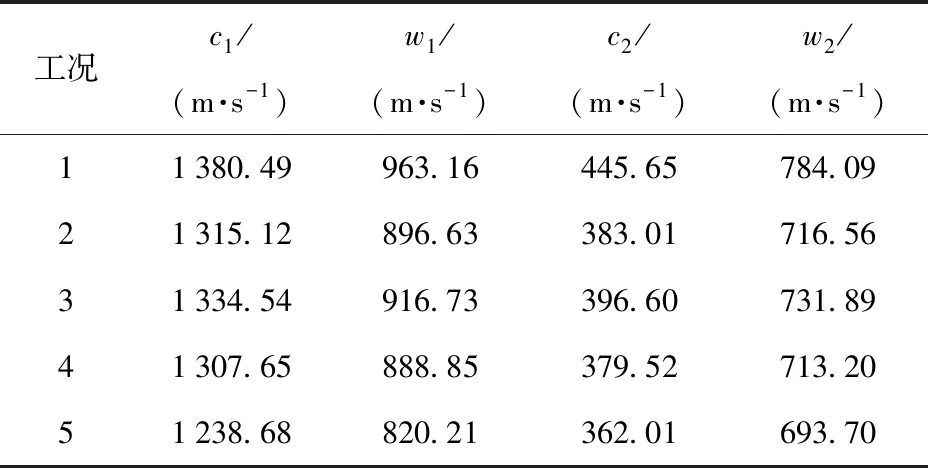
表9 工质进出口的速度

图12 动叶进出口速度三角形
3.3.2 涡轮盘表面温度分布对比
喷水冷却不仅影响涡轮机的性能,还会影响轮盘的温度分布,由于热应力在轮盘总应力中占主导地位[1],而温度分布会直接影响轮盘热应力,本节对涡轮盘温度分布特性着重展开分析。
5种工况下涡轮盘前后表面的温度分布如图13所示,轮盘的温度沿径向方向均匀分布并逐渐增大。工况1中,轮盘前表面的最高温度为1 083.2 K,后表面的最高温度为1 082.8 K;工况2中,涡轮盘前后表面温度有明显降低,前表面最高温度降低到643.7 K,后表面最高温度降低到773.6 K,轮盘温度沿径向方向逐渐增大,并在围带和转子处达到较高温度;在加入径向喷水后,围带的温度有明显降低,但由于液态水难以直接进入转子流道,造成转子处的温度依旧较高。
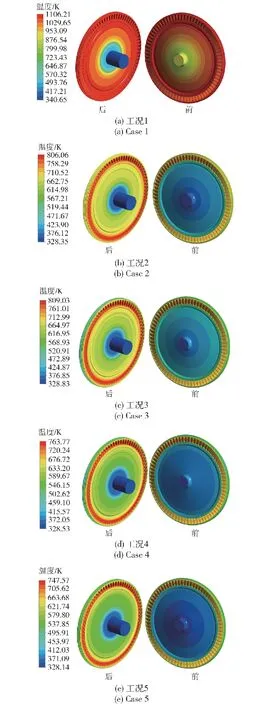
图13 涡轮盘的温度分布
工况1中转子叶栅处的最高温度为 1 102.1 K,主要集中在前缘、流道上端和压力面,吸力面的温度最低,转子处的温度总体相差不大,最大温差为69.3 K;工况2中转子叶栅的最低温度位于叶栅前部,但由于液态水难以进入转子叶片内部(见图14),涡轮叶片大部分依旧被高温燃气加热,叶栅整体上从前到后温度逐渐升高;在加入径向喷水后,由于径向喷水位置在围带中部,转子温度梯度较大的区域在叶片中间部分,在径向喷水量相同的情况下,轮盘的最高温度随轴向喷水量的增大而降低。

图14 工作段转子截面液态水的质量分数
5种工况下轮盘前后表面沿径向方向的温度分布如图15所示,R为除以涡轮半径的无量纲半径。工况1中,轮盘前表面的温度在0.14R处降低,此处轮盘前后表面间的距离变近,使得轮盘前表面的温度更易受到轴面以及机械密封面低温的影响;半径大于0.14R后,高温燃气泄漏速度随半径的增大而增大,导致轮盘前表面温度逐渐升高;半径在0.14R~0.37R时,轮盘后表面受到轴面和机械密封面低温的影响,温度较低;半径大于0.37R后,受高温燃气泄漏的影响,轮盘后表面温度升高。

图15 涡轮盘前后表面沿径向温度分布对比
对比工况2和工况4,加入径向喷水后,轮盘前表面的最高温度降低60.84 K,平均温度降低13.8 K,轮盘后表面的最高温度降低56.47 K,平均温度降低71.8 K,可知径向喷水能够降低轮盘前后表面的最高温度,但对前表面的平均温度影响不大。工况2和工况4的涡轮间隙中液态水的质量分数如图16所示,工况2中轮盘前端间隙中液态水的质量分数约为88%,轮盘背部间隙中液态水的质量分数约为25%,加入径向喷水后(工况4)轮盘前端间隙中液态水的质量分数约为88%,轮盘背部间隙中液态水的质量分数约为35%,故加入径向喷水后轮盘后表面温度降低是由于流入背部间隙的冷却水增多造成的,轮盘后表面的温度降低后通过固体导热影响到了前表面温度。
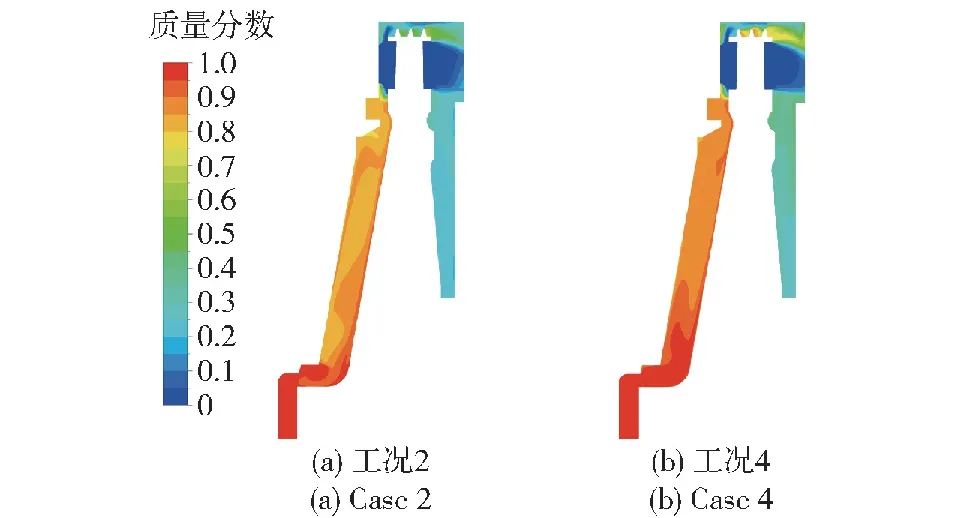
图16 涡轮间隙中液态水的质量分数
对比工况3、工况4和工况5可知,在径向喷水量相同的情况下,轮盘温度的总体趋势保持一致,轮盘前后表面的温度都随轴向喷水量的增大而降低。
3.3.3 热应力热变形分析
将涡轮盘的温度载荷作为有限元计算输入条件,计算轮盘的热应力及热变形,以研究喷水冷却对涡轮盘热应力和热变形分布情况的影响。
不同工况下涡轮盘的热应力分布如图17所示,无冷却时,轮盘的最大热应力位于轮盘轴的根部,为1 291.4 MPa,轮盘轴根部的温度约为500 K,轮盘材料在500 K时的屈服强度约为955 MPa,断裂强度约为1 160 MPa,无冷却时轮盘轴根部的热应力已超过材料的屈服强度和断裂强度。由于轴面喷有大量的冷却水,具有较低的温度(340.65 K),但因轮盘导热导致密封面处具有较高的温度(500 K),使得轮盘轴与轮盘后表面的温度梯度较大,造成轮盘轴根部较高的热应力。
在工况2中,冷却水降低了前表面温度并通过固体导热影响到轮盘后表面以及密封面的温度(360 K),减小了轮盘根部的温度梯度,使得热应力相比无冷却的工况有明显下降。然而工况2中的冷却水主要存在于叶片前缘,导致转子前后缘的温度梯度较高,造成了叶片根部较大的热应力(784 MPa)。 考虑到叶片的最高温度为806 K,轮盘材料在该温度下的屈服强度约为900 MPa,叶片根部的热应力值低于材料的屈服极限,在安全范围内。工况3、工况4和工况5的轮盘热应力分布与工况2相比有所降低,这3种工况下轮盘的最大热应力值分别为772 MPa、750 MPa 和739 MPa,轮盘轴根部的热应力值分别约为430 MPa、370 MPa和350 MPa,均随着轴向喷水量的增大而减小。这3种工况的热应力最大值同样也出现在叶片根部,虽然径向方向上的冷却水能够对叶片顶部进行冷却,但冷却水依旧较难进入叶片流道,造成叶片前后较大的温度梯度。此外,轮盘轴根部的热应力值随着轴向喷水量的增大而减小,这是因为在径向喷水量相同的情况下,轴向喷水量越大,轮盘后表面的温度越低,相应的轮盘后表面与轮盘轴面的温度梯度也越低,轮盘轴根部的热应力值越小。
对比工况2与工况4可知,加入径向喷水后轮盘后表面的热应力有明显降低,径向喷水可对轮盘后表面进行冷却,进而降低轮盘后表面的温度梯度。
5种工况下轮盘前后表面沿径向方向的热应力分布如图18所示,工况1中轮盘前表面除轮盘中心处热应力较低之外,其他位置热应力分布较为均匀,轮盘半径0.14R处的温度梯度较大(见图15(a),导致此处有一热应力的突变;前轮盘半径大于0.14R时,由于燃气泄漏导致温度较高,且温度沿径向方向逐渐增大,对照图15(a)中工况1,当半径大于0.14R时,轮盘的温度梯度较高。加入喷水后,轮盘前表面半径约0.88R时温度梯度较低,热应力较小,当半径大于0.88R后,此处离叶片较近,燃气泄漏量多,温度梯度急剧升高,热应力快速增大,对照图15(a)中的喷水工况,当半径大于0.88R时,轮盘前表面的温度急剧升高,导致此处的温度梯度较大。

图18 涡轮盘前后表面沿径向热应力分布对比
轮盘后表面由于轮盘轴根部的轴面低温,使得轮盘轴根部的温度梯度较大,热应力值较高;而在轮盘后表面半径约0.37R以内,由于泄漏燃气无法流入密封装置,在此半径以内的轮盘温度主要受到固体传热的影响,温度相对于超过0.37R的轮盘后表面温度较低,温度梯度较大,因此在0.37R处轮盘热应力明显升高,在0.43R处达到最大;当后表面半径大于0.43R时,工况1中轮盘后表面热应力降低,对照图15(b)中工况1,轮盘温度趋于平稳,热应力降低;加入喷水后,当后表面半径大于0.43R时,轮盘后表面的热应力先降低后升高,对照图15(b)中的喷水工况,当半径在0.43R~0.76R之间时,轮盘后表面温度随半径变化的温度梯度减小,热应力降低;当半径大于0.76R时,轮盘后表面温度随半径变化的温度梯度增大,热应力升高。
不同工况下轮盘的热变形分布如图19所示,其热变形沿径向均匀分布,并沿径向方向逐渐增大,最大热变形位于围带处。工况1中涡轮盘的最大变形为0.99 mm,工况2中的最大变形为0.83 mm,可见轴向喷水后轮盘的温度降低,最大变形量减小。工况3、工况4和工况5中,由于加入了径向冷却,围带处温度降低,轮盘的最大变形量也相应减小。由于轴向喷水量更大,工况4的最大变形量(0.62 mm)小于工况3的最大变形量(0.76 mm),而工况4 和工况5中的最大变形量相等。

图19 涡轮盘的热变形分布
5种工况下轮盘前后表面沿径向方向的热变形分布如图20所示,加入冷却水后,轮盘前后表面的热变形明显降低。相比工况2,在加入径向冷却后,轮盘热变形进一步降低。加入喷水后轮盘靠近中心处的温度较低,导致有喷水的工况在靠近轮盘中心处的热变形基本相等。在径向冷却水量均为0.1 kg/s的工况下,轴向喷水0.2 kg/s的轮盘前后表面热变形小于轴向喷水0.1 kg/s的轮盘热变形,而轴向喷水0.2 kg/s以及0.3 kg/s这两种工况的轮盘前后表面的热变形几乎一样,说明此时轴向冷却水量对热变形影响不大。

图20 涡轮盘前后表面沿径向热变形分布对比
4 结论
本文对喷水冷却的部分进气轴向涡轮机进行了流-热耦合仿真分析,获得了无冷却以及有冷却时轮盘的温度分布、热应力和热变形。得出主要结论如下:
1)与无冷却涡轮机(工况1)相比,喷水冷却的涡轮机效率降低。加入轴向喷水(工况2)后,涡轮机的效率降低2.8%,同时加入轴向和径向喷水(工况4)后,涡轮机的效率降低3.5%。在径向方向上的喷水量相同(工况3~工况5)时,涡轮机的效率与轴向方向上的冷却水量呈负相关关系。
2)与无冷却涡轮机(工况1)相比,喷水冷却的涡轮机轮盘温度显著降低。轴向喷水冷却(工况2)后,轮盘的最高温度降低27.1%;轴向+径向组合喷水(工况4)情况下,轮盘的最高温度降低30.9%。在径向方向的喷水量相同(工况3~工况5)时,轮盘前后表面的温度与轴向方向上的冷却水量呈负相关关系。
3)喷水冷却措施能够有效地降低轮盘根部处的热应力。轴向喷水冷却(工况2)后,轮盘根部处的热应力降低57.8%;轴向+径向组合喷水(工况4)情况下,轮盘根部处的热应力降低68.8%。在径向方向的喷水量相同(工况3~工况5)时,轮盘前后表面的热应力与轴向方向上的冷却水量呈负相关关系。
4)与无冷却涡轮机(工况1)相比,喷水冷却的涡轮机(工况2~工况5)轮盘的热变形有所降低。轮盘的热变形随径向逐渐增大。在径向方向的喷水量相同(工况3~工况5)时,轮盘前后表面的热变形与轴向方向上的冷却水量呈负相关关系,但当轴向冷却水量达到一定的值后,轮盘的热变形基本不再发生变化。
未来工作将进一步增大喷水量区间,明确喷水量和喷水位置对涡轮机性能的影响规律,得到最优喷水量和最佳喷水位置;考虑涡轮盘的变形对涡轮机性能的影响,最终优化结果可为水下涡轮机的喷水冷却方案提供参考。
