测量不确定度评定方法及在车辆尺寸测量中的应用

陈懿　朱凤华

摘 要：人们对汽车需求量的增长带给汽车行业巨大的机遇和挑战，质量成为汽车产业的生命线，各大车企对与质量相关的检测技术越来越重视，对检测结果的准确度要求越来越高。测量不确定度是对测量结果质量优劣的一种评定，掌握测量不确定度评定的方法，成为检测人员必备的能力，本文对测量不确定度评定的流程和方法进行了总结分析，并以白车身位置误差测量不确定度评定为例进行实际评定操作，为检测工作提供了参考。

关键词：测量不确定度 评定方法 尺寸测量

汽车的需求量的增长来源于经济的飞速发展和人们生活水平的提高，而汽车质量成为人们越来越关注的问题，制造出符合设计质量的汽车是各大车企的使命，而针对汽车质量的检测，其结果的可靠性就显得尤为重要，而各方对在给出的检测结果中提供不确定度的范围也越来越广，但在实际检验工作中，不确定度评定通常由资深检测人员完成，测量不确定度评定的具体操作方法对于一般检测人员来说，还是很难把握，本文对测量不确定度的评定方法进行系统性的阐述，并给出测量不确定度评定实例，旨在帮助检测人员快速掌握并应用测量不确定度。

1 测量不确定度定义

测量不确定度一般用标准偏差或者标准偏差的倍数来表示，通过分析测量不确定度的来源，一般可以找出若干个不确定度分量，部分分量可以通过获得的一系列测量值，用统计分析的方法进行评定，即B类测量不确定度进行评定，而另一部分分量按B类测量不确定度进行评定可以根据经验或其它参考资料获得，再将各不确定度分量进行合成。测量不确定度的大小反应出该次检测结果质量高低，满足客户对不同判定规则的需求。

与测量不确定度相关的概念有A类标准不确定度、B类标准不确定度、合成标准不确定度、扩展不确定度、包含因子等，其关系如下：

2 评定方法

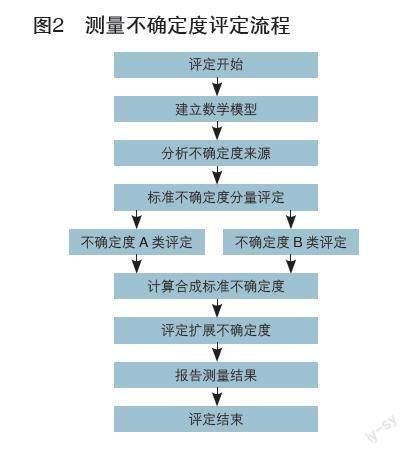
2.1 评定流程，见图2

2.2 建立数学模型

确定被测量Y（输出量）与测量中涉及的所有已知影响量（输入量）X1，X2，……XN间的数学模型：Y=?（X1，X2，……XN）

所有该考虑的影响量都应该在该数学模型中包含有，并且与后面进行不确定度评定时的不确定分量是对应关系。

2.3 不确定度来源

要对被测对象定义有充分的理解，并详细了解与之相关的测量方法、测量仪器、测量条件及测量人员，即从人机料法环五个方面进行具体问题具体分析：

被测对象：定义是否完整、样品稳定性、试验复现性、取样代表性等；

测量方法：从资料中获得的参数的可靠性、测量标准中的方法和测量程序中给出的近似和假设，实施测量的可行性等；

测量仪器：设备计量性能的局限性、设备老化或磨损引起的变化，仪器的校准的不确定度、模拟仪器读数的偏移，标准器和标准物质的可靠性等；

测量条件：环境、温度、空气压力、湿度和其他条件对测量仪器或被测对象的影响，对环境条件测量和控制的完善程度；

测量人员：人员技能，有些测量跟操作人员的技能和判断有关；

2.4 A类标准不确定度评定

A类不确定度分量是根据一组测量值评定的（统计的方法），依据的是既有分布，常用的评定公式有：

2.4.1 贝塞尔公式法

用于测量次数较多的检测（为确保评定可靠，一般测量次数n应不小于10），在测量条件（如测量仪器、检测人员、环境条件、检测方法等）不变的情况下，对被测量X进行n次独立测量，得出一系列测量值：x1、x2……xn

测量值的算术平均值为：

根据贝塞尔公式得测量平均值标准不确定度为：

其自由度ν=n-1，n为测量序列的测量次数。

2.4.2 极差法

用于测量次数较少的检测（测量次数n小于10时，且以n=4～9为宜），在测量条件（如测量仪器、检测人员、环境条件、检测方法等）不变的情况下，对X进行n次独立测量，得出测量结果中的最大值与最小值xmax、xmin。

极差为：

被测量X的A类标准不确定度为：

上式中极差系数C及自由度v与测量次数n关系如下表1所示。

极差法使用起来比较简便，但当数据的概率分布偏离正态分布较大时，应当以贝塞尔公式法的结果为准。

2.4.3 合并樣本标准差

在实际工作中，由于涉及被测样件/点的数量极多，无法在重复性的条件下增加测量次数时，采用贝塞尔公式评定每项测量由于测量重复性引入的不确定度工作量太庞大，如果所用测量仪器持续稳定，可采用合并样本标准差的方法来进行评定。

在测量条件不变的情况下，对每个被测量Xi进行n次独立测量，一共有m个被测量（i=m）。

被测量Xi的A类标准不确定度为：

上式中自由度ν=m（n-1）

2.5 标准不确定度的B类评定

依据已知信息和经验分布进行的评定是B类不确定度评定，B类不确定度的来源主要有仪器设备的使用说明书、计量特性（检定或校准证书提供）、国家标准或技术手册提供的参考数据等。

2.5.1 如输入量X由检定校准证书、设备说明书或其他技术资料给出，则该标准不确定度分量，若证书资料已提供明确的包含因子k值，则可直接计算，若没具体指明K，则可以默认K=2（对应P=95%）；

2.5.2 如根据信息或经验，可明确输入量X的不确定度区间[-a，a]，或误差的范围，则分析输入量X在该区间内的概率分布情况，标准不确定度分量，最常见的概率分布有如下3种：

（1）正态分布：给出输入量估计值及置信区间，即可查表得置信概率和包含因子关系，计算方法：，通常用于在测量条件相同情况下多次测量结果的算术平均值；

（2）均匀分布：测量值均匀分布于上下限之间，计算方法：，通常用于数值修约、测量仪器最大允差等引起的不确定度；

（3）三角分布：测量值出现在区间中心的可能性大于上下限时，计算方法：，如游标卡尺读数的对线误差等。

2.6 计算合成标准不确定度

灵敏系数是判断各不确定度分量对合成不确定度的贡献度，如果某项不确定度分量的灵敏系数是零，则这个不确定度分量对合成不确定度的贡献为零，灵敏一般根据数学模型求偏导得到，即

根据已确定的数学模型Y=?（X1，X2，……Xn），合成标准不确定度为：

Xi，Xj为第i个和第j个分量的估计值且i≠j；

r（xi，xj）为分量Xi、Xj的相关系数；

n为不确定度分量的数量；

如果各不确定度分量之间无相关性，即r（xi，xj）=0，则合成标准不确定度公式可简化为：

如果各不确定度分量对合成不确定度的贡献度相等，也就是灵敏程度一样，即，则合成标准不确定度公式可简化为：

2.7 确定扩展不确定度

被测量可能值包含区间的半宽度就是扩展不确定度，扩展不确定度分为U和Up两种。通常情况下，在报告测量结果时给出扩展不确定度U，即，则测量结果可以表示为：，被测量落在包含区间的概率取决于包含因子k，当数学模型中各不确定度分量间无相关性，且对灵敏度相近或相等时，可认为其符合正态分布，扩展不确定度U的k值可取2，包含区间的包含概率约为95%左右。

2.8 报告测量结果

测量结果应该包含被测量的估计值及其测量不确定度，以及其他相关的信息，报告应尽可能详细，以便使用者可以正确地利用测量结果，常用的表示方式为：

3 白车身位置误差测量不确定度评定

白车身是汽车核心部件之一，其制造质量直接影响其他零部件与之配合，从而影响整车质量。为控制白车身尺寸误差，通常会使用三坐标测量机对白车身孔位测点进行位置检测，查看测点数据是否落在公差范围内。接下来以某白车身测点CCM（02-01L）三坐标位置误差检测测量不确定度评定来展示测量不确定度的评定方法及流程。

3.1 评定方法及数学模型

根据客户提供的测点文件及数模编制进行编程，误差值为设备示值，将得到的误差值与客户提供的测点文件的公差要求进行比较及作出判定。

测量所用设备为海克斯康双臂测量机，型号为HRAVO-HD Image 601625，其测量范围为：6m×3m×2.5m，最双臂最大允许误差为±（38+17L/1000）μm，光栅尺分辨率为0.5μm。

由试验方法和原来，可以得出数学模型为：

式中：lM——坐标值；

L——三坐标读数；

3.2 测量不确定度分量

（1）测量重复性，为获得三坐标测量机测量的重复性，运行已编制完成的检测程序，重复检测10次，以获得测量重复性不确定度分量；

（2）三坐标测量机示值误差，由测量机示值误差带来的不确定度分量；

（3）三坐标测量机分辨率，由标测量机光栅尺分辨率引入的不确定度分量；

（4）测量环境温度，测量环境温度要求为20±4℃，测量过程每1小时记录一次温度，控制最大温度梯度为1℃/h，由测量环境温度偏移引入的测量不确定度分量；

3.3 A类不确定度分量

三坐标测量重复性引入的不确定度分量u1

在各个条件均相同没有改变的情况下，运行检测程序，重复测量10次，测点CCM（02-01L）的位置误差测量结果如下表：

根据公式得出各位置算术平均值为：

由贝塞尔公式计算得A类不确定度分量：

3.4 B类不确定度分量

（1）三坐标测量机示值误差引入的不确定度分量

根据设备出厂证书，该三坐标测量机的最大允许误差±（38+17L/1000）μm，符合均匀分布，选取包含因子k=，则

测试对象在x、y、z的距离L分别为919.9mm、652.99mm、842.17mm，代入公式可得：

（2）三坐标测量机分辨率引入的不确定度分量

根据设备出厂证书，该三坐标测量机光栅尺分辨率为0.5μm，符合均匀分布，选取包含因子k=，则

（3）测量环境温度偏移引入的测量不确定度分量

測量过程控制最大温度梯度为1℃/h，，白车身材料的热膨胀系数为，符合均匀分布，选取包含因子k=，则

测试对象在x、y、z的距离L分别为919.9mm、652.99mm、842.17mm，代入公式可得：

3.5 合成标准不确定度

由数学模型可得灵敏系数：

因此，合成标准不确定度为

可得：

3.6 扩展不确定度

取包含因子K=2，则扩展标准不确定度为：

3.7 报告测量结果

白车身测点CCM（02-01L）三坐标位置误差检测测量结果如下：

4 结语

通过以上内容的整体论述以及应用实例展示，给出测量不确定度评定的一般方法，但做好测量不确定度评定不是件容易的事，需要检测人员在实际工作中对经常使用的标准方法定期进行评定，通过多次实践，不断总结，对相关影响量和不确定度来源有全面的分析，运用不同的方法实施不确定度评定，从而尽可能地提高测量数据的可靠性，提升实验室的技术水平。

参考文献：

[1]田玉华.液相色谱-质谱联用仪信噪比测量结果的不确定度评定[J].计量与测试技术，2013，40（09）：79-80.

[2]王丹，王琦，陈思方.电源端子骚扰电压不确定度评定[J].电子测试，2022，36（12）：50-52+21.