油田分层精细注水管柱的工作特性建模与仿真

王冲　牛绿茵　左信　岳元龙

摘 要 分层注水技术能够有效控制采油井的油水比例，进而提高油田采收率。為了提升精细注水的合格率，研究智能分层注水管柱的工作特性建模方法。首先介绍分层注水的管柱结构，定性分析结构参数改变时各层段注水工作点的变化规律；然后根据管柱结构，基于达西公式、注水泵及配水器水嘴的流量特性，建立分层注水管柱的压力-流量参数工作特性模型，得到不同层注水工作点的求解方法；最后采用数值仿真方法观察分析稳态注水工作点的变化。验证分层注水管注工作特性模型，并通过图像得到：恒压注入和恒流注入模式下，井口阀组和井下水嘴开度改变，将会改变地面向井下解算和从井下向地面解算的压力-流量特性曲线的曲率或截距，进而得到稳态注水工作点变化规律。使两条曲线的交点（即注水稳态工作点）发生变化。

关键词 注水管柱 分层精细注水 工作特性 机理建模 注水合格率 注水工作点

中图分类号 TP273   文献标识码 A   文章编号 1000-3932（2023）04-0521-09

分层注水技术是当今油田开发领域最经济、高效的技术之一。分层注水可以针对不同油层之间的模型差异，分别有效控制各层采油井的油水比例，提高油田整体采收率，对于确保油田高产高效采油，保持油田产量稳定增加，提高油田经济效益具有重要意义。

国外的分层注水工艺相对简单，主要为分层注水完井工艺，大多采用井口流量调节器和井下流量调节器进行定量配水，一般不在井下调节流量，不配套对应井下流量调节设备。而我国的分层精细注水技术，则经历了从固定注水到钢丝打捞、电缆测量和调整注水的技术迭代，在保持高产和提高注水采收率方面，该技术正在发挥重要作用。随着陆上油田进入注水开发后期，油井注采关系相较过去更加复杂，层间差异更为显著，耦合度大幅增加。同时，原油含水率明显增加，水驱效率大幅降低，导致开发成本明显增加。增加分层注水井数、精细注水和高效注水，已经成为提高采收率的3个重要途径。目前，我国的分层精细注水技术与预期目标仍有巨大差距，尤其是在注采关系复杂、层间耦合严重的情况下，分层注水技术不能很好地确保各层油水比例达到最佳，重要原因之一是目前采用的注水管柱建模技术大多采用非机理辨识方法，尚不具备完善的注水管柱动态机理模型。辨识方法建模需要注水管柱的大量测试数据，但是在油田生产过程中，安排测试计划进行数据采集会影响生产，成本很高；其次，辨识方法建模不能得到注水管柱的实际物理模型，相较于机理建模，其鲁棒性往往较差，在模型出现误差后，对于造成误差的原因也更难分析。文献［1］提出一种基于新CISs（水泥完整性模拟器）计算应力状态的注水井水泥分区建模方法，并进行了大规模数据测试，验证了该模型的准确性；文献［2］提供了一种基于隐式压力和显式浓度（IMPEC）的低盐度注水力学建模方法，并使用UTCHEM Iphreeqc软件进行仿真建模，通过该模型解算出了低盐度注水的注水方案；文献［3］提出一种基于斯托克斯动力学公式结合内部渗透和外部渗透的预测注水井吸水率下降局部模型，该模型通过将外部渗透和内部渗透阻力相流动结合，得到注水量的下降规律；文献［4］给出一种在细长裂缝中注水的模型，采用基于伽辽金方法的数值模拟仿真，通过注水实验证明了所提方法的稳定性和准确性；文献［5］提出一种针对复杂三维地图中的流体，基于深度学习的地质参数化建模方法CNN-PCA，通过3种类型的数据集测试，证明了该方法具有较好的鲁棒性。文献［6］使用数据驱动方法对注水井建立了辨识模型，并将该方法在中国东部某油田落地，使该油田的采油率较以前提高了8.2%；文献［7］提出一种在不确定地质条件下，基于CNN网络结构对储油层进行建模的算法，并将该算法与PSO网络结合进行优化，提高了算法的计算效率；文献［8］提出多核学习（MKL）数据驱动方法，并将该方法用于模拟地下储层的多孔性分布，该方法能够有效识别地质特征，并将其输入到储层模型中；文献［9］提出基于挤液扩容水力波及范围的可注性系数和挤液渗透率，推导了单口和两口水平井挤液扩容水力波及范围的解析解，最后应用模型对现场挤液的施工效果进行预测，并利用有限元计算结果证明该解析解的准确性；文献［10］通过注水管柱进行机理建模，对注水井的起始注入压力（FIP）进行预测，通过现场测试证明了预测模型的准确性，并得到了FIP产生变化的原因。

为提升精细注水的合格率，开展智能分层注水管柱的工作特性建模及仿真研究，笔者采用数值仿真方法，定量分析恒压注入和恒流注入模式下，井口阀组和井下水嘴开度改变时注水工作点的迁移规律。

1 分层注水管柱结构

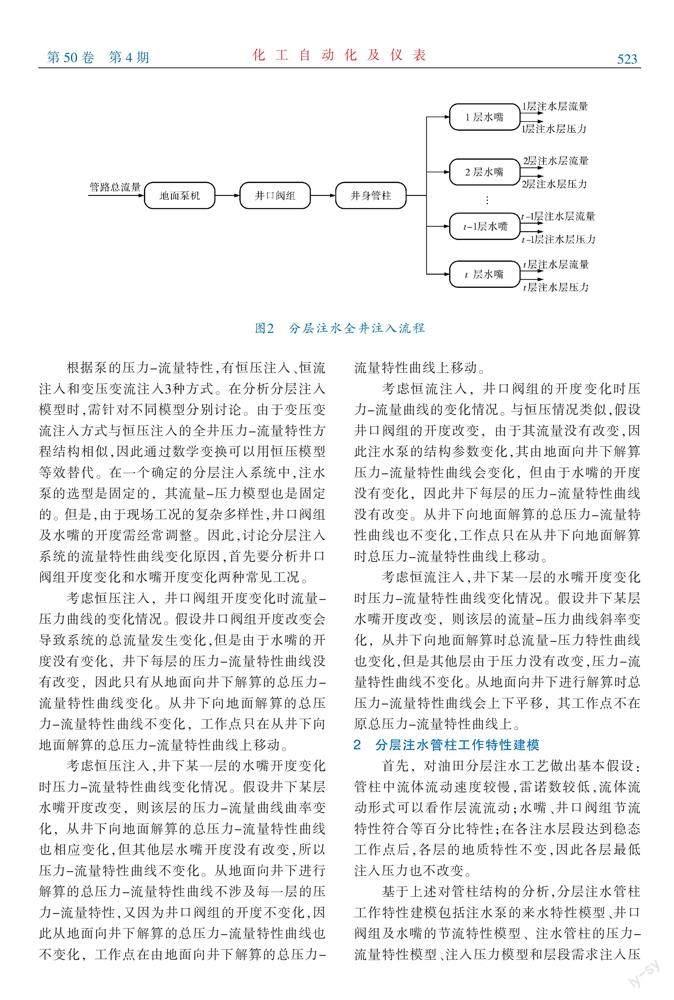
分层注水系统的结构如图1所示，由t个地质特性互异的地层、分层注水管柱及地面监控设备组成，其中注水管柱是实现分层注水功能的核心。

从地面到井下，注水管柱依次包括：注水泵、井口阀组、井口流量变送器、井身管柱、n个井下配水器。注水泵为下游提供高压水介质。井口阀组根据地层注水工作点需求，改变配水压力或流量。井下配水器由控制器、水嘴及电气部件组成，控制器通过控制水嘴开度调节不同层段注入流量或压力。本研究建立的分层注水管柱工作特性模型即压力-流量模型，并拟通过数值仿真方法验证模型的正确性。

分层注水全井的注入流程如图2所示，其中，注水泵的选型需要考虑不同的地质特征及管路模型。

根据泵的压力-流量特性，有恒压注入、恒流注入和变压变流注入3种方式。在分析分层注入模型时，需针对不同模型分别讨论。由于变压变流注入方式与恒压注入的全井压力-流量特性方程结构相似，因此通过数学变换可以用恒压模型等效替代。在一个确定的分层注入系统中，注水泵的选型是固定的，其流量-压力模型也是固定的。但是，由于现场工况的复杂多样性，井口阀组及水嘴的开度需经常调整。因此，讨论分层注入系统的流量特性曲线变化原因，首先要分析井口阀组开度变化和水嘴开度变化两种常见工况。

考虑恒压注入，井口阀组开度变化时流量-压力曲线的变化情况。假设井口阀组开度改變会导致系统的总流量发生变化，但是由于水嘴的开度没有变化，井下每层的压力-流量特性曲线没有改变，因此只有从地面向井下解算的总压力-流量特性曲线变化。从井下向地面解算的总压力-流量特性曲线不变化，工作点只在从井下向地面解算的总压力-流量特性曲线上移动。

考虑恒压注入，井下某一层的水嘴开度变化时压力-流量特性曲线变化情况。假设井下某层水嘴开度改变，则该层的压力-流量曲线曲率变化，从井下向地面解算的总压力-流量特性曲线也相应变化，但其他层水嘴开度没有改变，所以压力-流量特性曲线不变化。从地面向井下进行解算的总压力-流量特性曲线不涉及每一层的压力-流量特性，又因为井口阀组的开度不变化，因此从地面向井下解算的总压力-流量特性曲线也不变化，工作点在由地面向井下解算的总压力-流量特性曲线上移动。

考虑恒流注入，井口阀组的开度变化时压力-流量曲线的变化情况。与恒压情况类似，假设井口阀组的开度改变，由于其流量没有改变，因此注水泵的结构参数变化，其由地面向井下解算压力-流量特性曲线会变化，但由于水嘴的开度没有变化，因此井下每层的压力-流量特性曲线没有改变。从井下向地面解算的总压力-流量特性曲线也不变化，工作点只在从井下向地面解算时总压力-流量特性曲线上移动。

考虑恒流注入，井下某一层的水嘴开度变化时压力-流量特性曲线变化情况。假设井下某层水嘴开度改变，则该层的流量-压力曲线斜率变化，从井下向地面解算时总流量-压力特性曲线也变化，但是其他层由于压力没有改变，压力-流量特性曲线不变化。从地面向井下进行解算时总压力-流量特性曲线会上下平移，其工作点不在原总压力-流量特性曲线上。

2 分层注水管柱工作特性建模

首先，对油田分层注水工艺做出基本假设：管柱中流体流动速度较慢，雷诺数较低，流体流动形式可以看作层流流动；水嘴、井口阀组节流特性符合等百分比特性；在各注水层段达到稳态工作点后，各层的地质特性不变，因此各层最低注入压力也不改变。

基于上述对管柱结构的分析，分层注水管柱工作特性建模包括注水泵的来水特性模型、井口阀组及水嘴的节流特性模型、注水管柱的压力-流量特性模型、注入压力模型和层段需求注入压力模型。联立上述模型方程，可以得到全井的总压力-流量特性模型，进而得到稳态注水工作点的压力-流量特征。

2.1 注水泵的来水特性模型

2.2 井口阀组及水嘴的节流特性模型

2.3 注水管柱压力-流量特性模型

2.4 注入压力模型

2.5 层段需求注入压力模型

2.6 工作点求解

3 工作特性模型仿真

根据第2节的基本假设，管柱中流体速度较慢，可以看作为层流流动，考虑地质条件，会有恒流注入、恒压注入和变流变压注入3种注入方式，其中，变压变流注入可以等效成恒压注入；此外，井口阀组和井下配水器水嘴开度的调整也会改变注水工作点的位置。基于以上两点，设计恒压注入模型仿真和恒流注入模型仿真，并分别分析井口阀组开度改变和配水器水嘴开度改变时，不同层段的注水工作点迁移规律。仿真过程以井下3个注水层段为例，全井地层特性和注水管柱结构采用某油田的实际工程参数（表1、2）。

3.1 恒压注入模型仿真

考虑地质疏松、注水层段中压力损失较快的情况，选择离心泵或泵房进行注水，使管柱中的压力保持恒定。分别考虑井口阀组和配水器水嘴变化的两种情况进行仿真。

图3是恒压模式下改变井口阀组开度，仿真得到的压力-流量关系曲线。其中，向上的曲线表示由井下向地面解算求得的压力-流量关系，绿色、黑色和红色三条曲线分别表示3个注水层的压力-流量关系；粉色曲线表示从井下向地面解算的总压力-流量特性关系。向下的两条曲线表示由地面向井下解算求得的压力-流量关系，深蓝色曲线为地面阀门开度改变前，由地面向井下解算的压力-流量关系；浅蓝色曲线表示地面阀门开度改变后，由地面向井下解算的压力-流量关系。由于不同层段需要满足的注入压力条件不同，因此全井流量-压力曲线在满足不同层段注入压力条件处呈现出分段趋势。图3中由井下向地面解算的压力-流量关系曲线与地面向井下解算的压力-流量关系曲线的交点为稳态注水工作点，满足式（14）。在得到稳态工作点处的压力后，再将该压力值代入各分层流量压力关系曲线，即可解算出全井各层段位于工作点时的压力-流量关系。从图3可以看出，当只改变井口阀组开度，并且注入压力大于各层段的最小注入压力时，井下各注水层段压力不改变，因此，只有由地面向井下解算的总压力-流量特性曲线改变。

图4是恒压模式下改变井下某层段水嘴开度，仿真得到的压力-流量关系曲线。向上的曲线表示由井下向地面解算求得的压力-流量关系，深蓝色、黑色、黄色的曲线表示水嘴开度改变前，各注水层段的压力-流量关系；红色的曲线表示水嘴开度改变后，开度改变层段的压力-流量关系；紫色和浅蓝色的曲线对应阀门开度改变前后，由井下向地面解算的总压力-流量特性。向下的绿色曲线表示由地面向井下解算的总压力-流量特性。图4中，由井下向地面解算的压力-流量关系曲线和地面向井下解算的压力-流量关系曲线的交点为稳态注水工作点。由于地面阀开度固定，因此地面向井下解算的总压力-流量特性曲线不变，单层段配水器水嘴开度变化，引起由井下向地面解算的总压力-流量特性曲线产生变化，同时驱动层段流量与全井开度成正相关关系变化。

3.2 恒流注入模型仿真

考虑注水层段中流量损失较快的情况，选择柱塞泵进行注水，使管柱中的流量保持恒定。分别考虑井口阀组和配水器水嘴开度变化的两种情况进行仿真。

图5是恒流模式下改变井口阀组开度，仿真得到的压力-流量关系曲线。向上的曲线表示由井下向地面解算求得的压力-流量关系，蓝色、黑色和红色3条曲线分别表示3个注水层的压力-流量关系；紫色曲线表示从井下向地面解算的总压力-流量特性关系。两段向下的两条曲线表示由地面向井下解算求得的流量压力关系，绿色曲线为地面阀门开度改变前，由地面向井下解算的压力-流量关系；黄色曲线表示地面阀门开度改变后，由地面向井下解算的压力-流量关系。图5中由井下向地面解算的压力-流量关系曲线和地面向井下解算的压力-流量关系曲线的交点为稳态注水工作点，满足式（14）。井口阀组开度变化，井下配水器水嘴开度和各层段的需求流量不变、注水管柱中的压力变化，从井下向地面解算的总压力-流量曲线不变化，从地面向井下解算的总压力-流量曲线的曲率、截距均变化，各层段压力成负相关关系。

圖6是恒流模式下改变井下某层段水嘴开度，仿真得到的压力-流量关系曲线。向上的曲线表示由井下向地面解算求得的压力-流量关系，深蓝色、黑色、黄色的曲线表示水嘴开度改变前，各注水层段的压力-流量关系，红色的曲线表示水嘴开度改变后，开度改变层段的压力-流量关系；紫色和浅蓝色的曲线表示阀门开度改变前后，由井下向地面解算的总压力-流量特性。向下的绿色和棕色曲线表示水嘴开度改变前后由地面向井下解算的总压力-流量特性。图6中由井下向地面解算的压力-流量关系曲线和地面向井下解算的压力-流量关系曲线的交点为稳态注水工作点。井下配水器某层段水嘴开度改变，井口阀组和其他水嘴开度不改变，开度改变注水层段压力-流量特性曲线变化；其他层段的水嘴开度不变，所以其他层段压力-流量特性曲线不变、从井下向地面解算的总压力-流量特性曲线改变。由于注入方式为恒流注入，管柱中压力变化，从地面向井下解算的总压力-流量特性曲线上下平移。

4 结束语

笔者提出一种油田分层注水管柱的工作特性建模方法。首先对分层注水系统的架构和结构参数改变时各层段注水工作点的变化规律进行定性分析；其次，基于注水泵流量特性、管路摩擦损失、水嘴和阀门的节流特性及达西公式等对管柱工作特性进行机理建模，提出一种求取稳态注水工作点及其迁移规律的方法。最后，针对该模型进行数值仿真，并基于全井压力-流量曲线验证机理分析得到了工作点的迁移规律。

参 考 文 献

［1］ THEROND E，BOIS A P，WHALEY K，et al.Large-Scale Testing and Modeling for Cement Zonal Isolation in Water-Injection Wells［J］.SPE Drilling & Completion，2017，32（4）.DOI：10.2118/181428-PA.

［2］ KORRANI A K N，SEPEHRNOORI K，DELSHAD M.A Novel Mechanistic Approach for Modeling Low Salinity Water Injection［C］// SPE Annual Technical Conference and Exhibition.New Orleans，Louisiana，USA：OnePetro，2013.https：//DOI.org/10.2118/166523-MS.

［3］ PANG S，SHARMA M M.A Model for Predicting Injectivity Decline in Water-Injection Wells［J］.SPE Formation Evaluation，1994，12（3）：194-201.

［4］ KARIMI-FARD M，FIROOZABADI A.Numerical Si-mulation of Water Injection in Fractured Media Using the Discrete-Fracture Model and the Galerkin Method［J］.SPE Reservoir Evaluation & Engineering，2003，6（2）：117-126.

［5］ LIU Y M，DURLOFSKY L J.3D CNN-PCA：A deep-learning-based parameterization for complex geomodels［J］.Computers & Geosciences，2021，148：104676.

［6］ DELI J I A，HE L I U，ZHANG J，et al.Data-driven optimization for fine water injection in a mature oil field［J］.Petroleum Exploration and Development，2020，47（3）：674-682.

［7］ KIM J，YANG H，CHOE J.Robust optimization of the locations and types of multiple wells using CNN based proxy models［J］.Journal of Petroleum Science and Engineering，2020，193（2）：107424.

［8］ DEMYANOV V，BACKHOUSE L，CHRISTIE M.Geological feature selection in reservoir modelling and history matching with Multiple Kernel Learning［J］.Computers & Geosciences，2015，85：16-25.

［9］ GAO Y F，CHEN M，LIN B T，et al.An analytical model for water swept area in SAGD wells［J］.Xinjiang Petroleum Geology，2018，39（2）：1-13.

［10］ LU Y，LI H T，LU C，et al.Predicting the fracture initiation pressure for perforated water injection wells in fossil energy development［J］.International Journal of Hydrogen Energy，2019，44（31）：16257-16270.

（收稿日期：2022-12-15，修回日期：2023-04-27）

Modeling and Simulation of the Working Characteristics of Oilfield Layered Fine Water Injection String

WANG Chong NIU Lv-yin ZUO Xin YUE Yuan-long

（1. CNPC Jidong Oilfield Machinery Company； 2. College of Information Science and Engineering，

China University of Petroleum （Beijing） ）

Abstract   Layered water injection technology can effectively control the oil-water ratio of oil wells and then enhance oilfield recovery efficiency. For purpose of improving the acceptability of fine water injection， a method to model working characteristics of the intelligent layered water injection string was proposed. Firstly， having the water injection string structure of layered water injection introduced and the migrating rule of water injections work points for each layer section qualitatively analyzed while the structural parameters have been changed； secondly， having the proposed structure considered， Darcy-Weisbach formula and flow characteristics of water injection pumps and  nozzles of the the underground water distributor based to establish the working characteristic model of layered water injection string so as to obtain a method for solving different water injection working points in different layers； finally， having  simulation method adopted toverify work points working characteristics model of layered water injection string. The results  through figures show that， under the modes of constant pressure injection and constant current injection， the change of wellhead valves and downhole water nozzles opening will change curvature or intercept of the pressure－flow characteristic curves calculated from the ground to underground and from the underground to ground， and then change the intersection of the two curves （i.e. the steady－state work points of water injection）.

Key words    water injection string， layered fine water injection， working characteristics， mechanism modeling，  water injection acceptability， water injection point