极小样本两独立定量资料假设检验方法比较

郭轶斌，李佳迅，吴 骋，郭 威，何 倩

1.海军军医大学卫生勤务学系军队卫生统计学教研室（上海 200433）

2.海军军医大学基础医学院（上海 200433）

在基础医学实验研究中，研究对象以细胞、动物为主，一些实验细胞或动物模型不仅构造困难，而且花费较大，如巴马小型猪或恒河猴等，不仅动物本身费用较高，同时因伦理限制无法纳入太多。因此，部分动物实验的样本量极小，如每组小于10 例[1-3]。统计学上为了保证一定的统计检验效率，常要求样本例数不能过小。此外，在使用如独立样本t检验等参数检验方法时，还要求样本服从正态分布和方差齐性的假设[4]。但在极小样本的情况下，即使是不服从正态分布的样本，在统计检验效率很低的情况下也无法拒绝H0假设（样本服从正态分布或满足方差齐性）。当独立定量资料样本不满足正态分布或方差齐性假设时，可以使用对数据分布不敏感的非参数检验，对于两组独立定量资料，可以使用Wilcoxon秩和检验或Mann-WhitneyU检验来比较两个样本所代表的总体分布位置是否相同[5-6]。但这两种方法是将样本的原始数据编秩后再进行后续的假设检验，当资料服从参数检验的条件时，会导致样本大量变异的信息损失，进而影响统计检验效率，增加犯Ⅱ类错误的概率[7]。当样本量小于4 时，使用Wilcoxon 秩和检验的P值均大于0.05。Siegel 认为样本量小于6 时，不能使用t检验[8]。祝国强等认为在对非正态极小样本的定量资料进行统计推断时，不适合使用t检验，推荐使用Wilcoxon 秩和检验[9]。林正大等认为在大样本或偏离对称性较远的情况下，Wilcoxon 秩和检验更优[10]。对于统计学的频率学派来说，假设检验和置信区间（Confidence Interval,CI）是一对相伴相随的概念，在同一置信度/检验水准下，参数的置信区间未跨过拒绝域，假设检验则不能拒绝H0。Bootstrap 法是一种可以用来稳健地估计置信区间的非参数方法，其通过对原始样本数据进行有放回抽样得到统计量的经验分布，从而估计统计量对应总体参数的置信区间[11]。在极小样本时，Bootstrap 法能否达到其在大样本中的稳健性，以及该方法估计的置信区间的精度也值得进一步探索。

本研究采用蒙特卡洛数据模拟方法，比较两独立样本t检验、Wilcoxon 秩和检验和Bootstrap 置信区间法在解决极小样本两独立定量资料比较中的表现，以期为相关实验性研究提供方法学参考。

1 资料与方法

1.1 模拟数据的生成

通过蒙特卡洛数据模拟方法生成模拟数据，主要有以下几个模拟情景。样本含量：本研究主要模拟极小样本量下的统计方法表现性能，共模拟5 种样本量——每组各2、3、5、10 和20。均数差：共设置5 种均数差——0、0.5、1、2 和3。从均数相同的两总体中抽样，两总体均数差为0，H0成立，且均数差的置信区间包含0，认为两样本来自同一总体，两组样本均数的不同由抽样误差造成，当统计检验方法拒绝H0时则认为发生I类错误。当两样本均数差不为0 时，两样本不是来自同一样本，若统计检验方法未能拒绝H0，则认为发生Ⅱ类错误。样本分布：共设置3 种总体分布，第1 种为两样本均服从总体方差为12 的正态分布，总体均数根据均数差确定（其中一组为0，即第一组的总体为标准正态分布）；第2种（偏态分布一）为两样本服从偏度系数为1.5，峰度系数为3.0 的偏态分布；第3 种（偏态分布二）为两样本服从偏度系数为1.0，峰度系数为2.0 的偏态分布[12]。

对以上三个因素的不同水平进行全排列构建75 种（5 种样本量×5 种均数差×3 种总体分布）情景，每种生成10 000 个模拟数据集。

1.2 检验方法

基于Bootstrap 法估计均数差的置信区间。采用Bootstrap 重抽样技术对模拟数据集进行1 000次重抽样构建两样本均数差的经验分布。通过估计经验分布的第2.5%和第97.5%分位数确定均数差的95%CI。当95%CI 下限大于0 或上限小于0 时，认为两组均数差异有统计学意义，两样本对应的总体均数不同。

参数和非参数假设检验法。采用两独立样本t检验和Wilcoxon 秩和检验对两总体均数是否相同进行假设检验。与Bootstrap 法估计的95%CI相对应，假设检验的检验水准α=0.05，均为双侧检验。

1.3 评价标准

在均数差为0 时，若t检验和Wilcoxon 秩和检验的P值小于α，或Bootstrap 法估计的均数差95%CI 未跨过0，认为发生I 类错误。在均数差不为0 时，以上情形认为成功检验出统计学差异，即未发生Ⅱ类错误。

分别使用t检验、Wilcoxon秩和检验和Bootstrap 置信区间法对75 种情景下，每种情景的10 000 个模拟数据集进行分析。计算并比较3 种方法在不同数据情景下的I 类错误发生率和100%-Ⅱ类错误发生率（统计效率）。

1.4 统计软件和硬件

本研究使用的统计软件为R 4.1.3，数据模拟的平台为塔式服务器，处理器型号为Intel Xeon Gold 6230，内存为384GB。

2 结果

2.1 I类错误

大样本时I 类错误的发生与样本量无关，其仅与检验水准α 有关，但根据本研究的模拟结果，t检验和Wilcoxon 秩和检验的I 类错误发生率均小于检验水准（图1a 和图1b）。当样本量n=2、n=3 时，Wilcoxon 秩和检验的I 类错误发生率为0。这是由Wilcoxon 秩和检验方法特性造成的[8]。对于t检验来说，极小样本时的I 类错误发生率小于检验水准α，尤其是当数据分布为本研究设定的两种偏态分布时更为明显，这可能与此种情形下不适用t检验有关。但Bootstrap 置信区间法的I 类错误发生率较高，当数据服从正态分布时，I类错误发生率随着样本量的增加而下降，当数据为偏态分布时，I 类错误发生率随着样本量的增加而上升（图1c）。

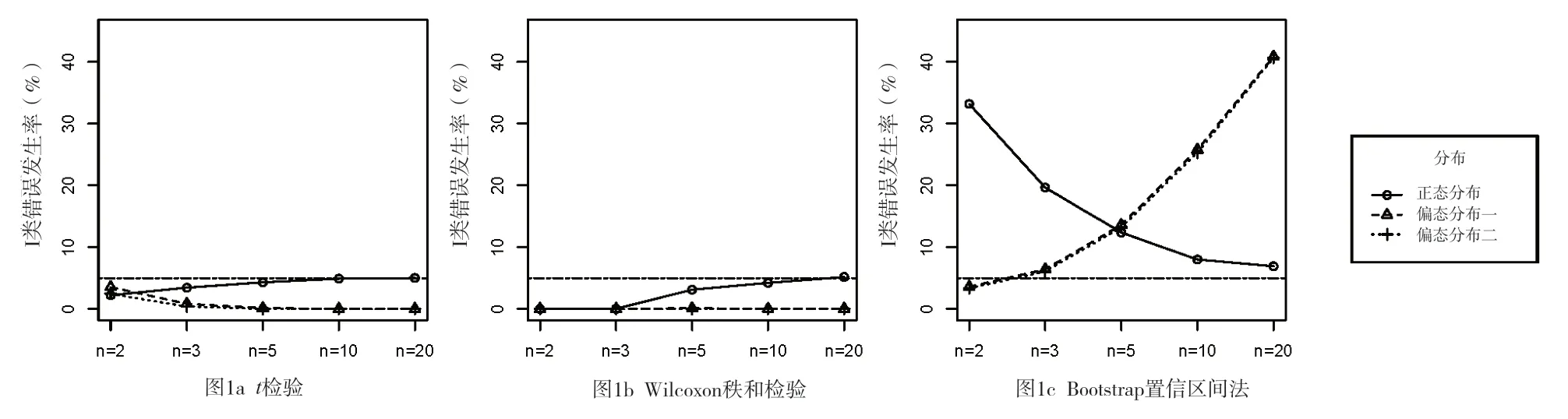
图1 三种方法的I类错误发生率（%）Figure 1.Type I error rate of three methods (%)

2.2 统计效率

三种总体分布下（正态分布、偏态分布一和偏态分布二）分别使用三种方法（t检验、Wilcoxon 秩和检验和Bootstrap 置信区间法）的统计效率分别如图2a、图2b 和图2c 所示。当均数差较小时，无论使用哪种方法，统计效率都很低，Bootstrap 置信区间法表现略优于另外两种假设检验的方法；当均数差较大时，即使样本量很小，Bootstrap 置信区间法仍有较高的统计效率，说明此时犯Ⅱ类错误的概率较低（图2c）。

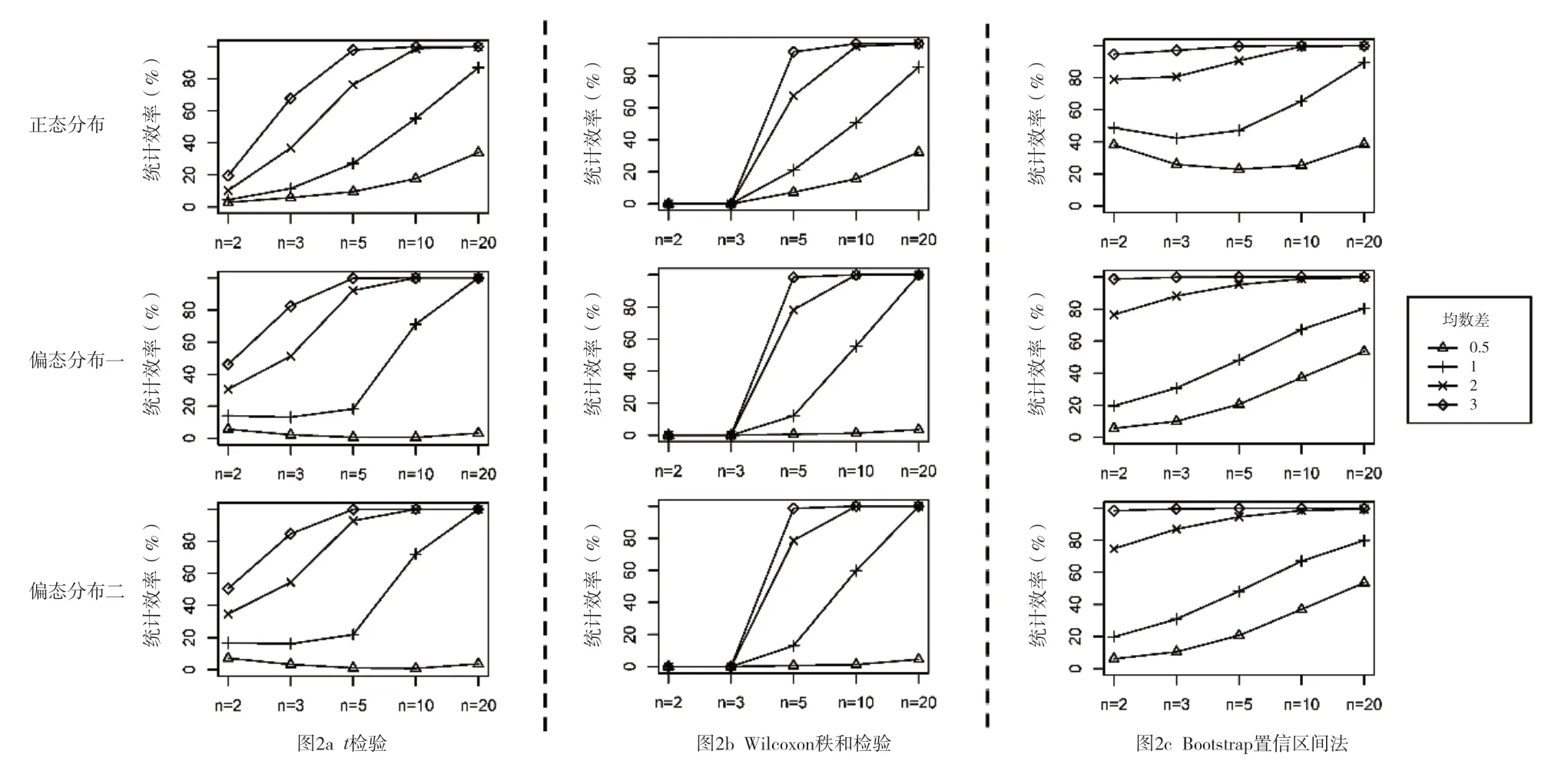
图2 不同情形下三种方法的统计效率（%）Figure 2.Power of three methods in different scenarios (%)

无论数据是否服从正态分布，当样本量极小时（n=2、n=3），t检验的表现优于Wilcoxon 秩和检验。但当样本量较大且均数差也较大时，t检验与Wilcoxon 秩和检验统计效率差异不大（图2a、图2b）。

3 结论

本研究通过数据模拟的方法，探索了采用两独立样本t检验、Wilcoxon 秩和检验和Bootstrap置信区间法对极小样本两独立定量资料进行统计推断时统计效率的差异。由模拟结果可见，相较于Wilcoxon 秩和检验，t检验在样本量极小时（n=2、n=3）仍有一定的统计效率，且对总体数据分布不是很敏感。当数据服从本研究设定的两种偏态分布时，t检验的表现不差于Wilcoxon 秩和检验。在样本量极小时，Bootstrap 置信区间法可以增加统计效率，但在两组样本均数差为0（即两组样本来自同一总体），且数据服从正态分布时，犯I 类错误的概率较高。

综上，根据本模拟研究结果，当数据服从正态分布时，建议使用t检验对极小样本进行统计推断；当数据不服从正态分布时，建议使用Bootstrap 置信区间法对极小样本进行统计推断。由于对于极小样本统计效率太低，当样本量极小时，无论数据服从何种分布，均不建议使用Wilcoxon 秩和检验进行统计推断。