小学数学数形结合教学策略
2023-08-05黄挺艳
文 /黄挺艳
数学思想方法包括数形结合、转化思想、分类思想等。其中,数形结合是学生转化数量关系、空间形式,灵活解决问题的思想方法[1]。众所周知,数与形是数学知识的两种重要的表征方式。数包括数字、算式、定理、概念等,形包括图像、实物、模型等。结合数与形,可以化抽象为直观,化抽象为具体[2]。如此一来,数学学习难度大大降低,学生会充分发挥形象思维作用,探究、掌握数学知识、数学技能,获取数学思想方法,积累活动经验,增强数学学习效果。
一、课前预习阶段:布置数形结合任务,自主学习
预习是学生在学习任务的驱动下,自觉参与的学习活动。数形结合任务是以数学新知内容为基础,以数形结合思想方法为重点的任务。在此任务的作用下,学生会发挥自主性,迁移数学认知,应用数形结合思想方法解决问题,初步建构数学认知,同时掌握数形结合思想方法,夯实课堂学习基础。在实施数形结合教学时,教师可以给学生布置数形结合任务,启发他们自主学习。在任务的推动下,学生进行回想、解题、阅读、操作、反思,实现自主学习。学生积极探究新知内容,建立初步认知,为进行课堂学习做好准备,同时,强化了数形结合意识,提高了数学学习效率。
二、课中讲解阶段:组织数形结合活动,探究新知
(一)围绕基础知识,组织数形结合活动
在学习数学知识时,学生如果能灵活转化数与形,就可以化抽象为直观,轻松地建构认知。在数学课堂上,教师要围绕基础知识,组织数形结合教学活动。
以“两位数加两位数(不进位)”为例,本节课的重点内容是不进位两位数加法的算理。教师先出示加法算式“35+2”,引导学生进行口算。此时,学生迁移已有认知,认真计算。接着,学生毛遂自荐,描述口算过程。有的学生描述道:“35 是3 个十和5 个一。5 个一加2 个一,一共得到7 个一。3 个十加7 个一,得到37。”在学生描述后,教师鼓励他们拿出学具小棒和小组成员合作摆放。在摆放时,大部分学生依据口算过程,移动小棒,如先将5 根小棒和2 根小棒放在一起。教师就此提问:“为什么要先将5 根小棒和2 根小棒放在一起?”学生联想操作过程,踊跃作答:“因为这些都是1 根1 根独立的小棒,不是1 捆小棒。”教师肯定学生的说法,并在黑板上进行竖式运算。在书写出35后,教师发问:“要将2 写在哪里?”学生再次联想操作过程,给出答案:“2 要写在5 下面。”教师及时追问:“为什么要写在5 下面?可以写在3 下面吗?”同时,教师提出任务:“如果将2写在3下面,会出现什么情况?请操作数学小棒,说明其中的道理。”学生认真操作、思考,得出结论。有的学生提道:“2 和5 一样,都表示根数。3 表示的是捆数。”
在如此活动中,学生根据要求,灵活操作数学小棒,轻松地认识算理、算法——当两位数相加时,要先对齐个位,将个位上的数字加在一起。同时,学生在操作的过程中,感受到了数与形之间的关系,增强了数形结合意识。
(二)围绕数学练习,组织数形结合活动
数学练习是解决数学问题的活动,数形结合思想方法是学生解决数学问题的“工具”。数学练习过程正是学生应用数形结合思想方法,解决数学问题的过程。在数学课堂上,教师要围绕数学练习,组织数形结合活动。
以“倍的认识”为例,在课堂上,学生体验了画线段图的活动,解决了数学问题,了解了“倍”的含义,能用线段图解决“一个数的几倍是多少”的问题。立足学生的学习情况,教师呈现练习题:“一支铅笔6 元,一个订书器的价格是一支铅笔的4 倍。请问,一个订书器的价格是多少?”与此同时,教师提出要求:“请分析问题条件,绘制线段图,展现铅笔和订书器价格之间的关系,计算出订书器的价格。”在如此要求的作用下,学生分析问题及条件,把握关键信息,迁移数形结合经验,绘制线段图(如图1)。
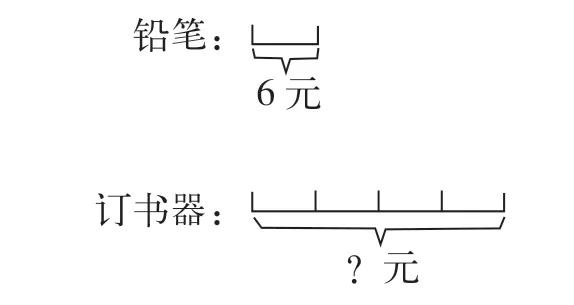
图1
在线段图的助力下,学生轻松地发现铅笔和订书器之间的关系,由此列出算式,认真运算,得出结果。学生通过绘制线段图,直观地把握了数与数之间的关系,由此列出算式,计算出结果,完成了练习任务。
三、课后作业阶段:设计数形结合作业,解决问题
数形结合作业是指应用数形结合思想,解决数学问题的作业,能帮助学生使用适宜的数学思想和知识,灵活解决问题,锻炼问题解决能力。对此,在课后作业阶段,教师可以依据学生的学习情况,设计数形结合作业。
以“植树问题”为例,通过体验课堂教学活动,学生了解了一端植树问题、两端植树问题等,同时积累了数形结合经验。但是,在认知差异的影响下,学生的学习情况不尽相同。对此,在课后作业阶段,教师可设计分层作业(见表1)。
在完成作业时,学生依据自身认知情况,自选题目。面对不同的题目,学生迁移课堂认知,分析题目,把握关键信息,并绘制线段图,运用数形结合方法解决了问题,巩固了课堂所学,同时也锻炼了问题解决能力。
四、结束语
在实施小学数学教学时,教师要紧扣数与形的关系,将数形结合思想方法作为教学工具,依据教学需要,将此方法灵活渗透于不同教学阶段,促使学生运用数形结合思想解决问题,理解数学知识,掌握数形结合思想方法,积累活动经验,提高学习效率。
