变式训练教学模式在高中数学解题中的运用
2023-08-04吉林师范大学数学与计算机学院丰秀悦
吉林师范大学数学与计算机学院 丰秀悦
变式训练教学通过对题型的多种变化和灵活的解题方式可显著提高高中数学教学的趣味性,充分挖掘学生潜能,培养学生发散式思维,从而促进学生对数学知识的多维度理解与运用.因此,为全面提高高中数学学习效率,规避“题海战术”产生的弊端,应进一步研究高中数学解题环节中变式训练教学的具体教学策略,以及在不同题型中的应用要点,帮助学生达到事半功倍的学习效果.
1 变式训练在高中数学解题教学中的应用价值
1.1 提高学生数学学习的效率
在高中数学解题教学中巧妙运用变式训练有助于提高数学学习的灵活性,从而提升学生在数学课堂的学习效率.在高中数学不同教学阶段开展变式训练教学,首先可为学生营造轻松、高效的数学课堂学习氛围,帮助学生掌握多种解题技巧与方法.其次,可通过知识的灵活运用节省教学时间,将更多时间留给学生充分思考或探讨,增强学生学习数学的主观能动性.最后,教师亦可借此途径引导学生对相同知识点所考查的不同题型进行分类总结,促进变式题与母题的融合,为日后的复习打下基础,提高学生综合学习能力.
1.2 激发学生的创新思维
当前,社会各行业竞争十分激烈,通过变式训练培养学生的创新性思维,为国家输送创新型人才应成为学校教学工作的重中之重.因此,学校要求教师在数学教学中着重锻炼学生的变式思维.教师首先需具备创新意识,在具体解题过程中充分发挥个人想象力,对题目进行科学分析、合理变式,尝试利用多种途径解题,针对不同学生的接受能力展开不同角度的讲解,根据学生的反馈对变式方法进行归纳总结,达到多维度激发学生创新思维的效果.此种变式训练方法具有高效性和新颖性,可帮助学生在短时间内发现解答数学问题的思路,扩宽思考数学问题的广度,逐渐形成数学教学的良性循环.
2 变式训练教学在高中数学解题中的运用策略
2.1 类比变式教学策略
类比变式包括解题思路和解题方法的类比,即在某一典型数学问题的解题过程中总结出此类问题的解答思路及方法,运用此种思路同样可解答与之类似的一类数学问题.教师在设计教学方案时,可以将各阶段重要考点分类汇总,选取某一典型例题作为母题,结合该母题采用类比变式,设计出若干变式题目供学生进一步练习,以达到熟练运用该解题思路或方法的目的.
2.2 逆向变式教学策略
高中数学传统课堂教学中,学生多以正向思维解题,但在长时间的数学学习和大量的习题练习后逐渐形成思维定式,如解题思路单一、解题方法缺少灵活性等.因此,教师在课堂教学中应了解培养学生逆向思维的重要性,通过逆向思维帮助学生从另一个角度理解某个定理、数学概念或知识点.这要求教师在日常教学中为学生设计逆向变式问题,引导学生思考并尝试解题.例如,代数运算、不等式性质和几何问题的逻辑推导等方面的题均涉及逆向思维,学生利用逆向思维解决上述问题能提升其推理能力.
2.3 变设问、变条件的教学策略
针对某个数学问题,灵活改变设问方式或命题条件是当前高中数学变式教学最常见的方式,亦是教师在教学初期运用最多的教学方式.鉴于高中数学的整体难度和各学段教学任务,解题教学仅停留在数学问题的表面或只是记忆基本知识点是远远不够的.数学教师应对教材内容进行系统梳理,从多个角度对数学问题展开思考和论证.如,对概念的解析,可针对该知识点设置相应的问题情境,构造同一问题的多种解决方式引导学生深入理解和掌握知识点,进而改变设问方式或问题条件,锻炼学生“举一反三”的能力.
3 变式训练在高中数学教学中的具体运用
3.1 变式训练在函数问题中的运用
高中数学中变式训练教学的具体运用,教师可从函数问题开始,将变式训练融入到函数解题中,引导学生对题目涉及的知识点展开探讨,加强对函数知识的分析及应用能力,积累函数解题技巧和经验,为高中数学函数板块的学习打下良好基础.
A.(1,+∞) B.(2,+∞) C.(-∞,2) D.(1,3)
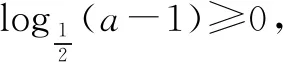
针对该知识点可进一步变换题型,如:
此题与例题1联系紧密,均考查学生对函数定义域应用的熟练程度,且此题增加了对复合函数增减性的考查.因此,学生首先应求出该函数的定义域,然后根据“同增异减”原则,求得单调递减区间.经分析可得,该函数定义域为(-∞,1)∪(2,+∞).令t(a)=a2-3a+2,则函数t(a)在(-∞,1)上单调递减,在(2,+∞)上单调递增.根据复合函数的同增异减性,最终得到所求的单调递减区间为(2,+∞).
上述两道数学题均考查了函数的定义域,而变型题则是对知识点的进一步延伸.此种变式训练有助于学生对函数知识更加熟练的掌握,同时也有助于增强学生深入思考的能力.
3.2 变式训练在几何问题中的运用
几何问题是高中数学的重点、难点,要求学生具备一定的空间想象力.运用变式训练教学,可有效降低几何问题的难度,进而以题目的灵活变换充分锻炼学生的解题思维.
例2某几何体的三视图如图1所示,试用斜二测画法画出它的直观图.
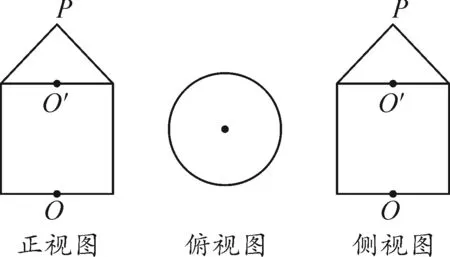
图1
此题考查学生对几何知识的基本掌握能力.根据给定条件不难画出几何体,该几何体直观图如图2所示.

图2
教师通过该题目带领学生温习相关几何知识,可以此为基础继续变式,如:
某几何体的三视图如图3所示,试求其表面积与体积.
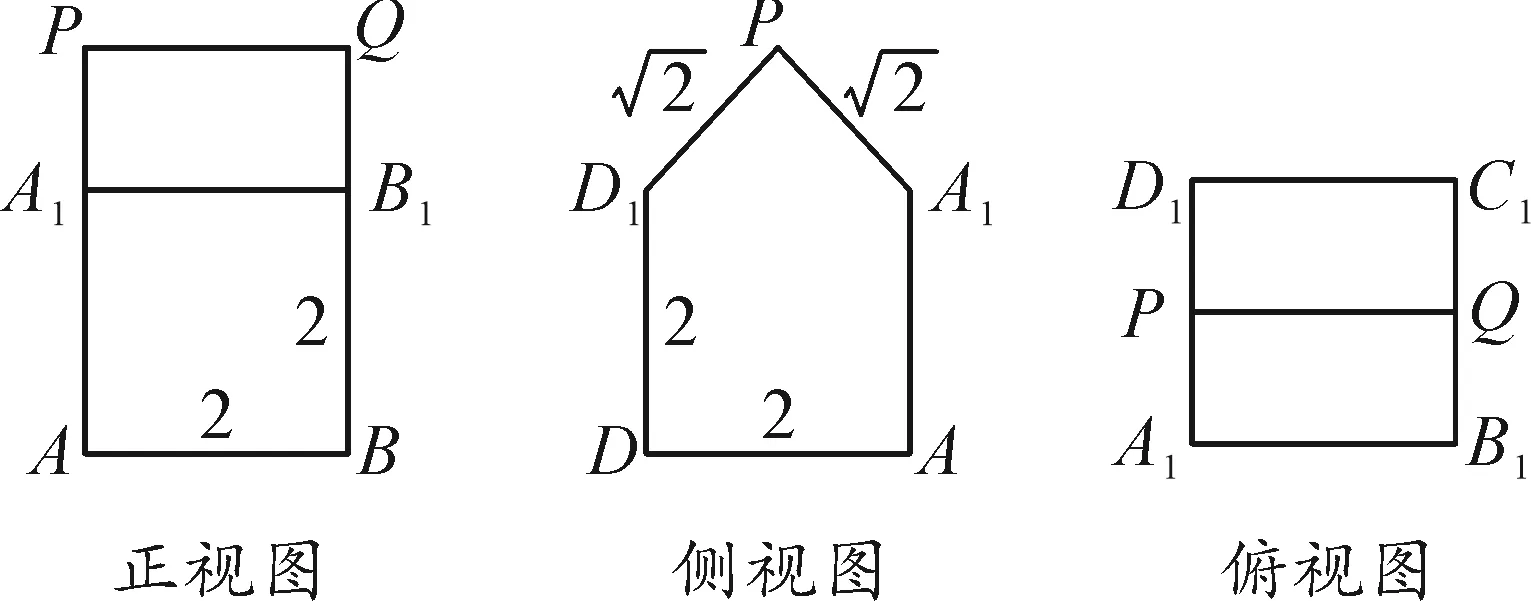
图3
与例2相比,此题抽象性更强,学生可先在头脑中构建出该几何体,然后作答.
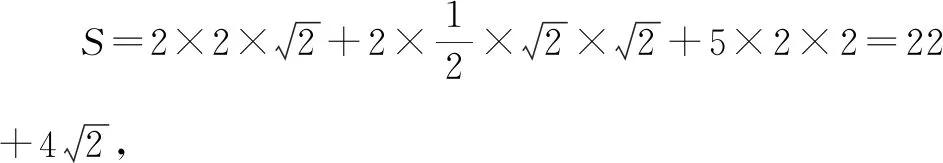
通过以上变式训练,可帮助学生了解立体几何问题的变式方法,从而积累几何问题作答经验.
将变式训练应用于高中数学教学中,可有效激发学生的数学思维,减少不必要的练习,更有利于真正落实“双减”.因此,教师在教学中应注意变式教学方法的使用,充分发挥类比变式、逆向变式以及变设问、变条件等策略的作用,提升学生类比推理能力及归纳总结能力,促使学生掌握多元化的解题方式,增强学生学习数学的信心,全面提升数学素养.
