重视多维切入 打造优质课堂
2023-08-04宁夏回族自治区彭阳县彭阳三中韩占珍
宁夏回族自治区彭阳县彭阳三中 韩占珍
在教学中,有的学生反映“教师讲的能听得懂,但是到自己做的时候就不知从何入手”,也有的学生反映“能看懂教材内容,根据题目解析知晓解题方法,但是到自己独立解题时就不会了”,还有的学生说“有些题目明明做过,当时也做对了,但是过一段时间再做却不会了”.面对这些情况,学生表现得很迷茫、很无奈.其实,很多教师也有同样的无奈,很多题目明明练习过、讲评过且课后也利用变式问题强化过,但是学生的错误率依然居高不下.那么,是什么原因造成学生的迷茫和教师的无奈呢?笔者认为,出现以上现象的根本原因就是学生的“学”一直处于被动的接受状态.学生在学习时习惯于记忆和模仿,很少主动去思考、探索,个人的潜能并没有得到释放,使得自身的“学”一直处于比较浅层的理解和记忆上,并未有效地提高学习能力和思维水平,从而影响了学习的信心,限制了思维的发展.为了改变这一现状,教师在讲解过程中要注重引导学生多维切入,从不同角度、不同维度去思考和解决问题,重视学生的思维训练,这样不仅能够提高学生参与课堂的积极性,而且可以诱发学生思考,释放学生潜能,让数学课堂变得富有生机和活力[1].
笔者以“隐形圆”一课为例,通过“一题多解”凸显多维切入的作用,让学生的学习能力和思维能力落地生根,让学生的核心素养落地生花,完美绽放.
1 教学简录
1.1 情境导入
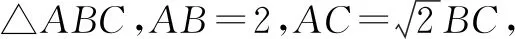
例1属于三角形边角关系问题,主要考查学生数形结合、转化化归思想.本题有一定难度,对学生逻辑推理、数学运算、直观想象等能力提出了较高的要求.问题给出后,教师让学生自行研究,并鼓励学生尝试应用不同的方法解决问题.从学生的练习反馈来看,仅有较少的学生在规定的时间内给出了准确的答案,大多学生则陷入了复杂的运算而难以自拔,可见学生所选择的解题切入点有待商榷,有必要进行优化.
1.2 多维切入
笔者发现,在解题时,学生选择的解题路径具有高度的相似性,他们大多将目光聚焦在边的比例上,尝试利用三角形面积公式找到面积函数解析式,然后利用求函数最大值的思路求解.基于此,教师从学生的视角出发,逐层地引导和启发,让学生发现其他的切入点,以此优化解题策略,提高解题效率.
(1)用数学的思维去思考
师:在解题时大多数同学选择利用三角形面积公式获得函数关系,寻求解决问题的方法,谁来分享一下你的求解过程.(教师让学生板书求解过程.)
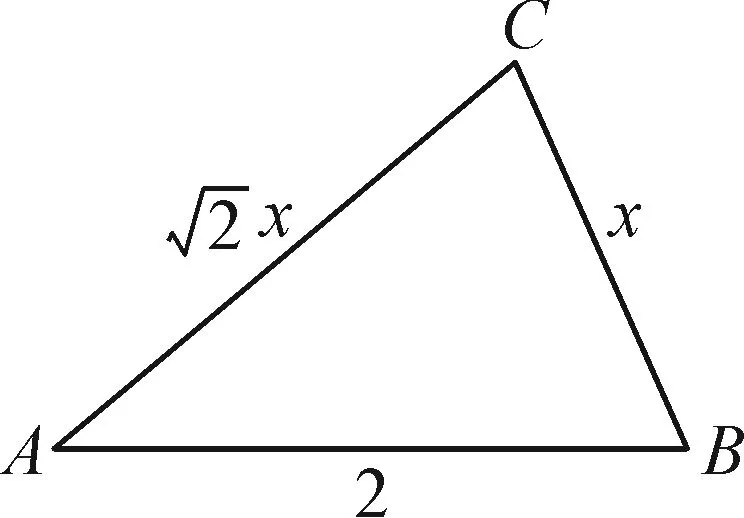
图1
由余弦定理,得
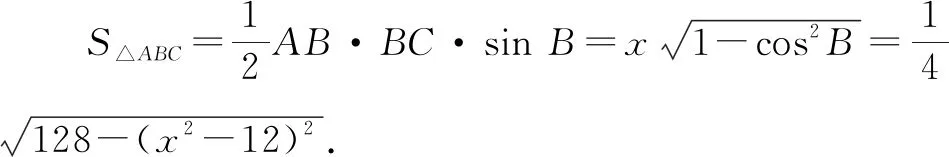
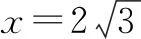
师:很好,很多同学应用了同样的思路,不过有的同学并没有得到答案.解题时,你们遇到的最大障碍是什么?
生齐声:运算.
师:确实,该方法利用余弦定理和面积公式虽然很容易构建出函数关系,但是对运算能力的要求较高,很多同学因为运算复杂而望而止步.课下请大家将运算进行到底,这里不作重点讲解了.
(2)用数学的语言去表达
师:对于AC和BC的比例关系,若从“数量”入手,是否有其他发现呢?
生2:如图2,以AB所在的直线为x轴,以线段AB的中点为坐标原点,建立平面直角坐标系xOy,则A(-1,0),B(1,0).

图2
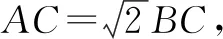
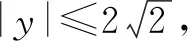
在教师的启发和引导下,学生从另一维度探寻数量之间的关系,将几何关系代数化,建构了更加理想的模型,优化了运算过程.探究至此,很多学生认为已经找到了最优方案,但是教师引入该题的目的并不局限于此,于是继续启发,让学生从另外一个维度继续探寻数量之间的关系.
(3)用数学的眼光去观察
师:刚刚我们利用代数法解决了问题,如果将“数”与“形”结合在一起,你又有什么发现呢?
在该环节,教师鼓励学生进行小组交流与探究,让学生结合生2的解题过程,寻找更为熟悉的几何关系,让学生发现“隐形圆”,以此优化解题过程,提高学生观察、创造能力.经过充分的思考和交流,学生给出了第三种解题方案.
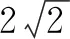
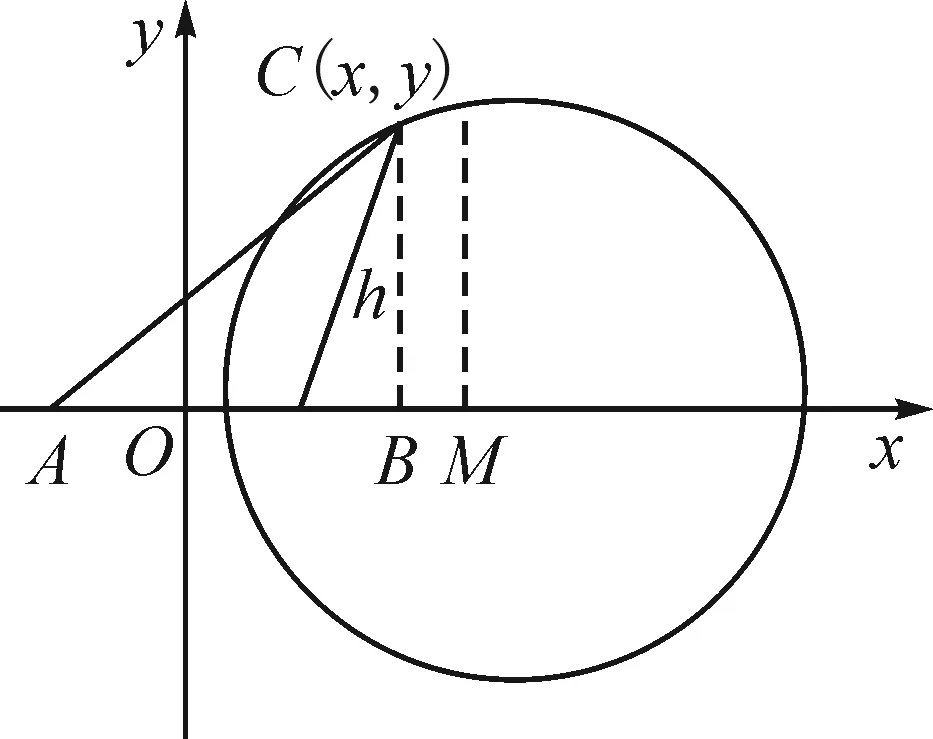
图3
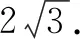
可见,将数学表达式变形后,学生易于发现“圆”的身影,进而将代数问题几何化,运用几何关系解决了问题.这样,将“数”与“形”结合在一起,优化了解题过程,帮助学生积累了丰富的解题经验,有效地发展了学生的思维能力.
教学中,教师引导学生充分挖掘题目的内涵和外延,从不同维度思考并解决问题,既可以让学生发现自身存在的问题,又可以有效地发展思维能力,让学生的认知结构在多维探究中得到了完善和升华.
2 教学思考
对于同一个问题,若选择的切入点不同,则其解题过程也会有所不同.为了提高学生的解题效率,在日常教学中,教师要引导学生多角度、全方位地思考问题,探寻解决问题的不同切入点,以此优化解题过程,发展数学学习能力.
2.1 学会用学生的眼光看问题
教师和学生的知识储备、思维方式存在着较大的差异,因此教师不要将自己的经验强加给学生,要学会从学生的视角去看待问题,这样可以充分地了解学生之所想、之所惑,从而通过有针对性的引导帮助学生解决问题,提高教学有效性.
2.2 关注学生主体作用的激发
我们知道,再生动的讲解若没有学生的参与它也是苍白的、无力的,无法提高学生的学习能力.因此在教学中,教师要学会放手,将探究的主动权交给学生,重视呈现学生的思维过程,充分激发学生潜能,让学生学会思考,学会学习.在教学中,教师要以学生的实际情况为出发点,巧妙设计教学情境,引导学生去思考、去探索、去创新,提升学习品质.
2.3 重视多维切入的培养
多维切入为学生提供了更广阔的视角去思考问题、理解问题,为学生提供了更多、更有效的方法去分析问题、解决问题,其有利于提高学生的“四能”.对于不同的学生,他们思考问题的方式会有所不同,因此在解题时会选择不同的切入点,进而发现不同的解决问题的方法.在教学中,教师要充分发挥个体差异的优势,鼓励学生尝试寻找不同的切入点解决问题,以此帮助学生积累解题经验,打破“懂而不会”“会而不通”的局面,让学生核心素养落地开花.
总之,在教学中,教师要认真设计教学活动,引导学生从不同维度理解问题,利用不同的方法解决问题,以此发展学生关键能力,提高学生数学素养,打造生本高效课堂.
