HPM视角下谈对数的起源
2023-08-04广东省中山市龙山中学
广东省中山市龙山中学 陈 玉 彭 砚
HPM 全称为“History and Pedagogy of Mathematics”,意思是在数学教学中融入数学史,用数学史的教育功能,全面发展学生的数学素养.了解知识的发生、发展过程,对学生数学能力的培养能起到很重要的作用.
但HPM在中学数学教学中一直处于”高评价,低应用”的尴尬位置,知网上有很多数学史在实践中的应用这类型的论文,但在课堂中的应用情况还有待考察.
笔者从各种途径收集了关于对数起源的历史材料,并根据自己的理解进行梳理,然后用HPM方法中的顺应式对对数概念的教学进行深入浅出的教学设计,从学生容易理解的角度对历史材料进行改编.
1 历史材料
关于对数的起源历史材料有很多,最著名的就是以下两个问题.材料1——布拉赫的困扰是对数起源的最根本原因:用来解决计算量大的问题.材料2——纳皮尔的对数是公认的对数起源的过程:纳皮尔对数的发现,实际上是参数方程的化简过程.
1.1 布拉赫的困扰
第谷·布拉赫是16世纪下半叶丹麦的一位天文学家,他的主要研究工作是进行大量精密的天文观测,以便为航海的人们确定船只的位置.在观测后会得到很多数据,这些数据通常是杂乱无章的,处理数据就成了他最头疼的一件事情.比如,下面是他要处理的几个运算:
(1)32×1 024; (2)8 192÷32;
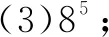
前面三个很容易,是我们熟悉的四则运算,第四个就不那个好算.按我们现在的知识,用笔算开平方其实也能算,但在以前是没有这样的知识的.
事实上,即使是常规的加减乘除与乘方运算,但如果要计算的数值很大,花费的时间就要增加,运算也会变得枯燥无味.距今三百多年前,十六七世纪的数学家经常要进行大量的关于天文和航海数据的计算,如299 792.468×31 536 000,其中,299 792.468是光在真空中的速度 (单位:km/s),31 536 000是一年的总秒数,显然这个计算更加麻烦.
1.2 纳皮尔的对数
假设在一次运动中,有两个沿两条线运动的质点.
如图1,假设AB的长度为107单位,CD无限长,点P从点A向点B运动,同时点Q从点C向点D运动.点P的初速度为107,设PB=x(t),在运动的过程中,点P的速度与x(t)成正比,设比例系数为1,点P的速度为x(t).点Q做匀速直线运动,速度为107.设CQ=y.这是纳皮尔构造的一个几何模型.
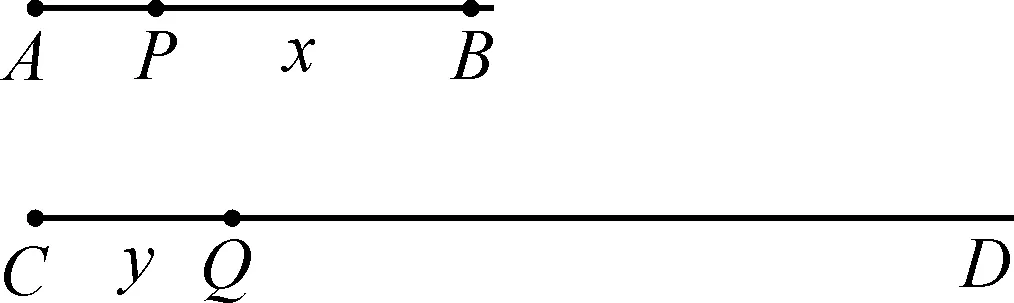
图1
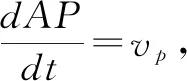
解得x(t)=C·e-t.当t=0时,x(0)=107,代入得C=107.因此有x(t)=107e-t.
而点Q在射线CD上做匀速直线运动,则y(t)=107t.将y定义为x的对数,有y=Nap logx.
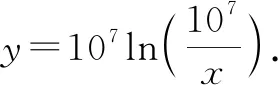
之后,纳皮尔就用这个定义编制出了对数表,虽然花了大量的时间,但是在数学运算上取得了很大的进步.不过,刚开始时纳皮尔选用的底数是一个相对较为复杂的数,并不好用.后来英国数学家布里格斯专程拜访了纳皮尔,并建议将底数改为10,因为这更加符合人们使用十进制的习惯.所以纳皮尔又花了很多时间编制以10为底的对数表格,终于在1617年完成.人们一直都用这样的对数表格进行各种各样的复杂计算.
2 “对数概念的引入”教学设计与实施
2.1 教学分析
(1)教学背景.对数的引入是高中数学的一个难点,大部分学生对于对数的理解有很大的困难.HPM的提出和发展给了高中教师一个新的突破口,一种新的教学方法.课本中都是从指数的问题去引出对数,但从历史上来看,对数的发明比指数要早.从上文可以看出,只要设计合理,让学生了解知识的发生、发展过程,对学生的认知发展有非常大的帮助.
(2)学情分析.“对数的概念”是 2022年人教版必修第一册第四章第三小节第一课时的内容, 在此之前学生已经学习了指数和指数函数,对指数的运算方法也有所了解.本节课的内容既有利于学生对指数有关知识的复习,也有利于对数的运算和对数函数的学习.学生在追根溯源的过程中体会数学史的魅力,体会数学知识的重要性.
(3)教学目标.知识目标:理解对数的概念,懂得指数和对数的互化.能力目标:培养逻辑推理能力和数学运算能力.情感、态度和价值观:从历史发展过程中去了解对数产生的意义,引发学习的渴望,自然而然地引出对数的概念.
(4)教学重难点.重点是对数的起源和对数的概念.难点是对数与指数的互化.
2.2 教学过程
教师:今天我们学习对数的概念.对数的产生最早是为了解决计算的问题.大家看一个例子.
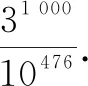
学生:计算器也很难算出来!
教师:为了解决这个问题,数学家们引进了一个符号:“lg”,读作:以10为底的对数.运用它的一些运算法则,除法运算可以变为减法运算,指数可以“下来”变系数.
(板书.给出参考数据:lg 3=0.477,1g 10=1.)
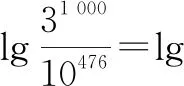

设计意图:采用顺应式改编了历史材料1——布拉赫的困扰,让学生初步了解对数对于计算的重要意义,认识到对数在“简化运算”中的作用;引发学生学习的强烈愿望,为第二课时“对数的运算”做好铺垫.
例2纳皮尔精确的对数定义来源于一个运动的几何模型.为了便于同学们更好理解,我们简化了他的模型.假设有两个沿两条直线运动的质点.点P从起点A开始在线段AB上运动,同时点Q从起点C开始沿射线CD运动.设点P与终点B的距离PB=x(t),点Q与起点C的距离CQ=y(t).测量后知道:x(t)=2t,y(t)=3t.
(1)当点P运动了一段时间,PB=2时,点Q的位置?
(2)当点P运动了一段时间,PB=3时,点Q的位置?
学生:(1)当x=2时,t=1,则y=3.
教师:会解吗?
学生摇头.
教师:为了解决这个问题,我们引进对数的概念.把t称为是以2为底3的对数.
设计意图:采用顺应式改编了历史材料2——纳皮尔的对数,避免了繁杂的分析,问题通俗易懂,直接引出对数的概念的重要性,顺理成章地进行对数概念的讲解,也为以后学习对数函数的概念埋下伏笔.
教师:一般地,如果ax=N(a>0,且a≠1),那么把指数x叫做以a为底N的对数,记作x=logaN,a叫做对数的底数,N叫做真数.(强调了x是指数.)
当a>0,且a≠1时,ax=N⟺x=logaN.
教师:对于例3的第(2)问,大家试试,现在能解决吗?
学生:t=log23,则y=3log23.
教师:总结一下,对数是什么?
学生:①logaN是一个数;②这个数记为x,则x=logaN满足ax=N(x在指数位置).
设计意图:课堂小结非常重要,它是学生学了一节课后对知识的梳理.根据教学经验可以知道,学生第一次接触对数是很难理解的.总结对数的本质是非常有必要的.
上文只是对数概念引入的教学设计,接下来的教学内容就是用课本的题目巩固和练习,在此就不详细说明.
HPM的引入使学生对对数概念的理解更加深刻,对对数意义的领悟更加透彻.一开始问题的提出,造成学生心理的疑问,在适当的时候及时解决,学生有一种茅塞顿开的感觉.
