立足“三新”背景,强化“四基”应用,培养核心素养*
——“复数”大单元复习设计与安排
2023-08-04江苏省灌云高级中学
江苏省灌云高级中学 孙 红
在新教材(人民教育出版社2019年国家教材委员会专家委员会审核通过)、新课程(《普通高中数学课程标准(2017年版2020年修订》)、新高考“三新”背景下,“复数”大单元的复习教学设计更加侧重于“四基”层面,合理创设知识网络与体系,注重复数概念的基础性,凸显复数运算公式的应用性,拓展数学思维的灵活性,联系复杂创新场景与数学文化等,有效进行大单元复习教学设计与安排[1].
1 构建知识网络,厘清单元系统
涉及“复数”大单元知识模块,关键在于构建复数的概念、运算与应用等的知识网络,“串联”起各个知识点之间的联系,形成各个节点,全面厘清单元系统,为知识的进一步理解与深化,以及综合应用等创设条件[2].
以上“复数”单元的知识网络(如图1)中,从数学基础知识、基本技能、基本思想、基本活动经验这“四基”的不同视角来展开,并加以联系,关注学生对“四基”的落实情况,以及发现问题、提出问题、分析问题与解决问题能力的培养与提升情况,重视数学核心素养的养成与发展.
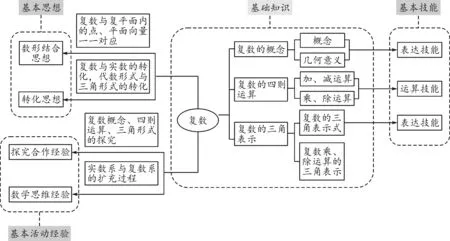
图1
2 重视概念学习,辨析区别联系
“复数”大单元中涉及较多的概念,正确学习并理解对应的概念,以及不同概念之间的区别与联系,特别是相互之间的差异,为解决问题提供条件.
这里主要涉及复数、实数、虚数、纯虚数、共轭复数、复数相等等相关概念,关键在于厘清对应的概念与实质,并能合理辨析它们之间的区别与联系.
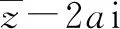
A.第一象限 B.第二象限
C.第三象限 D.第四象限
分析:从创新定义入手,结合复数的四则运算,确定参数的值,并结合共轭复数的概念以及复数的几何意义等来转化与应用.
解析:由z=(2+ai)i=-a+2i,结合创新定义“等部复数”,可知-a=2,解得a=-2,即z=2+2i.
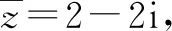
故选择答案:A.
点评:这里通过创新定义,巧妙把众多的复数概念融合其中,包括复数的实部与虚部、共轭复数、复数的几何意义等,结合复数的四则运算加以综合,合理辨析概念,巧妙求解.
“复数”大单元中除了本单元内的基本概念外,经常会通过数学文化场景、创新定义创设等方式引入一些新的概念.解题时要与已知概念进行对比与分析,进而加以正确理解与巧妙应用,实现知识与思维的全面发展.
3 强化复数“公式”,增强数学运算
“复数”大单元中,正确理解并掌握复数的四则运算的,可为进一步的复数运算与应用奠定基础.这里主要涉及复数的加法、减法运算及其几何意义,以及复数的乘法与除法运算等,还有复数范围内的实系数一元二次方程问题等[3].
例2若实系数一元二次方程x2-2x+3=0的两个根为α和β,则|α|+|β|=________.
分析:根据题目条件,利用实系数一元二次方程的求根公式直接求解两个根α和β,再利用复数的模的求解来分析与处理;也可以利用实系数一元二次方程虚根成对(互为共轭复数)的性质确定两虚根的和与积,引入参数并结合复数模的公式来分析与求解.
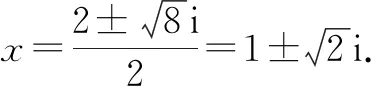
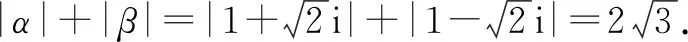
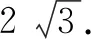
解法2:(性质转化法)由判别式Δ=b2-4ac=(-2)2-4×1×3=-8<0,知实系数一元二次方程虚根成对,且互为共轭复数.
设α=a+bi,a,b∈R,则β=a-bi.
由韦达定理,可知α+β=2a=2,αβ=a2+b2=3.
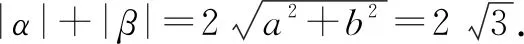
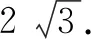
点评:实际解决复数范围内的实系数一元二次方程问题时,可借助复数的四则运算加以剖析与应用,也可以直接利用相关的性质加以转化与应用.这也是新教材中的一个明确要求.
“复数”大单元中,复数范围内的实系数一元二次方程问题,在新教材中直接作为例题来设置,通过例题的解析,归纳总结出复数范围内实系数一元二次方程的求根公式,并给出明确要求,这与原来旧教材中作为课外补充知识形成鲜明的对比.
4 开拓数学场景,关注数学文化
“复数”大单元中,由于复数自身的知识结构特点以及数学文化背景,此部分的试题经常与数学文化加以巧妙融合,以创新情境来合理设置,成为高考命题中的一道具有基本特色的风景线.
例3欧拉公式eiθ=cosθ+i sinθ把自然对数的底数e、虚数单位i、三角函数cosθ和sinθ联系在一起,充分体现了数学的和谐美,被誉为“数学中的天桥”,若复数z满足(e2 023iπ+i)·z=i,则z的虚部是________,|z|=________.
分析:根据题设中的欧拉公式计算出e2 023iπ的值,结合关系式的变形,以及复数的除法运算得到复数z,再利用复数的相关概念求得z的虚部与复数的模|z|.
解析:由eiθ=cosθ+i sinθ,可得
e2 023iπ=cos 2 023π+i sin 2 023π=-1.
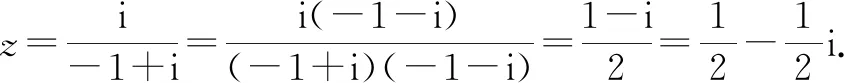
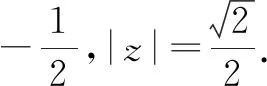
故填答案:
点评:以数学文化中的创新情境给出欧拉公式,结合复数三角形式与指数形式来创设问题,结合关系式的变形与转化,利用复数代数形式的四则运算来进行运算求解,并结合相关的概念来实现问题的融合与创新.
5 优化数学思维,关注推理应用
“复数”大单元中涉及较多的数学思维,如函数与方程思想、数形结合思想、类比思想等,都是解决复数问题中比较常用的数学思维.全面拓展并应用数学思维,可以使得数学知识的学习更加牢固,数学问题的解决更加简捷.
例4化简:(cosθ+i sinθ)2,(cosθ+i sinθ)3,(cosθ+i sinθ)4,由此猜想一般的结论:(cosθ+i sinθ)n=________(n∈Z).
分析:例4其实就是复数三角形式的乘方运算,是高中数学教材中的选讲内容之一,具体解决问题时,可以利用复数的四则运算与三角函数关系式加以化简,通过归纳总结,猜想而得出结果.
解析:由(cosθ+i sinθ)2=(cosθ+i sinθ)(cosθ+i sinθ)=cos 2θ+i sin 2θ,
(cosθ+i sinθ)3=(cos 2θ+i sin 2θ)(cosθ+i sinθ)=cos 3θ+i sin 3θ,
(cosθ+i sinθ)4=(cos 3θ+i sin 3θ)(cosθ+i sinθ)=cos 4θ+i sin 4θ,
归纳猜想,可得(cosθ+i sinθ)n=cosnθ+i sinnθ.
故填答案:cosnθ+sinnθ.
点评:根据题设条件先确定前面若干问题,进而找到规律,归纳、猜想出一般性的结论.同时,这也给我们提供了一种解题思路——当“无路可走”时,可考虑多探究前面若干问题,归纳出规律并大胆猜想后再给出证明.这种解法虽操作简单,但需较强的观察、分析和归纳等关键能力.
在“三新”(新教材、新课程、新高考)背景下,进一步落实“双减”政策与新改革理念,积极贯彻《总体方案》要求.“复数”大单元复习教学设计与安排,在寻求基础、本质、能力、创新等的基础上,更多侧重数学基础与关键能力的考查,坚持开放创新与核心素养导向,更加注重数学创新意识与创新应用[4].
