变粒径喷雾除尘系统喷雾压力控制方法

杨凯凯,甘树坤,吕雪飞

(吉林化工学院 机电工程学院,吉林 吉林 132022)

随着工业化进程的不断发展,工业生产导致空气中产生过量的粉尘,严重恶化了人们的工作和生活环境,同时也会缩短设备的使用寿命,给生产带来安全隐患[1]。目前变粒径喷雾除尘系统的喷雾压力控制普遍采用常规的PID控制方法,但是传统的PID控制适用于可建立精确数学模型的线性系统,然而实际的变粒径喷雾除尘系统的喷雾压力控制往往是非线性的、时变不确定性的,因此很难建立精确的数学模型,使得传统PID控制的变粒径喷雾除尘系统的喷雾压力控制的参数整定麻烦、性能欠佳、对运行工作情况的适应性很差[2-3]。针对上述问题,本文提出了一种基于BP神经网络PID变粒径喷雾除尘的喷雾压力的控制方法,对喷雾压力这个影响喷雾粒径大小的参数进行优化设计,以探求其合理的控制方法,提高变粒径除尘系统的除尘效率。

1 除尘机理

粉尘是指粒径在75 μm的固体悬浮物。喷雾除尘是通过喷射的雾滴颗粒与空气中的粉尘颗粒接触,并与其结合,增大粉尘颗粒的质量,使其在重力作用下迅速沉降,实现除尘效果。雾滴和空气中的粉尘通过碰撞效应、拦截作用、布朗扩散作用以及粉尘自身受到的重力作用来实现除尘目的[4]。

在喷雾除尘的过程中,最容易除去的是粒径大的粉尘,因此粉尘粒径越大,除尘效率越高。根据文献[5]研究粉尘粒径和喷雾粒径的关系,即：

(1)

式中：dfmin为喷雾捕集粉尘最小粒径;μ为空气动力黏度;D为雾滴粒径;Stk为惯性碰撞系数;ρf为粉尘密度;V0为气流速度。

由式(1)可知,喷雾捕集粉尘的最小粒径和雾滴粒径成正比关系。根据文献[6]研究雾滴粒径和喷雾压力的关系,即：

(2)

式中：k为实验室系数;d为喷雾出口直径;p为喷雾压力。

由式(2)可知,在外部条件因素不发生变化时,喷射的雾滴粒径大小和喷雾压力成反比关系,即喷雾压力越大,喷雾粒径越小。本文是基于气液两相流的喷头研究的,因此喷雾压力p是空气和水压力的和,改变空气压力大小可以使喷出的喷雾粒径大小发生改变。文献[7]～[9]研究发现雾滴粒径和粉尘之间存在耦合关系,即当雾滴粒径与粉尘粒径接近时,粉尘被除去的概率变大。

因此,在喷雾除尘的过程中,通过改变空气压力的大小来调整喷雾装置喷射雾滴的粒径大小可以提高除尘效率。

2 喷雾除尘系统组成与控制方法

2.1 喷雾除尘系统组成

设计的改进BP神经网络PID喷雾除尘系统主要由电源、粉尘浓度传感器、空压泵、储气罐、空气比例阀、抽水泵、蓄水箱、电磁阀、压力表、西门子S7-1200 PLC、触摸屏、激光粒径仪组成,如图1所示。

图1 喷雾除尘系统硬件结构图

工作时空气从储气罐出来通过气比阀控制进入喷头;水从蓄水箱出来通过抽水泵经过水流量计和水压表、止回阀进入喷头,PLC连接空比阀、气压计,负责接收和发送系统运行参数。

2.2 喷雾除尘系统控制策略

本研究设计的变粒径喷雾除尘系统的技术目标是系统产生的实际喷雾压力可根据设定值进行精准、稳定且快速的调节,喷雾除尘系统结构框图如图2所示。

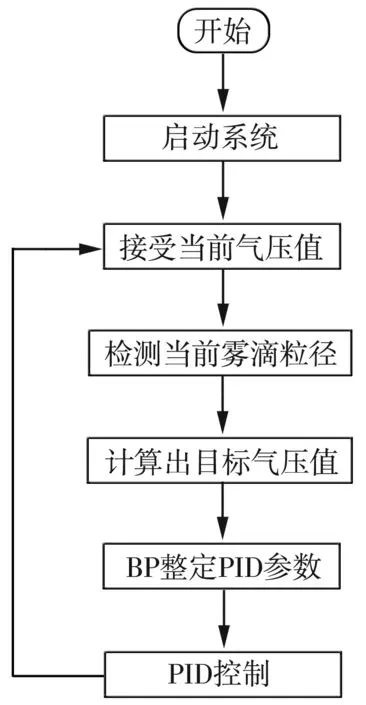
图2 喷雾除尘系统控制结构图

喷雾系统作业时,触摸屏上位机设置喷雾系统定值,PLC接受设定后迅速响应,调整至目标气压,并根据压力传感器检测的实际压力与目标压力之间的差值进行BP神经网络PID运算,最终输出相应的输出信号,控制空气比例阀调整阀门开度,使得实际的喷雾压力跟随设定值的变化进行快速自动调节。

2.3 BP神经网络算法

BP神经网络的优点在于能够通过网络连接权值的多次代入计算来修正误差,不断接近适应度函数[10]。使用BP神经网络算法搭建PID控制,利用BP神经网络算法可以不断接近适应度函数的能力,快速寻找到最优的PID参数,提高控制系统的动态性能。

如图3所示,本文搭建的BP神经网络是一个三层网络结构,输入层的三个输入分别是e(k),e(k-1),e(k-2),输出层的三个输出分别是Kp、Ki、Kd,BP神经网络的输入层节点的输入为

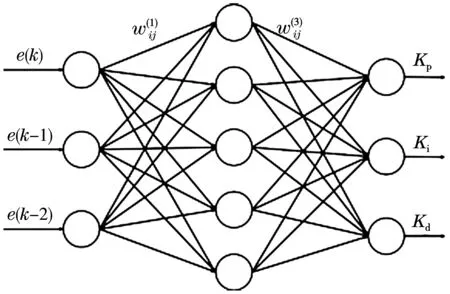
图3 BP神经网络的结构模型

(3)

BP神经网络的隐含层输入输出为

(4)

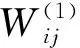
BP神经网络的输出层输入输出为

(5)

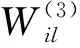
性能指标函数为

(6)

式中,r(k+1)为期望输出空气压力值;y(k+1)为压力传感器实际检测的空气压力值;

为了改进BP神经网络收敛速度慢的问题,本文的BP神经网络算法以误差的平方作为目标函数,具有很好的预测效果。即,隐含层的输入为

(7)

通过使用梯度下降法从负梯度方向对BP神经网络的权值系数实施参数调整,计算目标函数的最小值,输出层连接权值系数可表示为

(8)

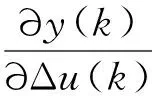
由式(1)和式(5),可求得：

(9)

若误差e(k+1)满足,e(k+1)>e(k),那么其学习速率按照φ=0.5φ减小,反之则记录权值系数。

2.4 增量式PID

增量式PID控制响应速度快、超调量较小、稳定性较好[11],更适合喷雾除尘系统实时性的需求,因此本研究采用增量式PID控制喷雾除尘系统的压力调节算法：

Δu(k)=Kp[e(k)-e(k-1)]+Kie(k)+Kd[e(k)-2e(k-1)+e(k-2)].

(10)

u(k)=Δu(k)+u(k).

(11)

式中：Kp为比例系数;Ki为积分系数;Kd为微分系数;k为采样序号,(k=0,1,2,3…);e(k)为第k次采样压力偏差量;u(k)为第k次采样实际压力值。

结合改进的BP神经网络算法后,如图4所示。

图4 BP神经网络PID控制器

系统BP神经网络PID控制器的输入是实际喷雾压力和期望值之间的偏差,再通过调整BP神经网络的连接权值和学习速率,对PID控制器的Kp、Ki、Kd进行自动调参,逐步使实际喷雾压力逼近目标压力。然后通过喷雾粒径仪实时检测的喷雾雾滴粒径和粉尘粒径的大小根据式(1)的函数关系进行分析对比,改变输入空气压力目标值的大小,实现喷雾系统的变粒径喷雾功能,提高除尘效率。

2.5 算法实现过程

(1)确定BP神经网络结构,在实际控制过程中,可以通过调整隐含层节点个数的多少使得BP神经网络有更有效的控制效果[12]。同时对BP神经网络的权值Wil、学习速率φ和惯性系数α进行初始化。本文的BP神经网络是一个三层结构,其输入层节点数n(1)=3,隐含层节点个数n(2)=5,输出层节点个数n(3)=3。在其他参数调整好的情况下,隐含层节点数为5时,控制效果最好[13]。

(2)实时采样,计算期望输出空气压力值r(k+1)与压力传感器实际检测的空气压力值y(k+1)的差值e(k);然后根据增量式PID控制器进行计算,得到u(k)送至BP神经网络进行实时控制。

(3)根据式(3)～(9),对BP神经网络进行编程获取各个神经元节点的输入和输出;观察控制效果,然后通过经验调整权值参数。

(4)返回到步骤(2)进行循环控制。

3 仿真实验

为了验证所提出的基于改进BP神经网络PID的变粒径喷雾除尘系统喷雾压力控制方法的控制效果,本文基于Simulink搭建了仿真模型,针对喷雾除尘系统空气压力控制响应时间、超调量和稳定性状况,分别使用传统PID控制器和改进的BP神经网络PID控制器设计并进行了对比仿真实验。

如图5所示,初始化和仿真循环组成了Simulink仿真设计[14]。其中BP神经网络PID控制器的调整参数功能主要通过S函数程序结构实现,即图4“bp”模块,通过把不同的标志位和子函数集合,进行求解器和系统之间的信息传递,达到控制效果。

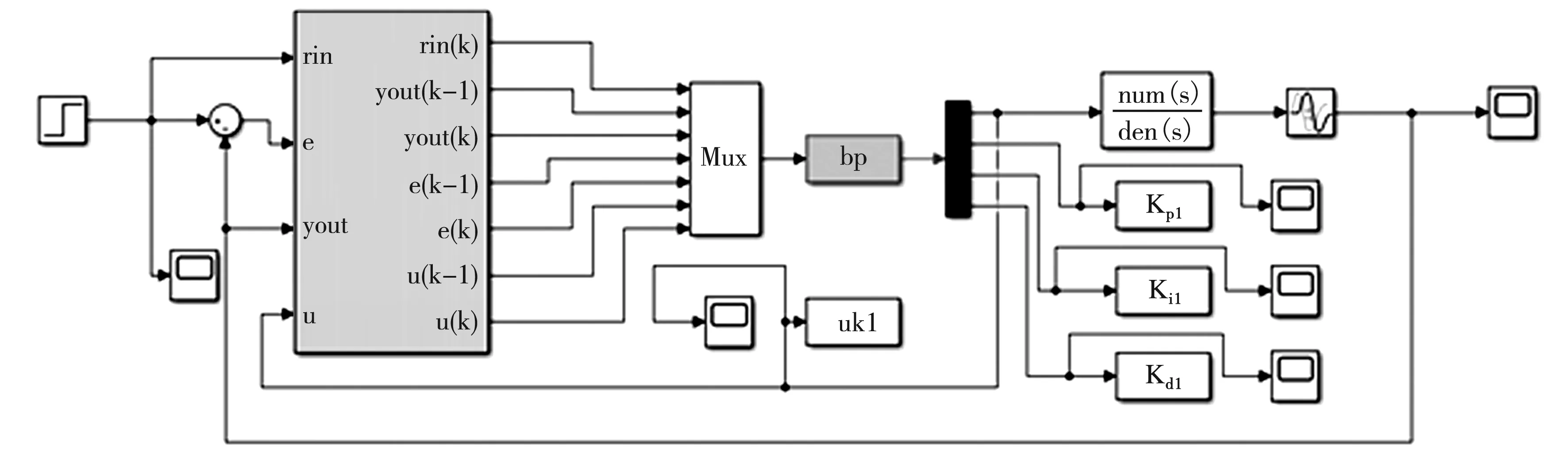
图5 基于BP神经网络PID控制器的Simulink仿真模型

传统的PID控制参数选取经验调整参数后的固定数值：Kp=20、Ki=10、Kd=0.1;仿真所用部分参数见表1。

表1 仿真验证部分参数

图6(a)～(b)表示改进的BP神经网络PID控制器分别对阶跃信号和阶梯信号的响应情况。由图6(a)可以得出改进的BP神经网络PID对喷雾除尘系统的压力控制,其响应时间为3.44 s、超调量为1%;由图6(b)可见：改进的BP-PID控制器有很好的跟随效果;图6(c)为传统PID控制器和改进的BP-PID控制器对阶跃信号的响应曲线的对比图,仿真结果的具体参数如表2所示,使用了BP神经网络优化的PID控制器与传统PID控制器相比较,响应速度提高了66.63%,稳定性提高了20%。由此可见,改进的BP-PID控制器相对于传统的PID控制有更快的响应速度和更小的超调量;图6(d)表示BP神经网络对PID控制器Kp、Ki、Kd这三个参数的自动调参的情况。在控制的开始阶段,BP-PID控制器的比例系数减小,从而系统的快速性较之前有所减慢;但积分系数的增大,最终使得BP-PID控制器的响应速度在开始阶段与传统PID控制器的快速性相差不大;而在系统即将达到稳态时,积分系数减小,比例系数增大,从而可以大大减小系统的超调量,同时可以使系统在稳态时的响应速度更快、精度更高。

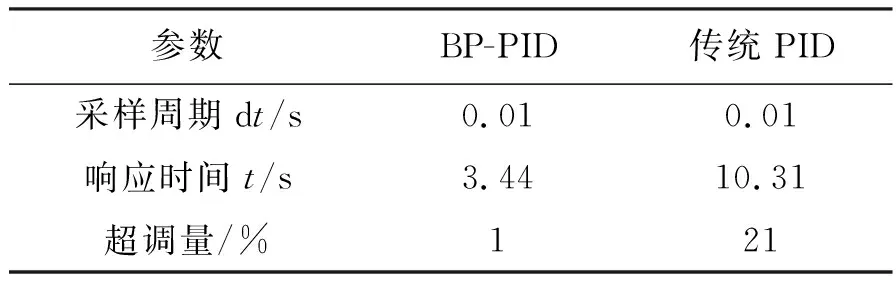
表2 Simulink对比实验结果

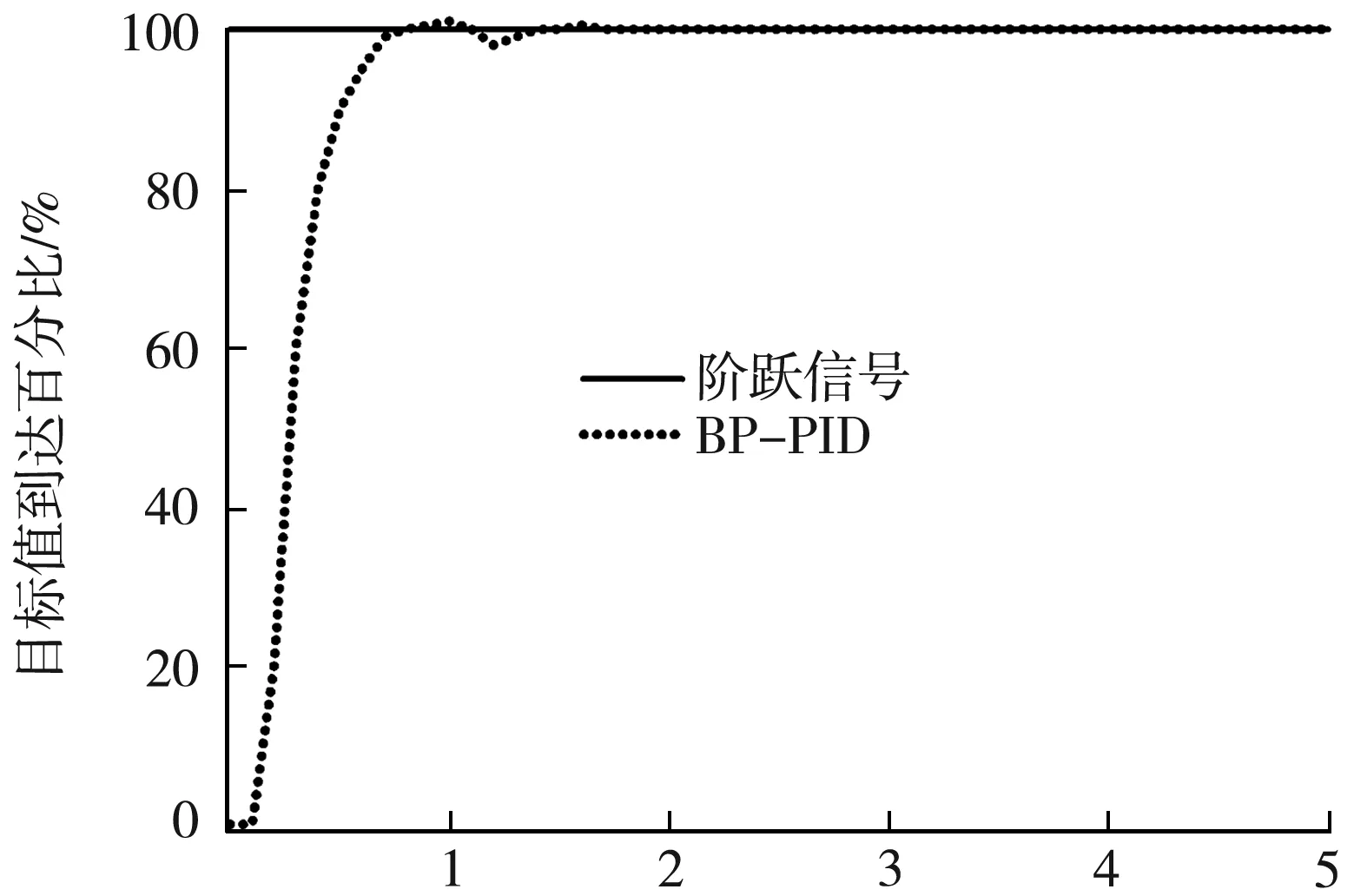
(a) 阶跃信号图

由此可知,BP神经网络PID控制器收敛速度更快、精度更高,可以很好地应用于控制系统中,同时也验证了变粒径喷雾除尘系统对喷雾压力控制的可靠性与正确性。

4 结 论

变粒径喷雾的喷雾除尘系统在工业、环境治理等领域的应用非常广泛,但实际应用中存在喷雾压力控制具有干扰量多、大滞后、非线性等缺点。为解决此问题,提高系统的控制精度和除尘效率,本文将BP神经网络算法应用到增量式PID上,利用BP神经网络可以快速逼近适应度函数的能力,实现了对增量式PID参数的自适应调整,将该算法用于变粒径喷雾除尘系统的喷雾压力控制中。通过仿真实验,结果表明本研究的控制方法能够提高变粒径喷雾除尘系统对喷雾压力控制的速度和精度,达到了有效除尘的控制效果,同时也验证了该方法的可行性和有效性。