基于混合核搜索优化与麻雀算法的经济排放调度问题研究

董如意,马 龙

(吉林化工学院 信息与控制工程学院,吉林 吉林 132022)

在电力市场中,通过分配发电机组功率减少燃料消耗,使发电成本减到最低,以获得竞争优势,是电力系统经济调度(ELD)领域一直以来的研究问题。同时,ELD需要满足电力系统的负荷需求和网络损耗。随着人们对环保的日益关注,减少火电厂生产过程中产生的污染排放,成为了关键问题。然而,ELD和减排是两个冲突的目标,在选择最小的发电成本时,必然增加污染排放。因此,同时考虑最小化燃料消耗和污染排放的联合经济排放调度(CEED)问题已经成为一个研究热点。传统数学优化算法在求解CEED问题的过程中,随着问题复杂度提升和维度增加,会出现非可行解,并且对初始解比较敏感,容易陷入局部最优。因此,很多文献提出元启发式算法来求解EED问题。文献[1]使用模糊计算方法,通过改进的细菌觅食算法(MBFA)来求解EED问题。通过两个CEED案例测试,结果表明,MBFA算法具有较好的鲁棒性和可靠性。文献[2]采用改进的散点搜索(ISS)来解决EED问题。通过IEEE 30标准总线6发电系统测试,实验表明,ISS算法是一种行之有效的解决CEED问题的方法。文献[3]提出Pareto蜂群优化算法,并将其应用于IEEE 30标准总线系统,解决EED问题。实验结果优于其他多目标优化算法。文献[4]提出了一种改进版本的黏液霉菌算法(ISMA),并用于解决EED问题。在5个案例上对算法进行了验证,结果表明,ISMA算法相比其他算法具有更好的收敛性和鲁棒性。文献[5]提出了核搜索优化算法(KSO),通过将非线性的目标函数投射到高维空间将目标函数转化为线性函数,并应用于3个带阀点的案例,实验表明,相比于其他算法KSO算法具有更好的性能。

本文提出了一种新的改进优化算法(HKSOSSA),通过结合麻雀算法(SSA)的预警机制,增强原始KSO算法的局部寻优能力[6]。并对预警机制进行改进,使得最终结果易于收敛。并将其应用于EED问题,通过国际通用的IEEE 6机30节点标准系统进行计算验证。

1 数学模型

1.1 目标函数

燃料成本的函数形式可以表示为[7]

(1)

其中,C为消耗燃料的成本;ai、bi、ci为第i个发电机的成本系数;ei、fi为阀点效应系数;Pi表示第i个发电机的有功出力;N表示发电机组数。

有害污染排放的函数形式可以表示为[8]

(2)

其中E为有害污染的排放量;ai、βi、γi、ηi和δi为第i个发电机组的排放系数。

这是一个具有两个不同目标的多目标优化问题。为了解决这一问题,采用加权和的方法引入权重因子,将C和E合并为单个目标的函数形式。合并后的函数形式为[9]

F=wC+γ(1-w)E,

(3)

其中w为权重因子;γ为比例因子。

1.2 约束条件

(1) 功率平衡约束：所有发电机的总功率必须包括负荷需求和实际电力系统损失的总和[10]。

(4)

其中,N为发电机系数;Bij为网损系数;PL为有功网损;PD为有功负荷。

(2) 功率容量限制：每个发电机的相对输出范围(最大-最小)。

(5)

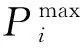
元启发式算法不能处理有约束条件的优化问题,不等式约束式(4)通常难以满足,因此,采用牛顿法迭代来满足方程的约束。

2,…,N-1 ,

(6)

其中,Pi为第i个发电单元的输出。

对于第n个发生器的原始输出,可以迭代求解式(4)。

(7)

(8)

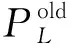
(9)

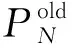
(10)

其中,λ是一个惩罚因子。

2 改进KSO算法

2.1 KSO算法概述

文献[5]提出了一种基于核方法搜索策略的群智能算法。KSO与传统的生物或物理搜索策略不同,它是基于纯数学的搜索策略。与已有的物理或生物搜索策略(physical or biological,MAs)有明显的区别。

已有MAs都是通过非线性迭代来接近目标函数的最优值,而KSO是通过核函数法进行线性迭代。利用核映射函数将非线性的目标函数转化为高维空间中的线性目标函数。随着空间维数的增加,非线性函数转化为线性函数的可能性越来越大。即：

y=f(x)=wT·u+b,

(11)

其中m为高维空间的维数;w=(w1,w2,…wm,u(u1,u2,…um)均为m维向量。

由n维向w量映射为a=(a1,a2,…,an)的m维向量,即w=φ(a)。m维超平面的斜率为最优值所在的方向,用φ(a)表示,则：

y=f(x)=wT·u+b=φ(a)·φ(x)+b=

K(a,x)+b,

(12)

其中K(a,x)为核函数,作为一个高维空间中的函数,其最优值是低维目标函数的解。

选择RBF函数作为核函数,RBF函数可以将目标函数映射到无限高维空间[12](KSO),使非线性函数转化为线性函数。

(13)

式(13)通过目标函数的一次迭代,给出了最优问题的近似解。拟合核函数的最优结果可近似视为目标函数的最小值,经过多次迭代,使其接近于可能的最优结果。

最小值与向量a等价,对应着映射到高维超平面斜率的低维原像。a称为核向量,它指向一个特定方向的迭代优化过程搜索。具体用式(14)求解。

σln(y-b)=‖x-a‖2=(x1-a1)2+(x2-a2)2+…(xn-an)2,

(14)

(15)

(16)

得到a和σ后,对x进行如下更新：

(17)

其中,t和Tmax依次为当前迭代次数和最大迭代次数。

2.2 麻雀优化算法概述

麻雀搜索算法的灵感,来源于生物界麻雀捕食和反捕食行为[6]。当种群中的发现者率先发现食物,其余的跟随者会跟随发现者向食物源靠近。同时,会选取SD只麻雀负责警戒,当天敌接近时,会发出预警,带领种群前往其他位置。

其中,警戒麻雀的位置更新公式为

(18)

其中,Xbest表示全局最佳的位置;β和k为步长调整系数;f为麻雀的适应度值;fg和fw依次为全局最优和最差适应度值;ε是一个极小常数。当fi>fg时,表明麻雀处于种群不安全的边缘地带,容易被天敌发现,需要向种群中心的麻雀靠拢;fi=fg时,表明在种群中心的麻雀容易被天敌袭击,必须尽快向种群中其他麻雀靠拢。

2.3 改进HKSOSSA算法

提出的HKSOSSA算法通过混合麻雀算法的预警机制,增强原KSO算法的局部寻优能力。同时改进了原始麻雀算法的预警机制,平衡全局搜索和局部搜索的比重,使得最终结果更易于收敛。

式(19)为改进的预警机制：

(19)

其中,SD为挑选负责的警戒麻雀数量;w1和w2表示初始和最终警戒麻雀的数量。

改进算法的流程见图1。

图1 改进HKSOSSA算法流程图

3 结果与讨论

将HKSOSSA优化算法应用于电力系统经济排放调度优化问题中,选择有功负荷为283.4 MW,国际通用IEEE 6机30节点标准系统作为算例,并考虑罚点效应[11]。实验在Matlab2020b软件上实现,并在Intel Core CPU i7-10700@4.59GHz(8 CPU),32GB RAM运行环境下执行,操作系统为Windows10专业版。HKSOSSA算法参数设置如下：种群数量N=30;最大迭代次数Tmax=1 000;警戒粒子数量SD参数,w1=0.3,w2=0.2。

表1给出了罚点效应权重w从0到1,步长为0.1情况下求解的最优结果,同时考虑了发电约束和电网传输损耗。如表2所示,当把发电成本最小化作为目标函数时,HKSOSSA算法得到的最小发电成本为605.879 0($/h)。当只考虑减少排放时,HKSOSSA算法达到的最小排放量为0.194 178(ton/h)。

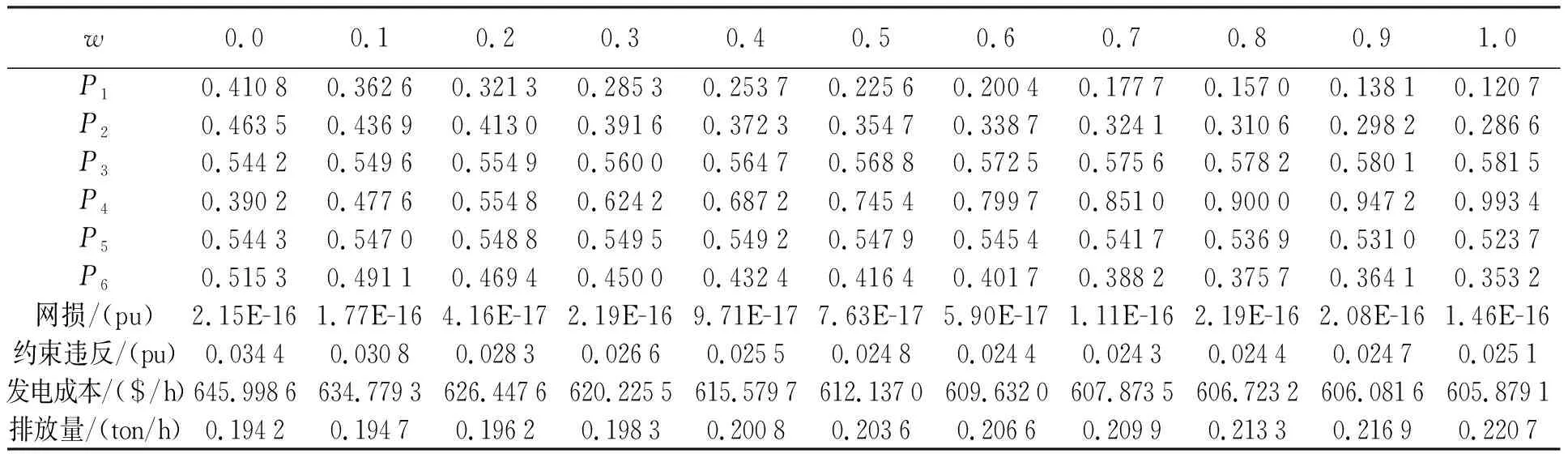
表1 不同罚点效应权重对应的发电成本和排放量

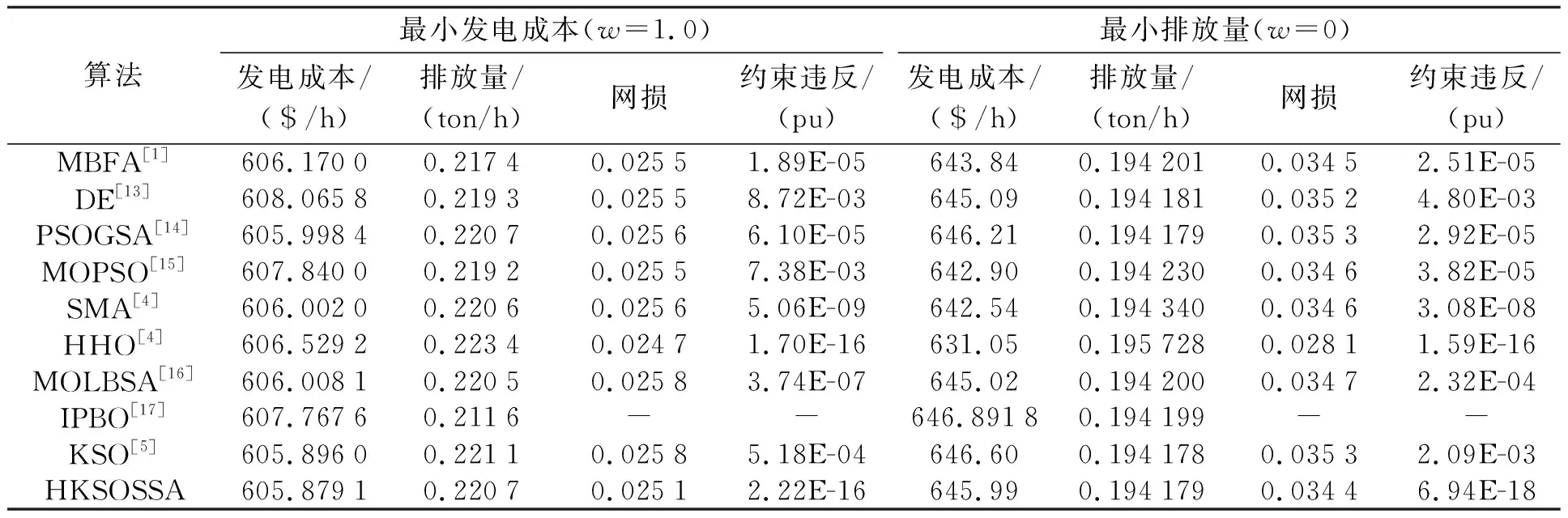
表2 不同算法最小化发电成本和排放量的比较结果

表2记录了各种优化算法得到的最小化发电成本和最小化排放量。考虑最小发电成本时,HKSOSSA算法在所有算法中获得了最优的结果,相比原始KSO算法降低了0.016 9($/h)的燃料成本。当考虑最小排放量时,HKSOSSA、KSO和PSOGSA结果接近,优于其他算法,而且HKSOSSA得到结果电网传输损耗最小。

4 结 论

本文提出了一种新的改进优化算法(HKSOSSA),增强原KSO算法的局部寻优能力,使得最终结果更容易跳出局部最优且易于收敛。并将其应用于电力系统的经济排放调度问题,在考虑电网传输损耗和发电约束的情况下,用国际通用的IEEE 6机30节点标准系统对本文算法进行验证,并与原始KSO算法及其他优化算法进行比较。实验结果表明,本文提出的算法能够获得比传统KSO算法更好的结果,是一种解决电力系统经济排放调度问题的有效方法。