基于遗传算法的集中供热系统PID参数整定
2023-08-04高思航孟亚男姬庆宽张心人境
高思航,孟亚男,姬庆宽,张心人境
(1.吉林化工学院 信息与控制工程学院,吉林 吉林 132022;2.长垣盾安节能热力有限公司,河南 长垣 453400)
近些年来我国集中供热事业得到了飞快发展,城镇供暖覆盖面积逐年递增,供热管网的重要性也日渐突出,其中换热站温度控制的优劣决定着供热质量和能源消耗。为此,对换热站温度控制系统的优化研究刻不容缓[1]。
文献[2]提出了采用专家系统整定PID参数的方法,该方法虽然具有可靠性高,可以在线控制PID等特点,但是专家控制需要很多的专业知识与经验,花费巨大的人力,不适宜推广应用。文献[3]提出一种模糊PID参数自整定控制方案,能够提高系统的稳定性,但不具有普适性。文献[4]利用了BP神经网络的PID函数,但BP神经网络很容易陷入局部最小值。
根据这一现状,本文提出采用遗传算法与PID相结合的算法,设计出GA-PID控制器。并将仿真结果与BP-PID和传统PID相对比,结果表明该系统具有响应速度快、调节时间短等优点。系统的控制效果有了显著的提高。
1 总体控制方案的设计
由于集中供热系统的非线性、时变性等因素导致控制效果并不理想,同时PID参数一旦被确定无法自动修改,缺少自适应调参功能,且现场人员临时调参危险系数较高[5]。如果仅采用PID控制,则很难满足控制需求。因此,将PID控制与其他优化算法相结合是一种必然的趋势。
1.1 PID控制器
传统PID控制系统仍是换热站中温度控制器最常用的控制方法,该方案具备了控制精度高等优势[6]。其控制系统原理图,如图1所示。
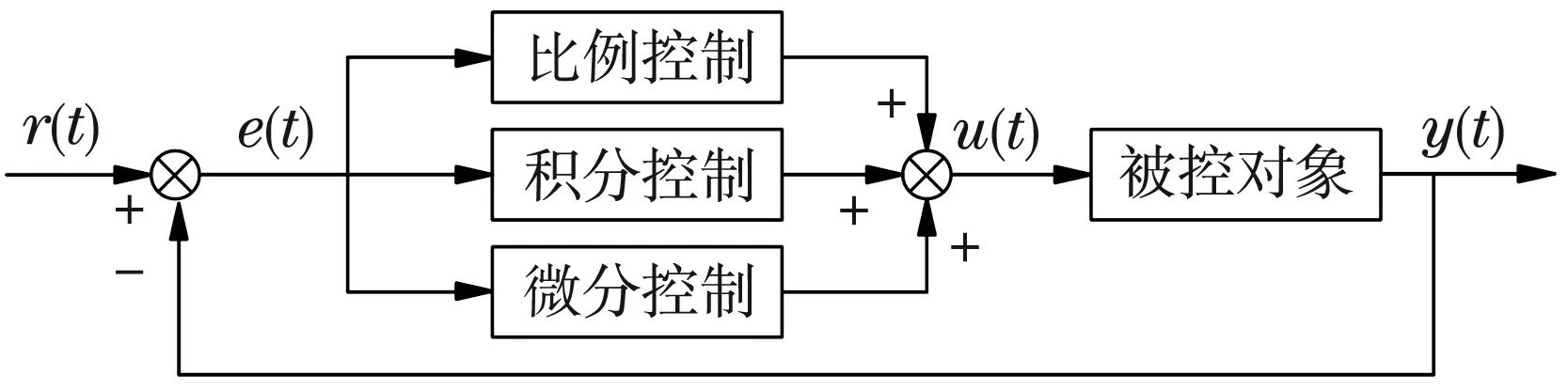
图1 PID控制系统结构图
PID控制器根据给定值和输出值构成控制偏差:
e(t)=r(t)-y(t).
(1)
它的控制规律为
(2)
式中:Kp为比例因子;Ti为积分时间;Td为微分时间。
经典增量式数字PID的控制算法为
u(k)=u(k-1)+Kp[e(k)-e(k-1)]+Kie(k)+Kd[e(k)-2e(k-1)+e(k-2)].
(3)
1.2 BP神经网络控制器
Back Propagation网络的控制器由两部分组成,分别是传统PID控制器和神经网络控制器[7]。经典的PID控制器,结构简单,可以在线调整比例积分微分的参数。神经网络控制器的输出分别对应Kp、Ki、Kd参数,通过系统运行,循环往复误差反馈调整权值系数得出最优的参数值[8-9]。BP-PID控制结构图如图2所示。
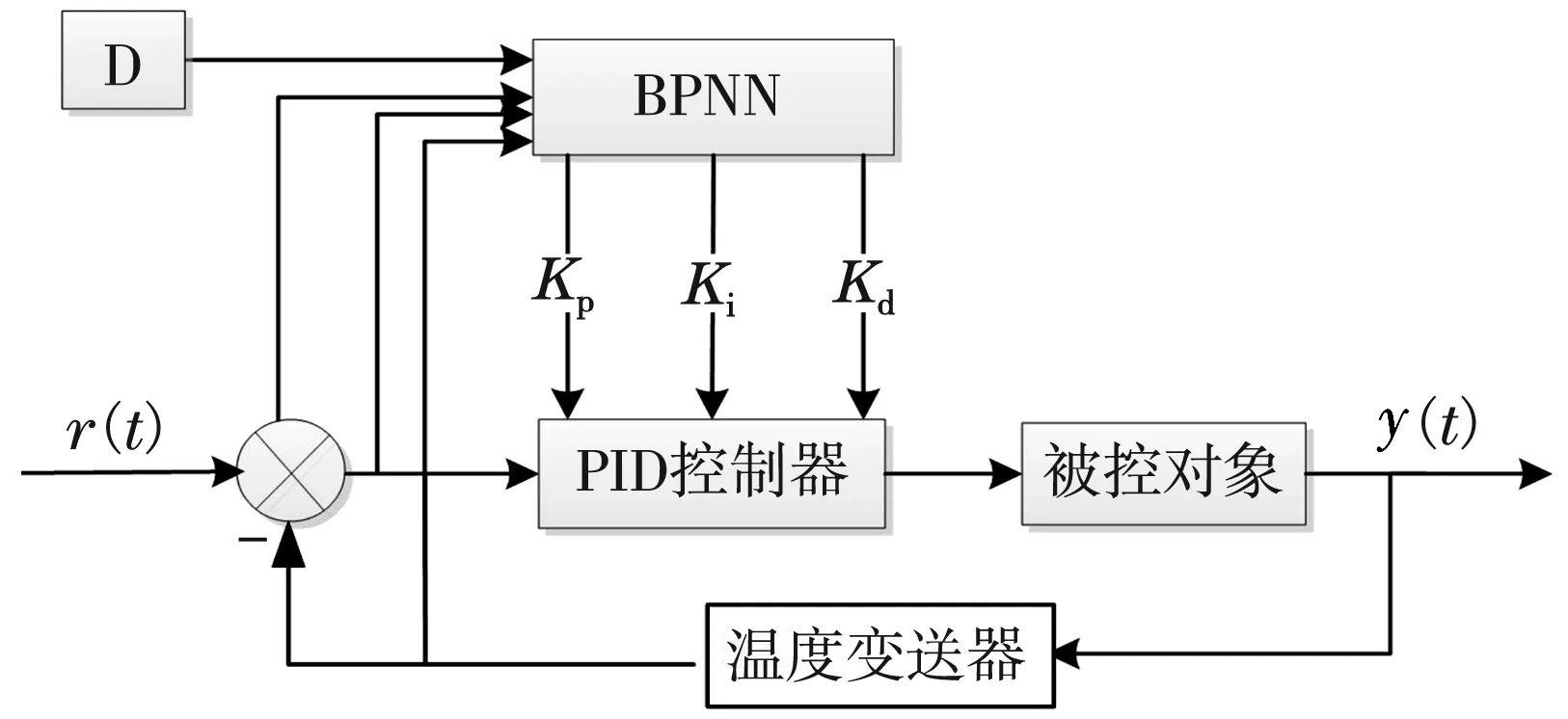
图2 BP-PID控制系统图
神经网络输入层的输入为
Qi(k)=x(i) ,i=1,2,3…M.
(4)
式中,M的个数取决于系统的复杂度。
隐含层的输入与输出:
(5)
(6)
输出层的输出与输入:
(7)
由此可求出Kp、Ki、Kd,即
(8)
因此活化函数取非负的:
(9)
定义E(k)为性能指标函数,即:
(10)
采用最速下降法的权值进行修正,有
(11)
通过以上分析,推导出隐含层权系数:
(12)
神经网络的输出层权系数:
(13)
1.3 遗传算法控制器
虽然BP神经网络对非线性的系统有着较强的映射能力,但是该方案仍然存在不足,BP神经网络求出的为局部最优解,通过上述方法对权值修正时,易陷入局部最小化。因此,本文提出采用GA算法优化PID参数,它能够求出全局最优解,不会陷入局部最小值,且具有较强的鲁棒性。
遗传算法整定PID是指利用遗传算法中的寻优技术,对PID控制器的比例积分微分三种参数进行全局搜索,以便更有效地获得最优的PID参数[10]。与传统的控制相比,遗传算法可以在不给定KP、Ki、Kd三个参数的情况下寻找最优值,并且克服了时间过长的缺点。遗传算法整定PID参数的控制系统图如图3所示。
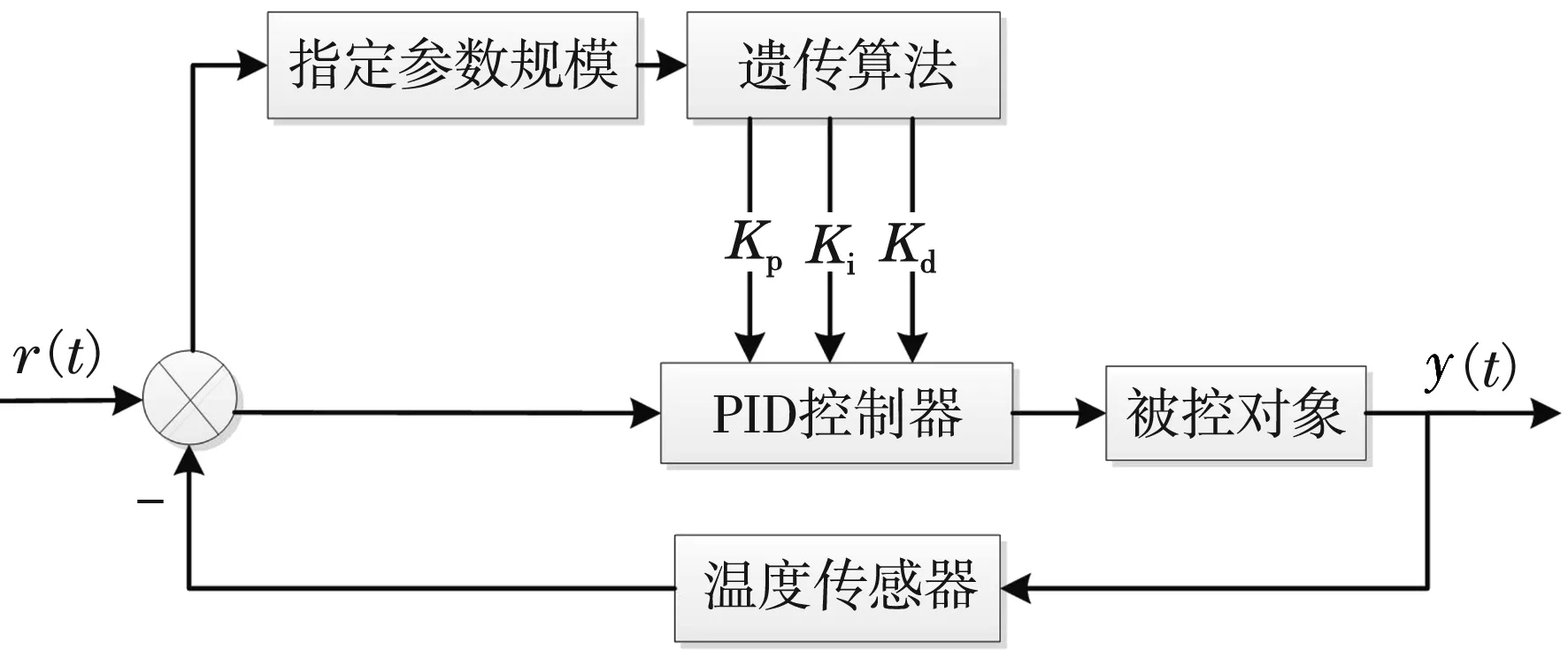
图3 GA-PID控制系统图
遗传算法的整定原理为
(1)首先确定参数范围,该范围一般是由用户给定,然后由精度的要求,对其进行编码。在利用遗传算法进行寻优的时候,需要先将被寻优问题的参数按照规则进行编码变成GA算法可以处理的方式,常见的方法有:二进制编码、浮点数编码等。本文选取二进制编码。
(2)随机产生n个个体构成初始种群。初始化种群大小的选取十分重要,过大或者过小的初始种群会影响一个算法的好坏和效率,一般实际种群大小取20~100,本文选取30;遗传代数一般取100~500,本文选取100。
(3)适应度函数的选取,合适的适应度函数可以使比例、积分、微分的参数达到最优,是PID控制系统性能评价的重要指标。在实际的问题中,一般存在两种情况:一是求出目标函数的全局最大值,二是求出目标函数的全局最小值。根据情况的不同,分别讨论适应度函数F(x):
①求全局最小值时
(14)
若f(x)<0时,
(15)
②求全局最大值时
(16)
(4)应用复制、交叉和变异算子对初始化的种群进行操作,产生新的种群。在实际应用中,交叉算子的设计会根据被寻优问题的变化而变化,常用的方式有:单点交叉法、两点交叉法、均匀交叉法。与交叉算子类似,变异算子是一种以特定的概率引起的遗传变异,产生新的种群,但是由于交叉算子具有全局搜索能力,占据主要作用,因此为主要算子,变异算子为辅助算子。
(5)重复选取适应度函数,并对新的种群进行(4)的操作再次产生新的种群,直到参数收敛或者达到期望值。
2 遗传算法控制器仿真
本文建立的GA-PID控制器与BP-PID控制器均在MATLAB上进行的仿真试验,得到的参数为Kp=6.386 7,Ki=0.493 2,Kd=0.319 3。系统运行后可以得到如图4所示的结果。
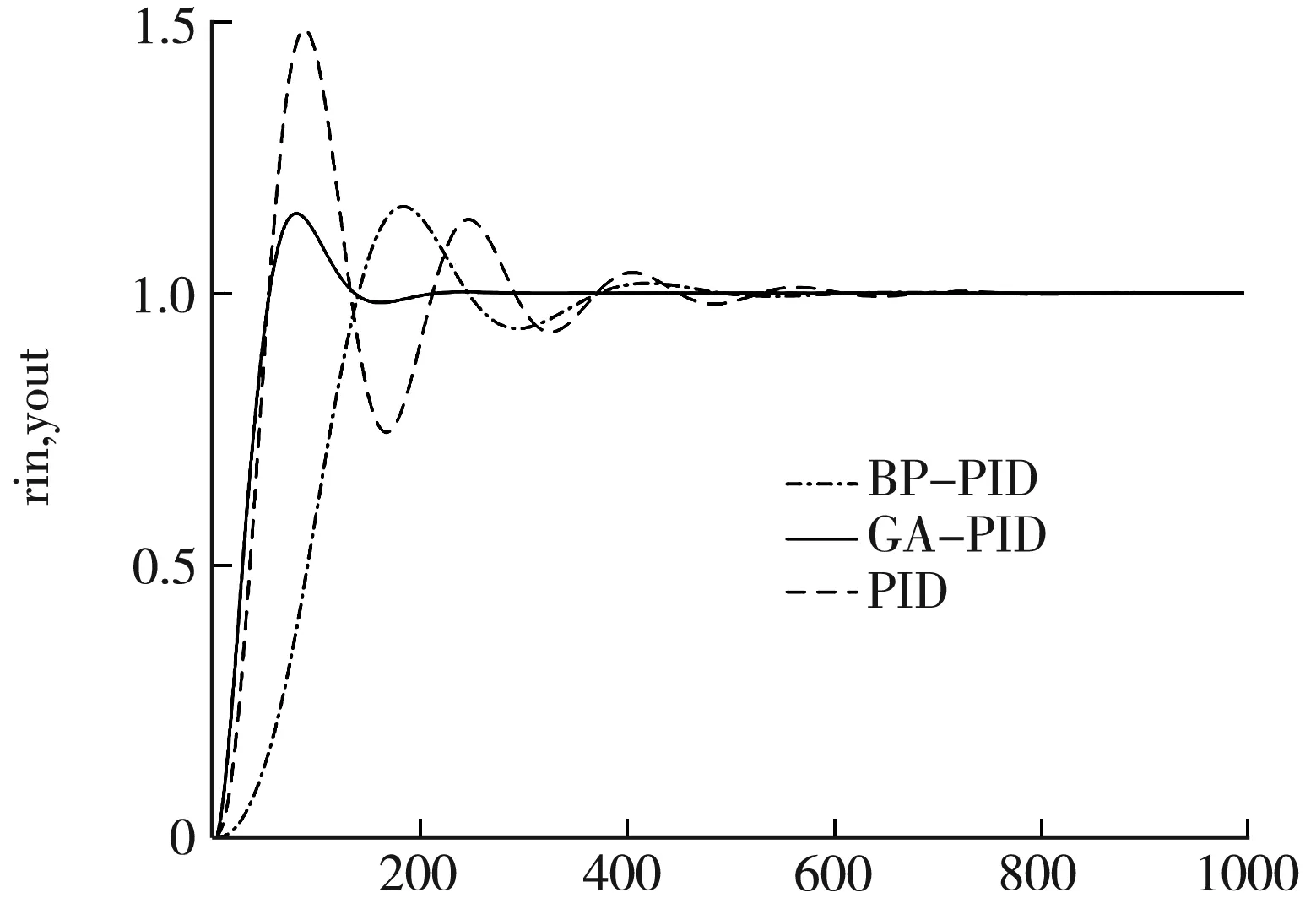
t/s图4 仿真对比图
通过图4可以明显看出,GA-PID的仿真曲线超调量较BP-PID和经典PID控制器要小,调节时间更短,曲线波动更小,控制性能更好。
3 结 论
通过3种控制方案仿真对比可以看出,遗传算法控制效果要比BP神经网络算法和传统控制系统好,它不需要预先设置初始参数值,仍旧可以找到最优的参数,并且满足了系统的性能指标。从图4中可以看出遗传算法控制器具有快速性、稳定性等特点,达到了预期目的,控制效果有了明显的提高,具有一定推广价值。
