基于浮点数的Cholesky 分解FPGA 实现*

朱 鹏 叶树霞 杨晓飞

（江苏科技大学电子信息学院 镇江 212003）

1 引言

求解逆矩阵的方法有许多，如高斯消元，矩阵分解等方法。通过矩阵分解实现矩阵求逆的运算量小且易于实现，在实际工程中被广泛运用。常用的矩阵分解方法有Cholesky分解、LU 分解和QR 分解。其中，Cholesky 分解适用于共轭对称正定矩阵；LU 分解适用于顺序主子式不为0 的任意矩阵；QR分解适用于任意矩阵。针对协方差矩阵的共轭对称厄米特（Hermitian）正定的特性，使用Cholesky分解可以节约FPGA资源使用，提高运算速度［1～3］。

本设计采用了浮点数来实现Cholesky 分解，相比定点数浮点数在运算过程中无需考虑截位效应带来的精度损失，大大提高了结果的精度。在计算浮点数开方运算上，设计了基于平方根倒数方法的硬件电路，相比传统的牛顿迭代法，大大减少了迭代次数。

2 Cholesky分解

Cholesky 分解矩阵方法是利用协方差矩阵R厄米特（Hermitian）正定的特性，将协方差矩阵R分解为上/下三角矩阵G及其共轭矩阵的乘积。通过求取上/下三角矩阵的逆矩阵的共轭矩阵GH及矩阵G的乘积，即可得到原协方差矩阵R的逆矩阵［4～5］。

R是共轭对称厄米特（Hermitian）正定，R=G*GH是矩阵的Choleksy 分解，其中G是一个具有正的对角线元素的下三角矩阵［6～7］。

由式（1）可得：

整理式（2）可得递推式：

3 平方根倒数

平方根倒数方法（Fast inverse square root），经常和一个十六进制的常量0x5f3759df 联系起来。该算法被用来快速运算平方根倒数，在20 世纪90年代末由硅图公司开发出来，后见于John Carmark的Quake III Arena的源码中。

首先在IEEE 754 标准下的单精度浮点数表示如图1。

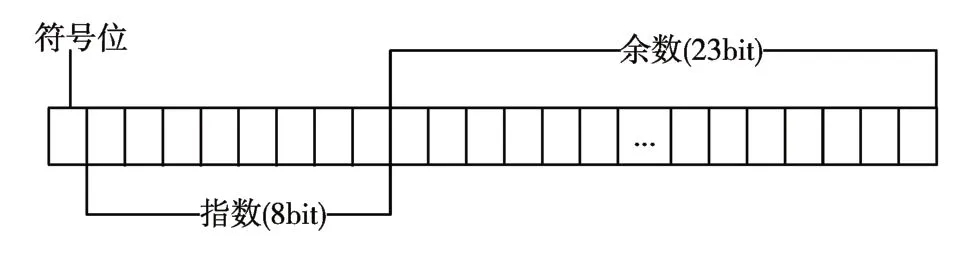
图1 单精度浮点数表示格式

由已知：

其中，ex表示浮点数的指数大小，mx表示浮点数的余数大小。

定义：Sx为符号位，当x 为正数是0，负数为1。Ex=ex+B为偏移指数，B=127 。Mx=mx+L，L=223。

在实数域中，被开方数为正数，则Sx=0。对式（4）作以2为底的对数运算得到：

因为mx∈[0，1)，所以有

其中，α为调节精度近似值。当α=0.0430357 时，可得最优结果。

根据式（5）和式（6）：

这个数可以表示为

由式（8）可得：

平方根倒数方法最重要的一步就是找出了一个迭代初值，推导出的初值越接近真实结果，算法也就收敛越快。

将式（8）的结论带入得

将数据带入式（11），并转为十六进制的：

在得到迭代初值后，只需要进行牛顿迭代法就能得到平方根倒数。

迭代公式如下：

综合式（13），式（14）得到：

在实际工程中，由于加入了平方根倒数的方法求初值，一次迭代就可以基本所需要的平方根倒数。

4 Cholesky分解模块设计

实现Cholesky 分解模块，需要一个数据控制模块和一个Cholesky分解计算模块，如图2。

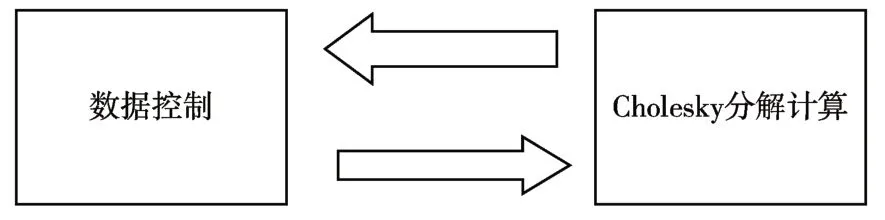
图2 Cholesky分解模块总体结构

由于协方差矩阵为共轭对称正定，所以FPGA的ram 只需要存储一半元素和主对角线元素。数据控制模块储存这些数据，并按要求发送给Cholesky分解计算块，同时接收和储存Cholesky分解出来的G 矩阵。数据控制模块数据的发送接收流程，如图3。

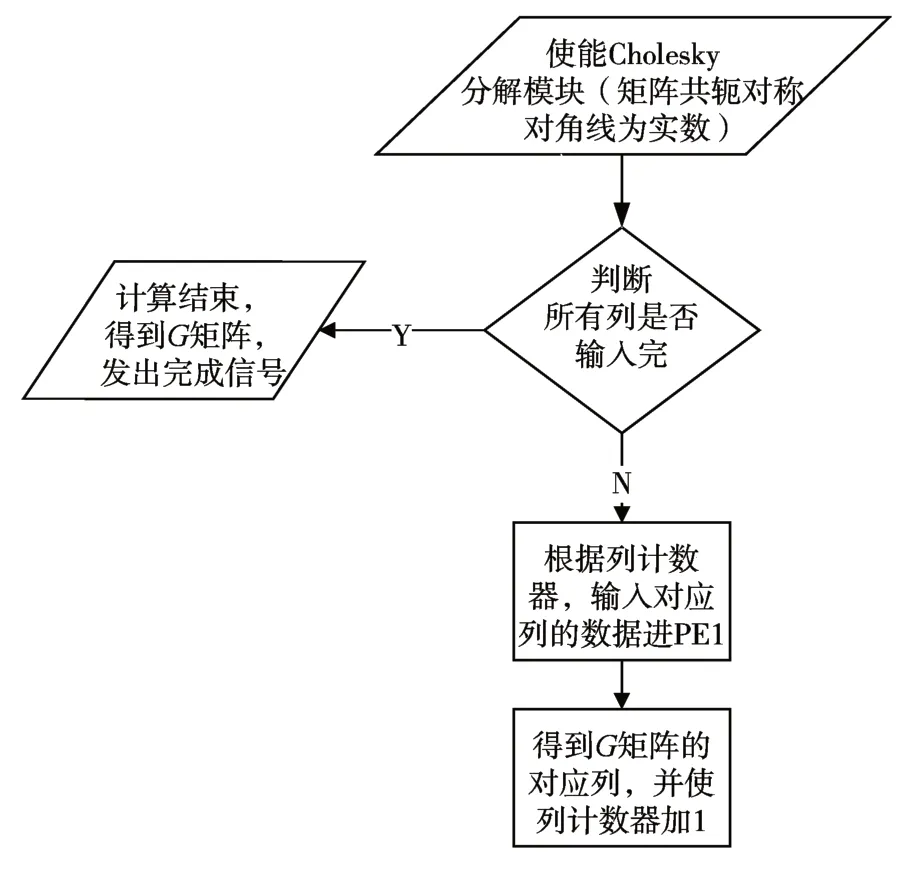
图3 数据控制模块工作流程

4阶Cholesky分解计算模块，如图4。

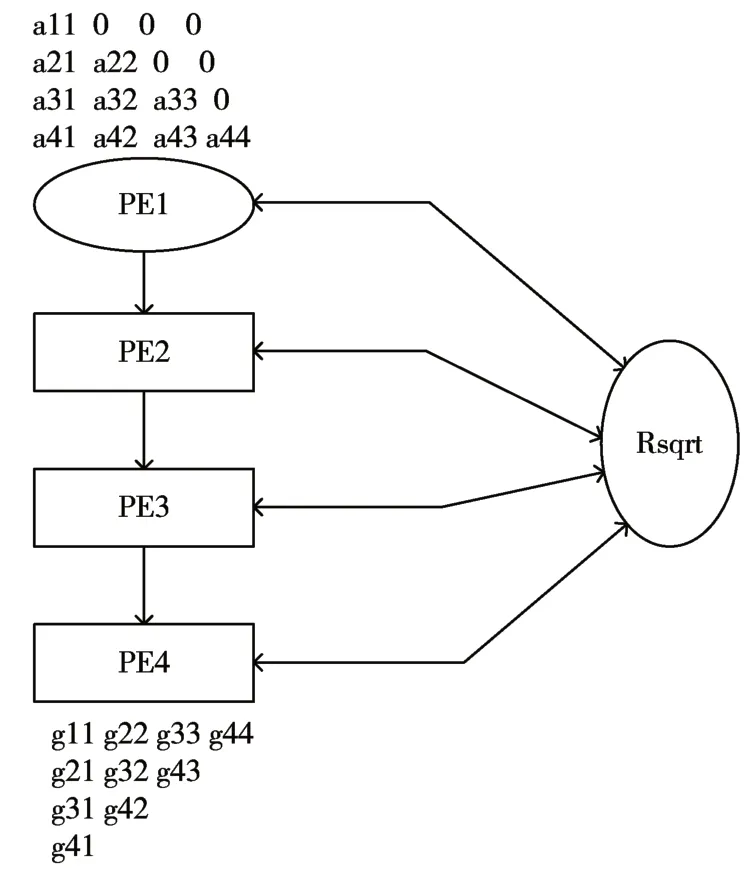
图4 4阶Cholesky分解计算模块结构示意图

因为Rsqrt 模块为求平方根倒数模块，所以主对角线元素g11，g22，g33，g44为是实际值的倒数，但是在Cholesky分解之后所作的高斯消元法、下三角矩阵求逆都需要的主对角线的倒数，可以节约后续开发资源使用［8～11］。由于每一列的Cholesky分解计算，每列只有首位元素需要求解平方根倒数，为了节约FPGA的资源，只需要一个Rsqrt模块。

如果更高阶的Cholesky 分解，只需要例化对应的PE 模块，并设置好对应位置的参数，将其于Rsqrt模块相连即可。

其中PE1 只需要计算平方根倒数为一个特殊节点，其余PE结构如图5。每一个PE节点，包含一个复数的浮点数乘法器、一个复数的浮点数加法器和存储数据的Ram。为了节约资源，当需要作减法时，只需要将减数的符号位取反，送入浮点数加法器。存储数据的Ram也是基于参数化配置，根据式（3），靠后的PE 节点需要储存前面PE 节点计算的结果，所以当前PE 节点需要前一个PE 节点加一的Ram 资源。复数的浮点数乘法器和复数的浮点数加法器都为流水线型，提高运算效率。

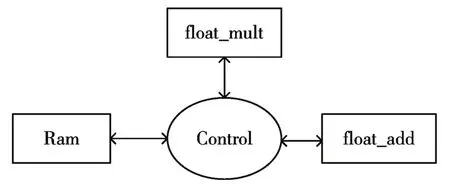
图5 PE的内部结构

Rsqrt 模块结构如图6。综合式（11），式（15）U1为一个预处理单元，其中，U1_y=0x5f3759df-(Fx≫1)。利用浮点数的性质，求F 的一半，只需要对其阶数加1。U2为一个定制单元用来计算U2_x= .5*U1_x。U3也是一个定制单元用来计算U3_x=U1_x*U1_y*U1_y。最后U4为一个浮点数减法器F_rsqrt=U2_x-U3_x。Rsqrt 模块是一次迭代的平方根倒数方法实现，流水线型实现，4 个时钟周期就可以得到输入值的平方根倒数。

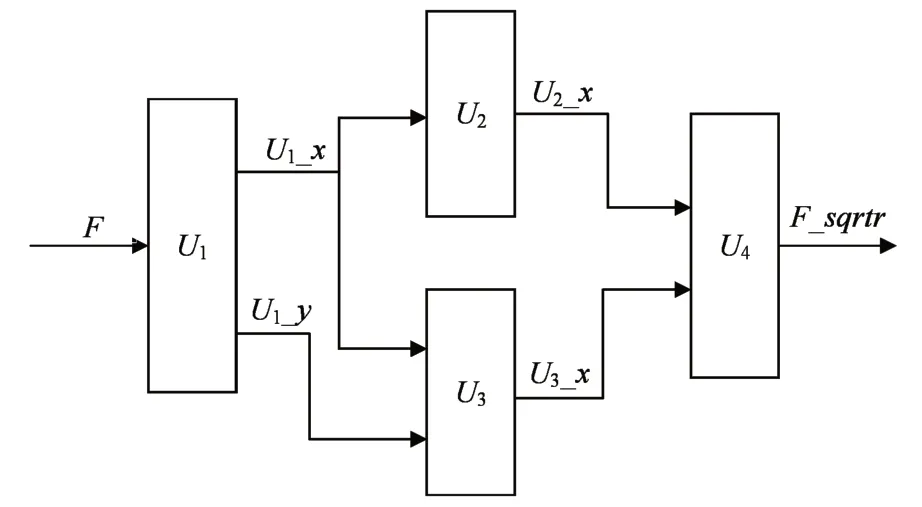
图6 Rsqrt模块的结构

5 结果分析

完成算法设计之后，对算法的可行性进行验证。本文所使用的开发环境为Vivado 2018.3，使用的硬件编程语言为Verilog HDL，实验平台是Xilinx的Xc7k325t。

实验对4 阶、5 阶、6 阶、7 阶和8 阶的Cholesky分解模块进行了仿真测试。每次实验通过Matlab［12］随机生成20 组信号协方差矩阵，将生成的数据通过coe 文件保存到FPGA 的rom 里，再将FPGA 运算好的数据通过串口读出。FPGA运算的数据与Matlab 运算数据进行比较，结果如表1 所示。运行周期为1组数据需要的运行时长，结果精度为20组数据的平均精度［13］。

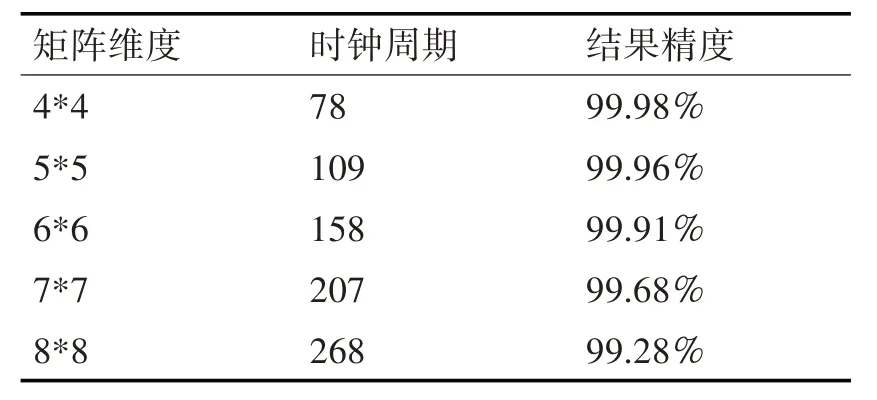
表1 实验结果

在Vivado 中，通过时序分析PE 模块在4 阶的情况下主频率可达186MHz，随着矩阵阶数的提高会逐渐降低。实验均在150MHz的主频下进行。

6 结语

本文提出了一种协方差矩阵的Cholesky 分解的并行算法和相应的硬件结构，并使用FPGA 进行了实现与验证。相比传统Cholesky 分解实现方法使用定点数相比，本文采用的浮点数精度更高，不会丢失小数位便于后续处理。采用模块化，通过PE 节点配置参数就能快速实现更高阶的Cholesky分解算法，相比全并行结构在高阶配置和资源消耗更有优势［14～15］。