双目视觉手眼标定的精度优化*

岳有军,李勇飞,赵 辉,王红君

(天津理工大学 a.天津市复杂系统控制理论与应用重点实验室;b.电气工程与自动化学院,天津 300384)

0 引言

聚晶金刚石复合片钻头(polycrystalline diamond compact bit,PDC)是一种强度、耐磨性、韧性、各向同性都极佳并且导热率也相对较好的一种钻井工具,适用于软地层和中硬地层,被用来作为石油行业的钻井工具,极大地提高了钻井速度和破岩效率,使得钻井周期大大减小。但PDC钻头在复底层钻井中经常有磨损严重、掉齿、崩刃、复合片脱落等现象发生,这造成了钻头寿命降低甚至失效的结果[1]。PDC钻头造价昂贵,需要采取保护措施,延长钻头的寿命。目前的采用的方式是在PDC钻头受力和齿磨损最大的胎体冠状部堆焊一层碳化钨,提升其耐磨性[2]。为了确保钢体钻头的敷焊成品质量,使用双目视觉焊接机器人对其进行表面敷焊,敷焊对机械臂定位精度要求极高,为了提高定位精度,对Eye-To-Hand型手眼标定方程的求解进行了算法优化研究。

费致根等[3]采用了非线性优化算法Adam优化手眼标定矩阵,其非线性算法的精确度优于线性算法,但并未解决奇异解问题且容易陷入局部最优解;李巍等[4]用四元数参数化旋转矩阵,LMI凸松弛化全局的方法解决了非线性算法容易陷入局部最优解的问题,但精度并没有明显的提升;马清华等[5]用矩阵直积法计算出了手眼标定矩阵,以最小化重投影误差为代价函数优化了手眼标定矩阵,该方式具有良好的稳定性和准确性,但以复杂繁琐的重投影误差函数作为代价函数,迭代速度慢,标定过程耗时过长;TSAI等[6]使用一种线性算法,将旋转和平移分开计算极大地提高了计算效率,标定速度极快,缺点是只有一组数据参与,容易被偶然误差影响,导致精度不高。王龙等[7]提出一种基于LMI优化的对偶四元数手眼标定算法,用线性矩阵不等式代替了奇异值分解法,最后通过实验证明了精度有所提升,同样计算过程复杂,迭代效率低。吴庆华等[8]基于矩阵奇异值分解求取手眼标定矩阵,但在数据测量时需要先变换θ角,判断测量数据是否可以用于标定,提高了标定精度,但需要先判断数据是否可用。

针对目前线性算法容易受到偶然误差干扰,非线性算法容易陷入局部最优解以及奇异解的问题,提出了一种全新的方法,以眼在手外作为试验平台,解决了手眼标定矩阵AX=XB在使用Ada-delta过程中的梯度的求取问题,在线性算法求解AX=XB的基础上引入非线性算法,利用线性算法确定性的结果解决和改善了非线性算法奇异解和局部最优解的问题,利用非线性算法多数据的优势避免了线性算法容易被偶然误差影响的问题。Ada-delta具有自适应的学习率,不易陷入局部最优解,用于求AX=XB具有稳定性较强,抗干扰能力好,精确度更高的特点。

1 双目视觉空间定位原理

双目视觉定位本质上是利用视差获取距离信息,利用相平面坐标获取位置信息。如图1双目相机是利用左右相机与标定点构成两个底边共线的三角形,通过这两个三角形之间几何变换关系求取标定点相对于双目相机的位置,获得标定点在相机坐标系的三维坐标[9]。

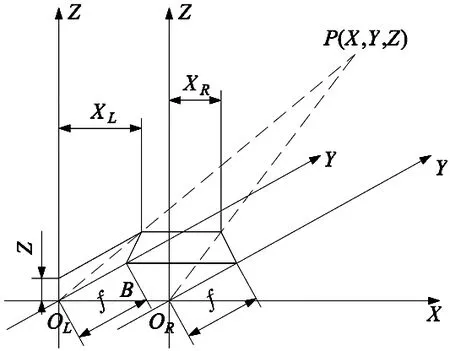
图1 双目成像原理

根据三边平行,两三角形相似,可以由相似三角形的性质得到点在相机坐标系的三维坐标与其在相平面成像点坐标的关系式:

(1)

式中:(xL,z)和(xR,z)分别为点在左相平面和右相平面的成像点坐标,f为相机的焦距,B为基线,(X,Y,Z)为点在相机坐标系中的三维坐标[10]。

可以看出计算是默认双目相机X轴共轴,Y、Z轴平行,但在实际装配中几乎不可能做到这点,同时相机镜头在制造过程也会不可避免的产生误差,镜头误差产生的径向和切向畸变会使理论成像点与实际成像点落点不同。所以通过拍摄多张标定板图片,对左右相机在同一时刻拍摄的图片进行纵横向对比,可以得到左右相机坐标系之间的相对位姿关系,以及切径向畸变数据,即可修正左右相机之间的装配误差以及镜头本身的误差[11]。

2 手眼标定模型

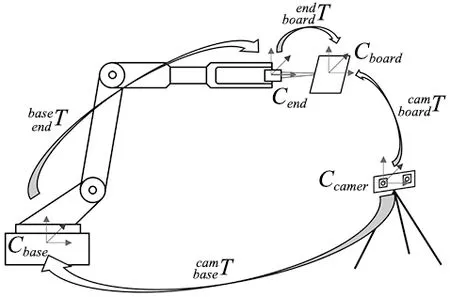
图2 手眼标定模型

(2)

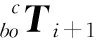
(3)

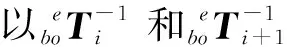
(4)

(5)

利用这一点联立式(4)、式(5)可得:

(6)

(7)

令:

则式(7)就是AX=XB,只需求A、B的值就可得到机械臂基坐标系相对于相机坐标系的位姿转换及矩阵X[13]。

可以分别转化为:

(8)

(9)

由式(8)、式(9)可以看出A、B分别为标定板坐标系在相机坐标系、机械臂末端坐标系在基坐标系第i到i+1次的位姿转换矩阵,所以A可以从相机外参获取,B可以直接读取机械臂末端位姿获得。

3 优化算法

Ada-delta是非线性算法,非线性算法的优点是可以通过大量的样本数据计算获得高精度的结果,其本质上是通过求变量的梯度,然后反向传播来向最低点前进,通过多次迭代最终到达最低点[14]。而Ada-delta算法在这个基础上增设了自适应学习率,能够根据损失函数的梯度比值变化而自主调节学习率,确保了在开始迭代时的学习率稳定变化,以及迭代末期学习率不会太小导致迭代效果差[15]。在迭代计算中,每一步迭代的内容是最耗费时间的,所以为了提高整体的效率,将4×4的位姿转换矩阵分成旋转矩阵和位姿矩阵两部分进行计算,先利用Ada-delta计算3×3的旋转矩阵,然后利用已知的旋转矩阵带入到Ada-delta中求位移矩阵。使用Ada-delta求解AX=XB的最大问题是全矩阵运算式是无法求梯度的,针对这一点提出了一个解决方案,那就是将矩阵的元素分开求取,令,

HR(X)=ARXR-XRBR

式中:HR为姿态转换矩阵,AR为标定板两次姿态之间的变换矩阵,BR机械臂两次姿态之间的变换矩阵。

则

(10)

式中:HR(ω)全为0,可以得到:

(11)

由式(11)可看出只需要计算hR11、hR21、hR31就可以计算出所有的ω值,从而求出XR。

求平移矩阵需要将已知的旋转矩阵带入到位姿转换矩阵的方程AX=XB中,得到同式(10)的方程组,由于旋转矩阵已知,只需要求其中一个式子h14就可以得到平移矩阵的值。

h14=a11ω14+a12ω24+a13ω34+a14ω44-
b14ω11-b24ω12-b34ω13-b44ω14

(12)

式中:ω14,ω24,ω34组成分别为平移矩阵的XYZ值,根据位姿矩阵的组成X可知ω44的值为1。

(13)

将hR式带入到Ada-delta中去迭代时,方程中没有非零的常数项,显然解不是唯一的,会产生通解和奇异解。将线性算法求出ω的初始值ω11,ω22,ω33代入到式(11)中,保证每个h都有两个常数项,以避免通解和奇异解的出现,并且不会因为额外引入常数项而引起误差。

Ada-delta算法是在梯度下降法的基础上进行了大量的优化变动而生成的一种能自动生成并更新学习率的优良非线性算法,适合于处理大量数据、计算梯度可求的方程。

一是全面强化顶层设计，重大研究取得明显进展。组织调研论证，梳理出七大流域40个重大水利科技问题。新增“东北四省区节水增粮高效灌溉技术研究与规模化示范”等4项国家科技支撑计划项目。“巨型机组水电站建筑结构关键技术”等4项科技成果获国家科技进步二等奖，“强涌潮河口曹娥江大闸工程建设关键技术研究与实践”等49项科技成果获大禹水利科学技术奖。

Ada-delta算法主要内容是:

建立目标函数h(ω),损失函数loss(x)为预测值减真实值的方差,设置学习率lr的更新参数S,delta的更新权重;

设置S、delte的初始值,通过对loss函数求的梯度的初始值分配权重对S、delta更新,利用更新的S、delta求得合适的学习率lr;

利用当前x对应的梯度与学习率求得ω的参数更新量,对ω进行更新,一直迭代,直到loss函数小于设定值或到达迭代次数后停止。

过程代码:

(1)设置目标函数:h(x)=x1ω1+x2ω2+x3ω3-x4ω4-x5ω5-x6ω6;预测函数:pred(x);损失函数:loss(x)=(pred-y)2;

(2)eps=0.001,更新ω=ω+eps,利用更新后的ω求loss函数,联立更新前后的loss函数计算梯度:gradient=(loss_after-loss_before)/eps;

(3)令S、delta的初始值为0,更新权重设置为0.2,0.8,S=0.2*S+0.8*gradient2;lr=(delta+1×10-6)/(S+1×10-6);分子分母添加1e-6是防止初始的学习率为0;

(4)参数更新量:gradient_ω=lr1/2*gradient;ω=ω-gradient_ω;

(5)用更新后的ω更新delta放到下一次迭代中使用delta=0.2×delta+0.8×gradient2;

(6)迭代5000次之后,得到ω的值,就可以进行下一个h式的计算。

4 仿真实验验证

4.1 双目相机参数标定

本次实验使用的双目相机模组尺寸为38×38 mm,可输出图片像素最大为1924×1080,焦距6 mm,基线80 mm。手眼标定之前需要先对相机进行参数标定和修正。使用OpenCV的16×16 mm棋盘格标定板,角点为11×8,拍摄约50组标定板图片。

(a) 左相机图片 (b) 右相机图片图3 标定图像

标定结果如表1和表2所示。

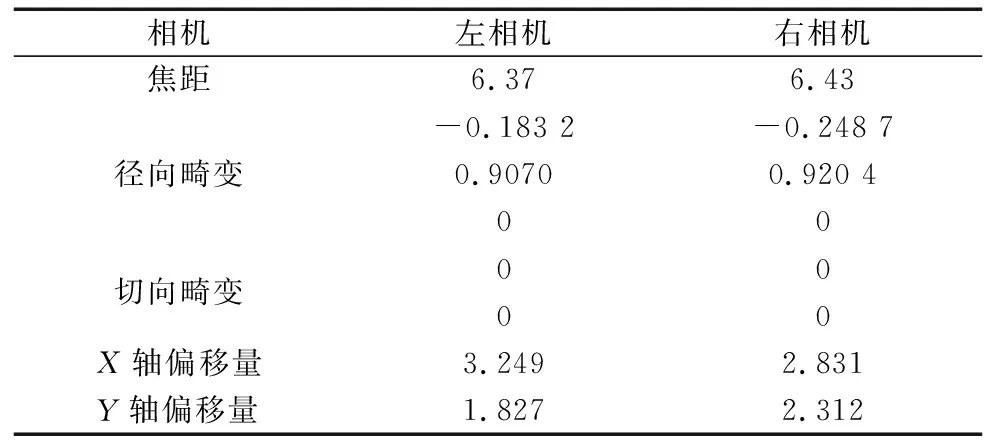
表1 双目相机内部参数 (mm)

表2 双目相机外部参数

使用MATLAB内置的stereo Camera Calibrator计算得到相机标定误差为0.11 pixel。

图4 标定板角点检测

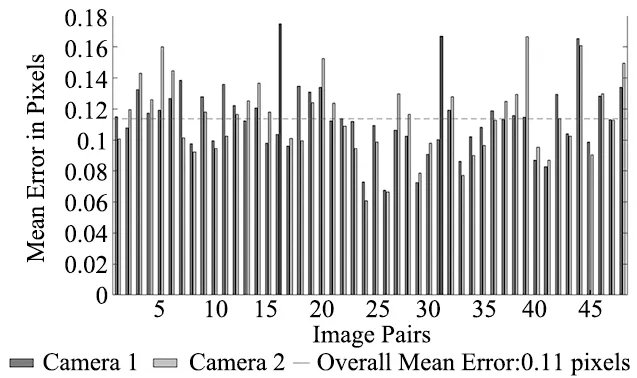
图5 双目相机标定误差

4.2 手眼标定

本次实验使用的是双目相机与机械臂分离且相对位姿确定的眼在手外型布置,实验平台如图6所示。

图6 手眼标定平台

非线性算法需要大量的数据支撑计算,因此测取了59组手眼位姿的数据,对其用排列组合的方式扩充,共有58×59=3244组基础数据。

4.3 数据结果比较

将数据代入到Tsai中,得到位姿转换矩阵:

最终得ω11=-0.512 2,ω22=0.942 9,ω33=-0.525 9,将ω11,ω22,ω33代入非线性方法Ada-delta中,迭代5000次,随着迭代次数的递增,3个方程的损失函数及原函数最终都趋向于0,得到旋转矩阵:

将旋转矩阵带入到位姿矩阵的求解方程中,迭代5000次,得到位姿矩阵:

由式(2)变换得:

(14)

将优化前后的X代入,再代入手眼对应的一组数据可以得到优化前后的标定板和机械臂末端的位姿关系。

式中:T1、T2分别为通过优化前和优化后的X解得的标定板和机械臂末端的位姿转换关系矩阵。

将优化前后的X与获得的T1、T2联合代入相机与标定板的位姿关系求出机械臂末端在机械臂基坐标系中的理论位姿,与机械臂系统读取的真实位姿作差得到一个差值矩阵,然后对差值矩阵的每个元素取绝对值求和,选取了15组数据进行比较,比较结果如图7所示。

图7 优化前后的Frobenius范数

优化前的差值矩阵平均值为0.305 65,优化后的平均值为0.520 717。

5 结论

在传统手眼标定算法中,线性算法由于只需一组图像数据,计算速度快,但同时容易受到偶然误差的影响。非线性算法有大量的基础数据做支撑,具有高精准度、抗干扰能力强的优点,但容易陷入局部最优解,并且由于方程AX=XB没有常数项,会面对奇异解的问题。

将线性算法Tsai与非线性算法Ada-delta结合,先将一组数据带入到Tsai中求解AX=XB,得到优化前的手眼标定矩阵X,然后将X中的3个对角线元素ω11,ω22,ω33带入到Ada-delta算法中,求解出X其余的元素,得到优化后的X。首先,Ada-delta算法的自适应学习率在很大程度上避免了局部最优解问题;其次,在非线性算法中引入了常数项,避免了产生奇异解的问题;最后,大量图像数据作为运算数据的支撑,增强了算法的抗干扰能力和鲁棒性,避免了偶然性误差的影响。

实测结果也表明,基于Ada-delta的优化算法得到的手眼标定矩阵的精度比传统线性算法得到的精度更高,且一致性较好。