同轴度法标定相贯线工件坐标系*

陈 琳,李权文,付 钰,李松莛,潘海鸿,黄龙鹏

(1.广西大学机械工程学院,南宁 530004;2.广西工业技师学院机械系,南宁 530007)

0 引言

相贯线工件是一种拥有复杂空间曲线的工件,广泛应用于石油、化工、供热、消防等领域,相贯线人工示教焊接轨迹难度大,耗时耗力,同时人工示教的示教点往往不均匀,不利于机器人和变位机进行轨迹插补[1-2]。所以,相贯线工件坐标系的标定决定了离线编程时相贯线轨迹规划的准确性。研究人员关于机器人与工件坐标系的标定方法进行了大量的研究工作,其主要方法可分为两类:附加测量设备标定法和固定基准点标定法。

(1)附加测量设备标定法:周祥[3]采用了基于高精度位置传感器(PSD)的工件坐标系标定方法。将PSD传感器装在2自由度云台上进行了工件坐标系标定实验,实际测试的标定精度较高。林巨广等[4]提出一种利用百分表位移测量装置对工件坐标系的标定方法。ZHANG等[5]提出一种使用气压传感器和激光传感器工件姿态估计的工业方法。(2)固定基准点标定法:田啟良等[6]提出了一种快速标定工件坐标系的方法。首先在工件上建立合适的工件坐标系用于标定,然后控制焊枪移动到工件上不共线的3个点,记录焊枪的位姿信息,最后通过工具坐标系间接求出工件坐标系与机器人基坐标系之间的位姿变换矩阵。LU等[7]提出一种双机器人系统中工件坐标系的自动同步方法,通过测量3个非共线标定点的坐标值来实现两个机器人基坐标系之间的变换。LIU等[8]提出了一种利用双机器人对工件坐标系进行标定的方法。通过测量工作空间中任意3个非共线点的坐标值,计算得到两个机器人基坐标系之间的平移和旋转矩阵。

针对以上研究中存在的标定步骤复杂,精度不高的问题,提出一种使用同轴度法标定相贯线工件坐标系,该方法建立相贯线工件坐标系模型;标定过程中均匀采集相贯线工件上的标定点,并考虑不同方位的误差影响;使用遗传算法[9]求解出最优轴线方向向量,最后实现相贯线工件和机器人基座标系之间的位姿标定。

1 相贯线工件坐标系建立

相贯线工件是由两个独立的圆柱管相交所组成的工件,一般将横向放置的圆柱管称为主管,将竖直放置的圆柱管称为支管。对于一般形式的相贯线工件通常用主管半径R、支管半径r、偏心距σ和相贯角δ表示。由于两个管轴线的公垂线与主管轴线和支管轴线分别交于一点(图1),将这两点分别定义为主管坐标系原点O1和支管坐标系原点O2。在主管坐标系{O1}中,将竖直向上的方向定义为主管坐标系Z轴正方向;水平向右定义为主管坐标系Y轴正方向;X轴方向可由右手螺旋定则判断出。同理建立支管坐标系{O2}。

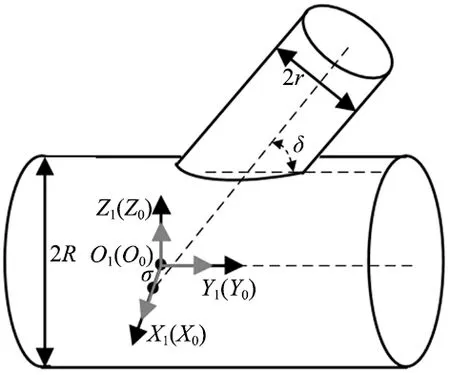
图1 通用相贯线工件坐标系

2 基于同轴度法的相贯线工件坐标系求解

建立相贯线工件坐标系前,需首先确定主管和支管坐标系,而主管和支管坐标系的建立首先需要确定主管和支管的轴线。通过机器人TCP点分别在主管和支管上各取3个标定点,根据3点确定一个圆,求解出空间圆的圆心,同时也可求解出空间平面的法向量;通过法向量与圆心即可求解出圆柱的轴线方程。但是在实际焊接加工过程中,会存在以下3个误差:①主管和支管在加工过程中会存在加工误差,使得主管和支管都不是标准的空心圆柱体;②在主管和支管上各取3个标定点时,存在测量误差;③实际测量情况很难保证3个点所确定的平面和轴线垂直,此时以空间圆代替空间椭圆也会造成计算的误差(图2)。因此,提出一种基于同轴度法的机器人与相贯线工件坐标系标定方法。

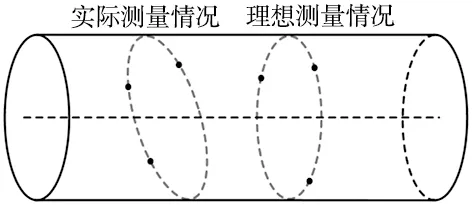
图2 测量点位置误差

2.1 同轴度法计算空间圆柱轴线方程

假设相贯线工件主管的轴线记为l1,且轴线的方向向量为(l,m,n),显然方向向量应满足:

l2+m2+n2=1

(1)

假设轴线l1过点S0(x0,y0,z0),圆柱管上的标定点的位置坐标记为Si(xi,yi,zi),1≤i≤k。根据空间两点的距离公式可知,S0和Si的距离di大小为:

(2)

S0和标定Si可确定空间向量S0Si,可表示为(xi-x0,yi-y0,zi-z0),1≤i≤k。

图3为测量点距离计算模型,在图3中空间向量S0Si与轴线l1在空间中存在夹角,假设夹角记为αi,1≤i≤k,夹角的余弦值大小为:

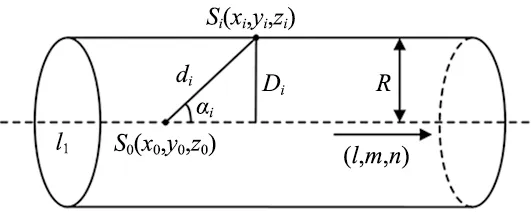
图3 测量点距离计算

(3)

将式(1)代入式(3)中得到式(4):

(4)

标定点Si到圆柱管轴线l1的距离Di大小为:

(5)

将式(4)代入式(5)中得到式(6):

(6)

假设主管圆柱半径为R,因误差的不可避免,Di与R的值会存在偏差,需在空间中找出最优轴线作为主管轴线(图4)。在该轴线上,所有Di与R距离的和达到最小,即使得式(7)的值最小。

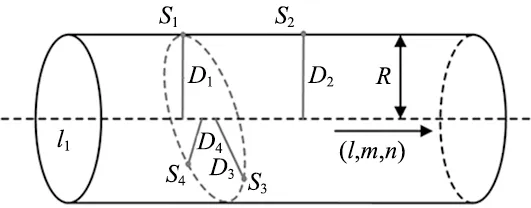
图4 同轴度法拟合圆柱轴线

(7)

求解式(7)的最小值属于非线性函数求最值问题,使用遗传算法进行求解。

式(7)出现根号以及绝对值运算,计算的复杂性不适合作为适应度函数。可考虑用平方运算代替根号和绝对值运算,因此使用式(8)作为遗传算法的适应度函数。

(8)

使用遗传算法可计算出最优x0、y0、z0、l、m、n和R的值,此时轴线l1的方程为:

(9)

2.2 机器人与相贯线工件坐标系位姿变换矩阵求解

(10)

假设l1和l2的公垂线为l,其方向向量为(L,M,N),且过点S(X,Y,Z)(图5)。方向向量(L,M,N)也为相贯线工件坐标系X轴的方向向量,(l,m,n)为相贯线工件坐标系Y轴的方向向量,根据右手螺旋定则可确定相贯线工件坐标系Z轴的方向向量。

图5 通用相贯线工件坐标系方向向量求解

根据空间直线方程的定义,公垂线l的方程可表示为:

(11)

根据公垂线的定义,l1与l2均和l垂直,所以直线l的方向向量可由直线l1的方向向量与l2的方向向量叉乘算出。因此,直线l的方向向量为:

(L,M,N)=(mn′-nm′,nl′-ln′,lm′-ml′)

(12)

因为公垂线与其中任何一条轴线都是共面的,根据共同面内三条直线行列式为零这一基本定理,可得式(13)和式(14):

(13)

(14)

点S(X,Y,Z)是直线上任意一点,取X=1,由式(13)和式(14)可求解出Z和Y的表达式为:

(15)

(16)

图5中相贯线工件坐标系的原点O0为直线l和l1的交点,假设原点O0坐标为(O0x,O0y,O0z),由空间两直线的交点公式,计算出O0x、O0y和O0z的表达式为:

(17)

支管坐标系原点O2为直线l和l2的交点,假设O2坐标为(O2x,O2y,O2z),根据空间两直线的交点公式,可计算得出O2x、O2y和O2z为:

(18)

偏心距σ为原点O0和原点O2的距离为:

(19)

相贯角δ空间直线l1和l2的夹角为:

(20)

相贯线工件坐标系Z轴的方向向量可由(L,M,N)和(l,m,n)叉乘计算得出:

(Mn-Nm,Nl-Ln,Lm-Ml)

(21)

综合式(12)、式(17)、式(21)和主管轴线方向向量(l,m,n),机器人与相贯线工件坐标系的位姿变换矩阵为:

(22)

3 实验

自主搭建焊接实验平台(图6)主要由机器人、双轴变位机、机器人电气控制柜、双轴变位机电气控制柜、相贯线工件、工控机、示教器和控制软件组成。

图6 焊接工作站硬件图

3.1 六点法相贯线工件坐标系位姿变化矩阵

工业中常用六点法标定圆柱管件的轴线(图7),其是假设3个点在同一个圆面上,为标定的精确性,将相贯线工件竖直。在主管上取点时保持机器人末端焊枪TCP在Y方向上不发生移动,只通过移动X和Z在主管上得到3个标定点。

图7 六点法标定工件坐标系

图7a为标定主管轴线示意图,在上位机中读取主管上3个标定点坐标,如表1所示。

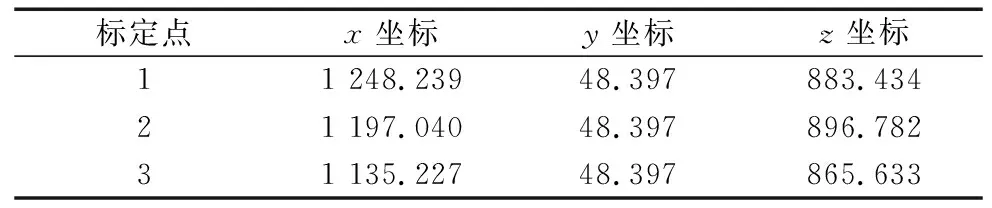
表1 主管上3个标定点位置 (mm)

三点确定主管上一个圆面,可计算出主管半径为86.572 7 mm,所确定圆心为(1201.8440,48.3970,810.3428),平面方向向量为(0.0,-1.0,0.0)。

同理,如图7b所示,得到支管上如表2所示的3个标定点坐标。

表2 支管上3个标定点位置 (mm)

计算得支管半径为69.597 7 mm,所确定圆心为(1191.8777,-37.4868,942.9770),平面的方向向量为(0.0,0.0,1.0)。

根据主管和支管的参数,由式(22)可得到相贯线工件坐标系的圆心坐标为(1201.8440,-37.4868,810.3428),相贯角δ=90.0°,偏心距σ=9.966 mm,相贯线工件坐标系相对于机器人基坐标系的位姿变换矩阵为:

3.2 同轴度法标定相贯线工件坐标系位姿变换矩阵

采用同轴度法分别标定主管和支管时不需要考虑标定点是否在一个圆平面上,因此可随意在工件表面上取点。保持变位机和相贯线工件均在初始位置,移动机器人的TCP点,使其可以触碰到相贯线工件主管上的不同位置。

如图8a所示标定相贯线主管,通过上位机软件记录10次不同的位置值,如表3所示。

图8 同轴度法标定工件坐标系

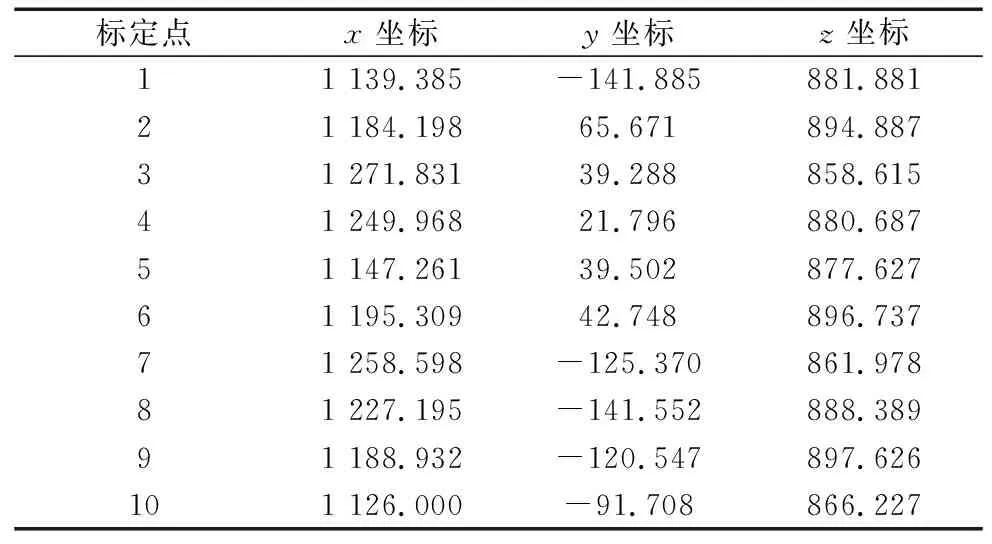
表3 主管上标定点位置 (mm)

将数据代入式(8)中,使用遗传算法求解,设x0、y0、z0、l、m、n和R的阈值为0.3,迭代收敛阈值为两次迭代间差值小于0.01。得到主管半径R=88.936 9 mm,其轴线的方向向量为(0.0219,-0.9997,0.0110),且过点(1194.54,-41.21,807.73)。

同理,如图8b所示,标定相贯线支管记录10次不同的位置值,并记录在表4中。

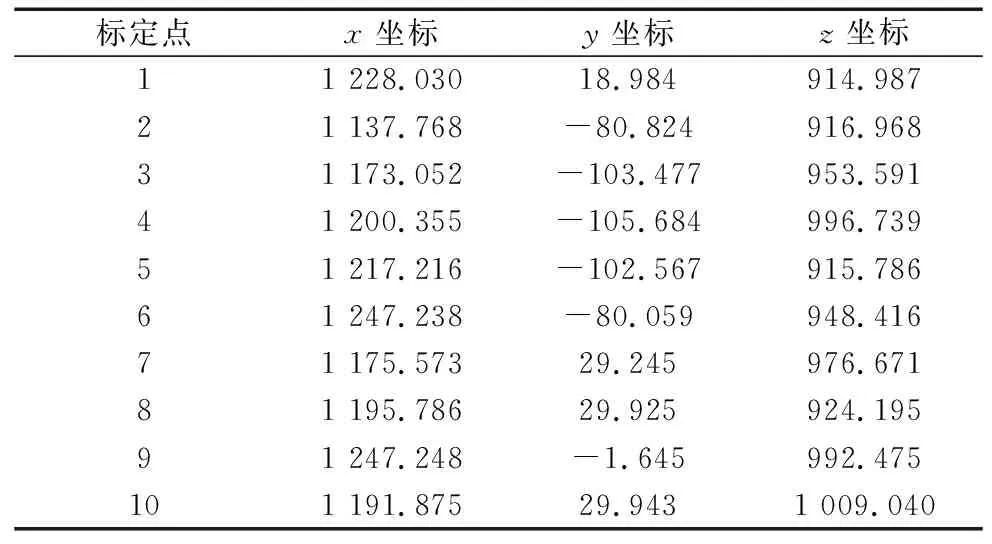
表4 支管上标定点位置 (mm)

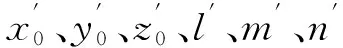
将主管和支管的参数代入式(17)、式(19)、式(20)和式(22)中计算得到相贯线工件坐标系的圆心坐标为(1191.3318,-38.4284,954.8868),相贯角δ=91.638 9°,偏心距σ=10.358 8 mm,相贯线工件坐标系相对于机器人基坐标系的位姿变换矩阵为:

3.3 精度验证与分析

在6R机器人末端焊枪上装上焊缝跟踪系统(图9)对相贯线工件上的焊点进行扫描,得到焊点在机器人基座标系下的位姿,最终验证标定得到的相贯线工件坐标系的精度。

图9 焊缝跟踪系统实物图 图10 焊缝跟踪系统扫描焊缝

在相贯线工件上取φ∈[0,π/2]区间中的焊缝,图10a为激光线扫射的起点,此时φ为0°;图10b～图10e为激光线扫射的中间点,焊缝跟踪系统与焊缝的距离大致相同;图10f为激光线扫射的终点,此时φ为90°。

表5为焊缝跟踪系统的技术参数。

表5 焊缝跟踪系统技术参数

使用焊缝跟踪系统扫描相贯线工件上的焊点,与六点法和同轴度法计算得到的焊点位置进行比较,得到结果如表6所示。

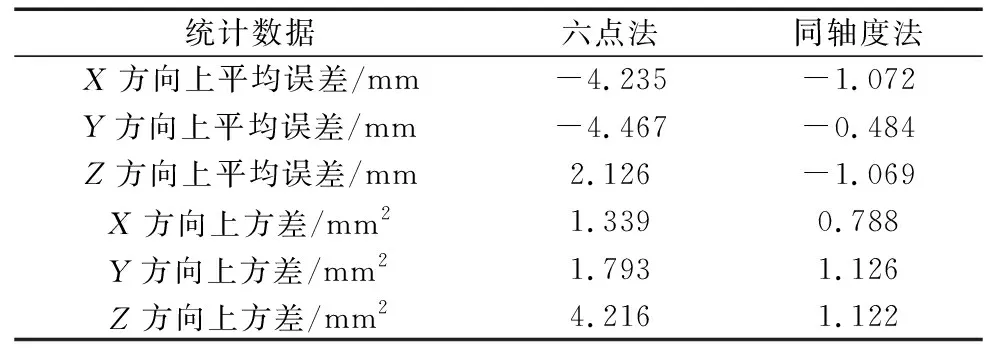
表6 两种标定方法下相贯线焊接路径精度对比

从平均误差和方差上看,基于同轴度法生成的焊接路径在X、Y和Z方向上误差均小于基于六点法生成的焊接路径,基于同轴度法生成的路径在X和Z方向上的平均误差约为1 mm。这表明基于同轴度法生成的焊接路径精度更高,数据波动也更小。

4 结论

为解决相贯线工件标定复杂,精度不高的问题,提出使用同轴度法对相贯线工件坐标系进行标定。该方法建立了相贯线工件的一般数学模型;标定过程中在相贯线工件上取点较均匀,使用同轴度法拟合圆柱轴线方程,并使用遗传算法求解出最优轴线方向向量,从而得到最优相贯线工件坐标系;在机器人与变位机实验平台进行标定实验,并通过激光跟踪系统识别的焊缝位置与同轴度法和六点法计算的焊缝位置进行对比,判定基于同轴度法生成的理论相贯线焊接路径的精度较高,证明基于同轴度法的机器人与相贯线工件坐标系位姿标定的正确性。