基于环形耦合的多电机转矩均衡控制*

牛宗贤,范 波,1b,付雨林,王春光,吴晓丹,杨晨辉

(1.河南科技大学 a.信息工程学院;b.河南省机器人与智能系统重点实验室,洛阳 471023;2.西安交通大学钱学森学院,西安 710049)

0 引言

多电机齿轮传动系统在各种工业领域中已广泛应用,并且应用范围和要求随着工业发展逐步提高。大多数工艺流程所使用的多电机传动结构为无耦合结构,即系统中的各台电机之间没有物理连接,如钢厂的连铸机、冷轧机、丝织业的染整机、拉丝机等。这类结构的特点就是系统内的电机控制参数、型号、给定信号以及控制策略全部一致,任意一台电机上发生扰动都不会影响其他电机,但是产生的同步误差会严重影响系统的运行[1-2]。

在一些特殊的场合,电机之间需要实现物理连接,通过特殊传动结构来驱动系统运行,典型的传动结构有两种,一种是柔性连接方式,电机之间通过皮带轮传动方式耦合连接,除了电机控制策略,系统同步性能还受皮带轮的张力等因素的影响,所有大型工业用传送带均采用这种方式;另一种是刚性连接方式,电机之间通过齿轮传动结构耦合连接,系统除了受电气控制因素影响,还受到齿轮结构的机械因素影响,典型的应用就是盾构机和龙门吊等。

刚性连接系统的结构特点决定了其控制方式的特点。由于齿轮的强制耦合特性,系统内的电机转速会被保持在同一速度下,但是其转矩在系统出现扰动时,就会产生较大的误差,从而导致电机转轴和齿轮组的负荷急剧增加,磨损也会随之增加,严重影响电机和齿轮的使用寿命[3-4]。于是,多电机的控制策略对转矩均衡也有了极大的要求。

对于多电机的控制策略,湖南工业大学[5]针对永磁同步电机设计了一种双偏差耦合的控制方式,同时对多电机转矩、转速进行同步控制,并且在偏差耦合控制结构中引入滑模控制方法,对该方法进行了理论分析,验证小型电机组功率平衡控制方案;刘然[6]提出了多电机环形耦合转速、转矩控制理论,并且分析和仿真验证了转速控制的可行性,由于系统内电机状态只受相邻电机的影响,所以在电机组中电机数量较多时性能优于其他控制策略,为大型多电机组同步控制提供了新的研究方向,但是多电机环形耦合转矩控制尚未验证;耿强等[7]针对双电机刚性齿轮传动结构因为机械损耗引起的转矩分配不均衡问题,提出一种基于交叉耦合控制的转矩均衡控制方式,有效减少了电机输出波动和机械损耗,降低了系统过载风险,但是只能应用于小型多电机系统;廖建峰等[8]针对盾构机刀盘的多电机驱动系统提出了一种广义非线性时变动力学模型,分析多电机驱动系统的负载变化,并提出一种集成控制的鲁棒控制器,以实现刀盘转速跟踪和转矩均衡分布;胡仙等[9]针对刚性连接的多电机系统转矩输出不均衡问题,提出一种基于功率下垂控制的转矩均衡策略,使变流器在无信号互联的情况下对两台交流异步电机进行转矩均衡控制,但此方法同样只适用于双电机系统,当电机数量增加时,系统稳定性尚需验证。

针对上述问题,本文提出一种改进的多电机环形耦合控制结构。首先,刚性连接的多电机系统由于齿轮传动作用,电机转速被强制耦合在同一速度下,所以将环形耦合转速控制结构应用于多电机的转矩控制中,针对多电机刚性齿轮传动结构建模分析并对控制参数进行调整和测试;其次,通过最大与最小转矩波动对补偿参数进行加权处理,使系统稳定性进一步优化,以降低多电机刚性结构本身引起的转矩输出波动,在发生负载突变或外部扰动的情况下,多电机系统能够平滑输出。

1 系统模型分析

在大多数多电机无耦合连接结构中,当系统出现扰动,首先影响的是各电机转速,所以此类控制结构主要以转速同步为控制目标,以实现系统输出保持在稳定状态。但在刚性连接结构中,由于齿轮啮合作用,电机转速强制同步,当输出功率达到额定状态,电机转速与转矩成反比,系统外部扰动会作用在转矩输出上[10-12]。

以传统感应电机与啮合齿轮组为研究对象,建立多电机齿轮传动的刚性连接结构系统动力学模型,依据模型分析多电机刚性连接的系统转矩分配不均衡的原因。

如图1所示为啮合齿轮系模型,每台感应电机通过传动轴与小齿轮分别连接,另一端由大齿轮通过输出轴连接负载。齿轮传动模型的扭转运动方程为:

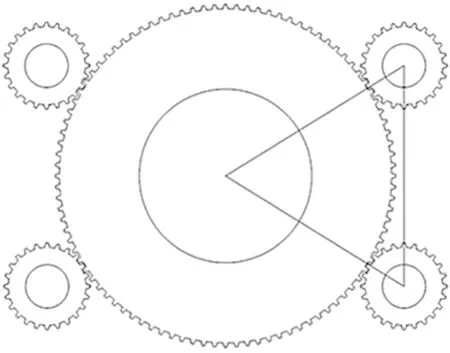
图1 啮合齿轮系示意图

(1)

式中:K和B分别是齿轮的扭转刚度和扭转阻尼,可以通过齿轮半径进行推算,θi为齿轮转动角度,θh为上一级旋转刚体转动角度[13]。将每台电机与该电机连接的齿轮看作整体,将大齿轮与负载看作整体,忽略啮合齿隙,此时,θmi=θpi,θg=θL。则系统动力学方程如下:

(2)

式中:θmi为电机的转子角度,θpi为对应电机的小齿轮旋转角度;θL为负载转子角度,θg为大齿轮的旋转角度;Jmi为电机转动惯量,JL为负载转动惯量;rg为小齿轮半径,Rg为大齿轮半径;Bgi为齿轮阻尼系数,Kgi为齿轮刚度系数;TL为负载转矩,Tei为电机电磁转矩[14]。

假设电机在恒转速下工作,忽略传输功率损耗和齿轮啮合误差,则各电机通过小齿轮传递到大齿轮的驱动转矩以及大齿轮应受转矩为:

(3)

式中,ωi为电机转子角速度,且ω1=ω2=…=ωi;ωR为负载角速度;Pi为电机输出功率;PL为大齿轮应受功率即负载所需功率。由功率平衡原理得PL=P1+P2+…+Pi,大小齿轮的传动比为:

(4)

结合上式得:

(5)

总负载转矩在稳态时近似为恒值,此时,各电机连接的小齿轮输入到大齿轮与负载的驱动转矩近似为负载转矩[15],依据转矩平衡原理:

(6)

由Laplace变换可得时域下的转矩平衡方程:

(7)

由电机运动方程得:

(8)

式中:B为电机摩擦阻力,TLi为负载转矩,Tei为各电机输出电磁转矩,电磁转矩方程为:

Tei=npψistLm/Lr

(9)

式中:np为电机极对数,Lm为励磁自感,Lr为励磁电感。

由式(2)、式(5)可得,从机械运动角度分析,齿轮的摩擦损耗、刚度系数和阻尼系数或是电机转轴磨损都会引起传动结构的转矩输出误差,最终导致各电机负载分配不均衡。机械结构引起的误差会导致电机过载运行,齿轮摩擦损耗加剧,长时间运行下去,就会引发重大事故;由式(8)、式(9)可得,从电机运动角度分析,电机的型号、参数、材料也会影响系统的转矩输出平衡。

现实情况下,这些状况无可避免,仅仅依靠机械结构设计来消除误差,不仅成本高,实行起来也有一定难度。因此,可以借助安全可靠的控制算法来补偿消除这些误差。

2 多电机转矩同步控制

多电机转矩同步控制与转速同步控制原理类似,采用前馈补偿的方式,将各电机的误差补偿到每台电机的转矩外环,系统转矩控制结构图和单台电机的矢量控制原理框图分别如图2和图3所示。

图2 多电机转矩同步控制结构图

图3 单台电机矢量控制原理图

电机的实时转矩信息通过信息接口(一般为变频器或逆变器)传递给上位机,经过控制算法处理,将补偿信号再传递回信息接口,给电机发出动作指令进行相应改变,使系统电机功率趋于平衡状态,从而使转矩趋于平衡。

3 环形耦合控制结构

3.1 转矩补偿控制器

转矩补偿控制器原理结构图如图4所示,其中,KCi为耦合增益系数,Te_ci为补偿转矩。

图4 转矩补偿控制器原理图

根据环形耦合转速控制的转速补偿原理,将其改为转矩控制。转矩环形耦合控制是将某一电机分别与相邻两台电机的转矩内环作为一个整体来处理,电机之间两两做差,再乘以补偿系数,得到电机i的补偿转矩。即:

Te_ci=(Tei-Tei+1)KCi

(10)

式中:Tei为第i台电机电磁转矩,Te_ci为第i台电机补偿转矩。

3.2 补偿系数选取

假设电机参数和控制器模型相同,图5为系统控制结构。

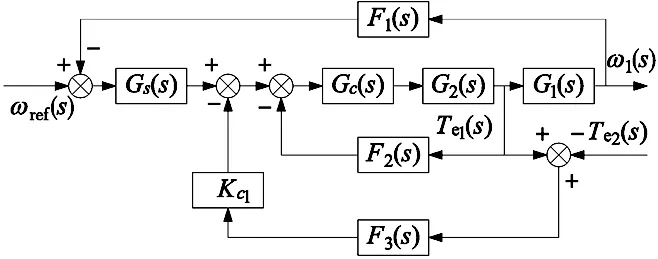
图5 系统矢量程序框图

以电机1为例,GS(s)为转速PI控制器的传递函数,GC(s)为电流PI控制器的传递函数,由PI控制原理可得GS(s)=KP1+1/τ1s,GC(s)=KP2+1/τ2s,其中,Kp1、Kp2为比例增益系数,τ1、τ2为积分时间常数;G1(s)为电机转矩到转速的传递函数,将电机运动方程转到时域内并忽略摩擦阻力,可得G1(s)=1/Jm1s;G2(s)为电机电流到转矩的传递函数,由系统原理图可得,G2(s)≈1;F1(s)、F2(s)、F3(s)为各闭环的反馈传递函数,此处皆设为单位反馈。系统无补偿时的转矩闭环传递函数为:

(11)

此时系统结构可化简为图6所示结构。

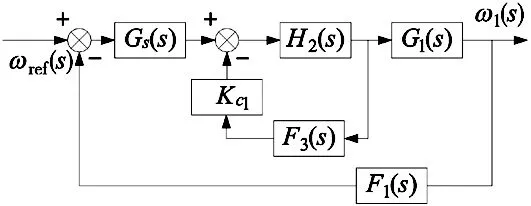
图6 无补偿简化结构图

加入补偿后的转矩内环传递函数为:

(12)

则系统结构可化简为图7。

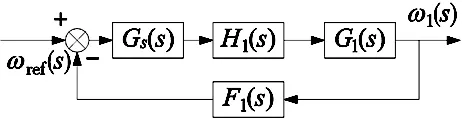
图7 有补偿简化结构图

由梅森公式得系统传递函数为:

(13)

由赫尔维茨判据得系统稳定的充要条件为系统特征方程顺序主子式全部大于0,即Δi>0,则:

(14)

整理得:

(15)

本文所用仿真电机转动惯量为10.18 kg·m2,PI控制器参数经过整定,设置为Kp1=6、τ1=5,Kp2=2、τ2=40,将参数带入式(15)得KC1>-1.5。由此可得,当耦合增益系数KCi满足该条件即可使系统稳定性得到保证。

又因为齿轮传动结构会引起电机输出波动,为了使系统平滑输出,定义Temax(s)、Temin(s)分别为同一时刻系统输出转矩的最大值和最小值,耦合增益系数KCi由各电机的输出转矩共同决定,则本文设计的耦合增益系数可表示为:

(16)

4 仿真结果

在MATLAB/Simulink平台中搭建仿真模型,以传统PI控制策略为对照组,验证所提出控制策略的有效性,依据式(1)～式(9)分别搭建电机组、齿轮组、负载模型以及控制器模型。由于本文研究重点为多电机转矩同步控制,齿轮传动结构只搭建基本模型,不作为变量处理,为便于研究,将齿轮传动比设为1。在对照组和实验组中分别加入扰动信号和突变负载,观察两组电机输出转矩和转矩同步误差的仿真结果。仿真所选用电机和齿轮组的参数如表1和表2所示。

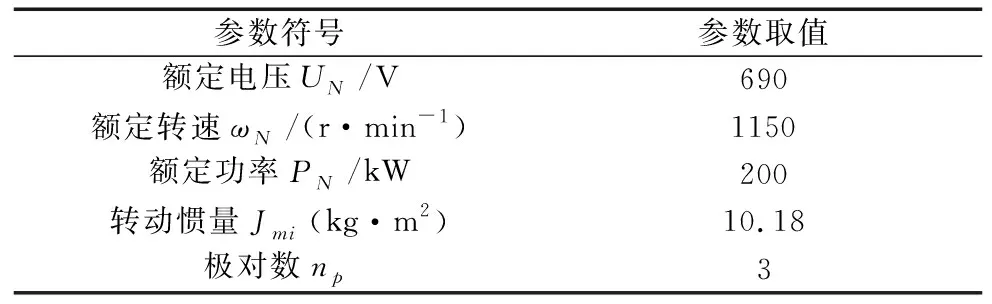
表1 异步电机实验参数

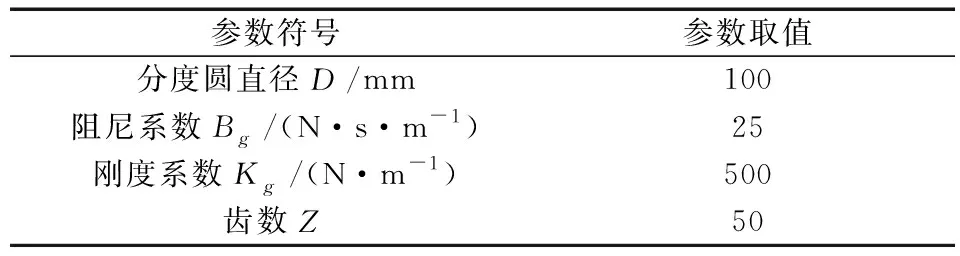
表2 齿轮实验参数

将初始条件设置为4台电机同一给定转速ωref=1150 r/min。由于负载为旋转刚体,所以电机采用变负载启动方式,依据式(7)模拟负载信息,设置负载转动惯量为100 kg·m2。对4台电机的输出转矩进行实时观测,设4台电机间的同步误差:

E(s)=Temax(s)-Temin(s)

(17)

式中:Temax、Temin分别为某时刻4台电机输出转矩中的最大值和最小值,用它们的差值来表征系统同步误差。

4.1 扰动信号仿真

在第10 s给第一台电机施加一个脉冲信号模拟电机组外来扰动,图8～图11分别为PI控制策略下和转矩环形耦合控制策略下4台电机输出转矩和转矩同步误差。

(a) 外部扰动时PI控制下4台电机转矩总体趋势图 (b) 外部扰动时PI控制下4台电机转矩小区域放大图图8 输出转矩图

(a) 外部扰动时环形耦合控制下4台电机转矩总变化趋势图 (b) 外部扰动时环形耦合控制下4台电机转矩小区域放大图图9 输出转矩图

图10 外部扰动时PI控制下4台电机转矩误差 图11 外部扰动时环形耦合控制下4台电机转矩误差

4.2 负载突变仿真

将第一台电机控制参数在2.5%范围内调整,并在第10 s突然施加400 N总负载,图12～图15分别为PI控制策略下和转矩环形耦合控制策略下,第一台电机参数调整,第10 s系统总负载突变后,4台电机转矩和转矩同步误差。

(a) 总负载突变时PI控制下4台电机转矩总变化趋势图 (b) 总负载突变时PI控制下4台电机转矩小区域放大图图12 电机转矩图

(a) 总负载突变时环形耦合控制下4台电机转矩总变化趋势图 (b) 总负载突变时环形耦合控制下4台电机转矩小区域放大图图13 电机转矩图

图14 总负载突变时PI控制下4台电机转矩误差 图15 总负载突变时环形耦合控制下4台电机转矩误差

仿真结果表明,转矩环形耦合控制策略效果明显,系统施加扰动后,对比PI控制策略,转矩误差明显收敛;当系统总负载突变后,对比PI控制策略,系统在0.5 s内迅速恢复到稳定状态,且同步误差也明显缩小,转矩输出波动明显平缓。

5 结论

本文充分分析多电机刚性齿轮传动系统,对传统环形耦合转速控制方法进行改进,成为有效解决多电机齿轮传动过程中转矩不均衡问题的环形耦合转矩控制方法。在系统转矩同步误差收敛的同时,抑制齿轮传动引起的电机转矩输出波动,证明所提出方法的有效性,提高系统的稳定性和可靠性,降低系统内部的机械损耗,延长系统使用寿命。