频率变化条件下负载模拟器改进迭代学习PID控制*
2023-08-02刘晓琳李晋恺
刘晓琳,李晋恺
(中国民航大学电子信息与自动化学院,天津 300300)
0 引言
电动负载模拟器是一种半实物仿真设备,能够在实验室条件下通过加载电机模拟舵机在飞机飞行时所受的空气力矩[1-2],将力矩加载到舵机上来模拟实际工作环境。同时,作为一种绿色环保的测试设备,它可以避免传统全实物实验对舵机的破坏,又能够提高舵机测试实验的可控性与可重复性[3-5]。对于缩短舵机研发周期、节约研发成本有着重要的意义。
舵机测试实验中,舵机是受测对象与承载对象。负载模拟器的加载力矩加载在舵机上,同时舵机自身也在做伺服运动。由于舵机与负载模拟器的加载电机直接相连,舵机与加载电机之间的运动不同步引起的干扰力矩会影响负载模拟器实际输出的力矩值,这种干扰力矩被称为多余力矩。多余力矩会影响实验的准确性,甚至会损坏舵机及负载模拟器。而使用传统PID控制的负载模拟器无法有效地抑制多余力矩。因此,如何抑制多余力矩,从而降低多余力矩引起的输出力矩误差,最终提高输出的模拟力矩精度是负载模拟器研究的关键问题。
针对多余力矩的抑制问题,主要方法有改进PID控制、滑模控制、迭代学习控制等。改进PID控制研究成果众多,主要从改进PID控制器结构与改进调参方法两方面进行,如采用积分先行PID配合神经网络前馈控制[5],采用群智能算法整定参数[6],训练神经网络整定PID参数等[7],但上述方法本质仍是PID控制,控制参数确定后,存在受外部干扰时控制精度下降的缺点。针对PID控制抗扰性差的缺点。代明光等[8]通过扩张状态观测器观测系统综合扰动,基于反步法设计了滑模控制器,通过实验证明该方法能有效抑制多余力矩。但该方法需要系统详细参数进行控制器设计,获取准确参数往往较为困难。迭代学习控制(iterative learning control,ILC)可以通过迭代,自动的调整系统控制量,在不需要系统详细参数的条件下最终实现无差控制。牛国臣等[9]提出了按周期补偿的迭代学习控制器,每经过一个正弦周期便调节预设输入,通过实验证明了该方法在负载模拟器控制问题中的有效性。代明光等[10]针对负载模拟器存在的控制时滞问题,结合PID控制与迭代学习控制,实现了系统的高精度输出。黄静等[11]提出了一种引导信号迭代学习控制,实现了多余力矩的抑制,但由于收敛慢,需要配合其他控制方法才能对输出力矩精准控制。与其他方法相比,迭代学习控制既不需要系统详细参数,也可通过迭代实现控制量的自我调整。这样的特点适合负载模拟器的多余力矩抑制问题。
综上所述,针对负载模拟器存在的多余力矩干扰问题,本文分析了舵机信号频率对多余力矩的影响,提出一种迭代学习PID复合控制器。该控制器通过tanh函数改进的引导信号迭代学习控制器实现系统高精度输出,结合增量式PID控制增加系统抗干扰能力。在固定频率舵机信号与变化频率舵机信号产生的多余力矩影响下均能有效的抑制多余力矩。
1 电动负载模拟器建模与分析
1.1 电动负载模拟器的组成
电动负载模拟器结构示意图如图1所示。按照力矩传递关系,可以分为加载部分与受测舵机部分。加载部分由电机控制器、电机驱动器、加载电机及金属橡胶缓冲弹簧组成。受测舵机部分由受测舵机、力矩传感器及速度传感器组成。系统工作时工控机输出预设力矩信号,经电机控制器、电机驱动器后传递至加载电机,加载电机输出模拟力矩。与此同时,受测舵机在金属-橡胶缓冲弹簧传递的模拟力矩影响下按照实验要求运动,完成测试过程。
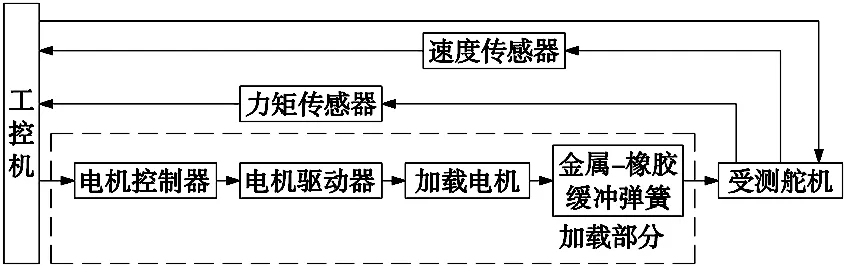
图1 电动负载模拟器简图
实验中受测舵机做位置伺服运动,加载电机输出加载力矩的同时也需要跟随舵机运动。加载部分与受测舵机部分机械机构互相耦合,受测舵机的主动运动产生了影响加载电机输出力矩的多余力矩。因此对多余力矩干扰进行补偿,进而提高加载力矩精度是本文的研究目标。
1.2 电动负载模拟器数学模型
依据图1及系统工作原理建立负载模拟器的数学模型。加载电机是负载模拟器的力矩输出元件。根据加载力矩的特点,选择体积小、转矩大、能长期在堵转状态下稳定运行永磁直流力矩电机。电机电枢回路电压平衡方程为:
(1)
式中:Um为电机电枢电压,im为电机电枢电流,Rm为电机电枢电阻,Lm为电机电枢电感,E为电机反电动势。
在电动机运行过程中,考虑到负载模拟器所受摩擦及外部扰动,电机电磁转矩方程可以表示为:
(2)
式中:Cm为电机转矩常数,Tl为输出力矩,Ff为摩擦力矩,D为外部扰动力矩,Jm为电机转动惯量,Bm为电机阻尼系数,θm为电机轴角位移。
选用PWM(pulse width modulation)驱动器接收电机控制器传输的控制信号,输出驱动电机所需电枢电压。由于驱动器工作频率远大于系统加载频率,在建模时可视为理想比例环节,即表示为:
(3)
式中:uin为负载模拟器控制信号,Um为电机电枢电压,KPWM为驱动器比例放大系数。
理论证明,选择合适的缓冲弹簧可以提高负载模拟器的稳定性,而且在实现变刚度加载的同时,能够降低多余力矩对加载力矩的部分影响[12]。忽略弹簧重量等因素,可以分析得出加载力矩大小与舵机及加载电机之间的转动角度差呈正比例关系。对金属-橡胶缓冲弹簧建模为:
Tl=Kl(θm-θr)
(4)
式中:θm为电机转角,θr为舵机转角,Kl为金属-橡胶缓冲弹簧的弹性系数,Tl为负载模拟器输出力矩。
联立式(1)~式(4),可以建立负载模拟器系统结构如图2所示。
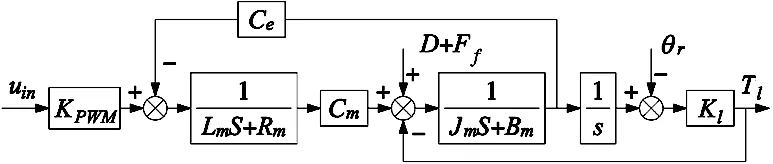
图2 电动负载模拟器系统结构图
1.3 多余力矩分析
根据图2及负载模拟器的数学模型分析可知,舵机工作信号θr是引起多余力矩的主要原因。在过去的研究中,研究者将舵机工作信号设定为固定频率的正弦信号,并未考虑过频率变化的情况[12-15]。但是实际中多余力矩的干扰是两方面的,一方面多余力矩干扰加载电机,使它输出的实际力矩与预设模拟力矩产生误差。同时,干扰力矩也会干扰舵机,让做伺服运动的舵机无法按照预设信号运动。因此,研究复杂舵机动作信号引起的多余力矩是实际存在的问题,并且是十分必要的。为了研究舵机工作信号频率对多余力矩的影响,根据系统数学模型在MATLAB中建立负载模拟器仿真系统。系统中参数如表1所示。设定模拟力矩预设信号uin为幅值为50 N·m,频率是1 Hz的正弦信号。舵机工作信号θr幅值为5 N·m的正弦信号,第一组实验中θr信号频率为1 Hz不改变,另一组实验θr频率从1~10 Hz均匀变化。两组实验均采用传统PID控制方法。此时系统预设模拟力矩与实际输出力矩如图3和图4所示。

表1 仿真系统参数
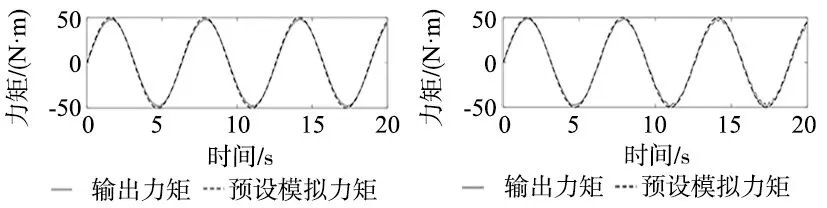
图3 舵机信号频率固定时输出力矩图 图4 舵机信号频率变化时输出力矩图
由图3和图4分析可知,当舵机信号频率固定时,系统输出力矩波形与预设力矩基本一致。但由于多余力矩的干扰,即使采用了PID控制的负载模拟器输出力矩与预设力矩仍存在明显误差。当舵机信号频率变化时,随着频率变化,输出力矩和预设力矩间的误差发生了明显变化。这表明面对变化频率的舵机信号引起的多余力矩更加复杂,固定参数的PID控制器已经无法满足控制要求,需要设计能够在运行中自调节控制量的复合控制器解决负载模拟器控制问题。
2 电动负载模拟器控制器设计
在数学建模的基础上与多余力矩分析的基础上,针对负载模拟器的多余力矩抑制问题,本文提出了结合PID控制与迭代学习控制的复合控制器如图5所示。
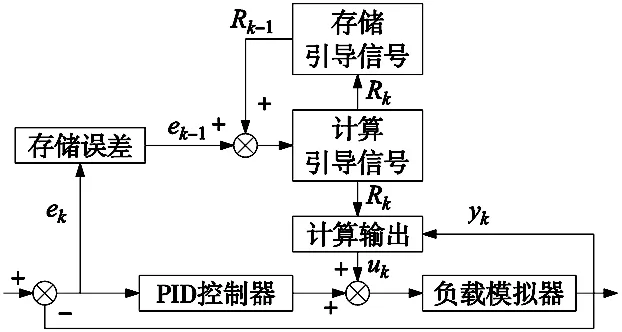
图5 复合控制器结构图
该复合控制器有如下两点创新之处:
(1)提出了符号函数积分改进的引导信号迭代学习控制。首先,通过引导信号机制进行迭代学习,既可以在迭代中对误差进行限制,防止系统误差过大引起系统失控,又不要迭代学习严格的初态相同的条件;其次,通过符号函数积分加速迭代学习控制收敛速度,并证明改进后的控制方法的收敛条件。
(2)结合PID控制与改进迭代学习控制组成复合控制器。迭代学习控制可以通过迭代不断的降低跟踪误差,PID控制增加了复合控制器的抗扰性,并且为迭代学习控制提供初始的控制量加速迭代过程。
tanh函数积分改进的引导信号迭代学习。迭代学习控制是根据系统的跟踪误差,通过迭代对控制量进行调整,进而不断提高控制精度的一种控制方法,被广泛应用于控制领域。其控制律如下:
(5)
式中:k为第k次迭代,yd为系统预设输入,yk、ek、uk分别为系统在第k次迭代时的输出、跟踪误差及第k次迭代时的输入。但是因为系统中存在时滞及输入输出间相位延迟,传统迭代学习控制会在负载模拟器运行中出现失控问题。为此,黄静等[11]提出了一种ILC可以表示为:
(6)
式中:l(k)为第k次迭代时的引导信号,ε为系统学习参数。
该方法结合了迭代学习控制与PID控制两种控制方法的优点。既引入了引导信号代替误差对控制量进行调整。通过引导信号机制可以保证迭代中不会出现失控问题。但是引导信号机制降低了系统误差收敛的速度。误差收敛慢。
针对该问题,本文引入了符号函数积分对引导信号迭代学习进行了改进,改进后的控制律为:
(7)
式中:p、h为常数,调节引导信号的迭代速度。tanh函数,具体为:
(8)
tanh函数的误差积分在迭代中的作用类似于PID控制中的积分作用。与单纯的积分相比。tanh函数项的积分项在受到干扰时由于该函数具有有界性,能够防止下一次迭代时控制量变化过大,提升了迭代学习控制的抗扰性。与新型的符号积分改进相比,tanh函数可以在误差较小时精确的对下一次迭代中的控制量调整,而在小误差时消除符号积分引起的控制量抖动问题。这种改进既能够加速迭代过程,这使得改进后的迭代学习控制精度更高,收敛更快。
对于本文提出的迭代学习控制的收敛条件证明为:
对存在n个状态变量的系统:
(9)
式中:k=1,2,3为迭代次数,A、B、C为系统系数矩阵,xk(t)、yk(t)、uk(t)分别为系统在第k次迭代时的状态向量、输出向量、输入向量。其具体表达式分别为:
xk(t)=[xk1(t),xk2(t),xk3(t),…,xkn(t)]T
(10)
yk(t)=[yk(1),yk(2),yk(3),…,yk(n)]T
(11)
uk(t)=[uk(0),uk(1),uk(2),…,uk(n-1)]T
(12)
系统第k次的输出为:
yk=CAn-1Buk(0)+CAn-2Buk(1)+…+
CBuk(N-1)+CANxk(0)
(13)
该式简化为:
yk=Guk+Dxk(0)
(14)

系统在k+1次迭代后的误差ek+1为:
ek+1=yd-yk+1=yd-Guk+1-Dxk+1(0)=
yd-G[p(rk+1-yk+1)+
h(tk+tanh(ek))]-Dxk+1(0)
(15)
根据式(7)和式(15)可得:
ek+1=yd-G[p(rk-yk)+h(tk-1+tanh(ek-1))+
p(Lek+yk-yk-1)+h(tk+tanh(ek))-
h(tk-1+tanh(ek-1))]-Dxk+1(0)=
yd-Guk-Dxk(0)-pG(Lek+yk-yk-1)-
Gh(tanh(ek-1))+Dxk(0)-Dxk+1(0)
(16)
由于负载模拟器引导信号与输入输出信号具有周期性,即当rk(t)=rk-1(t)时可得:
(17)
同时,对于迭代学习时间上的连续性,有xk+1(0)=xk(N),及系统初始状态的一致性xk+1(0)=xk(0)。结合式(9)可得:
xk+1(0)=Anxk(0)+Quk
(18)
式中:Q=[AN-1B,AN-2B,…,AB,B]。
根据式(18)可得:
xk+1(0)-xk(0)=Qpek+Qp(l-1)ek-1+Qh(tanh(ek-1))
(19)
联立式(19)和式(16)可以得到:
(I+GP)ek+1=ek(I-GPL+GP-DP)+ek-1(-pL+p)-
Ghtanh(ek)-DQhtanh(ek-1)
(20)
矩阵I+GP可逆,两边同时乘I+GP的逆可得:
ek+1=(I+GP)-1[ek(I-GPL+GP-DP)+
ek-1(-pL+p)-Ghtanh(ek)-DQhtanh(ek-1)]
(21)
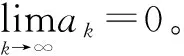
对式(21)两边同时取范数,根据不等式进行缩放可以得到:
(22)
即只要满足:
(I+GP)-1[(GPL+GP-DP)+(-pL+p-I)]<1
此时本文提出的改进引导信号迭代学习控制便是收敛的。
3 电动负载模拟器多余力矩抑制实验
基于负载模拟器数学模型在MATLAB中建立仿真系统,其中各参数如表1所示。实验分为两组,第一组实验在固定频率舵机信号引起的多余力矩下,验证本文所提复合控制器对多余力矩的抑制效果。第二组实验在变化频率舵机信号引起的多余力矩下,验证本文所提复合控制器对更复杂多余力矩的抑制效果。
3.1 固定频率舵机信号多余力矩抑制实验
在舵机工作信号为固定频率5 Hz的条件下,设定模拟力矩预设信号为幅值是50 N·m的正弦信号,工作频率分别为1 Hz和4 Hz。20次迭代后力矩加载实验结果如图6所示,输出力矩与预设力矩误差如表2所示。每一次迭代的误差示意图如图7所示。

(a) 预设力矩频率为1 Hz,20次迭代后输出力矩曲线 (b) 预设力矩频率为4 Hz,20次迭代后输出力矩曲线图6 输出力矩曲线
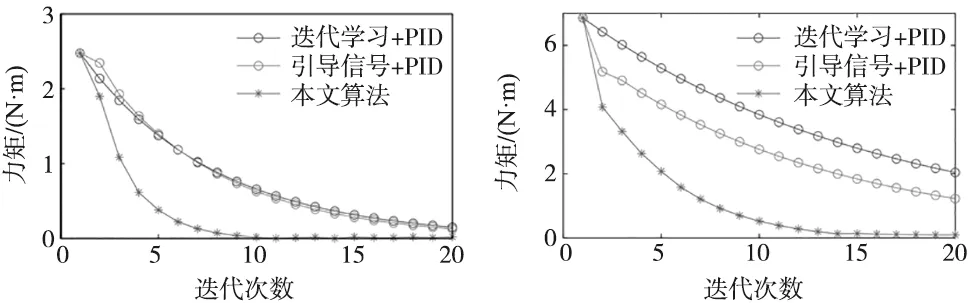
(a) 预设力矩频率为1 Hz时迭代误差曲线 (b) 预设力矩频率为4 Hz时迭代误差曲线图7 迭代误差曲线

表2 20次迭代后系统输出力矩与预设力矩误差
由图6分析可知,20次迭代后,3种控制方法的输出力矩均能随预设模拟力矩,但迭代学习PID控制与引导信号与迭代学习PID控制的误差相比本文算法更大。结合表2分析可知当预设模拟力矩频率为1 Hz时,迭代学习PID控制与引导信号PID在20次迭代后力矩误差分别为0.151 N·m和0.129 N·m。而本文提出复合控制器力矩误差为0.011 N·m。相比之下误差降低了92.7%和91.5%。当模拟力矩频率为4 Hz时,本文方法的力矩误差相比迭代学习PID控制器与引导信号PID控制器下降了92.7%和95.8%。这表明本文提出的tanh函数改进的引导信号迭代学习PID控制器能对负载模拟器多余力矩进行抑制,使输出力矩精度更高。
由图7及表2分析可知,随着迭代次数增加,3种控制方法的跟踪误差均在下降。最终迭代20次后本文算法的输出力矩误差最低。并且在第一次迭代后每一次迭代本文算法的误差均低于其他两种控制器。这表明本文提出的复合控制器收敛速度更快,能够更快的实现模拟力矩的高精度输出。
3.2 非周期性多余力矩抑制实验
设定模拟力矩预设信号为幅值是50 N·m的正弦信号,工作频率分别为1 Hz和4 Hz。在舵机工作信号频率从0.1 Hz到5 Hz变化的条件下进行力矩加载实验,此时多余力矩更为复杂,实验结果如图8、图9和表3所示。
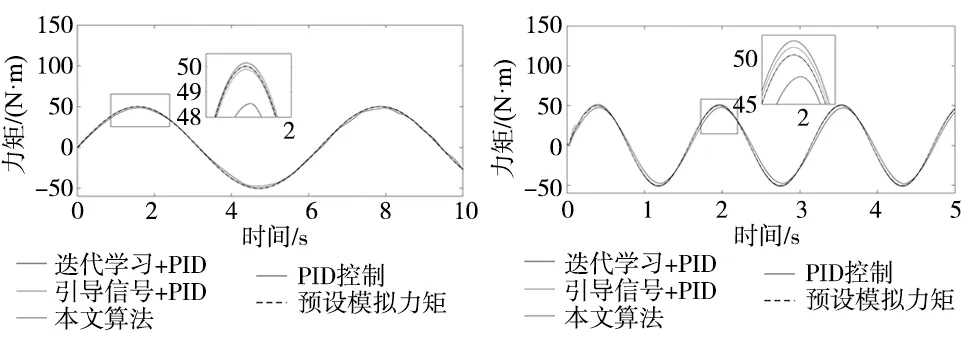
(a) 预设力矩频率为1 Hz,20次迭代后输出力矩曲线 (b) 预设力矩频率为4 Hz,20次迭代后输出力矩曲线图8 输出力矩曲线
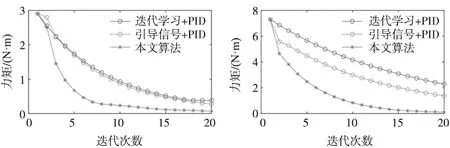
(a) 预设力矩频率为1 Hz时迭代误差曲线 (b) 预设力矩频率为4 Hz时迭代误差曲线图9 迭代误差曲线

表3 20次迭代后系统输出力矩与预设力矩误差
对比图6和图8分析可知,当舵机信号频率变化后,引起的多余力矩变化导致输出力矩的跟踪误差随之增加。4种控制方法中PID控制误差最大,甚至图6a中输出力矩波形不是平滑的正弦曲线,而使用迭代学习控制的其他3组都误差更小,输出力矩波形与预设力矩基本一致。
由图8及表3分析可知。当预设模拟力矩频率为1 Hz时,迭代学习PID控制与引导信号PID控制在20次迭代后误差分别为0.381 N·m和0.272 N·m。而本文提出复合控制器跟踪误差为0.069 N·m。相比之下误差降低了81.9%和74.6%。当预设模拟力矩频率为4 Hz时,本文方法的跟踪误差相比迭代学习PID控制器与引导信号PID控制器下降了95.1%和92.0%。这表明本文提出的复合控制器能抑制由变频率舵机信号引起的更复杂的多余力矩。
由图7a和图9a对比可知,在预设力矩信号相同时,变化频率舵机信号引起的多余力矩造成的力矩误差大于固定频率舵机信号的力矩误差。由图9分析可知,第一次迭代以后,面对更复杂的多余力矩,迭代学习控制能够通过迭代降低跟踪误差。本文提出的复合控制器在每次迭代时跟踪误差都低于其他两种迭代学习复合控制器。
4 结论
本文针对电动负载模拟器多余力矩干扰严重的问题,提出了一种可行的控制优化方案。
首先,依据系统机构组成与工作原理,构建了系统的数学模型。基于数学模型与仿真实验分析了舵机工作信号频率变化对多余力矩与输出力矩跟踪误差的影响问题。然后,针对变化频率舵机工作信号引起的复杂多余力矩问题,提出了基于tanh函数的改进型引导信号迭代学习控制和增量式PID控制的复合控制策略。并给出改进算法的收敛条件。该复合控制器结合了PID控制与引导信号迭代学习控制的优点。既能加速迭代,提高抗扰性。同时能自动调整控制量,从而实现对由固定频率舵机工作信号频率和变化频率舵机工作信号引起的多余力矩多余力矩的抑制。
最后采用MATLAB仿真实验验证了:本文提出的复合控制器能够抑制由固定频率舵机工作信号频率和变化频率舵机工作信号引起的多余力矩。改进后的复合控制器与传统迭代学习PID控制相比,由于引导信号机制对迭代学习的加速效果及tanh函数改进对控制精度的提高效果,在相同迭代次数下复合控制器的跟踪误差更低,收敛速度更快,性能优于传统迭代学习PID控制器,能够满足电动负载模拟器输出力矩控制的精度要求。
综合考虑本文内容和领域的发展,在后续研究中可以考虑舵机信号频率的变化形式对多余力矩的影响。以及舵机信号为正弦信号以外的信号如方波、三角波时,多余力矩的表现形式及控制方法对多余力矩的控制效果。
