永磁同步电机改进非线性反步自抗扰位置控制*

何栋炜,林杭彬,刘丽桑,陈 健,曾志伟,王 佩

(福建工程学院 a.电子电气与物理学院;b.福建省工业集成自动化行业技术开发基地;c.电子信息与电气技术国家级实验教学示范中心,福州 350118)

0 引言

近年来,永磁同步电机(permanent magnet synchronous motor,PMSM)位置伺服系统被广泛应用于工业机器人、航空航天及数控机床等领域中。而PMSM是一个具有多变量、非线性和强耦合的复杂控制对象,其位置跟踪性能易受负载转矩扰动及电机参数摄动等因素影响,传统的PID算法难以实现高精度的控制。随着控制理论的发展,近些年,多种控制方法被引入PMSM位置伺服系统中,如滑模变结构控制[1-2]、智能控制[3-4]、自适应控制[5-6]等,这些控制策略在位置伺服系统中取得了一定的成效。

韩京清[7]在PID控制基础上提出自抗扰控制(active disturbance rejection control,ADRC)。ADRC将系统的内部扰动、外部扰动及所有不确定因素归结为总和扰动,通过扩张状态观测器(extended state observer,ESO)对总和扰动及各状态变量进行实时观测,并采用非线性状态误差反馈律(nonlinear state error feedback,NLSEF)对各状态的误差进行反馈调节,最终对扰动进行补偿。ADRC不依赖于精确的数学模型、无超调,具有一定的抗干扰能力,因此也被应用于永磁同步电机位置伺服系统中,并得到了不断改进。刘春强等[8]提出了位置-电流双环自抗扰控制,设计了位置环二阶ADRC和电流环一阶ADRC,提高了系统抗负载转矩扰动能力。左月飞等[9]受滑模控制的一体化设计启发,提出了位置-转速一体化的设计方法,实现四段式位置伺服系统控制,解决了传统二阶ADRC中转速不可控的问题。刘丙友等[10]对ESO和NLSEF进行改进,设计了一个在原点附近具有较好平滑性的非线性函数代替传统非线性函数,使系统具有较好的抗干扰能力和鲁棒性。HUANG等[11]结合了分数阶PID理论,提出了分数阶ESO,改善了系统的抗干扰性能。周新力等[12]将ADRC与反步法相结合,并在反步法中加入了积分项以确保位置角跟踪误差能够趋于0,提高位置跟踪精度。

但是在传统ADRC中,NLSEF设计要求已知系统实际控制增益(转矩系数与转动惯量的比值称之为控制增益),才可使得系统具有理想的控制性能[13]。然而永磁同步电机位置伺服系统的控制增益存在不确定性,转矩系数或转动惯量会随着运行状态发生变化,显然会导致使用控制增益的理论值设计得到的ESO的观测精度下降,从而影响控制器对扰动的补偿效果,影响系统的抗干扰性能。针对上述问题,本文设计一种改进的非线性反步自抗扰控制方法。首先,在NLSEF设计过程中引入反步设计方法,并优化设计实现未知控制增益下NLSEF的设计,此外,引入连续光滑的非线性函数,进一步改善控制器的收敛性能。其次,考虑永磁同步电机位置伺服系统的模型结构,引入朗道自适应观测器代替ESO,对系统参数及扰动进行辨识与补偿,提高控制器的控制精度。

1 PMSM位置伺服系统数学模型

在忽略铁心饱和、不计涡流损耗和磁滞损耗等情况下,采用id=0矢量控制,PMSM位置伺服系统动态数学模型可以表示为[14]:

(1)

式中:kT为转矩系数,θ为转子位置角,ωm为转子机械角速度,iq为定子电流q轴分量,J为转动惯量,B为粘滞系数,TL为负载转矩。

2 非线性反步自抗扰位置控制

针对参数不确定性及外部扰动对永磁同步电机位置伺服系统的跟踪性能的影响,本文设计了一种改进的非线性反步自抗扰控制方法,该控制方法由跟踪微分器(tracking differentiator,TD)、非线性反步控制器和朗道自适应观测器3个部分组成,基于本文所提出的改进非线性反步自抗扰控制方法的PMSM位置伺服系统结构如图1所示。

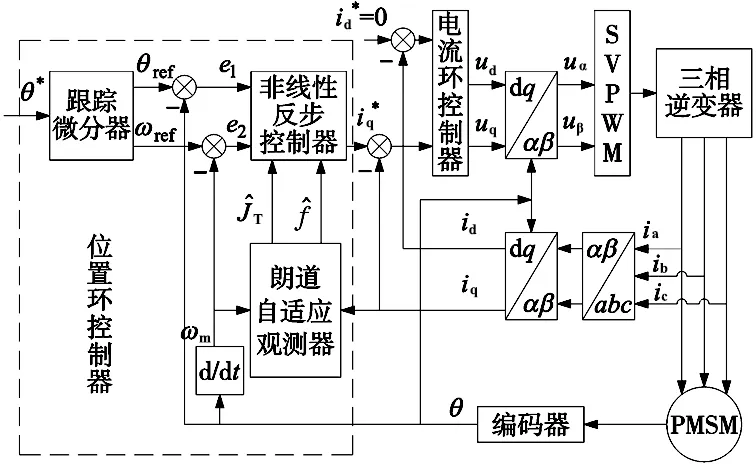
图1 PMSM位置伺服系统结构图

2.1 跟踪微分器

给定位置轨迹往往会存在突变,导致误差瞬间过大,对控制器造成冲击。因此在控制器结构中,引入跟踪微分器为给定位置轨迹安排过渡过程,同时为后端控制器提供位置和转速的给定轨迹,其表达式为[15]:

(2)

式中:θ*为跟踪微分器的输入信号,θref、ωref分别为跟踪微分器生成的转子位置和转速的给定值,r为速度因子,h0为滤波因子,fhan(θref-θ*,ωref,r,h0)为最速控制综合函数,其表达式为:

(3)

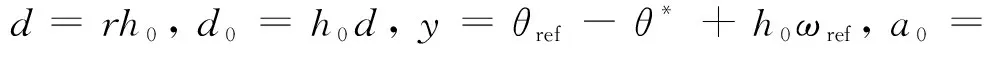
(4)

在跟踪微分器中,r的取值决定了系统的响应速度,取值越大则系统响应速度越快,过渡过程时间越短。若r的取值过大,将导致给定位置响应速度过大,使系统产生超调,因此需根据系统的承受能力来决定r的取值[16]。h0决定了滤波效果,适当选取该参数可有效抑制输入信号的噪声,该参数的取值与采样周期有关。当h0的取值与采样周期相同时,只需通过调节r来改变过渡过程的速度,同样可抑制噪声。

2.2 非线性反步控制器设计

反步法易于与自抗扰控制结合从而得到了广泛的应用。而传统反步控制器在设计过程中,对于每一阶子系统中待设计部分采用线性方式进行设计,使得最终设计出的控制律只能通过改变增益系数调节控制器的收敛速度及扰动抑制能力。为获得较好的抗干扰性能,往往需要较大的增益系数。但大增益易使控制器饱和,甚至使系统振荡。再之,系统转矩系数与转动惯量的变化使得控制增益发生改变,致使控制器无法精确地补偿扰动,影响了控制器的控制精度。积分反步控制器虽然在待设计部分加入了积分项使误差逼近于0,但仍存在上述问题。为解决传统ADRC必须已知控制增益及收敛性能有待改善的问题,本文提出了一种非线性反步控制器,通过模型变换优化控制器设计,并在控制器设计过程中引入具有“大误差,小增益;小误差,大增益”特性的连续光滑非线性函数使得所设计的控制器具有更好的收敛性能及更强的扰动抑制能力。

记JT=J/kT,BT=B/kT,TT=T/kT,则式(1)可改写为:

(5)

记转子位置角θ为状态变量x1,转子机械角速度ωm为状态变量x2,f=BTωm+TT为总和扰动,u=iq为控制量,可得系统的状态方程为:

(6)

首先,建立系统误差方程为:

(7)

由式(5)和式(7)可得:

JTe2=JT(ωref-ωm-φ)

(8)

进一步,将式(8)两边对时间求导,并将式(6)代入可得:

(9)

取Lyapunov函数为:

(10)

则式(10)沿系统的导数为:

(11)

取:

(12)

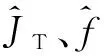
由式(12)得非线性反步控制律为:

(13)

(14)

式(11)可以改写为:

(15)

由于e2及ρ均有界,进一步可得:

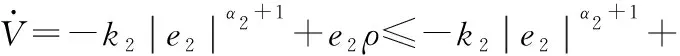
(16)

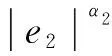
(17)

由式(17)可知,通过调节参数k2与α2的值可改变e2的收敛域。显然,当k2越大、α2越小时,e2将收敛至更小的范围内。

此外,为改善抖振问题,采用连续光滑的非线性函数qin(x,α,δ)代替sigα(·)函数[18],qin(x,α,δ)函数表达式如下[19]:

(18)

式中:q1=δα-1,q2=-(α-1)δα-2,q3=(α-1)δα-3,δ为线性区间,α为幂次,用于改变函数非线性程度。

2.3 朗道自适应观测器

根据上节分析,系统跟踪误差取决于ρ,因此提高对系统不确定参数JT、f的估计精度才能根本上提高系统的跟踪性能。朗道离散时间递推算法属于模型参考自适应算法。该算法以实际模型作为参考模型,并建立含待辨识参数的未知参数的可调模型,将参考模型与可调模型的误差通过自适应律调节可调模型的参数,使得可调模型可以无限逼近参考模型,最终根据递推机制得出待辨识参数[20-22]。系统不确定参数的朗道自适应观测器设计如下。

由式(5),系统可以表示为:

(19)

对式(19)进行离散化处理后得:

(20)

式中:Ts为采样周期。

根据式(20)可以建立系统参考模型为:

y(k)=φT(k-1)θ

(21)

式中:y(k)=ωm(k)-ωm(k-1),θT=[λζ]为待辨识参数向量,φT(k-1)=[iq(k-1) 1]为系统输出向量,λ=Ts/JT,ζ=-Tsf(k-1)/JT。则可调系统的先验输出为:

(22)

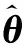
先验广义误差为:

(23)

对于并联可调系统,采用自适应律[23]:

(24)

式中:K(k)为自适应增益向量,其表达式为:

(25)

式中:I为单位矩阵,P(k)为误差的协方差矩阵;μ为遗忘因子,表达式为:

(26)

式中:0<μ1≤1,0<μ2<2,μ1、μ2为遗忘因子的权重。根据系统的特点,适当地选取μ1和μ2的取值,可调节自适应律收敛性能。

根据递推机制得到JT和f的估计值为:

(27)

综上所述,采用朗道算法可实现同时对JT和f进行辨识,在递推过程中只与q轴电流和转速误差有关,独立性较高。此外,通过选取适当的遗忘因子权重,可减小由负载变化对辨识结果的影响,提高算法的辨识精度,算法收敛性分析详见文献[24]。朗道自适应观测器结构图如图2所示。

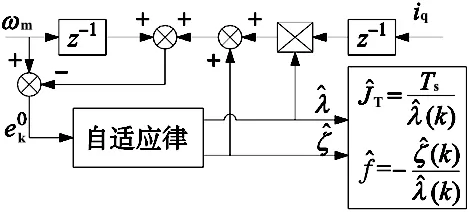
图2 朗道自适应观测器结构图

3 仿真分析

为验证本文所提出的非线性反步自抗扰控制方法的有效性,本文使用Simulink对本文所提出方法进行仿真测试,并与文献[12]的积分反步自抗扰控制方法进行对比。仿真中使用的永磁同步电机参数如表1所示。电流环采用内模控制[25],控制器采样周期Ts=100 μs。

文献[12]中积分反步控制器形式为:

(28)

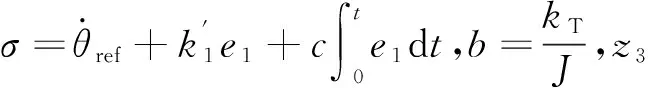
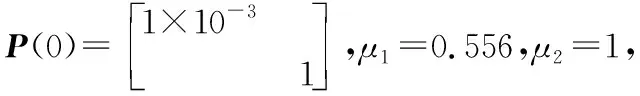
3.1 阶跃响应测试

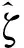
图3～图5分别给出了两种控制方法的位置跟踪轨迹、位置跟踪误差及q轴给定电流。从图3的跟踪结果可以看出,在0～0.2 s电机空载运行时,两种方法跟踪阶跃信号时无超调,均能较好跟踪阶跃给定。由图4的位置跟踪误差可知,积分反步自抗扰方法的响应时间为42 ms(误差±0.1%内),而非线性反步自抗扰方法的响应时间为20 ms。在跟踪过程中0.2 s时突加负载转矩,积分反步自抗扰方法的位置跟踪曲线在负载突变时存在0.14 rad的波动,经40 ms误差收敛至0 rad;而本文所提出的非线性反步自抗扰方法在突加负载时其位置轨迹仅存在0.007 5 rad的暂态误差,经8 ms误差收敛至0 rad。图5给出了阶跃响应测试过程中q轴给定电流曲线,在稳态时,二者给定电流基本相同。当突加负载时,从给定电流曲线可以看出本文方法控制律响应快,收敛速度快,抗扰动性能要优于积分反步自抗扰方法。

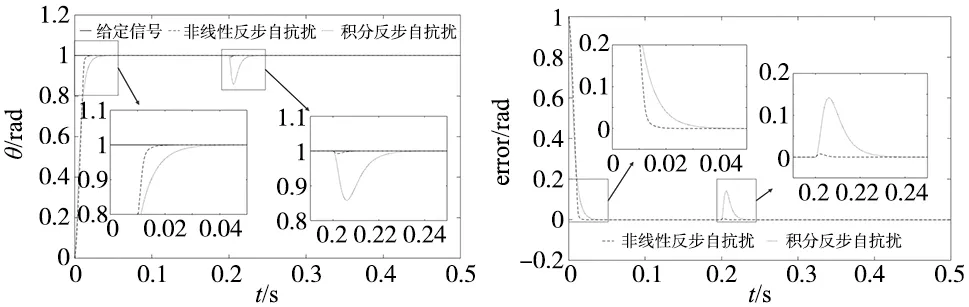
图3 阶跃响应测试结果 图4 阶跃响应测试下位置跟踪误差

测试对比数据如表2所示,相比于积分反步自抗扰方法,本文所提出的方法具有更快的响应速度及抗扰动能力。

表2 阶跃响应测试结果对比

(a) JT辨识结果 (b) f辨识结果图6 阶跃响应测试下辨识结果

(a) JT辨识放大图 (b) f辨识放大图图7 阶跃响应测试下辨识结果放大(0～0.015 s)

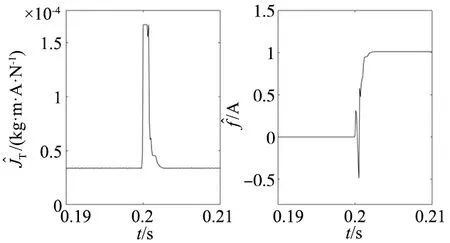
(a) JT辨识放大图 (b) f辨识放大图图8 阶跃响应测试下辨识结果放大(0.19～0.21 s)

3.2 正弦跟踪测试

正弦跟踪测试结果如图9～图12所示。从图9中跟踪结果来看,两种方法同样可以较好地跟踪正弦给定轨迹。进一步由图10和图11中可以看出,电机空载运行时(0～0.2 s),两种方法在电机运行初期均产生较大的误差,但本文方法在初期误差较大时可快速收敛。进入稳态时,采用积分反步自抗扰方法的位置跟踪误差波动范围为±0.011 5 rad,而本文方法的位置跟踪误差波动范围为±0.009 8 rad。在0.2 s时突加负载转矩后,采用积分反步自抗扰方法时位置跟踪误差最大值为0.145 rad,恢复时间约35 ms。本文方法将最大跟踪误差控制在0.039 rad,恢复时间约15 ms。由图12可以看出,相比积分反步自抗扰方法,本文方法的控制响应快,收敛速度与位置跟踪结果一致。测试对比数据如表3所示。通过对比可以看出,在电机运行初期误差较大和突加扰动时,本文方法的控制律大于积分反步自抗扰方法(见图12),调节速度快,对扰动的抑制效果更佳。

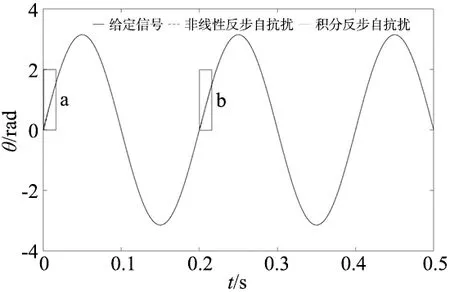
图9 正弦跟踪测试结果

(a) 正弦跟踪放大(0～0.15 s) (b) 正弦跟踪放大(0.2～0.215 s)图10 正弦跟踪测试结果放大图

图11 正弦跟踪误差 图12 正弦跟踪测试下给定电流

表3 正弦跟踪性能对比

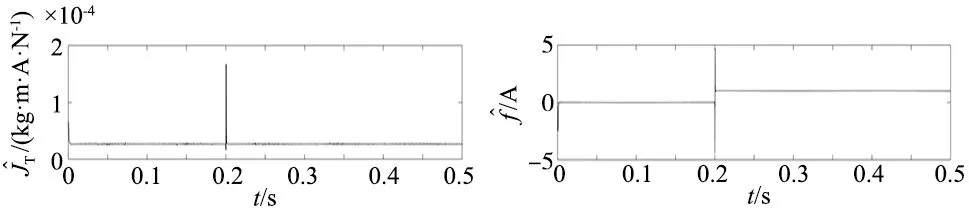
(a) JT辨识结果 (b) f辨识结果图13 正弦响应测试下辨识结果

(a) JT辨识放大图 (b) f辨识放大图图14 正弦响应测试下辨识结果放大(0～0.004 s)

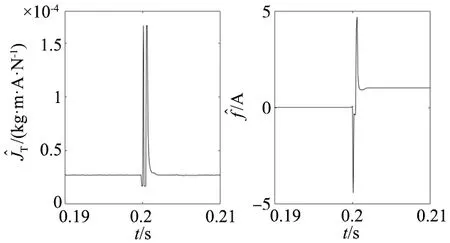
(a) JT辨识放大图 (b) f辨识放大图图15 正弦响应测试下辨识结果放大(0.19～0.21 s)

上述仿真结果表明,当系统存在扰动和参数失配时,本文所提出的非线性反步自抗扰控制方法收敛速度快、扰动抑制强,具有更好的抗干扰能力。

4 结论

针对扰动及参数失配影响PMSM位置伺服系统轨迹跟踪性能的问题及传统自抗扰控制器的不足,本文提出了一种改进的非线性反步自抗扰控制方法。在传统自抗扰控制器的基础上,采用反步设计法,并引入连续光滑的非线性函数设计了非线性控制器,解决了传统自抗扰控制器需要已知控制增益的问题,并进一步改善控制器的收敛性能;采用带遗忘因子的朗道算法对系统参数及扰动进行精确辨识,提升控制器的补偿控制精度。仿真结果表明,相比于积分反步自抗扰控制,本文所提出的方法具有更快的收敛速度以及更强的抗干扰能力,可以有效地提高PMSM位置伺服系统的轨迹跟踪控制性能。