基于半边折叠代价算法的数字孪生模型构建*
2023-08-02刘小奇王雅君王德权冷峻宇
刘小奇,王雅君,王德权,冷峻宇
(大连工业大学机械工程与自动化学院,大连 116034)
0 引言
随着中国制造2025等战略的不断推进,数字孪生已经成为实现传统制造业向数字化、智能化转型升级的重要途径,各制造企业都在积极研究与实现数字孪生在真实生产中的落地应用。美国是最早开展数字孪生研究与应用的国家,主要将数字孪生应用于航空航天的健康监测、运行维护、寿命预测等方面,近些年在智能工厂、智慧城市、3D打印等方面开展了应用探索;在德国以西门子、亚琛工业大学为代表的工业4.0主推和实施机构,开展了大量数字孪生研究与实践;国内方面,对数字孪生的研究起步较晚 ,但最近几年专家学者对此部分研究越来越重视,使得数字孪生在理论研究和应用技术方面取得了快速进步,陶飞等[1-2]对数字孪生在制造领域的应用实践中出现的问题与难点进行研究,提出了数字孪生车间的概念及构建方法,并针对如何构建数字孪生模型问题,探索建立了一套数字孪生模型构建理论体系,就数字孪生助力装备数智化升级,提出了数字孪生装备三阶段发展路径及关键技术。杜莹莹等[3]就数字孪生对工业机器人监控进行研究。
而目前国内的多数企业加工生产线中的孪生模型都存在建模时精细化不足,模型过大的问题,模型无关顶点的数量较多,内部结构过于复杂,造成在模型仿真页面同步物理实体显示时出现缓慢卡顿等现象,无法实时呈现物理实体的状态[4],所以提出在构建数字孪生模型时依据模型构建的基本准则,进行模型的网格化及轻量化处理。根据真实生产过程中的反馈,使数字孪生模型具备精确化、可视化、轻量化、易交互、易进化特性[2]。
1 数字孪生模型构建
1.1 模型数据采集
本文使用blender进行建模,blender提供了强大的基于特征的实体建模功能。
为保证数字孪生模型的精确化,也就是保证数字孪生模型在生产过程中显示和产生的数据的可信、可用和准确,对物理设备进行拆分,对其最小单元进行数字孪生建模,建模完成后对所有单元进行组装,形成数字孪生模型整体。
首先对物理设备进行360°扫描,获得模型整体数据,包括三维坐标数据、曲率数据等,在单元组装时严格按照此部分数据进行;再对拆分后的最小单元零件进行扫描,获得小单元零件数据,包括零件形态、尺寸等数据,并将此部分数据进行等比例缩小,用于模型组件的建模,使数字孪生模型为物理设备的等比例缩小件,保证模型精确化的要求。
1.2 模型组件构建及组装
模型的可重构特性是指,在不同的生产环境中,模型能够灵活调整自身结构和参数配置,可进化特性是指模型能够根据物理设备和应用环境变化,对模型功能进行持续性的优化[3]。而对模型最小单元建模再进行组装恰好能够满足以上两点要求,当模型需要重构时只需对模型最小单元按要求从新组装即可,当模型需要简化时,只对需要改变的单元进行操作,其他单元保留,可减少模型简化时的操作。
在blender软件中建模,首先进行草图的绘制,选择基准平面,绘制此平面上模型的草图,在根据扫描所得零件数据对草图进行拉伸,而且blender智能尺寸等功能,可以对模型的尺寸等参数进行实时的修改,保证了模型的精确性。
对模型单元零件构建完成后,则需对其组装,生成完整孪生模型。首先要确定零件模型的层级关系,来保证正确的组装顺序;其次确定模型组装过程中的空间约束条件,即扫描所得的模型整体数据,包括三维坐标数据等,来保证模型最终安装的准确性,最后根据组装顺序和约束条件实现模型的组装。
2 基于半边折叠算法的模型简化
在真实数字孪生车间运行时,数字孪生车间要求现实物理设备与孪生模型在时空上高度一致[4],但是模型过多的顶点和内部复杂结构,对模型运行环境要求很高,都会导致数字孪生车间和物理车间两者间数据传输速度和模型显示时的卡顿。
为了满足模型的轻量化要求,即使用精简的模型来将现实设备的几何特征充分表现,所以对构建的数字孪生模型进行轻量化处理。
2.1 模型轻量化流程
对构建完成的数字孪生模型表面选择大量的采样点,构造出模型的三角网格模型,然后采取半边折叠算法,选取折叠代价小的边进行折叠,目的是将模型几何特征不突出部分的三角形进行合并,用较少数目的三角形网格表示更多的信息,使得数字孪生模型达到轻量化要求,且模型的重要特征不丢失[5]。图1为半边折叠算法流程。

图1 半边折叠算法流程图
对构建完成的数字孪生模型生成三角网格模型,计算所有折叠边的折叠代价,并根据折叠代价生成从小到大的有序队列。计算步骤为:
步骤1:取出队首元素,判断其折叠代价是否小于模型简化要求阈值,若小于则结束折叠计算,得到简化模型,如大于则执行步骤2;
步骤2:对此半边进行折叠,重新计算折叠后的折叠代价,并更新排序队列,返回步骤1。
2.2 折叠代价计算
折叠代价的计算是算法核心,只有优异且准确的代价计算方式才能保证模型轻量化的效率和准确性,同时还要降低算法的复杂程度,本文从顶点三角形平均面积、边曲率变化和折叠边长三个角度组合计算。
2.2.1 顶点三角形平均面积
模型轻量化处理时,应该避免对现实设备几何特征较为明显的部分进行处理,在网格模型中,以同一点为顶点的三角形的平均面积越小,说明此部分网格越密集,也就说明此部分的几何特征越明显,简化时避免对这样的部分进行处理,所以可以将其作为折叠代价计算的一个重要因素。
如图2所示两个网格模型中,同样以v为顶点的三角形总面积的是相同的,但是明显第一个网格模型的三角形数量更多,也就导致以v为顶点的三角形平均面积变小,当对v进行折叠时对模型特征的改变就相对较大,则这样的顶点折叠代价相应变大,计算三角形平均面积的公式如下:

(a) 简化前 (b) 简化后图2 顶点三角形
(1)
式中:count表示以v为顶点的三角形数量,VRi表示其中一个三角形的面积。
2.2.2 模型曲率变化
研究表明,人对曲率大小的感知较为敏感,孪生模型在几何特征不突出即较为平坦的部分曲率较小,而在几何特征突出即棱角、棱边的部分曲率较大,若对曲率较大的部分进行折叠简化,可能会造成模型重要特征丢失,或使得模型变化幅度较大等问题,所以曲率的变化,也是模型简化时需要注意的重要因素[7]。
如图3所示,折叠前后曲率的变化通过所在面法向量的变化来表现,若折叠前后法向量方向变化较大,则代表曲率的变化较大,也就会导致模型特征发生较大变化,可能会造成模型特征的丢失,反之若曲率发生较小的变化,就说明模型特征被较好的保留下来,衡量曲率变化公式如下:
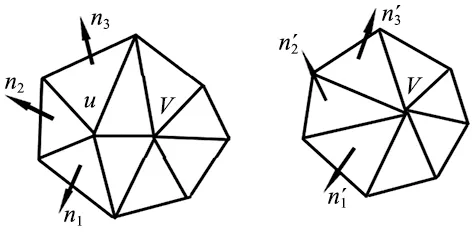
(a) 简化前 (b) 简化后图3 法向量变化
(2)

2.2.3 折叠边长
如果只关注模型特征明显的部分,而大量删减非重要部分,同样会造成模型整体特征发生变化,为了特征区域与非特征区域简化的平衡,引入折叠边边长的折叠代价因子,折叠边边长过长,对此边进行折叠时,就会造成网格模型的大规模变动,所以应该优先考虑边长较短的边进行折叠,公式如下:
d(u,v)=u-v
(3)
式中:u-v为两顶点间的欧氏距离。
2.2.4 折叠代价计算
对以上3点折叠代价因子进行综合考虑,形成折叠代价公式:
(4)
式中,Cost(u,v)为折叠代价。
这样孪生模型得到很好的简化,在实际生产过程中,模型的轻量化保证了物理实体与孪生模型的数据交互和模型显示端的流畅性。
3 模型动作绘制
在完成模型构建、轻量化处理后,为实现并保证数字孪生模型在真实生产过程中可视化和易交互的特性,对整个生产过程中物理设备的动作相对应的模型动作进行绘制。
数字孪生车间实际运行中,将物理设备运行产生的数据,传递给设备数字孪生模型,数字孪生车间系统对数据进行解析,调取相应的模型动作,实现基于实体—模型—数据联用的模型协同,同时使得实体与模型间数据交互速度大为提升[4],满足孪生模型易交互的特性。当需要孪生模型对真实生产进行仿真和预测时,可将预期运行数据先传递给孪生模型,根据数据调取模型动作库中动作,孪生模型进行模拟生产,观测其运行效果和产生数据,效果达标再进行物理设备的真实生产[10]。
预先对模型动作的绘制,能保证在使用、管理过程中,在显示端将模型以直观、可见且流畅的形式呈现,满足可视化的要求。

(5)
式中:任意时间点t∈T,n表示单元零件的数量,对应单元零件的数量。对于任意一个单元零件i,在t时间点上相对于模型运动前状态的运动向量定义为:
(6)

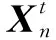
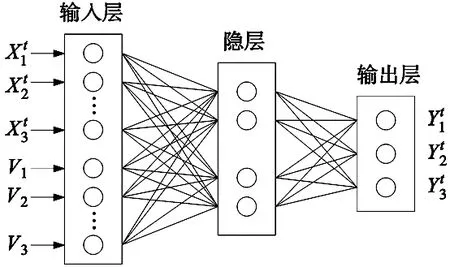
图4 BP神经网络
4 模拟实验及结果展示
4.1 实验环境
在PC机上进行模型建模、模型简化、模型动作绘制操作。
4.2 实验过程
4.2.1 模型建模
首先在blender中对模型最小单元零件建模,如图5所示。

(a) 底座 (b) 连杆臂 (c) 手图5 零件模型

表1 主要部件尺寸 (m)
对零件建模一方面保证了模型每一部分都是准确的,同时在模型需要重构或进化时,只需对部分组件操作即可。模型零件构建完成后根据组装顺序和约束条件对模型组装,组装成如图6所示的完整模型。

图6 完整孪生模型
4.2.2 模型简化
为验证算法的简化效果,在Visual Studio2019上运行算法,对模型进行简化,如图7所示。

(a) 简化前 (b) 简化后图7 模型简化前后网格模型对比图
简化前后图片的对比,展现了在模型主要特征保持完整的情况下,模型几何特征不突出部分的三角形进行了合并,用较少数目的三角形表示更多的信息,使模型的复杂程度减小,表2为简化前后网格模型三角形数据对比。

表2 模型简化前后数据对比
表中数据直观显示了网格明显减少,同时模型的内存大小也得到简化,内存占用大小减少30%,如图8所示。

图8 模型简化前后内存大小变化
4.2.3 模型动作绘制
通过BP神经网络对运动向量偏移的计算,绘制出模型在真实生产中的动作,如图9所示。

(a) 动作一 (b) 动作二图9 模型动作
预先对模型动作的绘制,使得在真实生产过程中只需对传递信号进行解析,调取相对应的动作,保证了显示的同步。
5 结论
数字孪生模型是数字孪生功能的重要保障,本文针对建模、简化、动作绘制的流程进行研究与试验。首先,针对模型最小组成单元零件建模,再根据组装顺序和约束条件对零件组装形成完整的孪生模型,充分实现和保证孪生模型精确化、易进化、易重构的特性;其次,在分析当前主流模型简化算法的前提下,选择采取半边折叠算法,根据折叠因子的计算,进行模型简化,在保证模型功能的基础上,减少数字孪生模型的复杂程度,充分实现模型轻量化的特性;最后,在模型动作绘制时选取BP神经网络解决运动向量迁移问题,保证动作的准确,同时提前对动作的绘制能够保证真实生产过程中虚实交互及显示端的高速,充分实现模型可视化、易交互的特性。进而构造出符合真实生产要求的孪生模型。
