融合A*算法与人工势场法的动态路径规划*

胡 铮,徐 斌

(上海工程技术大学机械与汽车工程学院,上海 201620)

0 引言

动态路径规划是移动机器人研究领域的重要内容之一,是指机器人在有动态障碍物的环境中,如何找到一条从起点到终点的路径,使机器人在运动过程中能安全、无碰撞地绕过障碍物[1]。根据路径规划中环境信息是否已知可将路径规划算法分为全局路径规划和局部路径规划[2]。目前常用全局路径规划算法有:A*算法[3]、粒子群算法[4]以及蚁群算法[5]等。局部路径规划常用的算法有:模糊逻辑算法[6]、人工势场法[7]等。A*算法是一种启发式搜索算法,其实现方法较为简洁,相较于粒子群、蚁群等算法运行效率较高。但是传统A*算法存在拐点多,易斜穿障碍物顶点,路径不平滑等缺点。王玉中等[8]通过合理地设置估价函数的权重比例,缩短算法的运行时间并优化了生成的路径。孔慧芳等[9]通过将转弯修正代价参数加入到启发函数中,从而减少了路径的转弯次数。

当工作环境存在未知障碍物时,一般采用局部路径规划的算法。人工势场法只需要根据周围的环境和当前状态来确定接下来的运动方向,具有计算速度快、路径平滑等优点[10]。但是该方法易在局部极小点陷入停滞,且面对动态障碍物时,传统人工势场法难以达到最优路径指标[11]。为此,徐小强等[12]设置障碍物的预测距离,当机器人在预测距离内将要陷入局部最小时,预先设置虚拟目标点帮助机器人避开陷阱区域。张旭等[13]提出了扇形区域探测法,能够有效地规避动态障碍物。但常规改进的人工势场法很难达到既能在动态环境下高效避障的同时兼具一定的全局最优性。

针对上述的难点,本文提出一种融合A*算法与人工势场法的算法(IA*-APF)。利用改进A*算法规划出的全局路径中的拐点作为改进人工势场法避障的子目标点。实验仿真结果表明,IA*-APF不仅能够有效解决传统人工势场法易陷入局部最小的问题,而且在提高动态环境下的避障效率的同时保证一定的全局最优性。

1 A*算法

1.1 环境模型

机器人的工作环境对其路径规划具有重要的影响,构造环境地图的常用方法主要有栅格法、矢量法和自由空间法等。栅格法是将机器人所处的区域均分为多个方格的一种表示方法。本文采用栅格法创建30×30的栅格模型地图进行实验。在栅格地图中,黑色栅格为障碍物区域,白色栅格为可行区域。

1.2 传统A*算法

A*算法[14]是一种经典的启发式搜索算法。其基本理论是,以机器人的起始节点为父节点,搜索出其周围8个方向的节点,根据估价函数计算它们的f(n)值,选择f(n)值最小的节点为父节点,继续搜索计算,当搜索到目标点时算法结束。最后从目标点沿着父节点反向搜索回到起始节点,获得一条成本最小的路径即为最终路径。A*算法的估价函数f(n)如式(1)所示:

f(n)=g(n)+h(n)

(1)

式中:g(n)为从起始节点到当前节点n的实际代价值,h(n)为启发函数,表示从当前节点到n到目标点的估计代价值。通常h(n)用当前节点n与目标点的欧氏距离来表示:

(2)

式中:xg为目标点的横坐标,yg为目标点的纵坐标,xn为当前节点n的横坐标,yn为当前节点n的纵坐标。

1.3 改进的A*算法

传统A*算法虽能够有效地进行全局路径规划,但其存在着搜索速度慢、易斜穿障碍物顶点且路径冗余节点、拐点较多等缺点,导致机器人路径规划效率低、安全性差。本文旨在从以下3个方面对A*算法进行改进。

(1)改进估价函数。A*算法的搜索效率由启发函数值决定。由于当前节点n到目标点所消耗的h(n)总是小于当前点n到目标点的实际消耗,所以在搜索过程中会搜索过多的节点。如果能够提升估计消耗h(n)的权重,算法的搜索效率将会提高。鲍久圣等[15]提出使用指数函数作为启发函数的加权系数,优化后的估价函数为:

f(n)=g(n)+eh(n)×h(n)

(3)

经过加权改进后,算法的搜索效率有一定的提升,但其搜索范围是父节点周围8个方向的节点,这样会导致一定的无效搜索,算法花费的时间增加。本文在式(3)的基础上,提出基于角度定义的估价函数:

(4)

式中:θi(i=1,2,…,8)为各子节点与父节点及目标点的夹角。若θi不满足式(4)的判断条件,则消除该子节点。改进后的算法与传统A*算法及指数加权A*算法进行对比,结果如图1所示。

(a) 传统A*算法路径 (b) 指数加权A*算法路径

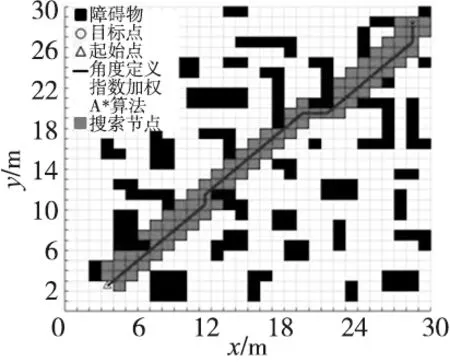
(c) 角度定义指数加权A*算法路径图1 改进A*算法路径对比图

图1中各种算法的数据如表1所示,由此可得,角度定义指数加权A*算法搜索的节点数最少,搜索时间最短,可以有效改善传统A*算法搜索效率低的问题。

表1 改进A*算法路径对比数据

(2)优化子节点的选择。由传统A*算法可知,搜索时f(n)值最小的子节点会成为下一次搜索的父节点,这样的搜索方法忽略了算法的安全性。最终规划的路径有穿过障碍物顶点的现象,机器人与障碍物会有互相碰撞的可能。因此设置障碍物的安全距离对子节点的选择进行优化。判断各障碍物到父节点和各子节点连成的直线的距离是否大于安全距离。若大于,保留该子节点,否则,消除该子节点。对于保留下来的子节点,根据式(4)计算出它们的f(n)值。选择f(n)值最小的子节点为下一次搜索的父节点。通过上述方法对算法进行优化,优化后的路径如图2所示。

由图2可以看出,优化子节点的选择后的算法路径与障碍物之间保持了一定距离,提升了算法的安全性。

图2 优化子节点路径图 图3 二次路径优化路径图

(3)二次路径优化。在图2中,优化子节点后的路径仍存在拐点过多,路径长度较大的问题,因此需要对路径进行二次优化。首先,按顺序提取出路径中所有拐点,起始节点和目标点也看作拐点;接着,连接拐点与其不相邻的后续拐点得到一条新的路径,以该新路径的f(n)值是否小于原路径的f(n)值以及其是否在障碍物的安全距离外作为该新路径是否成立的判断标准。如果新路径成立,则剔除中间拐点,否则,保留原路径;最后,生成的路径为最短路径。二次路径优化后的结果如图3所示。

表2为路径二次优化前后的数据对比,可以看出,二次路径优化减少了路径中的拐点和路径长度,有效地简化了路径。

表2 路径数据对比

2 人工势场法

2.1 传统人工势场法

传统人工势场法[16]的主要原理是梯度势场法。在算法中,机器人受到的引力势场为:

(5)

式中:m为引力增益常数,ρ为目标点与机器人的距离。机器人受到的引力为引力势场函数的负梯度:

Fatt=-▽Uatt=mρ

(6)

机器人受到的斥力势场为:

(7)

式中:k为斥力场常量,q为机器人与障碍物的距离,λ为障碍物对机器人的影响距离。机器人受到的斥力为斥力势场函数的负梯度:

(8)

传统人工势场法通过引力与斥力的合力大小与方向控制机器人运动,对于只存在静态障碍物的环境能够快速规划出一条无碰撞路径,但是在复杂动态的障碍物环境中,其往往无法满足规划要求。本文通过改进人工势场法的斥力函数来解决这一问题。

2.2 改进人工势场法

动态路径规划中视机器人为质点,其运动方向为其合力的方向,速度的大小为步长。当传统人工势场法在动态环境中进行路径规划时,并没有考虑机器人与障碍物的位置和相对运动速度的关系,导致规划的路径变长,导航效率降低。为了在动态环境下提高机器人的导航效率,在斥力函数中加入相对速度斥力。改进后的斥力势场为:

(9)

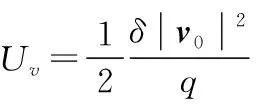
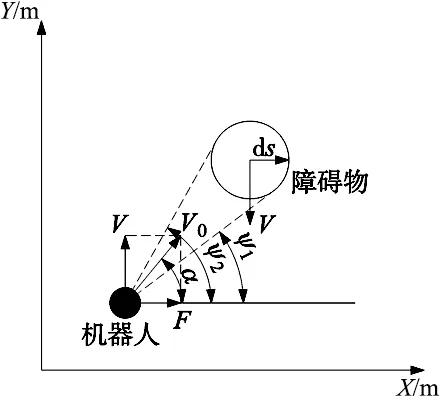
图4 机器人与动态障碍物有碰撞风险

改进斥力势场后相应的斥力Frep1为:

(10)

相对速度斥力的方向与动态障碍物对机器人的斥力方向一致。引进相对速度斥力可以让机器人在与动态障碍物有碰撞风险时获得更大的斥力,在相对安全的状态下可以避免盲目的避障。

2.3 改进A*算法结合人工势场法

A*算法通过上述的改进之后可以有效解决搜索效率低和避障安全性等问题,能在已知环境下规划出一条全局最优路径。人工势场法在上述改动中可以有效解决动态环境中的避障问题。由于A*算法具有全局最优性,人工势场法具有避障的实时性。本文将两种改进算法相结合,提出的IA*-APF算法的流程图如图5所示。

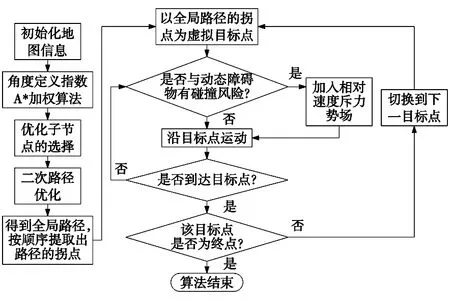
图5 IA*-APF算法的流程图

在IA*-APF算法中,改进A*算法在已知的障碍物环境中进行全局路径规划,全局路径的拐点依次作为人工势场法的路径规划的虚拟目标点,直至到达终点算法结束。

3 算法仿真与结果分析

为了验证IA*-APF的可行性,本文构造陷阱区域和动态障碍物环境进行仿真研究,仿真基本参数如表3所示。

表3 仿真参数设定

3.1 陷阱区域环境下的实验结果

在30×30的栅格地图中随机创建障碍物,在障碍物中随机设置如U型、L型等局部陷阱区域。机器人的起始点为(3,2),目标点为(17,20)。图6为传统人工势场法与IA*-APF在陷阱区域环境下的避障结果。

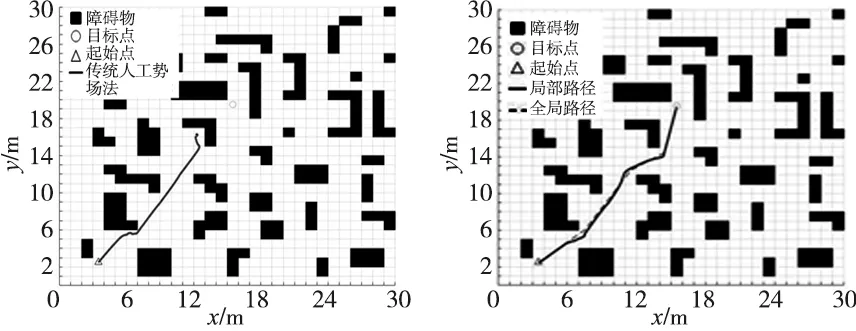
(a) 传统人工势场法避障路径图 (b) IA*-APF算法避障路径图图6 存在陷阱区域的环境路径对比

如图6a所示,传统人工势场法在避障过程中遇到L型障碍物陷阱,机器人在陷阱障碍物内部陷入局部最小,无法避开障碍物。在图6b中,IA*-APF中全局路径的拐点作为局部路径的虚拟目标点,帮助机器人逃离陷阱区域。

3.2 动态环境下的实验结果

为了进一步验证IA*-APF算法求解动态路径规划问题的有效性,在陷阱区域环境的基础上,增加动态障碍物进行实验仿真。环境1为单个动态障碍物混合静态障碍物,动态障碍物的起始点为 (25,13),其运动速度分别为vobs1=[-0.35,0.35]。环境2为多个动态障碍物混合静态障碍物,在环境中随机设置3个动态障碍物,它们的起始点分别为(9,13),(15,21),(19,9),运动速度分别为vobs2=[0.5,0],vobs3=[0,-0.5],vobs4=[0.6,0]。将IA*-APF算法与文献[17]算法、传统人工势场法进行比较,结果如图7和图8所示。图中的箭头表示障碍物的运动方向,深灰色×代表动态障碍物的起始点,以×为顶点的深灰色线条表示障碍物的运动轨迹。

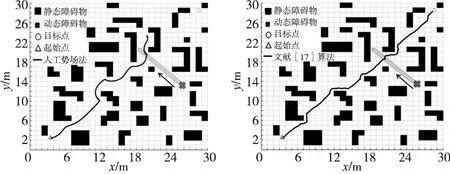
(a) 传统人工势场法的路径结果 (b) 文献[17]算法的路径结果

(c) IA*-APF的路径结果图7 环境1的算法路径对比

(a) 传统人工势场法的路径结果 (b) 文献[17]算法的路径结果

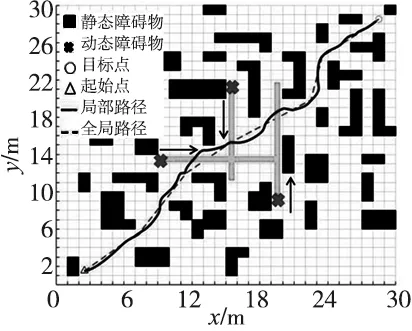
(c) IA*-APF的路径结果图8 环境2的算法路径对比

由图7的实验结果可以看出,传统人工势场法在动态环境一中因避障幅度过大以至于陷入陷阱区域,无法完成避障任务。文献[17]算法虽能成功到达目标点但路径转折较多。在图8的实验中,传统人工势场法和文献[17]算法在面对动态障碍物时陷入徘徊状态。而IA*-APF在两种环境中既能较好地避开动态障碍物又能保持一定的全局最优性。

表4得出了3种算法在两个不同环境下的实验仿真结果,在实验环境1中,IA*-APF的步数、路径长度以及运行时间均略优于文献[17]算法。在实验环境2中,IA*-APF相较于传统人工势场法,步数减少25%,路径缩短25.6%,运行时间缩短14.8%,相较于文献[17]算法,步数减少12.4%,路径缩短12.6%,运行时间缩短7.4%。

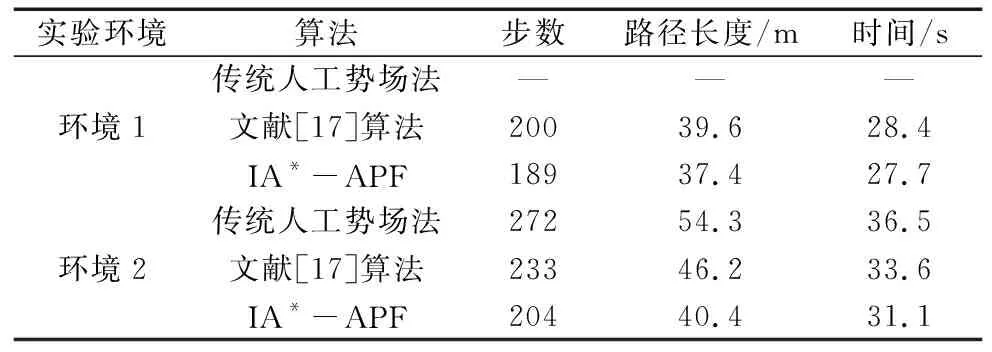
表4 动态环境下的算法数据

4 结束语

针对移动机器人动态路径规划问题,提出了一种改进A*算法与人工势场法的混合算法。首先在传统A*算法的基础上,提出基于角度的加权估价函数和利用障碍物的安全阈值优化子节点的选择策略,然后对路径进行二次优化,提高了算法的路径规划效率和安全性。为了能让机器人的动态路径规划更加高效,在人工势场法的斥力函数中引入相对速度斥力函数。利用改进A*算法得到的全局路径的拐点作为人工势场法避障的子目标点。陷阱区域和动态环境下实验结果表明, IA*-APF算法可以有效地避开局部极小陷阱区域,且在动态未知的环境中能规划出一条安全的、高效的路径的同时保持一定的全局最优性,为移动机器人在动态环境下的避障提供了理论基础。