基于数值模拟的柴油机连杆螺纹联接可靠性分析*

胡丰岩,何 强,周宏根,符博峰,赵 明,杨 平

(1.江苏科技大学机械工程学院,镇江 212003;2.陕西柴油机重工有限公司,西安 713100)

0 引言

柴油机作为运用最广泛的动力输出机械之一,对工程机械及交通运输领域的发展有重要的影响。因此提高柴油机可靠性、实现轻量化、降低燃油消耗率等都成为设计师们努力的目标[1]。连杆机构是柴油机中结构最为复杂、承受载荷最大的结构之一,螺纹联接结构又是连杆部分的主要部件之一,不恰当的螺纹联接设计会造成连杆机构的失效,从而影响柴油机的正常运转[2-4]。因此研究螺纹联接的结构参数对其联接强度的影响有着重要的工程意义。

目前而言,对于螺纹联接结构应力分布的研究方法主要有:理论分析法、实验探究法以及有限元仿真法。由于理论分析法和实验探究法会受到实际情况的限制,所以目前应用最广泛的就是采用有限元软件对模型进行仿真分析[5]。同时也有很多人采用有限元方法对螺纹联接结构进行分析。MARUYAMA[6]通过有限元计算出拧入螺母的螺栓螺纹的载荷分布,采用有限元仿真方法计算出了标准螺纹在轴向力作用下的应力受影响的规律;LEHNHOFF等[7]建立螺栓联接的轴对称有限元模型,通过有限元方法研究螺栓与连接件之间的刚度。卢耀辉等[8]通过对柴油机连杆螺栓的预紧力工况和最大拉伸工况的强度分析,利用Goodman疲劳曲线对其疲劳强度进行评定以便于准确的找到疲劳失效部位,为螺栓的抗疲劳设计提供了参考。

本文以某型柴油机连杆螺栓作为参考,建立了不同螺距、螺纹连接长度和螺栓预紧力的三维有限元连杆螺栓模型,对其进行网格划分以及边界条件的施加;研究了不同因素对螺纹连接结构轴向应力分布的影响,结果表明螺栓的应力主要集中在螺纹联接的第一螺纹连接处,且不同因素对螺栓应力集中有着重要的影响。

1 连杆螺纹联接结构以及工作载荷的分析

1.1 连杆螺纹联接结构的分析

本文采用某型柴油机连杆螺纹联接结构作为主体研究对象,由于本文主要研究螺纹联接部分的结构,因此对连杆大头螺纹连接的一侧进行拆分,选取螺纹联接结构局部模型进行单独的研究,实体模型如图1所示。

计算选取M16-80的三角形螺纹螺栓,采用的相关设计标准为GB/T 31.3-1988和ISO 7412,性能等级为10.9级,公称直径为8 mm,螺距为1.25 mm,内螺纹牙数为11,外螺纹牙数为10,啮合10牙。

1.2 连杆螺纹联接结构工作载荷的分析

连杆螺栓螺纹联接属于紧联接,连杆大头螺栓在运动的时候主要承受螺栓预紧力、活塞连杆部分的往复惯性力和连杆大头端回转部分质量的离心惯性力。由于螺栓受力较为复杂,这里将螺栓的负荷变形情况用平面图表示。如图2所示。

图2 连杆螺栓受力过程变形与应力关系图

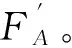
(1)螺栓预紧力计算。连杆螺纹联接部分主要受到螺栓预紧力和活塞连杆部分的往复作用力。预紧力的大小决定了柴油机连杆螺栓的安全余量和疲劳载荷的变化范围,对柴油机连杆螺栓的寿命有着很大的影响。连杆螺栓预紧力的计算方法如下:

(1)

式中:E为螺栓的弹性模量,取值为2.1×105MPa;A为螺栓伸长部分的截面积,杆身直径为16 mm,计算得A为200.96 mm2;ε为螺栓伸长量,取值为0.4 mm;l为螺栓受拉力拉伸部分长度,取杆身长度80 mm。通过计算得到F=2.11×105N。

(2)最大拉伸载荷计。连杆的最大拉伸载荷出现在曲轴转角φ=0°的时候,计算方法如下:

(2)

式中:G′为活塞组的重量,G1为连杆组往复部分的重量,G2为旋转部分的重量,G3为连杆大头盖的重量,λ为曲轴连杆比,i为气缸数。

2 连杆螺纹联接结构有限元分析

2.1 螺纹联接结构有限元网格的划分

本文通过SolidWorks进行连杆螺栓三维模型的建立,如图1所示,建立完成后另存为Parasolid文件格式,导入到ANSYS中Workbench的静态结构分析模块。采用Workbench自带网格划分功能,设置整体的网格尺寸为1 mm,螺纹联接处的网格尺寸为0.25 mm,跨角度中心的网格尺寸为中等。划分得到的实体有限元模型包含130 715个单元和293 266个节点。网格划分结果如图3所示。

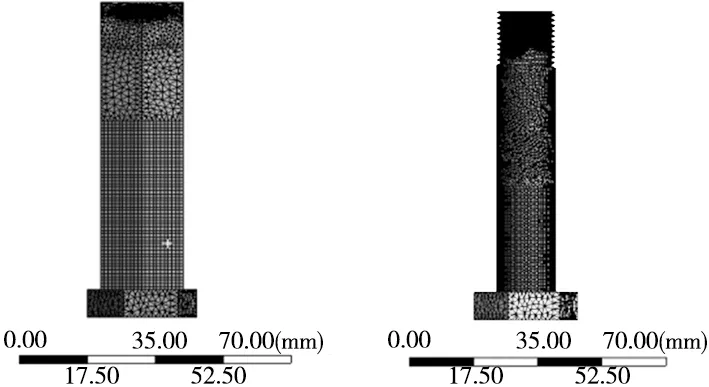
图3 螺纹连接处网格划分示意图

2.2 螺纹联接结构边界条件的确立

(1)接触条件设置。本文的螺纹联接主要涉及到4个接触面,其中连杆大头端盖与连杆小头、螺栓头部和连杆大头盖接触、螺栓和连杆孔的接触设置为绑定接触;螺栓外螺纹和连杆内螺纹的接触设置为摩擦接触,摩擦系数为0.15。

(2)材料参数设置。本文中选取的柴油机连杆螺纹规格为M16×2,材料选择42CrMo,材料的抗拉强度为1080 MPa,屈服极限为830 MPa,泊松比为0.3。弹性模量为210 GPa。

(3)边界条件的施加。将螺纹连接部分分为两个工况进行有限元静态强度的分析:

预紧力工况:即研究螺栓在仅受到螺栓预紧力的情况下的应力分布情况。

最大拉伸工况:螺栓受到连杆交变载荷的最大拉伸力,同时受到螺栓预紧力的约束。

在分析两种工况的同时,要在螺栓的小头部分施加一个固定约束,这是为了保证螺在在有限元计算的过程中不会发生过大的形变,也使得仿真结果更贴合于实际情况。边界条件施加示意图如图4所示。

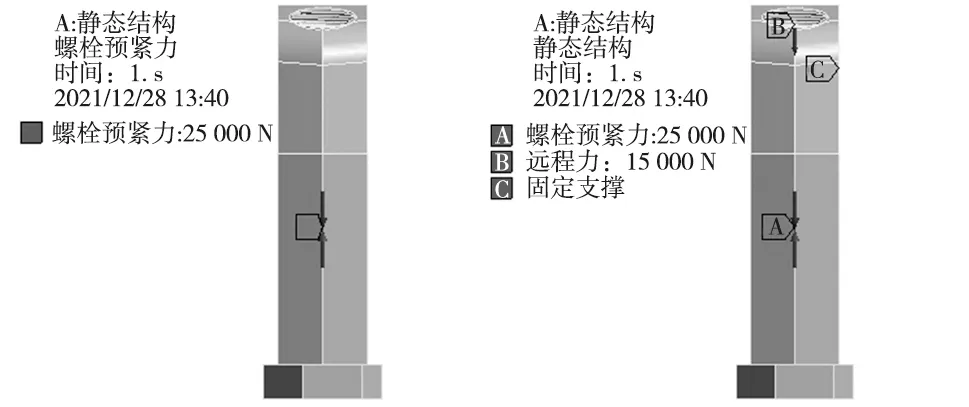
(a) 预紧力工况边界条件示意图 (b) 最大拉伸工况边界条件示意图图4 螺栓边界条件示意图

2.3 连杆螺纹联接结构有限元结果分析

通过前文对连杆螺栓做的联结结构分析以及对螺纹联结结构的有限元计算。本节主要从预紧力工况和最大拉伸载荷工况两个方面对连杆螺栓螺纹联接进行有限元分析。

(1)预紧力工况。在预紧力工况下,对应螺栓实际工作中的最小载荷工况,这时仅对螺栓施加螺栓预紧力,图5是该工况下螺栓和螺纹联结结构的变形情况。

(a) 螺栓变形结果图 (b) 螺栓Von-Mises图图5 预紧力工况螺栓位移及Von-Mises示意图

图5a是螺栓的受力变形位移图,可以看出螺栓的最大位移发生在螺栓的中间位置大小为4.59×10-5m。图5b是螺栓的等效应力图,最大应力发生在一级螺纹位置处大小为863.54 MPa。

(2)最大拉伸工况。最大拉伸工况下螺栓受到残余预紧力和最大拉伸载荷的作用力。在此工况下,螺栓在螺纹头部过渡位置产生了应力集中。最大应力发生在一级螺纹位置处,大小约为902.14 MPa。连杆螺栓的两端受力较小,具体的等效应力分布如图6所示。

图6 最大拉伸工况螺栓Von-Mises示意图

由图6可以看出,在螺栓与连杆大头接触的面受力比较均匀,接触受力较小,在螺纹连接处受力较为集中,比较容易发生磨损甚至是断裂的情况。

3 连杆螺纹联接结构应力分布影响因素研究

通过无量纲法对螺纹联接结构进行参数定义,采用有限元仿真方法开展了螺距、螺纹连接长度、螺栓预紧力对螺纹连接结构可靠性的影响,为合理设计螺纹联结结构提供可靠参考。

3.1 螺距对螺纹联接结构应力分布的影响

以上文构建的连杆螺栓为基础,通过改变螺纹联结的螺距来探究不同的螺距对螺纹联结结构应力分布的影响。本章主要设置了4个螺距的螺纹联接方案来研究,螺距分别是1 mm、1.25 mm、1.5 mm和2 mm。通过将图7的模型导入有限元仿真软件中,对其进行计算,得到不同螺距的螺纹联接结构应力的分布情况,如图7所示。

(a) 1 mm (b) 1.25 mm

(c) 1.5 mm (d) 2 mm图7 不同螺距模型Von-Mises图

由图7可知不同螺距的螺栓最大应力基本相差不多,应力也都集中在螺纹联接和螺栓螺杆处,尤其是前面几级螺纹处;而且因为受到轴向分力的影响,螺纹的齿根处受到了较为明显的应力集中。由于不同螺距的应力结果梯度相差不大,可以看出随着螺纹螺距的增加,应力集中的区间也随着扩大。螺距为1 mm、1.25 mm、1.5 mm的螺纹联接处的应力主要为100～400 MPa左右,螺距为2 mm的螺纹应力主要为200～600 MPa左右。

从螺纹牙处分析,内外螺纹牙底主要受到拉应变,而牙根处受到交替的拉压力,且承受的压力数值较大,容易发生疲劳失效。

3.2 螺纹联接长度对螺纹联接结构应力分布的影响

在连杆螺栓中,螺纹联接结构是最重要的部件之一,本章在常规螺纹联接长度的基础上,在一定合理的范围内,自定义了另外3个螺纹联接长度,分别是4.5 mm、12 mm、15 mm和22.5 mm。将三维模型导入有限元软件中进行分析计算,得到的Von-Mises图如图8所示。

(a) 4.5 mm (b) 12 mm

(c) 15 mm (d) 22.5 mm图8 不同螺纹联接长度Von-Mises图

由图8所示,整体观察螺栓的应力分布,发现靠近第一级螺纹联接处的应力较大且较为集中,随着远离第一螺纹处应力开始逐步的下降。由此可以看出不同的螺纹联接长度应力集中的主要位置都在前几级螺纹处,但是螺纹联接长度较小的螺纹联接结构应力集中尤为严重。4.5 mm的螺纹应力集中位置大小主要在500～700 MPa左右,另外3个应力集中区域大小主要在300～500 MPa左右。

3.3 螺栓预紧力对螺纹联接结构应力分布的影响

螺栓在工作的状态下,连杆的大头部分会受到持续往复的拉伸和压缩载荷的作用力,如果受到的热载荷的作用力,还会导致螺纹联接出现松动。因此需要施加一个合适的螺栓预紧力来提高螺纹联接的可靠性、防松能力和螺栓的疲劳强度,增加联接的紧密性和刚性。大多数的实验证明较高的预紧力对螺纹联接结构的可靠性和使用寿命都是有益的,当然过高的预紧力如果控制不好也会导致螺纹联接的失效。

根据上文计算出的螺栓预紧力F为参考,因为实际工作中多为预紧力不足的情况,在这里分别设计螺栓预紧力P0为0、1/5F、2/5F、3/5F、4/5F和F六种方案。

将模型通过有限元软件计算分析,得到螺纹的Von-Mises图,结果如图9所示。

(a) P0=0 (b) P0=1/5F

(e) P0=4/5F (f) P0=F图9 不同螺栓预紧力Von-Mises图

由图9可以看出,在其他条件不变的情况下螺纹的Von-Mises随着螺栓预紧力的增大,应力集中区间的应力大小相应的减小,螺纹处的承载比例也在相应的降低,这也证实了较大的螺栓预紧力可以提高螺纹联接的可靠性,防止螺纹联接出现松动损坏等情况。为了更加明确的显示螺栓预紧力对螺纹联接结构的影响,本文从有限元结果中提取了不同螺栓预紧力和不同位置螺纹承载比例的关系,具体如图10所示。

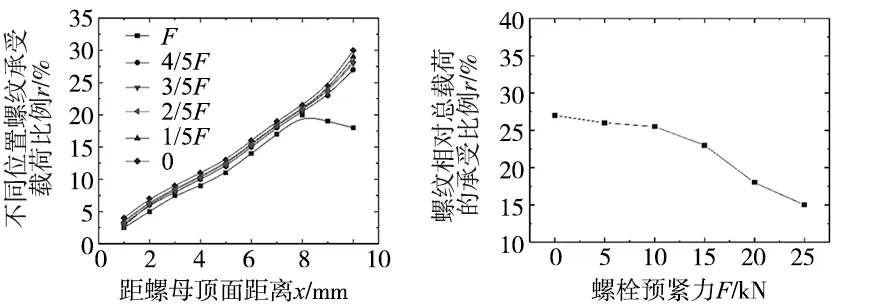
(a) 不同位置螺纹承载比例与螺栓预紧力的关系 (b) 螺纹相对总载荷承受比例与螺栓预紧力关系图图10 螺栓预紧力与不同位置螺纹承载比例关系图

由图10a所示,在不考虑螺栓预紧力的情况下,螺纹处距离螺母越远,它的承载比例就越高,特别是在第一螺纹处,承载比例最高。在不同螺栓预紧力条件下,螺纹各处的承载比例随着螺栓预紧力的增大而下降。特别是在P0为F的情况下,从距离螺母超过8 mm开始,螺纹开始进入塑性状态而塑性偏差大于弹性偏差;图10b表示的是螺纹相对总载荷承受比例与螺栓预紧力的关系,可以看出,随着螺栓预紧力的增加,各螺纹承载比例跟随着有所下降。

4 螺纹联接疲劳可靠性分析

4.1 疲劳评定方法

对于螺纹联接这种承受交变载荷的机械结构,可以使用修正的Goodman曲线进行评定。Goodman曲线是指受交变应力的零件,在等寿命的条件下,其平均应力与最大应力和最小应力的关系曲线。在评估疲劳强度的时候,任何位于Goodman疲劳曲线封闭区域之外的结构点都代表着结构发生了疲劳破坏。图11为Goodman疲劳曲线图。

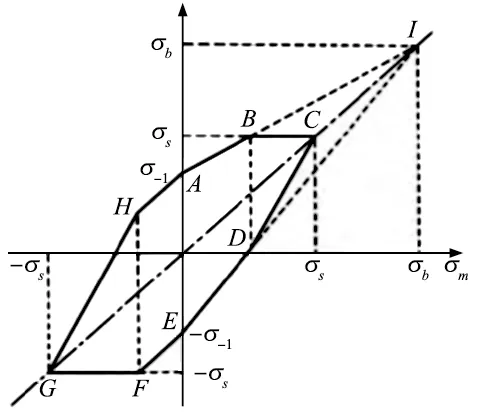
图11 Goodman疲劳曲线

图11中,ABCDEFGHA所形成的密闭区域则为Goodman疲劳曲线,横坐标表示平均应力,纵坐标表示最大最小应力。

4.2 疲劳评定结果

通过第3节的应力仿真结果分析,选取螺纹联接长度为12 mm,螺距为1.25 mm的螺纹进行疲劳仿真。将选取好的模型及应力分析结果导入Ansys nCode Design-Life软件。图12为螺纹的疲劳仿真结果。

(a) 螺纹疲劳寿命图 (b) 螺纹损伤图

(c) 螺纹安全系数图 (d) 螺纹疲劳等效应力图图12 螺纹疲劳仿真结果图

根据Goodman疲劳强度疲劳法则,螺纹损伤低于1,螺纹安全系数要大于1则满足要求,由图中结果可得该螺纹的强度符合该法则。

4.3 不同螺栓预紧力对螺栓疲劳寿命的影响

为了探究螺栓预紧力对螺栓联接结构的影响,通过设置6种工况来分析不同预紧力下螺栓的疲劳寿命情况。即预紧力为0、1/5F、2/5F、3/5F、4/5F和F六种方案。6种工况疲劳寿命计算结果如图13所示。

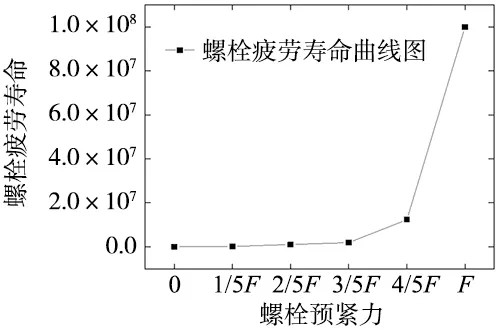
图13 不同螺栓预紧力作用下螺栓疲劳寿命曲线图

由图13可知,在不施加预紧力的情况下,连杆螺栓疲劳寿命最短,随着预紧力的增加,螺栓的疲劳寿命也随之增长,当达到期望的螺栓预紧力的时候,螺栓的疲劳寿命也达到最高。可见较高螺栓预紧力可以提高螺栓联接的可靠性和使用寿命。

5 结论

本文采用有限元仿真方法对柴油机连杆螺纹联接结构进行静强度特性分析,通过研究不同螺距、螺纹联接长度和不同螺栓预紧力对螺纹联接结构应力分布以及螺纹承载比例影响,最后通过疲劳分析结果验证了设计参数对于联接结构设计的重要性,主要的研究成果如下:

(1)在进行有限元仿真分析时,充分的与实际相结合,合理的建模和设置材料参数以及边界条件,这样可以使得仿真得到的结果更贴合实际。结果表明连杆螺栓的应力集中主要发生在第一螺纹联接处,如果从单个螺牙的角度分析,则是螺纹根部应力集中较为严重。

(2)在研究螺距、螺纹联接长度和螺栓预紧力对螺纹联接结构的影响时发现,随着螺距的增大、螺纹联接长度的减小以及螺栓预紧力的减小,螺纹发生应力集中的情况就更严重,同时,螺纹处所承受的载荷比例也随着增高。

(3)通过一系列的分析对比,证实了设计参数对于螺纹联接结构设计的重要性,合理的结构参数可以提高工件的使用寿命,降低其损坏率。本文为螺纹联接结构的设计提供了参考数据。