烟丝压缩过程中应力松弛模型的建立

韩顺起，付丽丽，丁 伟，张 柯，郑松锦，李 铭，彭译娇，黄 刚，刘 泽，王 兵*，李 斌

1. 中国烟草总公司郑州烟草研究院，郑州高新技术产业开发区枫杨街2 号 450001

2. 浙江中烟工业有限责任公司杭州卷烟厂，杭州市转塘街道科海路118号 310012

3. 河北中烟工业有限责任公司技术中心，石家庄市桥西区工农路360号 052165

4. 广东中烟工业有限责任公司湛江卷烟厂，广东省湛江市赤坎区康乐路7号 524033

5. 山东中烟工业有限责任公司青州卷烟厂，山东省青州市玲珑山北路1818号 262500

6. 云南中烟工业有限责任公司技术中心，昆明市五华区红锦路181号 650231

高速卷制的烟支质量依赖于烟丝堆积体的力学性能。目前烟草行业内也有很多表征烟丝力学性能的方法，通常使用质构仪来评价片烟及再造烟叶的力学性质，如柔软性、黏附力等，但是该方法主要用于单个片烟力学性质的评价，不能准确评价烟丝堆积体的力学性质。对于烟丝堆积体，常用填充值来表征烟丝的填充能力，填充值是单位质量烟丝所占的体积，是一个静态值，并不能准确反映烟丝在卷制过程中先压缩后松弛动态过程的力学变化，不同烟丝填充值差异的根本原因是烟丝的流变学性质不同。卷烟的卷制过程可以看作是烟丝压缩后烟支体积保持不变，烟丝弹性恢复力随时间减小的应力松弛过程。此过程中，应力不能松弛到零，最终存在平衡应力，该平衡应力就是烟丝对于卷烟纸的作用力的直观反映。因此，揭示烟丝压缩后应力松弛规律及获得流变学参数具有重要意义。

目前国内外学者基于流变学理论，通过闭式压缩装置，对不同种类的农业物料进行了蠕变-应力松弛试验研究，发现农业物料不同于理想的弹性或黏性材料，属于黏弹性材料，在压缩和松弛过程中表现出特有的流变特性［1-2］，应力松弛规律受压缩载荷及被压物料性状等因素的影响［3-7］。房佳佳等［8］利用残数法确定了紫花苜蓿应力松弛过程中的流变学模型为五元件广义Maxwell模型，研究了样品量、压缩频率、含水率对流变学参数的影响。李旭英等［9］发现三元件Maxwell 模型可以准确描述牧草的应力松弛规律，并得出牧草的应力松弛时间、弹性模量是物料本身固有的，不受外部条件的影响。廖娜等［10］使用两个Maxwell 元件和一个弹簧并联的五元件广义Maxwell 模型描述玉米秸秆在闭式压缩容器内的应力松弛过程，并得到了玉米秸秆在该过程中的流变学参数。Ryszard等［11］对稻草进行重复压缩，利用经典流变学模型考察了每次压缩后的应力松弛规律，发现弹性模量与荷载成正比，且随应变循环次数的增加而减小。Guo等［12］采用分数阶模型描述马铃薯块茎的松弛行为，发现该模型和广义Maxwell 模型都能对马铃薯块茎进行准确模拟。很多学者已经对农业物料压缩过程中的应力松弛行为做了大量的试验研究，并得出了对应的流变学模型及流变学参数［13-17］，但关于烟丝的应力松弛行为研究尚未见报道。因此，以烟丝为研究对象，采用闭式压缩的方式进行试验，根据压缩过程中的应力松弛数据，建立了符合烟丝应力松弛行为的流变学模型，并分析了不同压缩力、样品量对烟丝流变学参数的影响，旨在为烟丝填充能力的表征提供方法。

1 材料与方法

1.1 材料与仪器

试验样品为浙江中烟工业有限责任公司“利群”品牌配方烟丝，于掺配生产线上获取。将样品烟丝置于温度（22±1）℃、相对湿度60%±2%的环境中平衡48 h。

WKX204电子天平（感量0.000 1 g，瑞士Mettler Toledo 公司）；烟丝压缩流变测试仪（中国烟草总公司郑州烟草研究院），其结构示意图如图1所示，通过计算机实时采集试验过程中样品的应力、位移、时间等数据。

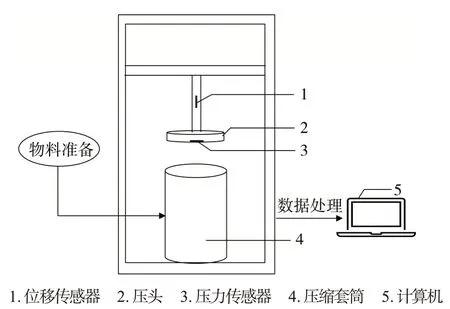
图1 烟丝压缩流变测试仪的结构示意图Fig.1 Schematic diagram of a cut tobacco compression rheological tester

1.2 方法

应力松弛过程实质是保持样品压缩后体积不变，不可逆变形逐步取代弹性变形，使烟丝的弹性恢复力随时间逐渐减小的过程。烟丝属于黏弹性物料，完全用理论性的数学分析和计算方法对其应力松弛过程进行研究比较困难。对于农业物料，通常采用试验方法研究，即通过试验获取其应力松弛曲线，利用经典的流变学模型对试验所得的应力松弛曲线进行回归拟合，然后求解对应的模型参数。

1.2.1 试验设计

首先，将试验样品烟丝缓慢装入烟丝压缩流变测试仪的压缩套筒内，保持其自然堆积状态，样品量为15 g。压缩过程中压头下压速度为1 mm/s，最大压缩力为3 kg，达到最大压缩力后压头位置保持不变，保压时间为200 s。通过数据采集系统获得松弛应力与时间的测试数据，每个样品在相同试验条件下测试3次，结果取平均值。

1.2.2 应力松弛模型的选择

农业物料流变学模型一般由3个基本元件组成：弹簧、阻尼器和摩擦块，分别表征物料的弹性、黏性和塑性。对于松弛过程，一般以Maxwell 模型为基础（图2），通过不同的串并联组合构成了描述应力松弛过程的一些经典模型。

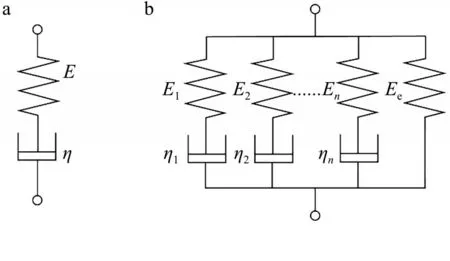
图2 Maxwell 模型（a）及广义Maxwell 模型（b）Fig.2 The Maxwell model（a）and a generalized Maxwell model（b）

Maxwell 模型由一个弹簧元件和一个阻尼元件串联而成，如图2a所示。在受到载荷作用时，弹簧元件首先发生瞬时形变，在系统形变量保持不变的过程中，在阻尼元件的作用下，弹簧元件的弹性恢复力不断衰减，同时，阻尼元件受弹簧元件的推力作用，发生黏性位移，位移速率逐渐减小，最终弹簧元件完全恢复形变，阻尼元件的黏性位移量等于初始弹簧元件被压缩的形变量，此时，系统达到平衡。烟丝内部的应力松弛过程通过Maxwell 模型的表征，可以解释为在一定形变量下，烟丝内部的弹性形变转变成黏性流动的过程。其本构方程为：

式中：t为时间（s）；σ（t）为在t时刻系统的应力（kPa）；ε0为烟丝的初始应变量；E为Maxwell模型中弹簧的弹性模量（kPa）；η为Maxwell 模型中阻尼器的黏性系数（kPa·s）。

对于农业物料的应力松弛过程，一般以Maxwell模型为基础，结合试验所得应力松弛曲线分析，用广义Maxwell模型描述（图2b），并联多少Maxwell模型以及是否并联弹簧需要根据具体的试验数据分析确定［9］。

烟丝压缩过程中，烟丝内部的应力不能全部松弛，存在一定的平衡应力。平衡应力在模型中可用一个并联的弹簧表示［1］，在应力松弛过程中不可恢复。因此，选用一个n阶Maxwell 模型和一个弹簧元件并联组成的广义Maxwell 模型对烟丝应力松弛曲线进行模拟，根据拟合效果确定n的值。结合参考文献，首先选择三元件和五元件Maxwell 模型进行分析。三元件和五元件Maxwell 模型如图3所示。

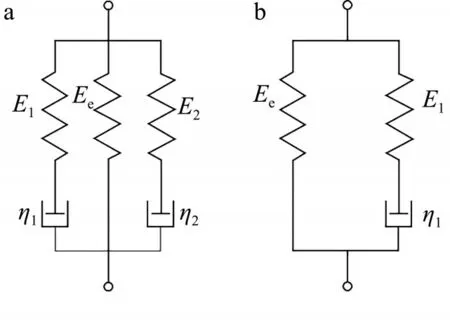
图3 五元件广义Maxwell模型（a）和三元件广义Maxwell模型（b）Fig.3 A five-element generalized Maxwell model（a）and a three-element generalized Maxwell model（b）

其中三元件广义Maxwell 模型由一个Maxwell元件和一个弹簧并联而成（图3b），其应力松弛本构方程为：

式中：E1、Ee分别为Maxwell 元件中的弹簧和并联弹簧的弹性模量（kPa）；T1为Maxwell 元件的应力松弛时间（s），T1＝η1/E（1s）。

五元件广义Maxwell 模型由两个Maxwell 元件和一个弹簧并联而成（图3a），其应力松弛本构方程为：

应力松弛的快慢取决于起始应力和对应应力松弛时间的比值，可以用应力松弛时间比率α表示［1］：

式中：α为起始应力在单位时间内松弛的量（kPa/s）；表示每个Maxwell模型起始应力和对应应力松弛时间的比值。

2 结果与分析

2.1 蠕变-应力松弛曲线

根据所得实验数据，绘制烟丝压缩过程中的蠕变-应力松弛曲线，如图4所示。根据农业物料的蠕变松弛特性，可将该过程分为4 个阶段，第1 阶段（AB段）为蠕变阶段，该阶段烟丝在压头的作用下由松散变为致密；第2阶段（BC段）为应力突降期，因为烟丝被压缩变形（包括弹性变形和黏性变形），当压头停止瞬间烟丝作用在压头上的力只剩下弹性恢复力，该过程骤降的力以突降应力表示；第3 阶段（CD段）为应力快速衰减期，主要发生在应力松弛开始的前60 s内；第4阶段（DE段）为应力缓慢衰减期，此阶段应力松弛的速率明显减慢，直至平衡。本实验中主要研究后两个阶段（应力松弛阶段）。

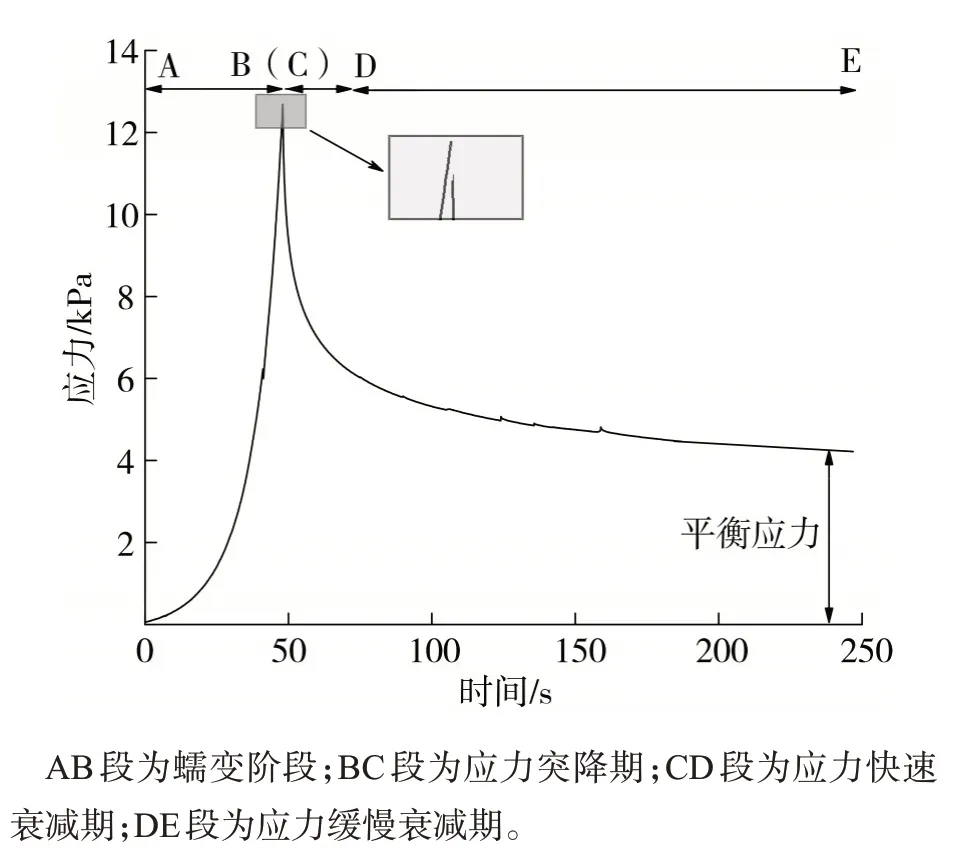
图4 烟丝蠕变-应力松弛曲线Fig.4 Creep-stress relaxation curve of cut tobacco

2.2 模型稳健性分析

2.2.1 两种模型模拟对比分析

根据公式（2）和公式（3），对不同样品量和不同压缩载荷条件下的烟丝应力松弛数据进行拟合，三元件和五元件广义Maxwell模型的拟合结果如图5～图8所示。由图5～图8可知，采用三元件广义Maxwell模型拟合烟丝的应力松弛曲线，其决定系数R2=0.927~0.942，而五元件广义Maxwell 模型拟合曲线的决定系数R2=0.994~0.996。由图5～图8可见，五元件广义Maxwell 模型的模拟效果明显优于三元件广义Maxwell模型。为提高拟合精度，也可继续并联Maxwell元件，但考虑到五元件模型对应力松弛试验数据的拟合相关系数均达到0.994以上，满足了所需精度，无需继续增加模型的复杂度。因此，选用五元件广义Maxwell 模型对烟丝的应力松弛过程进行模拟。

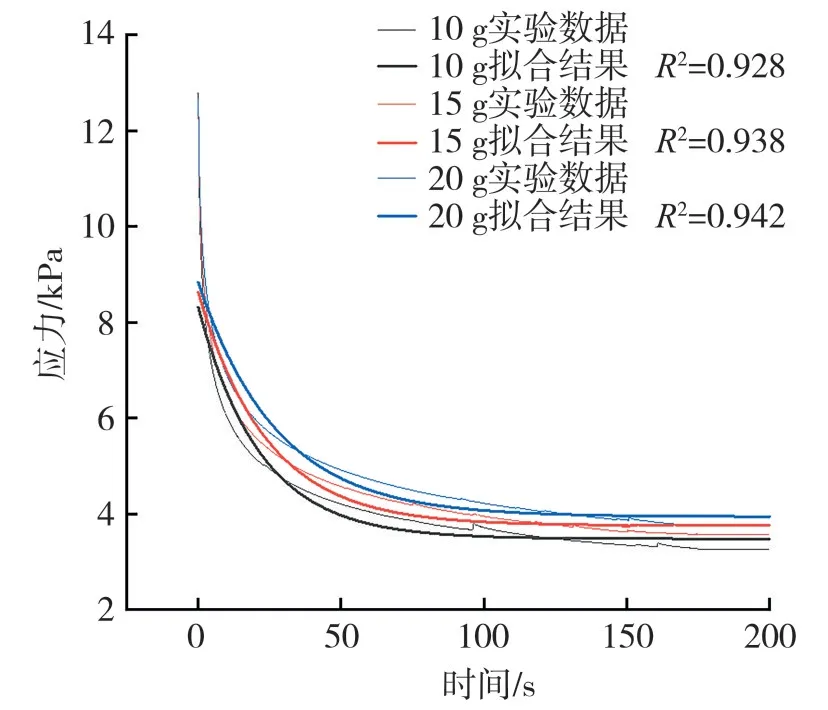
图5 不同样品量下三元件广义Maxwell模型拟合曲线Fig.5 Fitting curves of the three-element generalized Maxwell model under different sample amounts

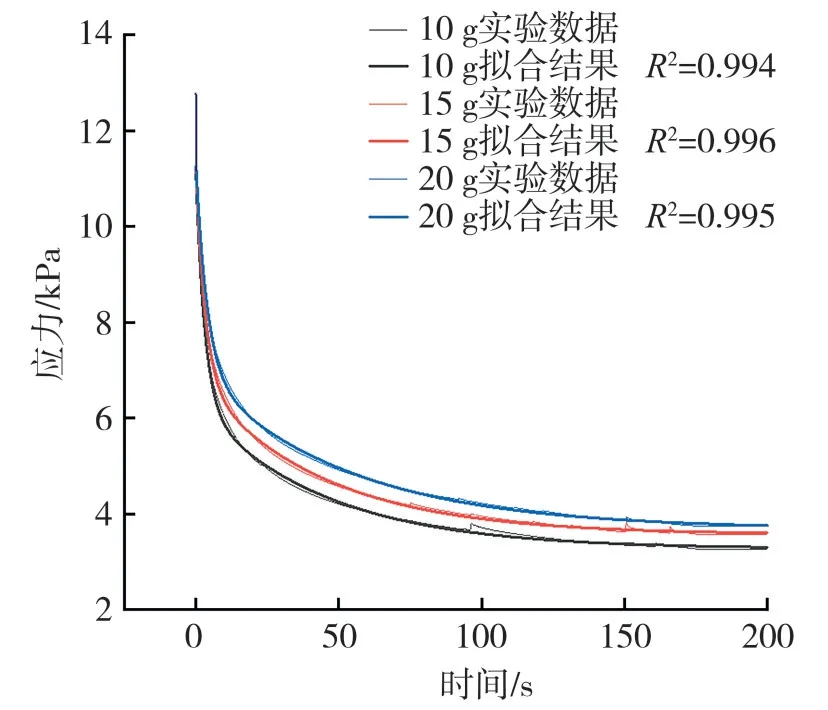
图6 不同样品量下五元件广义Maxwell模型拟合曲线Fig.6 Fitting curves of the five-element generalized Maxwell model under different sample amounts

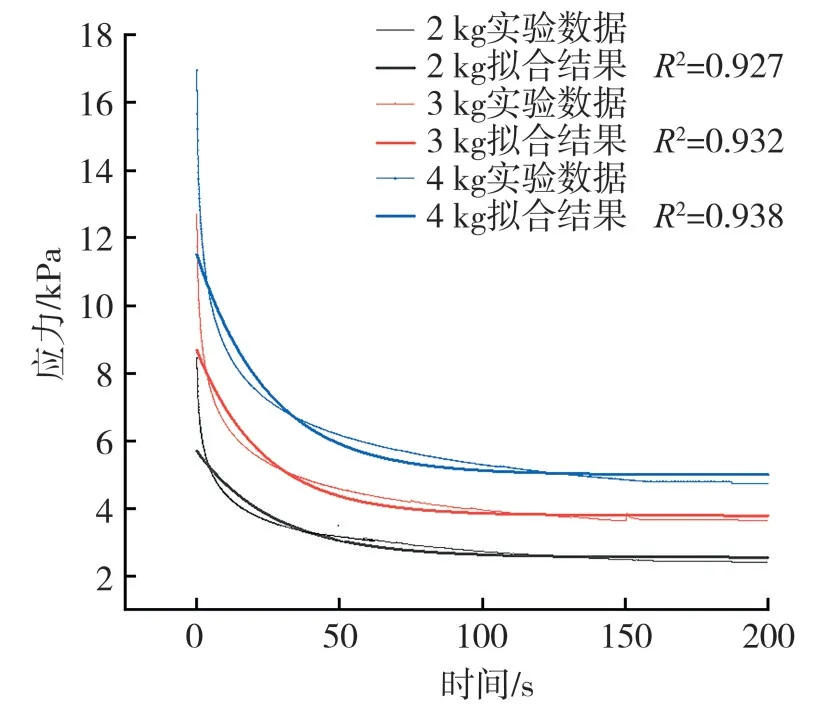
图7 不同压缩载荷下三元件拟合曲线Fig.7 Fitting curves of the three-element generalized Maxwell model under different compression loads

图8 不同压缩载荷下五元件拟合曲线Fig.8 Fitting curves of the five-element generalized Maxwell model under different compression loads

2.2.2 重复性验证

图9 为应力松弛重复性实验曲线图，由图可知6次平行实验的应力松弛曲线基本重合，由此可以证明该方法所得数据可信。采用五元件广义Maxwell模型本构方程求解烟丝应力松弛过程中的流变学参数，用变异系数对6次平行实验进行重复性评价，五元件广义Maxwell 模型对应的各流变参数的变异系数如表1所示。由表中数据可知，各参数的变异系数均小于5.0%，最大为3.0%，说明所建立的方法重复性较好，且利用五元件广义Maxwell 模型解释烟丝的应力松弛行为可靠。

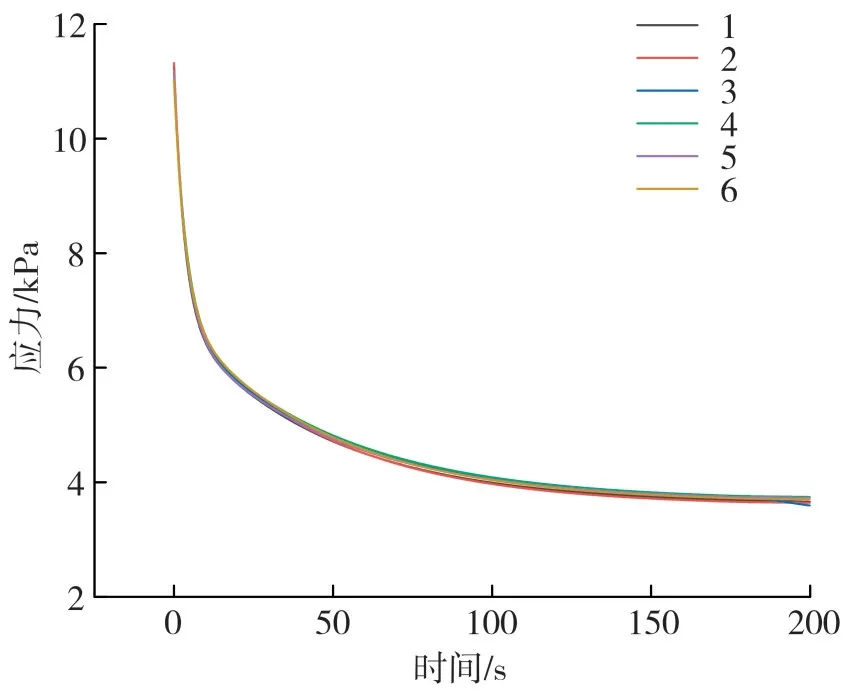
图9 应力松弛重复性试验曲线Fig.9 Repeatability curve of stress relaxation test

2.3 样品量对模型及参数的影响

当保持压缩载荷不变，样品量分别为10、15、20 g时，得到不同样品量下烟丝的应力松弛曲线，如图10所示。流变学参数如表2所示。分析发现：样品量的大小不影响烟丝的应力松弛规律，但是影响应力松弛过程中流变学参数值的大小。随着样品量的增加，平衡应力和平衡弹性模量增大，说明样品量越大最终保留在并联弹簧中的残余应力越大。不同样品量条件下，T1的变化范围为3.20~4.13 s，0~T1时间段内弹性恢复力快速衰减（对应图4的CD段）；T2的变化范围为46.22~55.72 s，T1~T2时间段内弹性恢复力衰减速度变缓；在T2之后，应力衰减速度逐渐变缓直至平衡。

表2 不同样品量下五元件广义Maxwell模型拟合结果Tab.2 Fitting results of five-element generalized Maxwell model under different sample amounts

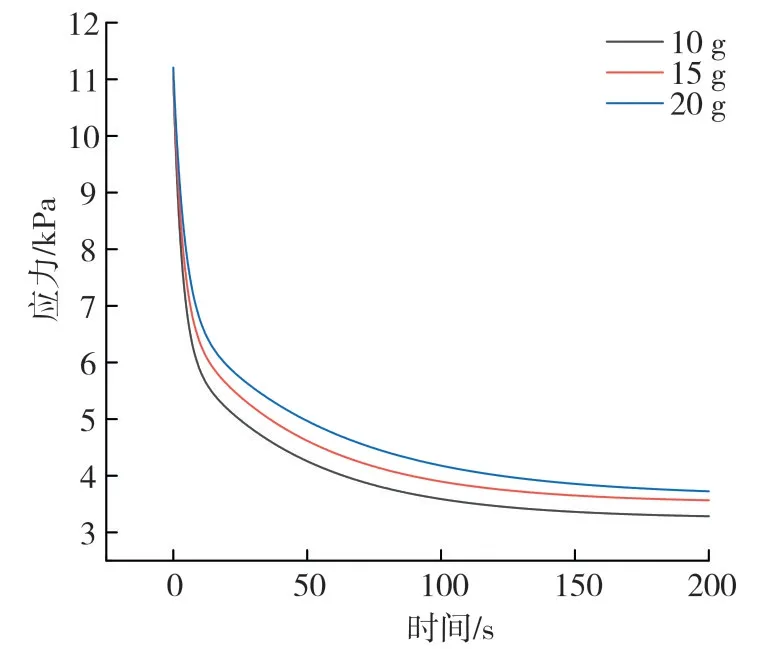
图10 不同样品量时烟丝的应力松弛拟合曲线Fig.10 Fitting curves of stress relaxation of cut tobacco under different sample amounts

由表2数据可知，各黏度系数随样品量的增加呈增大的趋势，弹性模量E1、E2变化规律不一致，两者的比值决定各Maxwell 元件的松弛时间。随着样品量的增加，T1、T2呈增大的趋势，对应的应力松弛时间比率α呈减小趋势，说明样品量越大应力松弛得越慢。

2.4 压缩载荷对模型及参数的影响

当保持样品量不变，压缩载荷分别为2、3、4 kg时，得到不同载荷下烟丝的应力松弛曲线和流变学参数，结果如表3和图11所示。分析发现：压缩载荷的大小不影响烟丝的应力松弛规律，但影响应力松弛过程中流变学参数值的大小。随着压缩载荷的增加，烟丝的初始弹性恢复力增大。相同时间内，压缩载荷决定烟丝的压缩密度，即压缩密度越大，起始弹性恢复力越大，平衡应力越大。与文献［15］中关于牧草应力松弛特性的研究得到的压缩密度与松弛应力之间的规律相同。

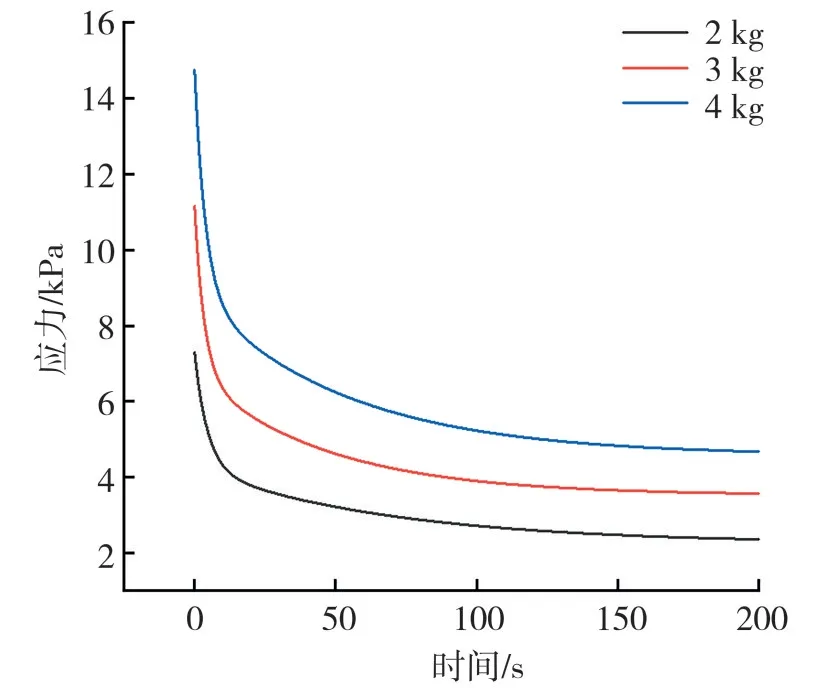
图11 不同压缩载荷下的应力松弛曲线Fig.11 Stress relaxation curves under different compression loads

不同载荷条件下，T1的变化范围为3.45~4.59 s，T1时间内弹性恢复力快速衰减；T2的变化范围为47.40~69.44 s，T1~T2时间段内弹性恢复力衰减速度变缓；在T2之后，应力衰减速度逐渐变缓直至平衡。由表3数据可知，各黏度系数和弹性模量都随载荷增大有增大的趋势，随着压缩载荷的增大，各Maxwell元件松弛时间先减小后增大，但压缩载荷越大，应力松弛时间比率α越大，即初始弹性恢复力越大（压缩载荷越大），应力松弛得越快。

3 结论

①通过对烟丝蠕变和应力松弛过程分析可知，烟丝压缩过程可以分为4个阶段：蠕变阶段、应力突降期、应力快速衰减期和应力缓慢衰减期。②基于农业物料压缩流变学理论，明确了烟丝应力松弛流变学模型为两个Maxwell 模型和一个平衡弹簧并联的五元件广义Maxwell 模型，并得到其本构方程。③考察了样品量和压缩载荷对烟丝应力松弛过程的影响。随着样品量和压缩载荷的增大，平衡应力呈增大趋势。样品量越大应力松弛时间比率α越小，压缩载荷越大α越大。