预应力混凝土连续刚构桥振动测试与动力特性分析
2023-08-01李冰徐行军
李冰,徐行军
(福建船政交通职业学院 土木工程学院,福建 福州 350007)
伴随我国经济得到迅猛发展,公路桥梁事业也突飞猛进。面对交通荷载与交通量剧增的新状态[1-3],很多旧桥的结构损伤问题逐渐显现出来,存着严重的安全隐患。而对桥梁损伤发现存在明显的滞后性、精准度不足情况,导致很多公路和城市桥梁都出现不同程度的病害,不仅让桥梁使用时间大大减少,对桥梁的安全健康运行造成威胁[4],同时过往人车的安全也无法得到保障[2,5-6]。因此,对我国在役桥梁进行检测评估具有重要的实现意义。
桥梁检测评估是桥梁维修的基础,为判断是否维修和保证维修质量提供重要参考,对于桥梁维修而言是至关重要的环节[2]。利用对预应力连续刚结构的振动测试,构建与桥梁目前实际吻合的有限元模型,利用实测值与计算值的对比分析来体现混凝土连续性刚结构动力特征。以更好地为桥梁健康评估与养护维修提供参考[7]。
1 测试大桥概况
测试桥梁采用1999 年通车的某省道混凝土T 型刚构桥,如图1。大桥设计荷载:按三列汽—26 设计,拖—100 验算,设计洪水频率:百年一遇,桥梁全长548 m,主孔跨径144 m,主桥上部为(107.5 m+110 m+144 m+110 m+107.5 m)4 墩5 孔混凝土连续刚构结构,下部结构为主墩、交界墩、桩基础,上部箱梁结构采用C 55 混凝土,主桥桥墩采用C 40 混凝土,箱梁为变截面单箱单室断面,箱梁顶面宽度9 m,箱梁底宽6 m;箱梁根部梁高7 m,跨中梁高为3 m,其间箱梁梁高变化采用1.8 次抛物线。主桥由跨中向两岸设置0.5 %的“人”字型纵坡,横向设2.0 %的双向横坡。桥面布置为1.5 m (人行道)+9 m (行车道) +1.5 m (人行道);江中两个深水基础为钢板桩围堰钻孔管柱桩基础;每个基础采用直径为155 cm 的旋制钢筋砼管柱16 根,江畔两个浅水基础为浅埋扩大基础。

图1 测试大桥Fig.1 Test the bridge
2 预应力连续梁桥振动测试
2.1 试验目的
测试桥梁结构的动力参数如自振频率、振幅、阻尼比及识别固有振型,了解大桥的基本动力特性;以动载测试获得的相关资料为依据构建桥梁目前实际情况的有限元模型;在模型修正基础上,正确评估桥梁的目前的使用状况,服务于桥梁的长期健康监测与状态评估。
2.2 试验仪器
动态测试仪器为INV 306 智能信号自动采集处理和分析系统:941-B 型水平向、垂直向速度传感器→INV-16 多功能抗混滤波放大器→306 G(LF)(32通道)东方科卡数据采集仪→COMPAQ 笔记本电脑→MACEC 动态数据处理软件包。
2.3 试验内容及过程
振动测试根据JTG/T J21-01—2015《公路桥梁荷载试验规程》的相关规定,因桥梁为已通车旧桥,动力试验荷载采用在随机的车辆、行人、自然风和地脉动的情况下,通过高灵敏度传感器及放大器获得各测点的振动信号,采集动力响应信息,再通过系统参数识别软件进行时频域分析,得到结构的频率、振型和阻尼比。根据结构振动特性并以有限元初步分析结果为指导,确定测试内容主要有:主桥水平向前5 阶自振频率及固有振型、主桥竖向前5 阶自振频率及固有振型、主桥纵向前2 阶自振频率及固有振型[8]。桥梁竖向和横桥水平向的测点及测站相同,各有5 个测站,每个测站9 个测点。采样时先用竖向加速度传感器采集数据,然后测站和测点不变,换成水平向加速度传感器。纵桥向振型和频率的测量分为2 个测站,每个测站9 个测点,各测点设备见图2(a~e),各个方向都设置一个固定参考点图2(f),位于该桥上游桥头。

图2 试验过程Fig.2 Test procedure
2.4 测点布置
利用测点获得桥梁各个方面的自振频率和振型。测试过程中,把各跨进行平均划分,一共分成八份,在桥的横向、纵向、竖向都设立测站,共计6 个。在主桥上的水平与垂直方向都分别设定测点四十五个,配有一个参考点;纵向有测点十八个,同样配一个参考点;主桥在这三个方面的测点合计171 个,测点布置如图3 所示。

图3 大桥测点布置图Fig.3 Layout of bridge
测试参数:横向和竖向频率都是100 Hz,滤波是100 Hz,采样时长是半小时[5]。纵向频率是400 Hz,滤波是400 Hz,采样时时长25 min。
3 预应力连续刚构桥动力特性分析
3.1 试验模态分析
目前,利用结构振动响应识别结构模态参数的工作模态分析方法有很多,包括基于频域的功率谱密度峰值法(PP)、频域分解法(FDD);以及基于时域的时序分析法(ARMA)、随机子空间法(SSI)和特征系统实现法(ERA)等[10]。为了保证识别的准确性,采用频域中的PP方法和时域中SSI 方法分别识别结构的模态参数,用峰值法可得到功率谱,由随机子空间方法可得到稳定图,使两种方法的识别结果互相验证。利用MACEC 软件进行试验数据分析,最后得出横、竖、纵三个方向的自振频率与振型情况[9]。对小模型而言,峰值法与子空间法均能计算出相应模态,具有较好准确性。对大模型而言,由于峰值法计算时所做假定为线性阻尼,而复杂大跨度结构的阻尼一般并非线性,峰值法适用性有所降低。而子空间法在逐阶稳定中能降低噪音影响,同时由于逐阶增长,该算法保证结构非线性阻尼的适用性,因此子空间法在大跨度结构计算中拟合度更为优异。
3.1.1 竖向自振频率和振型
利用峰值法可以获得竖向前5 阶频率,见图4。利用随机子空间法从测站获得数据稳定图5[10-12]。最后同时利用这两类方法可以获得竖向频率值[5],见表1。利用随机子空间方法,获得并处理由数据稳定图获得的数扰,即可以获得竖向的振型[7],如图10。
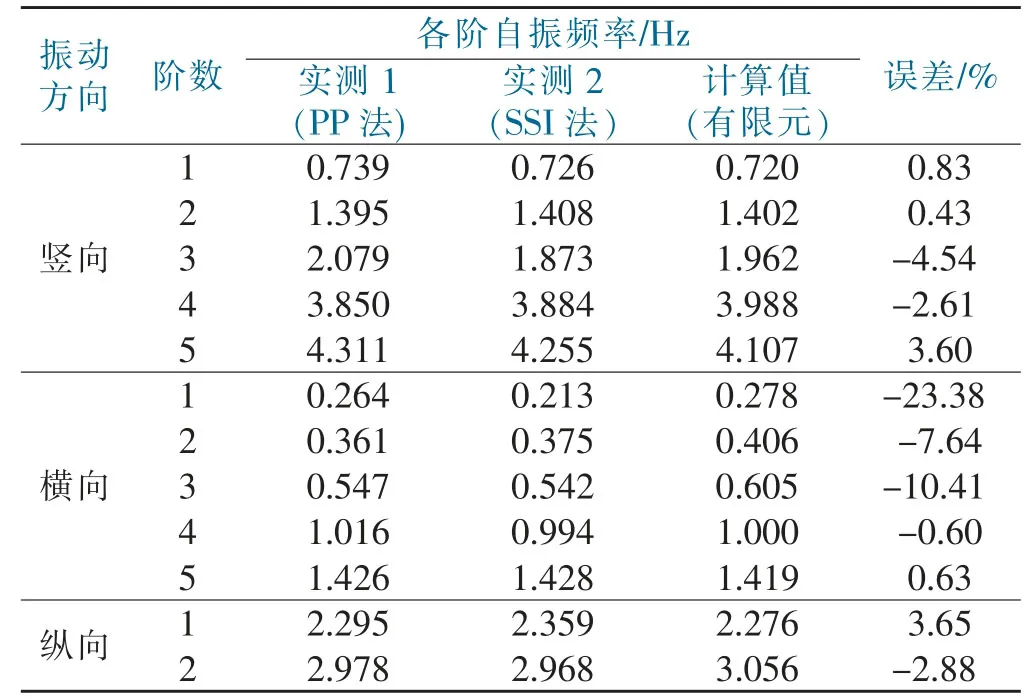
表1 各方向自振频率实测及模拟计算对比Tab.1 Measurement and simulation calculation comparison of spontaneous vibration frequency in each direction
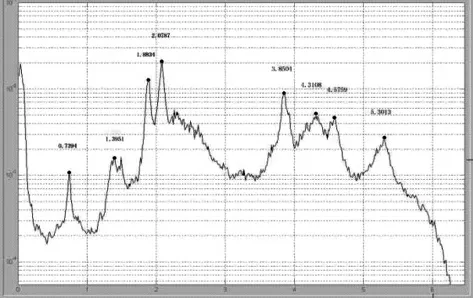
图4 竖向频率图(峰值法)Fig.4 Vertical frequency diagram (peak method)
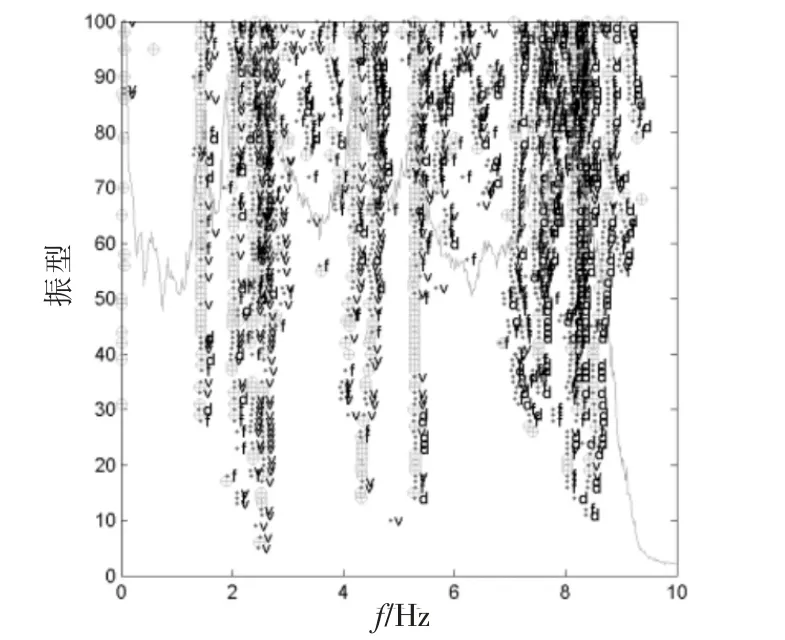
图5 竖向稳定图(测试数据)Fig.5 Vertical stability diagram (test data)
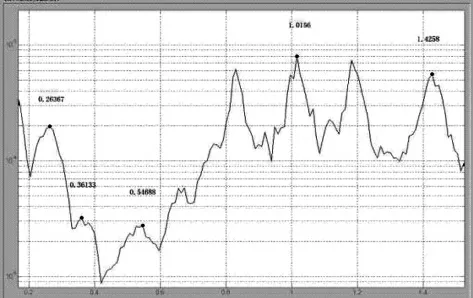
图6 横向频率图(峰值法)Fig.6 Horizontal frequency diagram (peak method)
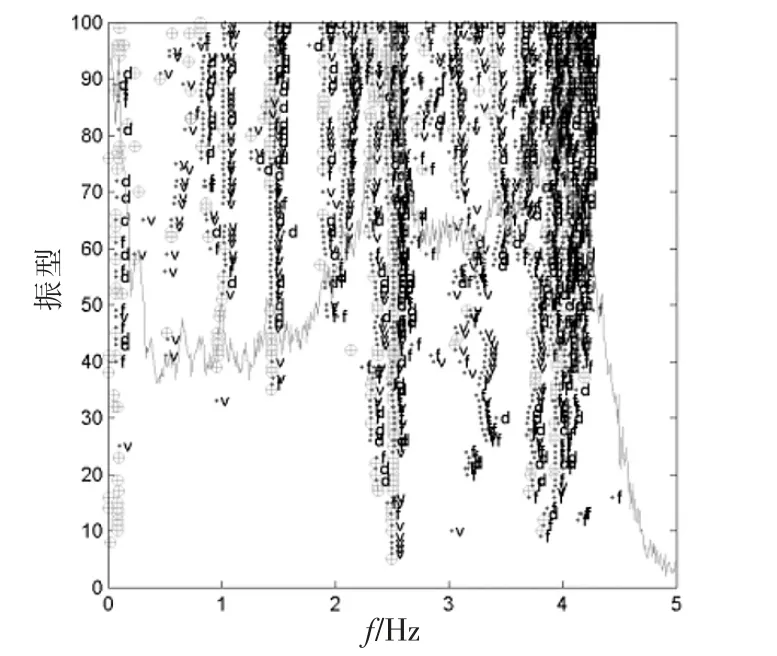
图7 横向稳定图(测试数据)Fig.7 lateral stability diagram (test data)
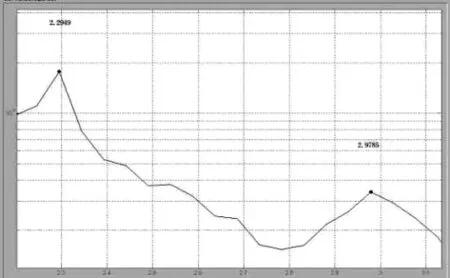
图8 纵向频率图(峰值法)Fig.8 Longitudinal frequency plot (peak method)

图9 纵向稳定图(测试数据)Fig.9 Longitudinal stability diagram (test data)
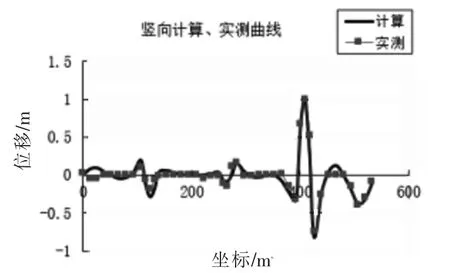
图10 竖桥向振型计算和实测比较Fig.10 Comparison of vertical bridge mode calculation and measurement
3.1.2 横向自振频率和振型
利用峰值法可以获得横向前5 阶频率图6。利用随机子空间法从测站获得数据稳定图7[10-12]。利用这两类方法可以获得横向频率值[5],见表1。利用随机子空间方法,获得并处理由数据稳定图获得的数扰,即可以获得横向的振型[7],如图11。
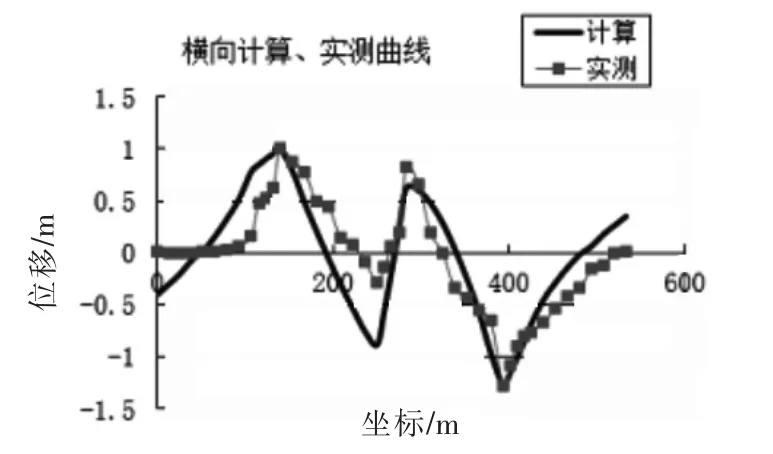
图11 横桥向振型计算和实测比较Fig.11 Comparison of transverse bridge mode calculation and measurement
3.1.3 纵桥向自振频率和振型
利用峰值法可以获得纵向前频率图8。利用随机子空间法可以从测站获得数据稳定图9[10-12]。利用这两类方法可以获得纵向频率值[5],见表1。利用随机子空间方法,可以获得前两阶的振型[7],如图12。
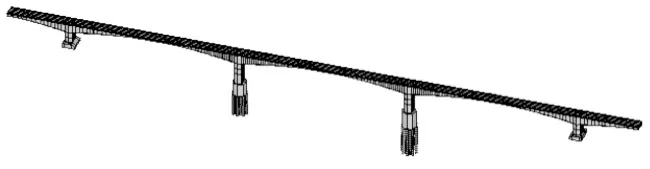
图12 大桥空间有限元模型Fig.12 Spatial finite element model of the bridge

图12 纵桥向振型计算和实测比较Fig.12 Comparison of longitudinal bridge mode calculation and measurement
3.2 有限元模型建立
以ANSYS 有限元分析软件为基础构建本桥的空间有限元模型[5],见图13。在该空间有限元模型中箱梁及挂梁都采用4 节点的板壳单元shell63,桥墩从箱梁底至承台采用8 节点的块体单元solid45,管桩采用管单元pipe16,桥面铺装层采用质量单元mass21 来控制桥梁两端伸缩缝的大小,同时利用弹簧单元combin14 模拟从横向与纵向两个方面进行控制[5]。1# 和4#墩承台底部固结。各管桩底部节点固结,在管桩至承台底范围内设置了一些弹簧单元combin14 来模拟桩土效应。该模型共有节点数3354 个,单元数4389个。主要参数设置为:桩土共同作用弹簧的刚度,k 取为2.375 M N/m;伸缩缝的弹簧的刚度,k 取为60 M N/m;混凝土弹性模量,以考虑混凝土弹模随时间的变化,进行动力计算时取设计值的1.08 倍。大桥主要材料参数见表2。
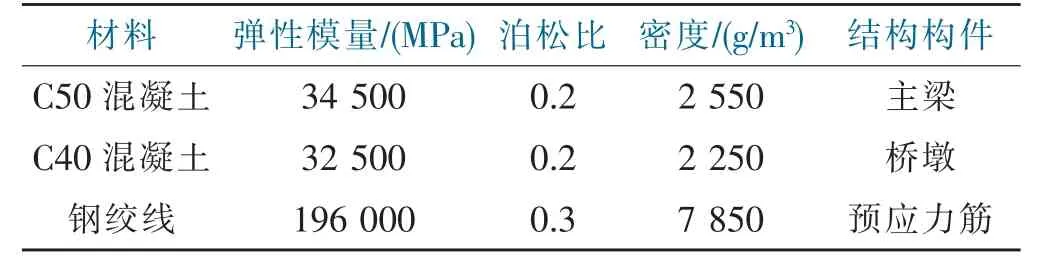
表2 材料参数表Tab.2 Material parameters table
3.3 实测数据与计算模拟自振频率对比分析
利用有限元与振动测试可以了解大桥基本动力特征[13-15],对比两组数据相应频率见表1。各个方向计算振型见图10~12。由表1 体现的数据可知,利用两种方法获得的频率基本相同。计算与实测频率整体契合,然而也有误差。导致误差出现的因素是有限元模型单元类型选择、材料参数等与实际有所区别[5]。
4 模态保证准则计算MAC 值的振型比较
在计算、实测振型的相关性方面,一般利用模态保证准则(MAC)实现,即:
式中:φa是计算模态振型向量,φe是实测模态振型向量。
如果模态完全相关,则假设两者没有任何关系,那么MAC 值趋向1,说明两者具有更强的相关性[16],测试大桥和实测模态的MAC 计算值见表3。

表3 计算MAC 值Tab.3 Calculate MAC values
根据图10~12 的第一跨的实测振型与有限元计算振型的结果,获得的MAC 值(见表2)大多数超过85%。(横向振型不包含在内),充分体现模态明显相关,计算振型和实测振型契合度高[2]。
5 结语
(1)环境振动测试最为突出的优点在于简单、可靠,保证交通正常运行,可以高效、准确地检测与评估桥梁的动力特性;它还可以应用于大跨径预应力混凝土T 构桥梁的基本动力特性的检测。
(2)桥梁动力特性的实测结果和有限元计算结果契合度高,充分体现出有限元模型和计算参数相对合理。
(3)频域识别方法的频谱图的峰值更加直观,然而这个值的选择依靠一定的业务能力;时域的随机子空间方法(SSI)可以得到稳定图,可以确保获得桥梁真实频率,同时还能体现较为契合的桥梁振型。
(4)测试桥梁仅对考虑该测试桥梁主梁构造、支座以及边界约束方式的影响。此次测试桥梁其纵向基频要大于竖向和横向基频,竖向基频大于横向基频,本桥的横向振动频率最小。
