基于多通道SQM 指标联合的矢量接收机多径干扰检测方法

贾琼琼，朱传胜

(中国民航大学 天津市智能信号与图像处理重点实验室,天津 300300)

0 引言

全球导航卫星系统(GNSS)能为其覆盖范围内的用户提供高精度的位置和时间信息，因此被广泛地应用于多个领域.矢量接收机通过充分利用各跟踪通道间信息共享能够达到通道间相互辅助的作用，因此在复杂环境下具有比传统标量接收机更优的性能.在城市峡谷等环境下，建筑物或其他障碍物会对卫星信号产生反射或散射，这些信号和直达信号一起进入接收机的现象称为多径传播.研究表明，多径干扰引起的伪距误差可以达到米级甚至百米级[1]，这足以影响系统的可靠性和定位精度.

尽管在复杂环境下，矢量接收机较之标量接收机具有性能优势，但是，多径仍然会对矢量接收机引入跟踪误差，导致其导航解偏离真实值.因此，如果能够及时检测到多径并加以处理，则有望降低多径对矢量接收机的影响，从而提高其在城市峡谷环境下的鲁棒性.

信号质量监测(SQM)技术最初是用来监测卫星异常的，它通过对接收机跟踪通道的相关值等输出进行监测以判断是否有干扰出现.SQM 已被广泛用于检测标量接收机中的多径干扰[2-8].文献[3-4]利用早码、即时码和晚码相关器的输出定义了对称和非对称Delta 和Ratio 指标，以监测卫星信号相关峰值中是否存在由多径引起的畸变.文献[5]利用多径干扰下跟踪环路相关曲线两侧不对称，提出了斜率不对称(SAM)指标来监测卫星信号是否受到多径影响.文献[6]通过定义Double Delta 指标研究了SQM 技术在GNSS 多径检测和缓解中的性能，提出了SQM 变化包络，并将其与相应的多径误差包络进行比较，以分析SQM 指标对GNSS 多径检测和缓解的敏感性和有效性.考虑到多径也会影响卫星信号的载波相位，Mubarak 等[7-8]提出了早-晚码相位(ELP)技术，利用早-晚相关器输出之间的相位差来检测多径干扰.

目前，基于SQM 实现矢量接收机多径干扰检测的研究还较少.文献[9]通过推导模型描述了矢量接收机下码和载波跟踪误差与多径延迟、相位和衰落频率的关系，并结合广义极大似然比检验和多相关器技术提出了一种多径检测方法，验证了其检测多径的有效性，但是没有与常用的SQM 指标进行对比分析多径干扰下的检测性能；文献[10]将早减晚相关器输出和C/N0估计器结合用作信号质量指标来检测多径，通过排除多径污染卫星提高了定位精度以及矢量跟踪性能.然而，现有的研究主要是基于矢量接收机各通道相关器输出进行检测，没有考虑不同SQM 指标在标量接收机和矢量接收机的区别.事实上，对于矢量接收机，多径干扰存在时不仅受干扰信号SQM指标出现异常，而且正常信号的指标值也会受到影响.

基于上述原因，本文提出基于多通道SQM 指标联合的矢量接收机多径干扰检测方法，该方法利用多径影响在矢量接收机各跟踪通道之间传递的特点，综合各通道的SQM 指标以使多径的影响得以积累，从而更易于发现多径干扰；在此基础上，再利用Double Delta 指标对实际接收到多径的通道加以识别.本文方法较之现有方法能更快速地发现多径，这有利于及时采取相应的措施对其进行处理，从而降低甚至消除多径对矢量接收机的影响.本文最后通过仿真实验验证了所提方法的有效性.

本文其他章节安排如下：第1 节给出了多径信号模型，并讨论了矢量跟踪结构和标量跟踪结构的区别，进而得到了多径对矢量接收机影响的特点；第2 节在分析常用SQM 指标在矢量接收机中多径监测特点的基础上，提出了基于多通道SQM 指标联合的矢量接收机多径检测方法；第3 节通过仿真实验验证了本文所提多径监测方法的有效性；第4 节进行了总结.

1 信号模型及问题描述

1.1 信号模型

本文以GPS L1 C/A 信号为例来分析多径的影响，所得结论可推广至其他卫星信号.假设当前时刻可见卫星数为n，其中第i颗卫星信号还存在一条反射路径的回波，此时包含多径干扰的中频信号可以表示为[10]

式中：Aj、τj、fD,j和φj分别为第j颗卫星信号的幅度、码时延、多普勒频率和载波相位；Cj(·) 为第j颗卫星信号的伪随机噪声码为第i颗卫星信号反射路径的幅度相对于直达信号幅度的衰减比和分别为该路径信号相对于直达路径的传输时延和载波相位，由于反射点一般在接收机附近，对信号多普勒频率的影响较小，因此可假设反射路径与直达路径的多普勒频率相同[11]；η (t) 为均值为零方差为的高斯白噪声.

GNSS 接收机码跟踪环路通常配置三个相关器，分别为早码(Early,E)、即时码(Prompt,P)和晚码(Late,L)相关器，其目的是通过比较三个相关器的输出来调整本地参考信号的码相位控制量.当接收信号为式(1)中的包含反射路径的多径传输时，三个相关器的输出分别为：

式中：IE、IP、IL分别为同相支路的早码，即时码和晚码相关值；QE、QP、QL分别为正交支路的早码，即时码和晚码相关值；Δ τj和Δφj分别为直达信号与本地信号之间的码相位差和载波相位差分别为多径信号与本地信号之间的码相位差和载波相位差；d为早码和晚码相关器之间的间隔；R(·) 为PRN码相关函数.

Tc为码宽.

对于不包含反射路径的卫星信号来说，其自相关函数的主峰值范围内可以看成对称三角形，如图1 中黑色线条所示.对于包含反射路径的卫星信号来说，其相关函数会发生畸变，如图1 中绿色线条所示，表示建设性多径发生时的相关函数.

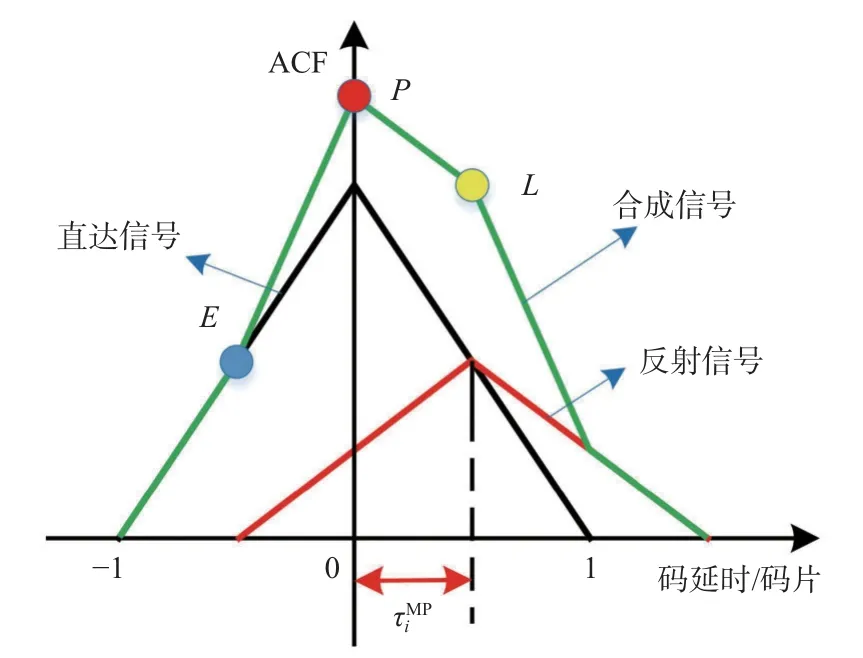
图1 多径干扰下的自相关函数

1.2 矢量接收机原理简介

传统的标量接收机各跟踪通道之间相互独立，如图2 所示，因此当多径干扰出现时，只有存在多径干扰的跟踪通道的相关函数会发生畸变，导致相关器的输出产生偏离，而对于不存在多径干扰的通道相关器的输出则不受影响.对于如图3 所示的基于矢量延迟锁定环(VDLL)的矢量接收机[12]来说，由于其各跟踪通道之间相互耦合，所有跟踪通道的本地信号码相位都是由反馈的导航解来控制的.由于导航解是各跟踪通道综合作用的结果，那么利用导航解来控制各通道本地信号的码相位就意味着各跟踪通道会受到其他跟踪通道的影响.为了讨论多径对矢量接收机的影响，下面首先简单介绍矢量接收机的工作原理.

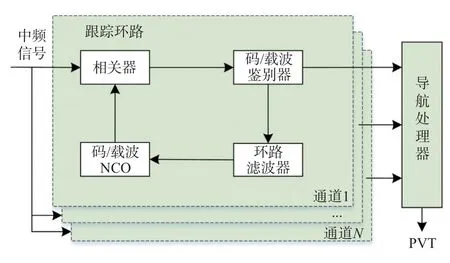
图2 标量接收机跟踪结构

图3 矢量接收机跟踪结构

定义X=[u,v,ctb,ctd]T为接收机的状态矢量，其中u=(ux,uy,uz)和v=(vx,vy,vz) 分别为接收机在地心地固坐标系(ECEF)中的三维位置和三维速度；c为光速；tb为接收机钟差；td为钟漂.定义接收机状态误差矢量为

式中：δu=(δux,δuy,δuz)、δv=(δvx,δvy,δvz) 分别为ECEF下的三维位置误差和三维速度误差；δtb和δtd分别为接收机的钟差误差和钟漂误差.

矢量接收机一般选用扩展卡尔曼滤波器(EKF)作为导航滤波器，其本质是求解下列问题：

式中：Fk,k+1为状态预测矩阵；wk为过程噪声矢量；Hk+1为观测矩阵；ηk为观测噪声矢量[13].矢量接收机的观测量Zk+1表示为

其中，前半部分为各通道的伪距误差观测量，其与码鉴别器输出 δ τj,k+1的关系可以表示为

式中：fCA为PRN 的码频率(对GPS L1 信号来说为1.023 MHz).对于本文的VDLL 矢量接收机来说，其伪距率误差通过下式计算：

式中：fd,j,k+1为第j颗卫星的多普勒频移频率；fL1为载波频率；vj,k+1为第j颗卫星的速度；aj,k+1=(ax,j,k+1,ay,j,k+1,az,j,k+1)为 接收机和第j颗卫星间的方向矢量.

EKF 求解式(7)分为两个步骤：第一步，根据当前时刻的导航解预测下一历元的接收机状态，即

式中：上标“-”为先验估计值；“+”为后验估计值.第一步为根据得到的状态预测值来更新本地参考信号的码相位，

式中，Δpj,k,k+1为 第j颗卫星在时间tk,k+1的位移矢量.

第二步为根据当前历元的观测量Zk+1求解状态误差的估计值并利用该值校正式(11)所得到的状态预测值，得到第k+1 个历元导航解[13]：

1.3 多径对矢量接收机的影响

假设第i颗卫星信号在第k个历元受到多径干扰，此时接收信号为式(1)所示.跟踪通道i的信号为直达和反射路径的和，致使该通道的相关器输出发生变化，进一步导致鉴别器输出发生偏离，最终导致该通道的伪距误差观测量出现偏差.同时，由于其他通道信号只有直达卫星信号，因此相应的伪距观测量不存在偏差.当第i个通道存在偏差的伪距误差观测量和其他通道正常的伪距误差观测量送入EKF 时，会导致误差状态的估计值出现偏差：

式中，偏差Xb来 自第i个跟踪通道伪距误差观测量.

此时利用式(13)进行导航解更新会导致导航解出现偏差：

假设导航解中速度估计不受影响，那么两个历元间接收机状态增量不存在偏差，则第k+1 个历元预测的码相位仍然存在偏差.当利用这些码相位生成本地参考信号时，则所有跟踪通道的本地参考信号都会偏离该颗卫星直达信号的码相位.对于第i颗卫星信号来说，接收到的信号仍然为直达信号和反射信号的合成信号，此时对应的相关函数如图4(a)所示，而对于其他卫星信号来说，接收信号中仅包含直达信号，因此相关函数仍然为正常的三角形，但是本地参考信号的码相位偏差会导致相关函数的中心位置发生偏移，如图4(b)所示.

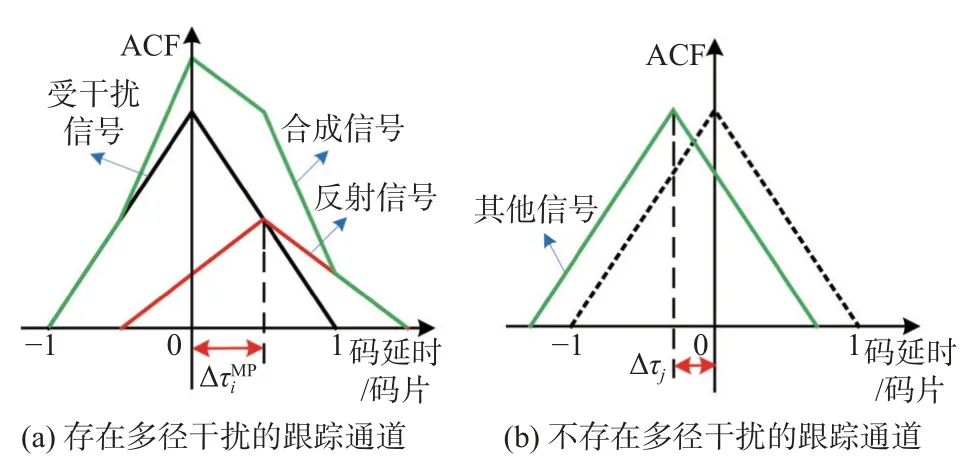
图4 多径干扰下矢量跟踪中不同跟踪通道信号相关函数

2 矢量接收机多径检测方法

本节首先给出了常用的SQM 指标，分析这些指标在标量接收机与矢量接收机中检测多径干扰的有效性，在此基础上结合矢量接收机跟踪误差在各通道之间的传递特性，提出了基于多通道SQM 指标联合的矢量接收机多径检测方法.

2.1 常用SQM 指标

表1 给出了常用的SQM 指标.其中Delta 指标是利用早码和晚码之间的差异来检测相关函数的不对称性.在没有干扰的情况下，指标值通常为零.然而，当存在多径时，相关函数曲线会发生畸变，峰值两侧不再对称，如图1 所示.此时，Delta 指标将偏离零值.Ratio 指标与Delta 指标类似，它是通过对一对早-晚相关器的两个值求和来检测多径干扰出现时相关函数的失真，主要用于检测相关峰出现异常尖锐或平坦的情况.在本文中，Ratio 和Delta 指标中早晚相关器的间隔d设置为0.1 码片.Double Delta 指标是基于由即时相关器归一化的两对早-晚相关器之间的差来定义的，被广泛应用于GNSS 失真检测[6,14].一般，两对早-晚相关器的间隔分别为0.2 和1 码片[6].ELP指标利用早-晚相关器输出之间的相位差来检测干扰，包含同相分量和正交分量，已被证实可用于检测多径干扰.多径存在时相关峰两侧会出现失真，通常延迟的反射信号会使相关曲线的右侧更加明显，因此Slope 指标一般由晚码相关器组成[15].Slope 指标中的IL1和IL2对应的相关器间隔分别设置为d1=1.8 和d2=0.2码片，无干扰时Slope 指标的均值为-1.

表1 常用的SQM 指标

上述的5 个指标最初是用于跟踪标量中监测卫星信号的质量，也被广泛应用于检测标量接收机中的多径或欺骗式干扰.表1 中最后一个指标是文献[16]针对矢量跟踪下欺骗干扰检测问题提出的.在本文中，ELP[8]和文献[16]指标中选用的早-晚相关器间隔均为1 个码片.

通过1.3 节的分析可知，对于包含多径干扰的跟踪通道来说，相关函数会发生畸变，这会导致Ratio和Delta 指标值偏离正常情况对应的值.矢量接收机各跟踪通道之间的耦合会导致不含多径干扰的跟踪通道的本地参考的码相位偏离真实接收信号的码相位，这也会导致这些跟踪通道的Ratio 和Delta 指标值偏离正常值.图5(a)和图5(b)分别给出了多径干扰出现时，各跟踪通道的Ratio 和Delta 指标值，其中只有2 号卫星受到多径干扰.可以看出，在10～20 s多径干扰持续期间，矢量接收机所有跟踪通道的指标值均偏离正常无多径时的均值.

图5 多径干扰下Ratio 和Delta 指标变化

而对于Double Delta 指标，它被定义为两对早-晚相关器之间的差异[2]，当相关峰两侧斜率不相等时Double Delta 指标就会发生变化，结合1.3 节的分析可知，只有包含多径干扰的跟踪通道Double Delta 指标会出现异常，而对于其他跟踪通道，由于相关函数不发生畸变，所以相应的Double Delta 指标不会发生异常变化.Slope 指标和文献[16]给出的指标与Double Delta 指标的检测原理类似，均利用正常信号相关峰值两侧斜率不变的特点来检测干扰，因此也只有包含多径干扰的通道指标值会发生变化.本文研究的矢量跟踪是VDLL，载波跟踪是传统的锁相环，而ELP 指标是利用直达信号和多径信号之间的载波相位差来检测多径，因此ELP 适用于本文矢量跟踪结构下的多径干扰检测.综上，上述4 个指标适用于本文研究的矢量接收机结构，能够不受矢量跟踪中误差传递的影响，检测出受到多径干扰的信号.图6 给出了上述2 号卫星在10～20 s 期间存在多径干扰时，根据矢量接收机跟踪环路输出的参数计算出的上述4 个SQM 指标.从图6 可以看出，仅有存在多径干扰的2 号卫星跟踪通道得到的上述4 个SQM 指标值出现异常，而其余跟踪通道的指标值不发生变化，这与上述理论分析结论一致.

图6 多径干扰下Double Delta、ELP、Slope 和文献[16]提出的指标变化

2.2 本文提出的多径检测方法

从2.1 节的分析可知，矢量接收机各跟踪通道之间的耦合导致多径干扰出现期间，所有跟踪通道的Ratio 和Delta 指标出现异常.因此，可以利用矢量跟踪结构这一特性来检测多径干扰，基于此本文提出了联合所有跟踪通道的SQM 指标检测多径干扰的方法，为此，构建如下联合指标：

式中：(·) 为 不同类型的信号质量监测指标；mξ,(·)为第ξ个跟踪通道的指标值.

多通道联合的核心思想是联合所有通道的异常来突出多径所引起的SQM 指标值的变化，因此能够在干扰出现时及时发现异常.根据文献[17]，在干扰不存在的情况下，Ratio 和Delta 指标均可以看作服从高斯分布.在对Ratio 和Delta 指标求其相应的联合指标时，因为Ratio 指标的均值大于0，取绝对值后的Ratio 指标 |mRatio| 依然服从高斯分布.而Delta 指标的均值等于0，所以取绝对值后的Delta 指标 |mDelta| 服从半正态分布[18].令x=|mDelta|，则 |mDelta| 的概率密度函数由下式给出：

式 中：σx表示 |mDelta| 方差；|mDelta| 均值ux=图7说明了在没有多径干扰的情况下，推导的理论概率密度函数曲线与直方图之间的比较.通过运行 4 ×104次模拟试验获得直方图.可以看到，SQM 指标绝对值|mRatio|和 |mDelta| 的理论概率密度函数曲线与直方图是一致的.

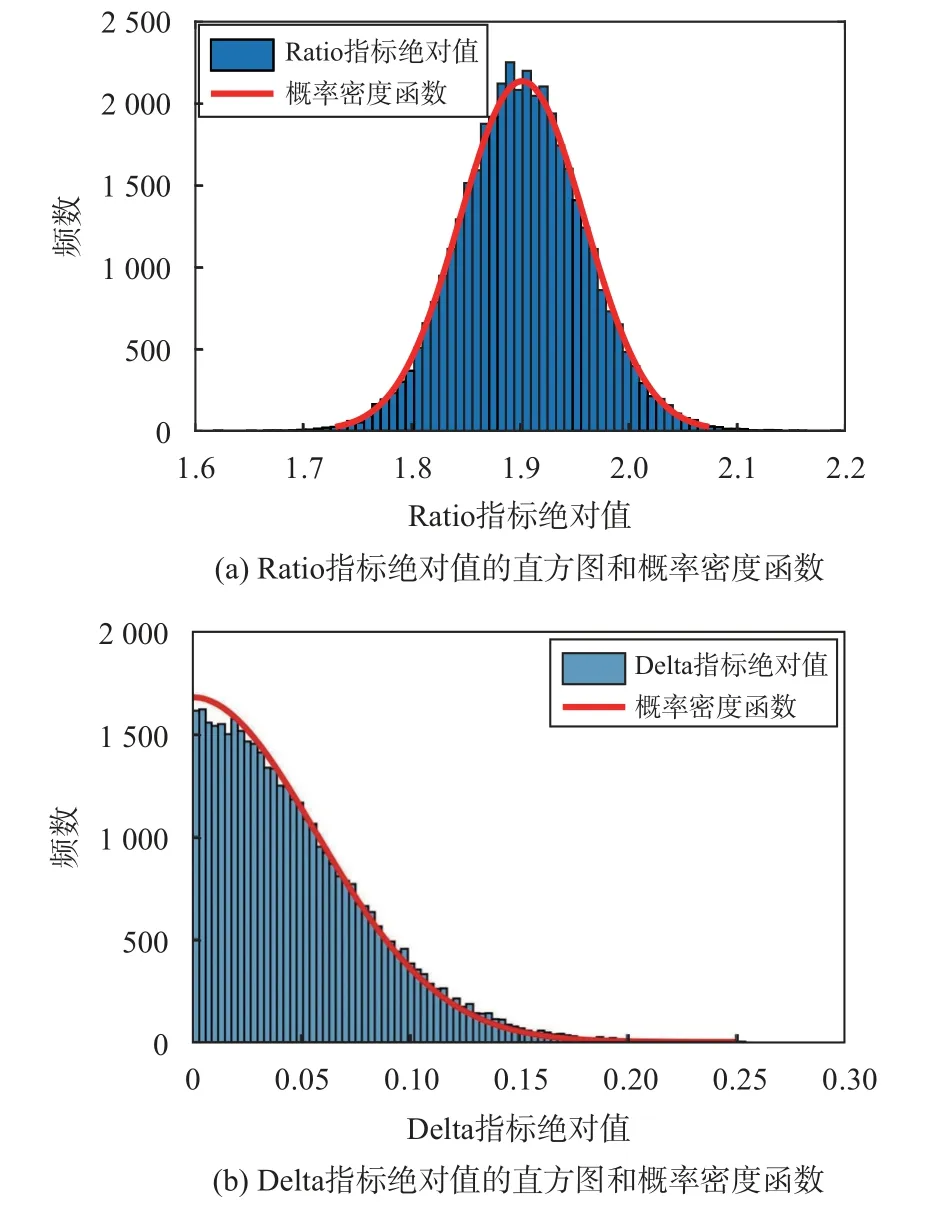
图7 Ratio 指标和Delta 指标取绝对值后的直方图以及理论概率密度函数曲线

多径干扰检测可以看作一个二元检测问题，定义二元检测模型如下：

式中：H0表示不存在多径干扰；H1表示存在多径干扰；Tu和Tl分别为上检测门限和下检测门限.通过计算虚警概率和检测概率来分析多径干扰检测性能，虚警概率Pfa表示为

式中：虚警概率Pfa为不存在干扰时超过给定门限的联合指标数与样本总量Mclear之间的比率；检测概率Pd为多径干扰存在时超过给定门限的联合指标数与样本总量MMP之间的比率.通过预设虚警率，根据式(21)可以计算对应的检测门限，然后由式(22)得到多径干扰下指标的检测率.

然而，多通道联合的方式却不能识别出存在多径干扰的跟踪通道，因此，本文将进一步利用Double Delta 指标来判断干扰所在的跟踪通道，这是基于上2.1 节所得到的该指标只有在存在多径干扰的跟踪通道时会出现异常.图8 给出了本文所提多径检测方法的流程图，具体步骤可以描述如下：

图8 本文方法流程图

步骤1：根据各跟踪通道的相关器输出，分别计算出其对应的SQM 指标值(这里为Ratio 或Delta).

步骤2：根据步骤1 所得到的各跟踪通道的SQM 指标值，利用式(17)计算对应的联合检验统计量mJ(·).

步骤3：判断mJ(·)是否超过检测门限，如果超过门限，则判定有信号受到多径干扰，进入下一步识别受干扰信号；否则，判定信号间不存在多径.

步骤4：计算各跟踪通道的Double Delta 指标mDD，当mDD超过检测门限，则表明该跟踪通道信号受到多径干扰；否则不存在多径干扰，从而识别出多径干扰所在的跟踪通道.

3 实验分析

在本节中，我们通过分析单个指标和多通道联合指标来评估多径干扰检测性能.针对GPS L1 波段信号进行数据仿真，将所提的检测方法分别应用在矢量跟踪上，在多径干扰的环境下进行检测实验和性能评估.仿真实验的相关参数设置如表2 所示，其中2 号卫星信号受到多径干扰，其他信号无干扰，干扰时间为10～20 s.

表2 仿真实验参数设置

首先对表1 中总结的常用SQM 指标进行多径干扰下的性能分析.为了得到准确的检测概率，采用恒虚警率方法进行处理.设定虚警概率为10%，通过式(21)计算多径检测的阈值，检测概率是通过计算每500 ms 超过门限的样本数除以该时间间隔内的样本总数来获得的，根据式(22)检测概率的计算方法可以得到所求指标在整个数据时间内的检测率，如图9 所示.可以看出在没有多径干扰的前10 s，所有指标的检测率都在10%左右，符合虚警率为10%的设定；在10～20 s 多径干扰期间，所有指标的检测率都出现了变化，大多数指标的检测率在50%上下波动，而ELP 的检测率在40%以下低于其他指标.图10显示了图9 中所有指标的接受者操作特征曲线(ROC)，ROC 曲线上的点越靠近左上角，检测的准确性就越高.检测窗口为10 s，即多径干扰存在的10～20 s.可以看到，随着虚警率的提高所有指标的检测率都发生相应的变化，Ratio、Delta、Double Delta 和Slope 这4 个SQM 指标的检测性能比较接近.

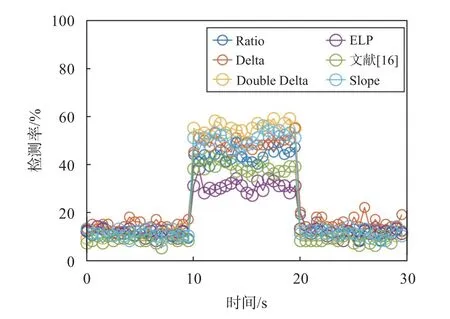
图9 SQM 指标检测率随时间变化趋势

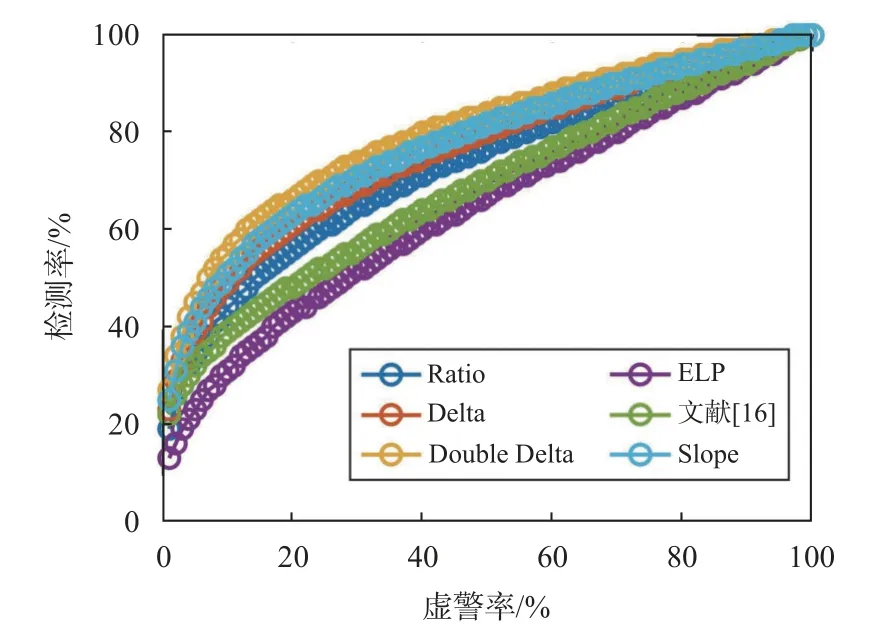
图10 SQM 指标检测率随虚警率变化趋势

为了进一步分析多径干扰下不同SQM 指标的检测性能，分别研究了不同指标检测率随码延时和多径相对幅度变化趋势，虚警率同样设置为10%.图11给出了多径相对幅度为0.3 时，指标检测率随码延时变化结果.当码延时增大时，只有Slope 指标的检测率出现提高；并且当码延时大于0.5 码片时，Slope 指标的检测率明显高于其他指标.图12 给出了多径码延时为0.3 码片时，指标检测率随多径相对幅度的变化结果.可以看到，随着相对幅度的增大，所有指标的检测率都出现不同程度的提高，Double Delta 指标检测率提升最为明显，当相对幅度为0.8 时，Double Delta 指标的检测率能达到98%.

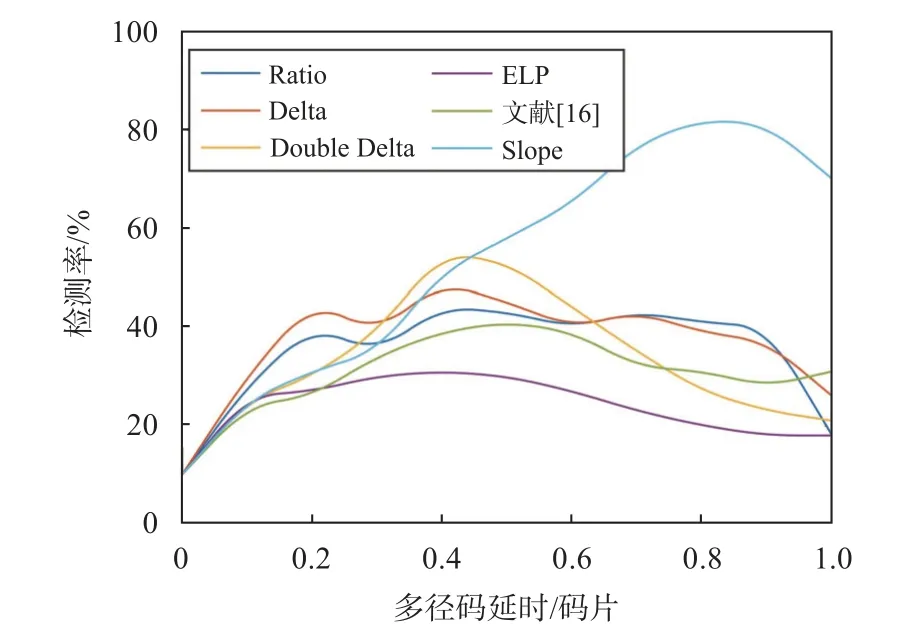
图11 SQM 指标检测率随多径码延时变化趋势

图12 SQM 指标检测率随多径相对幅度变化趋势

接下来分析联合指标的多径干扰检测性能.对Ratio 和Delta 指标进行多通道联合，并与Double Delta、Slope 指标进行对比分析.图13 给出了多通道联合指标检测率随时间变化趋势.可以看到，联合后的Ratio 和Delta 指标与没有经过联合的Ratio 和Delta 指标相比，检测率都有不同程度的提高.其中联合Ratio 指标检测率提升得更加明显，检测率可达到76%，且高于其他指标.进一步分析多通道联合指标和其他指标检测率随虚警率变化的结果，如图14 所示.显然，联合Ratio 指标的检测性能优于其他指标，而联合Delta 指标与Delta 指标相比，检测性能有一定的提升.

图13 多通道联合指标检测率随时间变化趋势

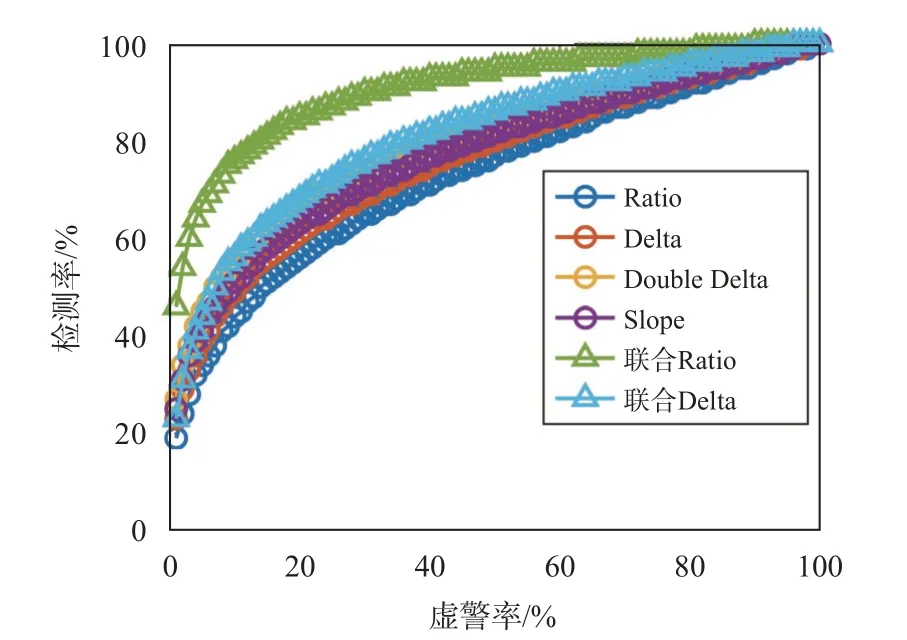
图14 多通道联合指标检测率随虚警率变化趋势

同样地，在多径干扰存在的时间内，分析多径码延时和相对幅度对多通道联合指标检测性能的影响.图15 为多通道联合指标检测率随多径码延时变化的结果.可以看出：联合Ratio 指标在码延时为0.3～0.6码片时，检测率高于其他指标；当码延时为0.4 码片时，联合Ratio 指标检测率可达到76%.图16 显示了多通道联合指标检测率随多径相对幅度变化的结果，当多径相对幅度小于0.5 时，联合Ratio 指标的检测性能优于其他指标.

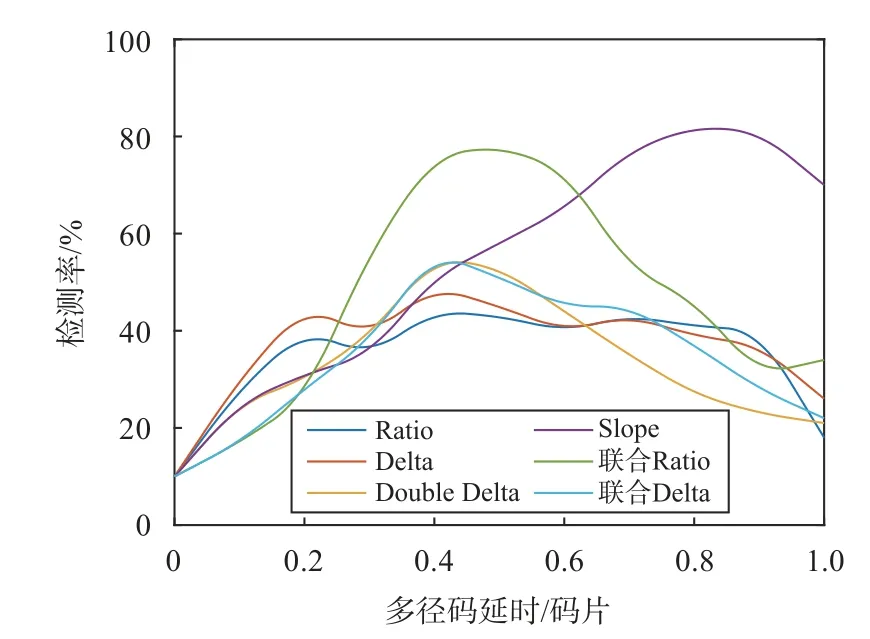
图15 多通道联合指标检测率随码延时变化趋势

图16 多通道联合指标检测率随多径相对幅度变化趋势

多通道联合指标检测到多径干扰后，通过二次检测识别出受干扰的信号，采用2.2 节结合Double Delta 指标的方法进行干扰识别.根据图8 对联合Ratio 指标进行二次检测，将二次检测后检测率随虚警率变化的结果与另外四个指标进行比较，如图17所示.可以看出，经过二次检测后的联合Ratio 检测性能优于文献[16]和ELP 指标.

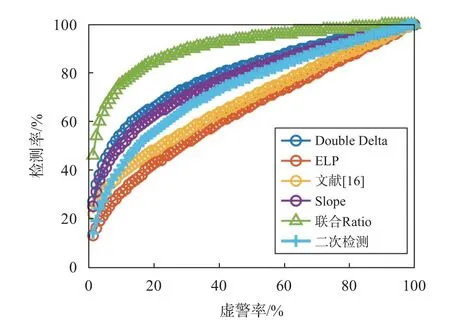
图17 二次检测后多通道联合指标检测率随虚警率变化趋势

4 结束语

本文研究了矢量接收机中的多径干扰检测问题，结合矢量接收机存在误差会在跟踪通道间传递的特性，提出了基于多通道SQM 指标联合的矢量接收机多径检测方法.通过仿真实验验证了较之单一的Ratio 和Delta 指标，本文所提出的联合Ratio 和联合Delta 指标多径干扰检测性能均有不同程度的提升，其中联合Ratio 指标在多径相对幅度小于0.5 且码延时为0.3～0.6 码片时，检测性能优于其他指标.