不同截止高度角下天线阵列RTK 定位分析

王超，刘长建，肖国锐，孙爽，孟欣

(信息工程大学地理空间信息学院,郑州 450001)

0 引言

实时动态(RTK)是一种利用载波相位观测值实现高精度定位的技术之一，载波相位整周模糊度正确固定是RTK 达到厘米级甚至毫米级定位的关键[1].为解决模糊度固定问题，基于整数最小二乘理论的算法是当前模糊度解算方法中关注最多的，这类方法中比较有代表性的有最小二乘模糊度降相关平差(LAMBDA)[2]、三频载波模糊度解(TCAR)[3]、最优GPS 模糊度估计(OMEGA)等[4].同时模糊度固定还取决于全球卫星导航系统(GNSS)的模型强度及观测值精度，相同观测精度下模型强度越强模糊度就越容易固定[5-6].为增强GNSS 模型强度，一些学者使用多频、多系统组合的GNSS 定位方法，结果表明：双频、三频组合的模糊度固定率高于单频[7-10]，多系统组合能够改善卫星空间几何结构，提高定位精度[11-13].另外基于多接收机组合的方法已被广泛使用，例如多元约束的姿态确定[14-16]、多动态参考差分增强定位[17]、天线阵列辅助精密单点定位(PPP)等[18].

研究表明多台接收机组成的天线阵列能够提高RTK 模糊度固定成功率与可靠性[19]，但目前对天线阵列RTK 的研究较少，文献[6，19]主要对天线阵列RTK 的模糊度固定进行分析，对其定位性能分析较少，对不同截止高度角下的天线阵列RTK 定位研究不足.设置不同截止高度角在一定程度上能够模拟树木、建筑遮挡卫星信号的情况，所以不同截止高度角下的天线阵列RTK 定位性能分析具有一定的研究和应用价值.

为此，本文对比分析了天线阵列RTK 与RTK 的数学模型，研究了20°～50°截止高度角下GPS 单系统、BDS 单系统以及GPS+BDS 的天线阵列RTK 模糊度固定与定位性能，并与RTK 计算结果进行比较，验证了天线阵列RTK 模型的可行性，并提高了RTK 在大截止高度角下的适用性.

1 天线阵列RTK 模型

1.1 观测模型

假设原始伪距、载波相位观测方程为

短基线背景下，电离层延迟与对流层延迟经双差处理后被极大削弱，因此忽略两者双差后的残余误差项.将r视为流动站接收机的标识，数字1 为参考站接收机标识，i、j为两颗可视卫星，在式(1)的基础上，得到双差观测方程为

假设s+1 颗 卫星在 第f个 频率上被同时观 测，根据文献[5]，基于式(3)可以得到RTK 的观测模型为

如图1 所示，由一台参考站接收机扩展到n台接收机时，一共能够构成n组双差观测方程，但由一组待求的参数向量变成了n组.参考文献[19]中，向量b为参考站1 和流动站r之间的基线向量，而本文基线向量b实际上为近似坐标与待求坐标间的改正值向量，因此每个参考站与流动站组成的观测方程中只需要选择相同的近似坐标展开就可以保证所有待求向量b相同.因为向量b具体含义不同，所以本文的天线阵列RTK 观测模型与文献[19]有所区别.

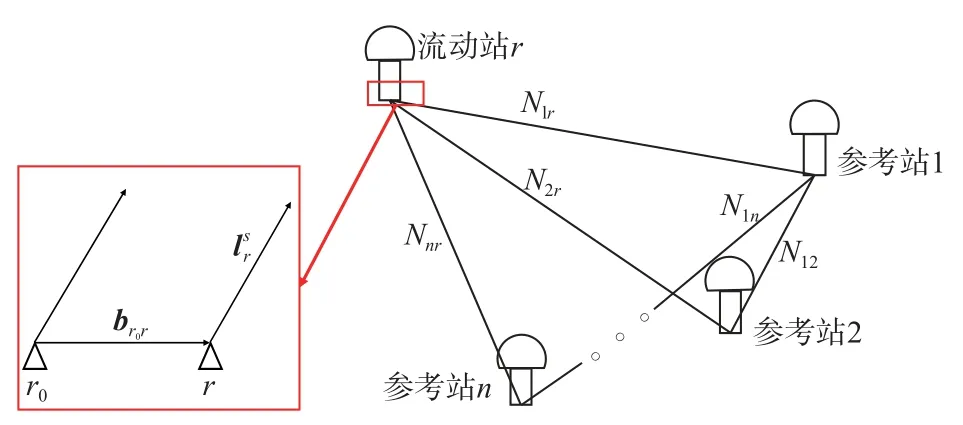
图1 天线阵列RTK 示意图

对于n组双差模糊度向量，有如下关系：

通过式(5)可以将其他的双差模糊度向量都转为一组待求的模糊度向量N1r.

将RTK 观测模型扩展为天线阵列RTK 观测模型，即

1.2 随机模型

根据参考文献[5]和文献[19]，直接给出RTK 的随机模型：

式中：ϕr、ϕ1,...,ϕn为载波相位星间单差OMC(已经减去近似点处的星地距离)；式中其他项与上文含义一致为n×(n+1)阶流动站与天线阵列间的差分矩阵，当n=1 时，DA变为单参考站与流动站间的差分矩阵.认为流动站和参考站1 ,...,n的星间单差观测值独立等精度，结合式(9)天线阵列RTK 的载波相位双差方程(伪距双差方程同理)，根据误差传播律，可以得到天线阵列RTK 的随机模型为：

1.3 与RTK 对比

首先对天线阵列RTK 和RTK 的数学模型进行对比.在观测模型方面，根据式(4)和式(6)，两种模型的形式具有一致性，区别在于天线阵列RTK 观测模型将更多观测值通过站间双差模糊度信息融合进行参数解算，增加双差方程的冗余度，提高了RTK 的模型强度.随机模型方面则根据观测模型的变化扩展了流动站和天线阵列间的差分矩阵.

本文使用LAMBDA 算法进行模糊度固定，需要先求出参数浮点解.天线阵列RTK 和RTK 通过与其对应的数学模型，根据最小二乘原理求得模糊度与基线向量的浮点解，篇幅限制未展示其推导过程.表1展示了天线阵列RTK 模型与RTK 模型的参数浮点解公式.

表1 天线阵列RTK 模型与RTK 模型参数浮点解公式

结合表1 中的公式可以推导出天线阵列RTK与RTK 这两种模型的参数浮点解的关系为

2 实验分析

2.1 实验描述

实验目的为分析不同截止高度角下的单GPS、单BDS 与GPS+BDS 双系统组合的天线阵列RTK定位性能，双系统采用松组合的形式，其中单系统和双系统都采用常见的频率组合，分别为L1+L2、B1I+B3I.实验使用澳大利亚科廷大学GNSS 中心的四台Trimble NETR9 接收机的观测数据进行定位实验，接收机天线为Trimble 59800，数据采样间隔为30 s.图2 为组成天线阵列的多台接收机分布情况，其中CUT00、CUTA0、CUTB0 组成天线阵列，CUTC0 视为流动站，其坐标待求；当用RTK 解算时，CUT00 为参考站，CUTC0 为流动站.分别使用天线阵列RTK模型与RTK 模型进行解算，采用LAMBDA 算法进行模糊度固定，比较模糊度固定后的坐标与已知坐标，当三维误差小于0.1 m 且通过ratio 检验则视为模糊度固定成功，其中ratio 检验阈值设为2.

图2 天线布局示意图

当截止高度角过大会导致一些历元的可用卫星数不能满足定位要求，本文对不同截止高度角下的解算率进行统计，解算率为满足定位要求的历元占所有历元的比例.卫星单系统至少有4 颗可用卫星，双系统组合不少于5 颗且每个卫星系统的可用卫星不少于2 颗才能获得单历元解.当高度角小于20°时，BDS 单系统和GPS 单系统的解算率都是100%，因此截止高度角小于20°的解算率情况就不予列出.从表2中看出，GPS 单系统在截止高度角45°时有效历元仅为37.7%，但BDS 和GPS+BDS 组合仍能保持较为连续的定位；当截止高度角为50°时，BDS 单系统的解算率为78.5%，有接近四分之一的历元解算失败，无法保持较连续定位.当截止高度角大于55°时，BDS 单系统只有12.5%的历元能满足定位需求，几乎完全丧失单独定位能力；GPS+BDS 组合系统在截止高度角为50°时，其解算率大于99%.GPS+BDS 组合系统在截止高度角为55°时，定位连续性锐减，截止高度角为60°时也完全丧失了连续定位的能力.

表2 不同截止高度角下各卫星系统的解算率 %

从图3 与表3 中可以看出，随着截止高度角的增加可视卫星数量减少，卫星空间几何结构变差，位置精度因子(PDOP)值变大.当截高度角为40°时，实验中GPS 单系统对应的PDOP 均值大于20，平均可视卫星数量为3.8 颗；而BDS 单系统在截止高度角为40°时，平均可视卫星数有6.1 颗，PDOP 均值为6.9，相对于GPS 单系统具有明显优势；GPS+BDS 双系统组合与单系统相比，组合系统的可视卫星数增加，卫星的几何结构更好，PDOP 均值在高度角为50°时为9.6，明显优于GPS 单系统和BDS 单系统.

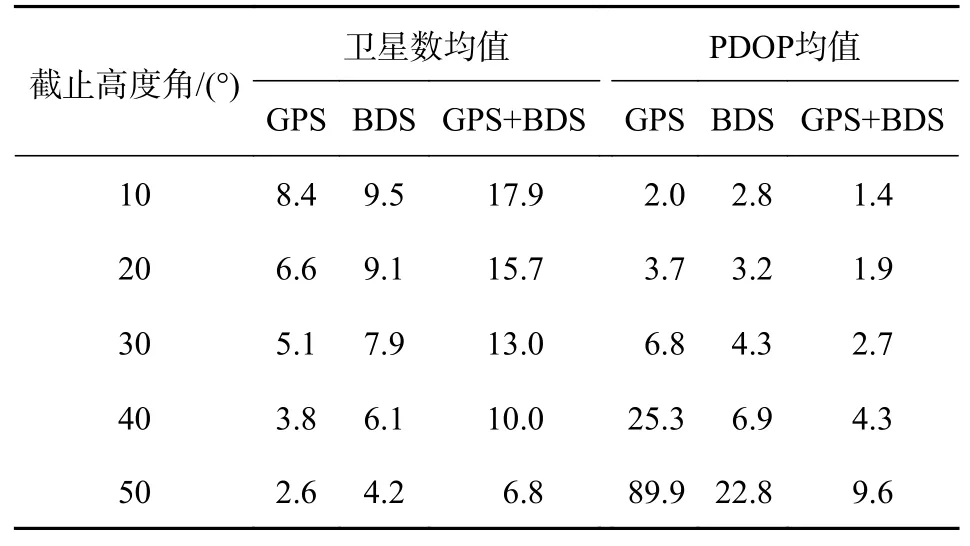
表3 不同截止高度角下各卫星系统PDOP 均值与可视卫星数均值

图3 不同截止高度角下PDOP 均值与可视卫星数均值

为具体分析天线阵列对于RTK 模型的增强，评估天线阵列RTK 的性能，分别使用天线阵列RTK 模型和RTK 模型计算BDS 单系统、GPS 单系统、BDS+GPS 三种情况下不同截止高度角的定位结果，并对两种模型所对应的模糊度衰减因子(ADOP)、模糊度固定成功率、浮点解、固定解进行分析.

2.2 模糊度固定分析

自举成功率Ps,IB计算简单，是整数最小二乘成功率的明显下限，能够用来分析整数最小二乘成功率.图4 中虚线代表的是天线阵列RTK 模型，实线是RTK 模型，可以看到，GPS 单系统在高度角大于20°时，两种模型计算的自举成功率就有较为明显的差距，而BDS 单系统在高度角大于40°、GPS+BDS在高度角大于45°时，自举成功率才有明显差距.结合表3 分析这可能是由于GPS 单系统在高度角大于20°时，模型强度受卫星数减少的影响，逐渐不能维持较高的模糊度自举成功率，同理基于BDS 单系统、GPS+BDS 的RTK 模型强度则分别在40°、45°时不能保证较高的自举成功率.以上这种情况意味着随着截止高度角的变大，RTK 模型在模糊度固定方面受到挑战，而天线阵列对模型的增强在一定程度上降低了模糊度固定的难度，在图4 中表现为在较高的截止高度角下，天线阵列RTK 的自举成功率高于RTK.

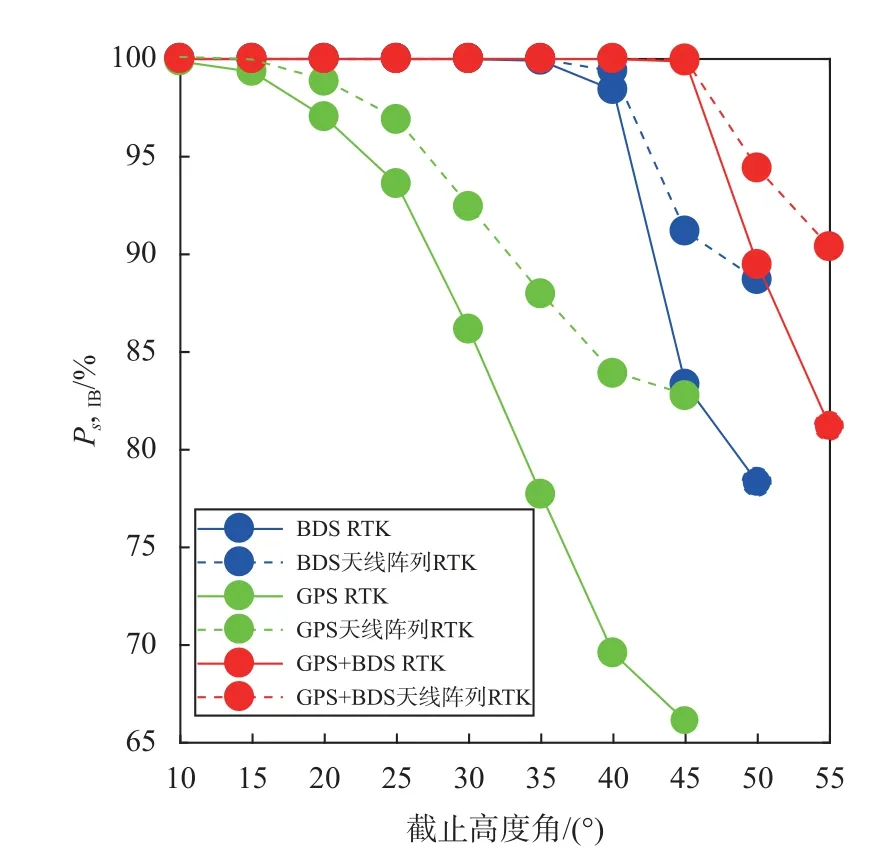
图4 天线阵列RTK 与RTK 在不同截止高度角下的平均自举成功率Ps,IB

表4 对两种模型不同截止高度角下各个卫星系统的模糊度固定成功率进行分析.当截止高度角为20°时，GPS 单系统的天线阵列RTK 模糊度固定成功率略高于RTK，与自举成功率分析的结果一致；当截止高度角为30°、35°、40°、45°时，相较于RTK，天线阵列RTK 模糊度固定成功率分别从90.4%、84.8%、78%、70.8%提高至93.5%、90.3%、84.7%、78.2%，最多提高了7.4%.BDS 单系统在截止高度角50°时，天线阵列RTK 提高最多，为8%.因为GPS+BDS 组合的模型强度高于GPS、BDS 单系统，能够较好地完成模糊度固定，所以在双系统组合定位时天线阵列对RTK 的增益较小，模糊度固定成功率在截止高度角55°时提高最多，为4.9%.

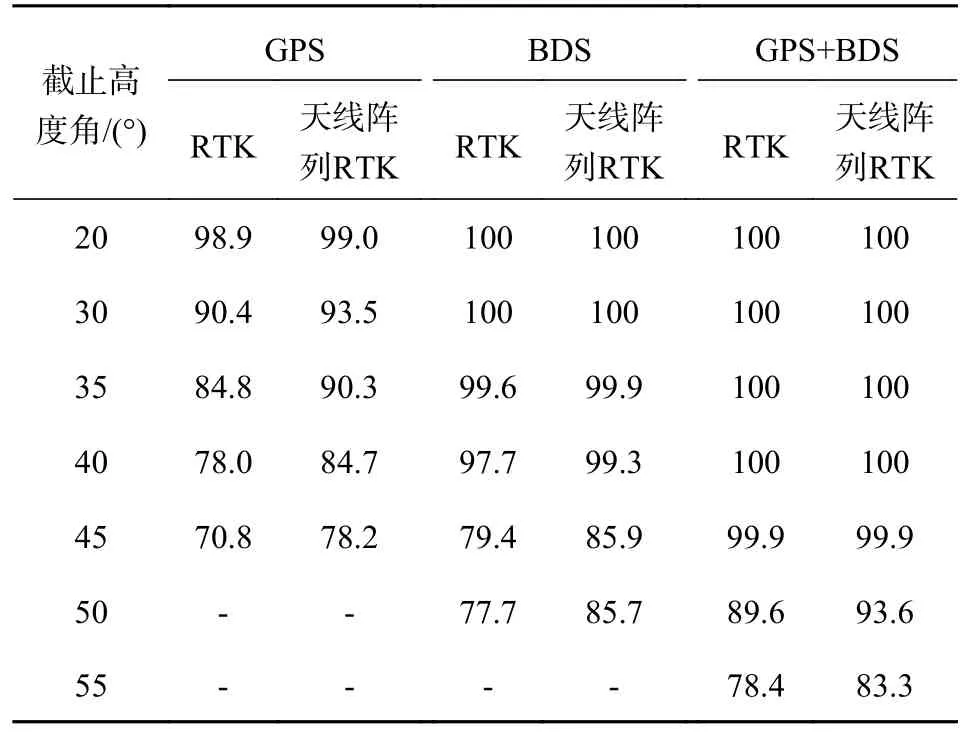
表4 天线阵列RTK 与RTK 在不同截止高度角下的模糊度固定成功率 %

结合图4、表3 和表4 发现，在低截止高度角可用卫星数量充足的情况下，例如高度角为20°时RTK 的模型强度能够保证较高的模糊度固定成功率，因此天线阵列RTK 的优势不明显.而由于截止高度角变大导致可视卫星减少，例如截止高度角由20°变为40°时，GPS 单系统平均可视卫星数由6.6 颗变为3.8 颗，卫星空间构型强度变弱，GPS 单系统的模糊度固定成功率迅速降低.不过由于天线阵列RTK 的模型强度高于RTK，即便其模型强度也随着卫星数减少而减弱，但模糊度固定成功率仍比RTK高6.7%.而在50°的大截止高度角时，天线阵列RTK 的模糊度固定成功率为93.6%，优于RTK 的89.6% 的模糊度固定率.表4 的结果表明，在低高度角GNSS 模型强度较高的情况下，天线阵列RTK 模型与RTK 模型的模糊度固定成功率没有太大差别，但在高截止高度角时，随着GNSS 模型强度的减弱，天线阵列RTK 模型的模糊度固定成功率明显优于RTK 模型.

接下来通过ADOP 值来解释天线阵列RTK 提高模糊度固定成功率的原因.ADOP 是一种能够衡量模糊度固定成功率且易于计算的标量因子，根据文献[5]，其定义为

式中：q是模糊度向量的维数；|·| 是行列式运算符.根据式(12)，模糊度浮点解精度越高ADOP 值越小，而同样条件下天线阵列RTK 模糊度浮点解精度高于RTK，所以其ADOP 值小于RTK.由于ADOP 值与模糊度搜索空间的体积对应相关，意味着天线阵列RTK 的模糊度搜索空间小于RTK，更有利于模糊度的搜索，并且ADOP 值等价于降相关后模糊度标准差的几何平均值，所以天线阵列RTK 的模糊度固定成功率高于RTK，不过天线阵列RTK 能够提高模糊度浮点解精度才是提高模糊度固定成功率的根本原因.

在图5 中，蓝色曲线和红色曲线分别表示的是天线阵列RTK 模型与RTK 模型计算的ADOP 值.图5(a)、(b)、(c)反映了基于两种模型计算的不同截止高度角下不同卫星系统所有历元的ADOP 均值，对比图5(a)和图5(b)发现，相同截止高度角下BDS的ADOP 均值都小于GPS，当截止高度角大于30°时，BDS 的ADOP 值明显小于GPS.结合表3 分析，可能由于BDS 的可视卫星数多于GPS，卫星几何结构更好.图5(d)是在截止高度角30°时，GPS 系统ADOP 值的时间序列，其更加直观地展示了天线阵列RTK 对ADOP 值的减小.

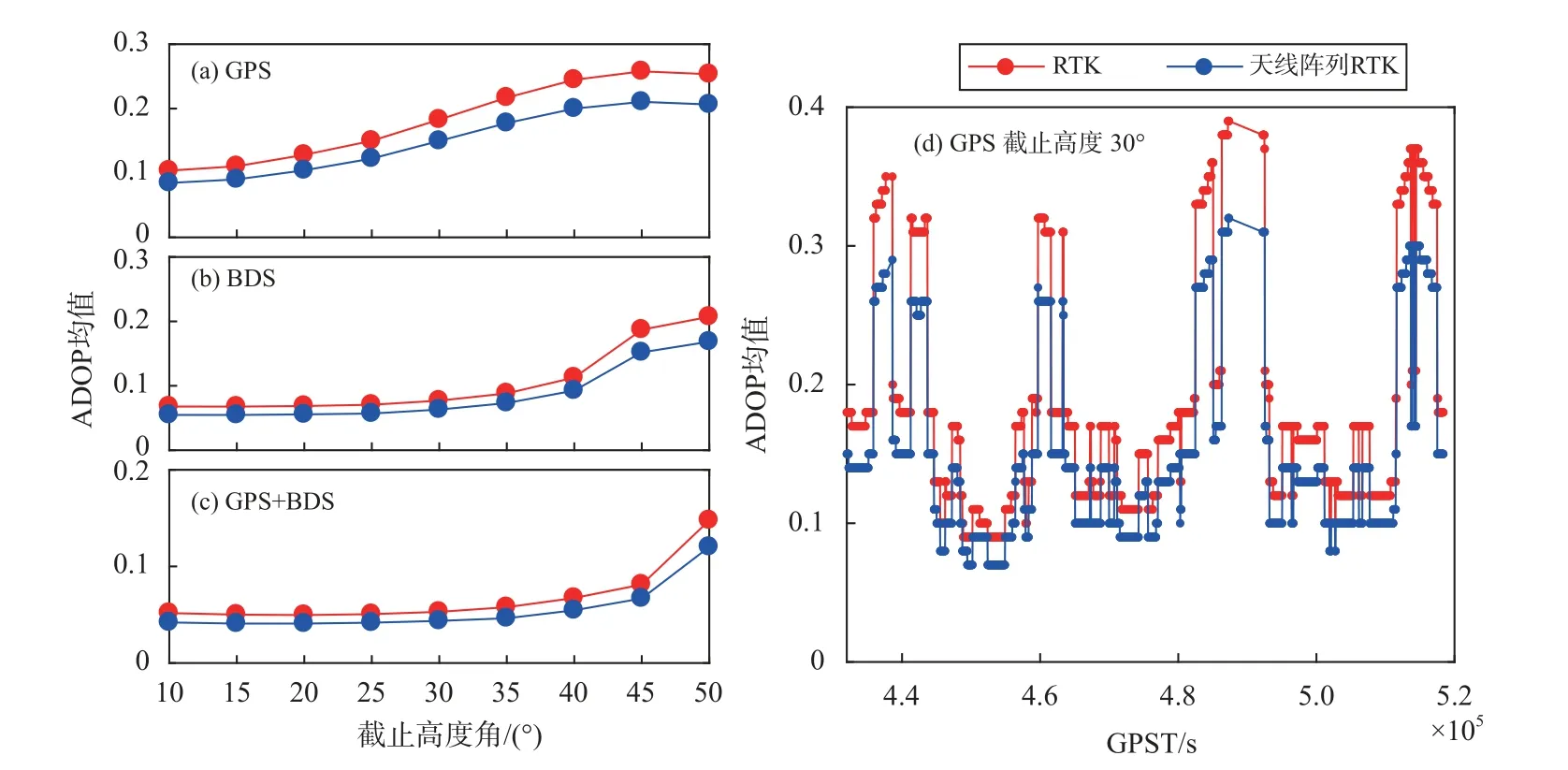
图5 不同截止高度角下RTK 和天线阵列RTK 计算的ADOP

2.3 定位精度分析

模糊度固定的最终目的是为了获得精密定位，并且由于GNSS 信号常受到周围环境遮挡，设置不同截止高度角能在一定程度上模拟城市峡谷或者林荫道路环境，接下来对不同截止高度角下天线阵列RTK的定位性能进行评估.

由表5 可以看出，相同截止高度角的情况下，与RTK 相比，天线阵列RTK 都能明显提高浮点解定位精度，其中当截止高度角为20°的GPS 单系统精度提升最少，为8.7%，在截止高度角为30°的BDS 单系统解算精度时提升最多，为27.1%.

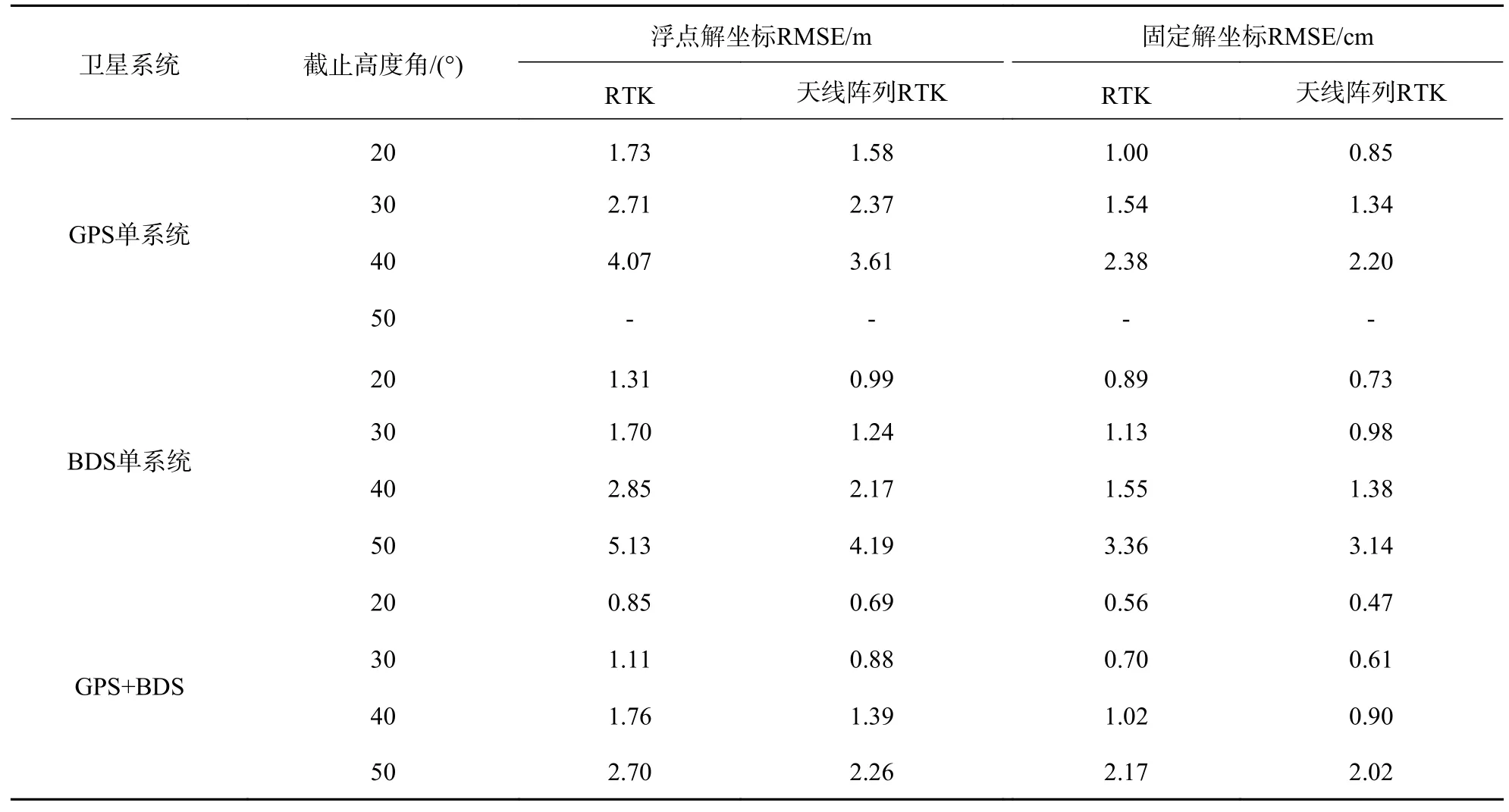
表5 不同截止高度角下天线阵列RTK 与RTK 三维坐标RMSE

图6 展示了截止高度角20°和40°时两种模型固定解在水平、垂直方向上的偏差，图中红色、蓝色散点分别代表RTK 与天线阵列RTK.可以发现天线阵列RTK 的定位精度更高，这是由于天线阵列RTK 增加了双差模型的冗余度，提高了模型强度，而GPS+BDS 的组合要优于GPS 单系统或BDS 单系统，这是由于双系统组合增加了卫星空间结构强度也提高了模型强度.开阔环境下常将截止高度角设置为20°或小于20°，此时GPS 单系统、BDS 单系统、GPS+BDS的解算率都为100%，且模糊度固定成功率接近100%，结果连续稳定，满足厘米级的定位需求.当高度角由20°增大到40°时，定位精度随之下降，GPS 单系统的定位结果不连续，而BDS 单系统与GPS+BDS仍能保持厘米级定位.

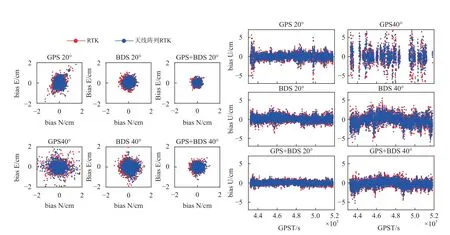
图6 截止高度角20°与40°时天线阵列RTK 与RTK 的固定解水平方向、高程方向偏差

表6 统计了更多截止高度角下东(E)、北(N)、天顶(U)三个方向上的定位误差，通过表2 可知，GPS单系统在截止高度角为50°时，解算率仅为17.6%，不能进行有效定位，因此表6 中未分析该情况的固定解.经分析，无论是单系统还是组合系统，天线阵列RTK 还是RTK，随着截止高度角的变化，均呈现出一定的规律和特点：首先在选取的截止高度角下，相同卫星系统下的天线阵列RTK 在E、N、U 方向上的RMSE 都小于RTK，说明天线阵列RTK 能够提高定位精度；特别是在截止高度为50°时，天线阵列RTK 的E、N、U 方向的固定解较于RTK 分别提高了7.7%、11.7%、6.7%.其次随着截止高度角变大，卫星数量下降，卫星的几何构型变差，在三个方向上固定解的RMSE均变大，但天线阵列RTK 在50°截止高度角时，其固定解水平精度优于1 cm，高程精度优于2 cm，仍能满足高精度定位需求.最后，结合表3中的PDOP 数据，即在相同高度角的条件下，BDS 单系统的定位精度要好于GPS 单系统，这可能是由于本次实验中同一高度角的BDS 可视卫星数要多于GPS 单系统，BDS 单系统的空间构型更好，同理，GPS+BDS 双系统组合的卫星空间结构要好于单独任意一个系统.

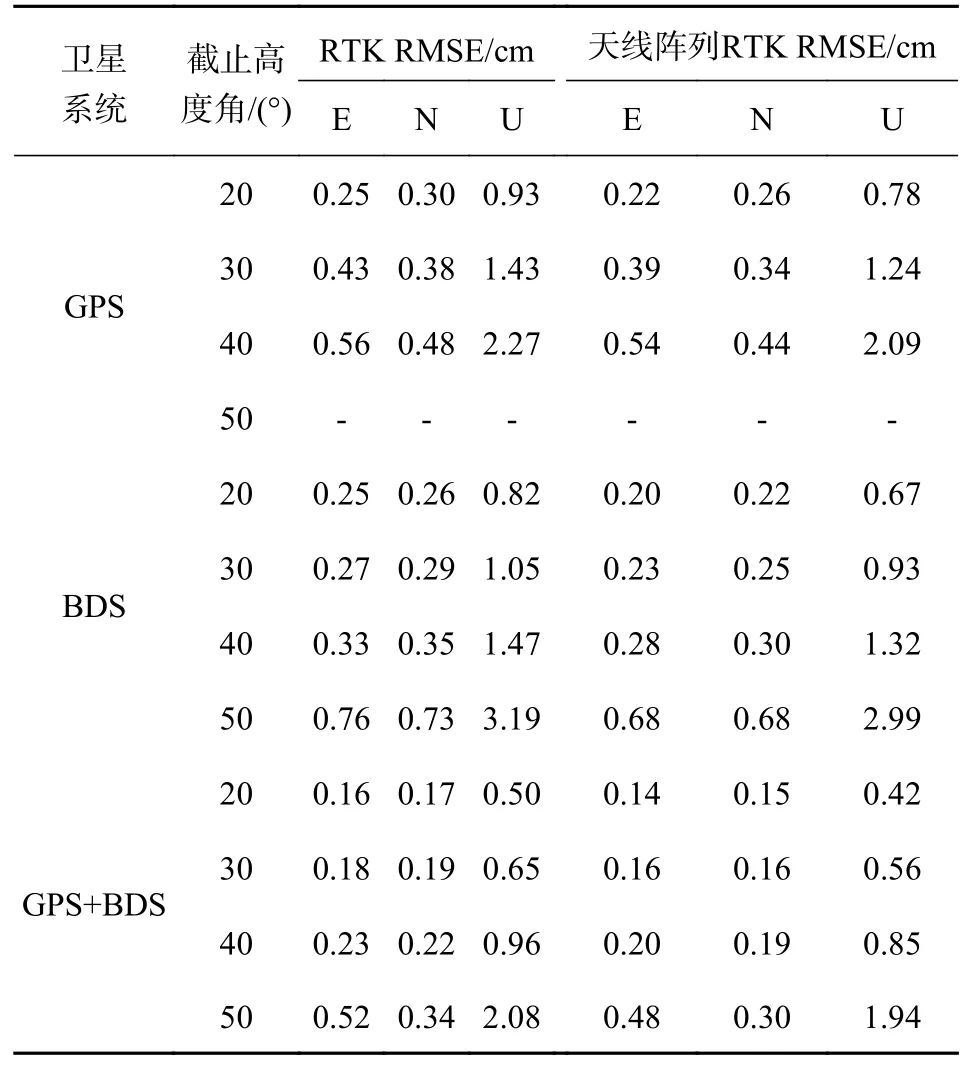
表6 不同截止高度角下天线阵列RTK 与RTK 固定解E、N、U 方向上的RMSE

3 结束语

本文针对天线阵列RTK 定位性能评估问题，对比了天线阵列RTK 和RTK 的数学模型，使用澳大利亚科廷大学GNSS 中心的观测数据，主要分析了20°～50°截止高度角下GPS 单系统、BDS 单系统以及GPS+BDS 的天线阵列RTK 模糊度固定与定位性能，并通过与RTK 定位结果对比得到以下结论：

1)天线阵列RTK 能够在每个历元现有的卫星条件下，充分利用观测信息.其关键技术是融合多个测站的伪距、载波相位观测值从而增加双差模型的冗余度，增加模型强度，进而提高模糊度固定成功率与定位精度.

2)天线阵列RTK 的表现优于RTK.当截止高度角较低时，天线阵列RTK 在模糊度固定方面具有微弱优势，而对浮点解定位精度的提升较为明显.例如单BDS 在截止高度角为20°、30°定位时，相较于RTK，天线阵列RTK 的浮点解定位精度分别提高了24.4%和27.1%，这对于只能使用浮点解的应用场景具有一定的研究价值.

3)在50°大截止高度角下，GPS 单系统、BDS 单系统的解算率分别为17.6%和78.5%，无法连续定位，而GPS+BDS 双系统组合的解算率大于99%，在此条件下天线阵列RTK 的模糊度固定率由RTK 的89.6%提高至93.6%，单历元固定解在E、N、U 方向上的精度分别提高了7.7%、11.7%和6.7%，并且其固定解的水平精度优于1 cm、高程精度优于2 cm，满足高精度定位的需求，因此天线阵列RTK 提高了RTK 在大截止高度角场景中(例如城市峡谷)的定位性能.