北斗全频段GNSS-R 水位反演研究

符平贵，匡翠林，楚彬

(1.中南大学地球科学与信息物理学院,长沙 410083；2.湖南省测绘科技研究所,长沙 410007)

0 引言

北斗卫星导航系统(BDS)作为中国自主建设、独立运行的卫星导航系统，与其他卫星系统相比，提供了更多的卫星信号，使得该系统具有全球卫星导航反射测量(GNSS-R)应用的巨大潜力.Jin 等[1]首次利用BDS 三频信号(B1I、B2I 和B3I)的信噪比(SNR)数据与三频相位组合反演海平面高度，与验潮站结果相比，相关系数为0.87～0.91，均方根误差(RMSE)小于0.6 m.Wu 等[2]研究了BDS 中地球静止规道(GEO)卫星的水位反演性能，实验结果表明GEO 卫星的时延多普勒和相位测高具有较高的反演精度，适用于监测海平面变化小的区域，且时间分辨率较高.陈发德等[3]基于MAYG 站的B1C、B2a 和B2 SNR 数据对水位进行了反演，实验结果表明BDS的三频数据反演精度略低于其他系统.Zheng 等[4]分析了多频多模GNSS-R 反演水位精度，结果表明北斗二号卫星导航系统(BDS-2) 地球同步轨道卫星(GEO)不适用于海岸水位反演，BDS-2 中轨道卫星(MEO)的监测精度优于BDS-2 倾斜地球同步轨道(IGSO)，北斗三号卫星导航系统(BDS-3)MEO 的监测精度与BDS-2 MEO 相当.Liu 等[5]对北斗系统SNR 反演水位高度的潜力进行了研究，但并未对B2b 和B2a+B2b等新信号进行水位反演.上述研究主要集中于如何提高反演精度和不同轨道高度卫星的测高性能，并未对北斗系统全频段的水位反演性能进行全面分析.

本文主要评估北斗系统全频段GNSS-R 水位反演的性能.首先描述GNSS-R 水位反演方法，然后对比频谱分析与非线性拟合算法的反演算法精度，在选择合适的反演算法基础上，引入Savitzky-Golay 滤波对北斗全频段反演结果进行滤波算法去噪，提升水位观测精度.

1 GNSS-R 水位反演方法

1.1 GNSS-R 水位反演原理

图1 为 GNSS-R 反演海平面高度原理图.图中h为天线相位中心(APC)到瞬时海平面的距离，θ 为直射信号与瞬时海平面的夹角.

图1 GNSS-R 反演海平面高度原理

为了有效地抑制测站周围反射物引起的多路径效应，直射信号和反射信号的振幅值需要满足如下的关系：

干涉合成信号振幅的总体趋势取决于卫星发射的直射信号的振幅Ad，而多路径引起的反射信号的振幅Am则表现为低高度角下的周期性波动.SNR 与干涉后合成信号振幅之间满足如下关系：

式中：Ac为GNSS 测站天线接收的合成信号振幅；cos ψ为直射信号与反射信号夹角的余弦值.

结合式(1)可知Ad与Am在数值上相差较大，通常利用低阶多项式去除SNR 的趋势项Ad.把图2(a)中的趋势项移除后，剩余项即可认为是受多路径影响所产生的SNR 振荡序列，如图2(b)所示，可利用其反演反射体的环境参数.SNR 振荡序列可表达为

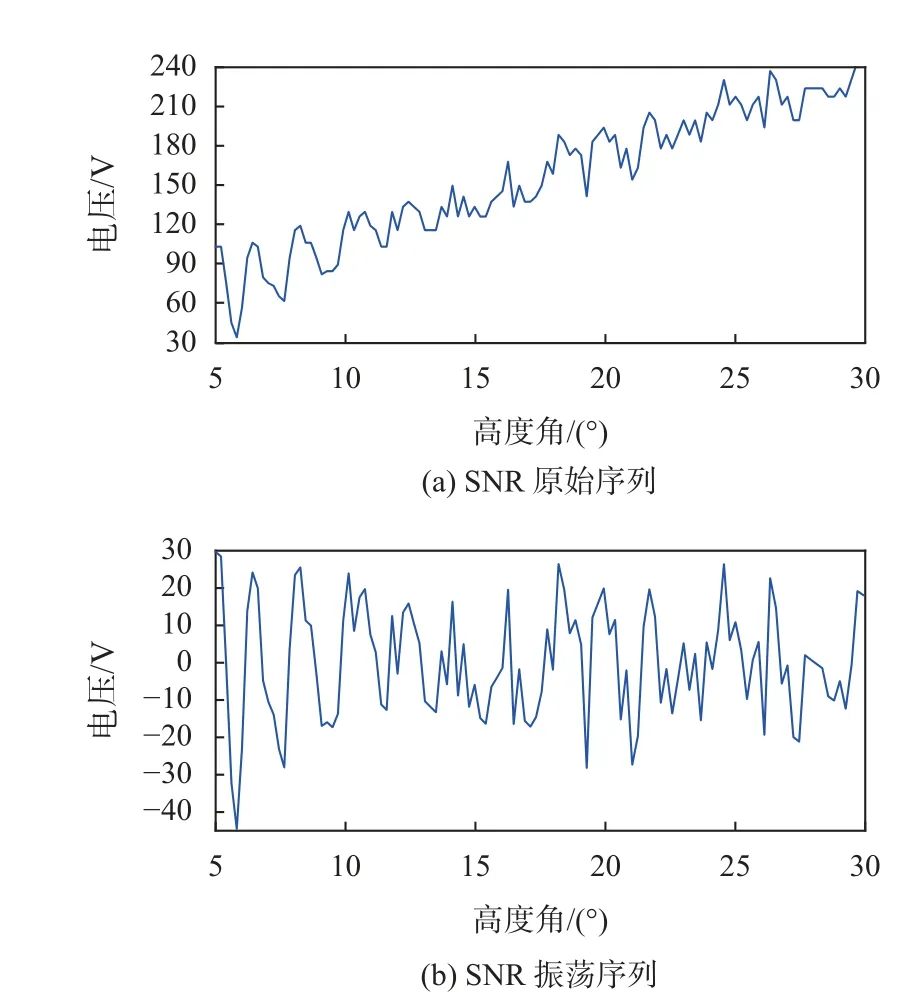
图2 SNR 观测序列

式中：A为 振幅值；h为反演的距离；λ 为波长；θ 为卫星高度角；φ为延迟相位.

由式(3)可知，水位反演就是依据 δ SNR 观测值求解h.Lomb-Scargle 谱分析和非线性拟合是两种常用求解h的方法，下面分别给予描述.

1.1.1 Lomb-Scargle 谱分析方法

设t=sin θ，f=2h/λ，则可将式(3)简化成标准的余弦函数形式：

由式(5)中可知，只需要求解出SNR 振荡序列的频率f即可反算出高度h.

SNR 振荡序列是以高度角正弦值为变量的不等间距信号，而且接收到的信号中存在噪声干扰.在应用傅里叶变换时，这些噪声和不均匀分布会对频谱分析产生影响，导致频谱图与SNR 信号的实际结果有很大偏差，甚至会出现虚假峰.Lomb-Scargle 频谱分析方法不仅可以有效地获得弱周期信号的频谱估计值、解决非均匀采样信号的频谱估计等问题，还可以克服数据缺失和序列长度不足等困难.下面简要阐述Lomb-Scargle 频谱分析方法.

对于时序序列X(tj)，j=1,2,3,··,N，其功率谱可定义为关于频率的函数：

式中：Px(f) 为 频率f的周期信号功率；X(tj) 为离散实验数据；tj为离散实验数据的时间；N为实验数据统计量；τ 为时间平移不变量.

1.1.2 非线性拟合SNR 信号方法

Strandberg 等[6]提出利用非线性最小二乘法求解海面高度，将式(3)添加一项衰减因子得到下式:

式中，γ 与反射体的性质有关.

为了保证有稳定的数值解，将式(7)转换为式(8)：

式中：C1与C2共同决定式(9)中的振幅A与式(10)的相位φ：

同理，基于SNR 振荡序列按照式(8)进行非线性拟合，即可求解反射高.

1.2 Savitzky-Golay 滤波去噪

受测站环境因素影响，GNSS-R 水位反演结果中不可避免会存在一些误差，导致反演精度下降.本文拟通过Savitzky-Golay 滤波算法[7]降低各种误差带来的影响.Savitzky-Golay 滤波是一种时间域范围内基于局部多项式的最小二乘拟合滤波方法，它能实现对数据特征的无衰减平滑.

下面对Savitzky-Golary 滤波算法进行描述.取某点附近的 2m+1 个 连续数据进行p阶多项式拟合，其中p≤2m+1，记该多项式为

式中：F(t) 为拟合后的多项式；bk为多项式系数；tp为多项式自变量的幂次方.

最小二乘法通过最小化RMSE 之和进行曲线拟合：

式中：S为RMSE；f(i) 为拟合前离散时间序列在第i点处的值.

为了使该误差平方项达到最小值，令误差表达式S对各系数求导数并使之为零，即：

因此，给定需要拟合的点数m和多项式阶数p，求解方程组(14)，就可以求出系数序列(bp0,bp1,bp2,··,bpp)，从而确定多项式F(t) .

使用Savitzky-Golay 滤波算法对反演结果序列进行去噪时，根据反演结果序列的特征选择合适的多项式阶数及窗口长度.本文选取窗口大小为21，曲线拟合阶数为3.

2 实验及结果分析

2.1 实验数据

实验采用国际GNSS 服务(IGS)SAS2 站的北斗系统SNR 数据进行水位反演，图3(a)为SAS2 站点环境，图3(b)为该站方位角80°～360°、高度角5°～30°的菲涅尔区，可看出GNSS 接收机距离水面较近，周边存在一些非水面反射.为客观评价北斗全频段的反演效果，同时选取距站点约8 m 的验潮站Sassnitz(http://www.ioc-sealevelmonitoring.org/station.php?code=sass)的实测水位作为验证数据.

图3 SAS2 站点环境及菲涅尔区

2.2 频谱分析与非线性拟合方法比较分析

本实验分别使用频谱分析与非线性拟合对SAS2 站2021 年年积日1～365 天的北斗全频段SNR数据求取反演结果并与该站GPS L5 的反演结果作对比，研究表明GPS L5 可取得较好的反演精度[8].通过将反演结果与验潮站实测水位进行对比分析以验证频谱分析与非线性拟合算法的准确性.实验选择了RMSE、相关系数、反演点数量(所有SNR 振荡信号拟合出的反演高度h的数量)作为GNSS-R 水位反演性能的指标.

上述实验结果相关统计指标如表1 所示.可以看出：频谱分析方法中B2a 频段反演效果相对于其他频段较差，B3 频段反演效果最优；非线性拟合方法中B1 频段反演效果相对于其他频段较差，B3 反演效果最优；非线性拟合方法的反演结果都相差不大，其中RMSE 最大与最小的差值为7 cm，而频谱分析方法RMSE 最大与最小的差值达到了9.6 cm.北斗全频段中通过非线性拟合的反演结果中，除B1C、B1、B2a 的RMSE 相对GPS L5 的RMSE 平均提高了0.87 cm，其余频段的RMSE 都优于GPS L5 频段.而频谱分析方法的B2a 和B2b 的RMSE 相对GPS L5 的RMSE 平均提高了2 cm.虽然非线性拟合方法得到的B1C、B1、B3 的反演精度略低于频谱分析，但其反演时间分辨率均高于频谱分析，且其余频段反演精度均高于频谱分析，尤其B2a 频段的RMSE 相对于频谱分析提高了17.05%.

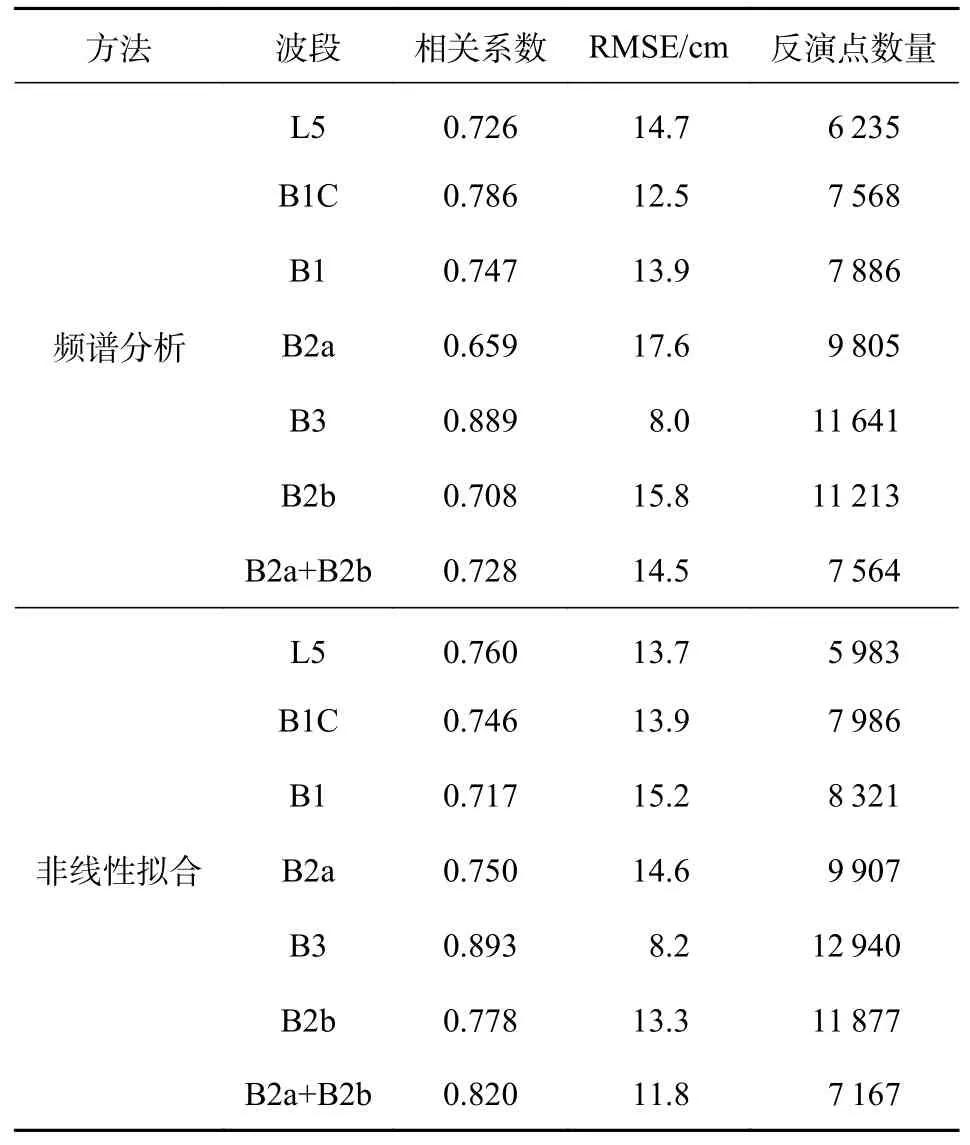
表1 北斗全频段水位反演结果统计信息

2.3 水位反演结果Savitzky-Golay 去噪

受测站环境因素的影响，水位反演值中不可避免地会带来误差，本文使用Savitzky-Golay 去噪算法降低误差影响.对2.2 节中每个频段的非线性拟合反演结果进行去噪处理，去噪前后的反演结果如图4 所示.图中仅展示了SAS2 第1 天到第30 天滤波前后水位数据与验潮站实测数据的对比，可以看出去噪后的反演结果明显与验潮站实测水位数据更加符合.图5 展示了滤波前后水位数据与实测数据的残差图，可以看出,滤波前的误差图中反演误差变化范围较大；而使用Savitzky-Golay 去噪后，反演误差变化范围小于滤波前的误差变化范围.

图4 水位反演结果与验潮站数据对比

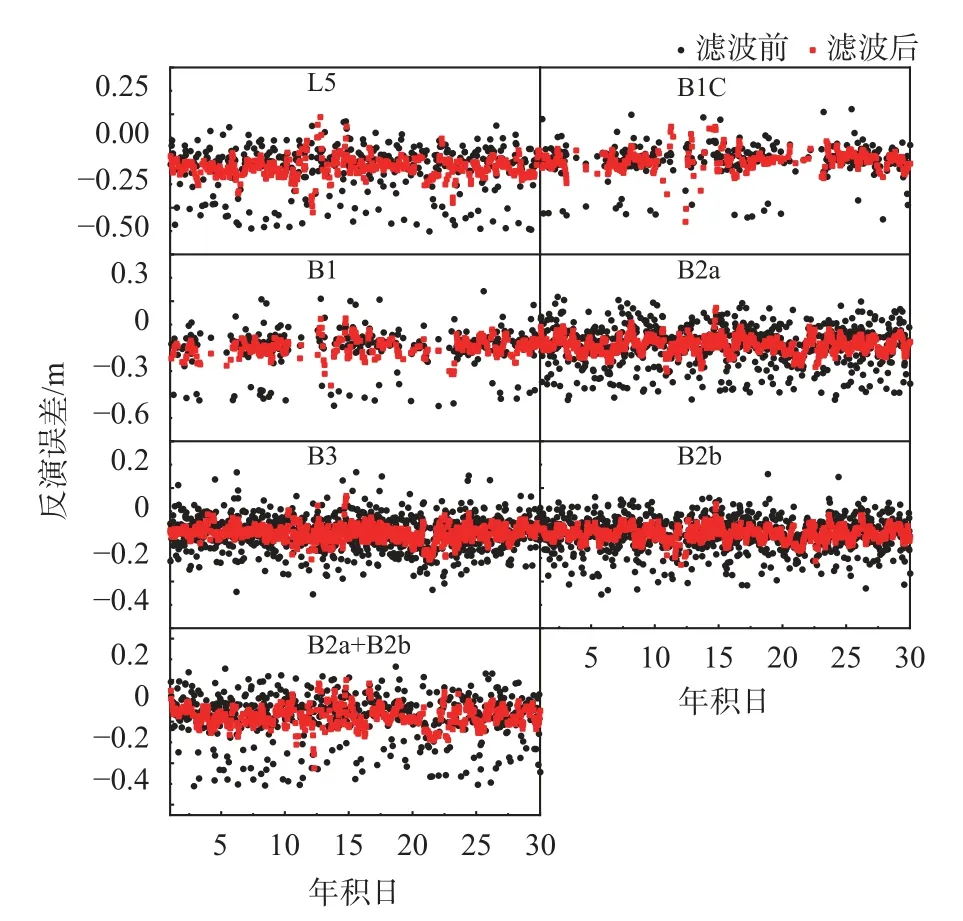
图5 水位反演结果相对验潮站数据的偏差

去噪前后的结果与验潮站实测水位的统计结果如表2 所示.可以看出，经过Savitzky-Golay 去噪处理后的水位反演精度均有很大提升，去噪后北斗全频段的RMSE 相对去噪前的RMSE 平均减少了7.4 cm，其中提升效果最显著的是B2a 频段，其RMSE 减少了9 cm，相关系数平均提升了16.40%.

表2 GNSS-R 滤波前后精度统计

为提高水位监测的时间分辨率和精度，考虑到北斗不同频率之间的互补性，将北斗系统全频段的反演水位组合在一起.图6(a)是北斗全频段反演水位值组合，可以看出反演点数量明显增加，且时间分辨率相对于单一频率的时间分辨率更高，其RMSE 为5.4 cm，优于B1C、B1 以及B2a 频段.图6(b)为反演值与验潮站相关性分析，可以发现相关系数优于B1C、B1以及B2a 等频段，与验潮站实测数据有良好的一致性.总的来说，直接将北斗系统不同频率的反演结果组合，可达到提高精度和时间分辨率的目的.

图6 北斗全频段水位反演组合结果与验潮站比较

3 结束语

本文系统评估了我国北斗全频段SNR 数据的GNSS-R 水位反演性能.首先比较了两种常用的反演水位算法的精度，实验表明非线性拟合方法综合效果优于频谱分析方法，虽个别频段反演精度略低于频谱分析方法，但非线性拟合方法的反演点数量多于频谱分析方法.然后，针对反演结果中存在随机误差较大，本文通过Savitzky-Golay 算法对反演的水位结果进行了滤波去噪，数值表明滤波后反演水位的RMSE 极大降低，达到厘米级，且提升了与潮位数据的相关性.整体上，北斗全频段的反演性能与GPS L5 相当.