GNSS 反射信号陆面遥感应用综述

2023-07-31杨东凯李杰

全球定位系统 2023年3期

杨东凯，李杰

(北京航空航天大学,北京 100191)

0 引言

全球卫星导航系统(GNSS)发展至今已有半个多世纪，已被广泛应用于人民日常生活和生产实践中.GNSS 提供的强大定位、测速以及授时能力大大改善了生产效率，也提升了人们日常出行的效率和安全度，日益增长的位置服务需求则进一步推动了GNSS 的完善和发展.对于北斗卫星导航系统(BDS)，除定位、测速和授时外，其短报文功能还可以进行数据传输，在灾害救援紧急情况下是已有通信系统的备份和补充[1].

GNSS 的核心是将无线电发射机置于卫星平台上，GNSS 卫星轨道高度约为20 000～36 000 km.对于地面或近地球表面的用户，接收到的无线电信号中除直射路径的信号外，也可能包含来自用户附近的地面或高楼大厦及其他目标的反射路径信号.早在20 世纪80 年代有学者于海边开展定位实验，发现了海表面波浪、海风与接收机输出信号之间的相关性，提出了利用反射信号进行海面遥感的想法，GNSS 反射信号遥感由此应运而生[2].

1993 年欧空局Martin Manuel 教授发表的一篇文章系统论述了GNSS 反射信号的应用[3]，之后该领域的研究便如雨后春笋般涌现出来，世界各地多家单位开展了地基、空基和星基试验，并专门开发特定的接收机进行应用测试，领域逐步拓展至海洋、气象、农业和环境探测等[4-7].

国内的研究最早始于科技部资助的863 计划(2002AA639190)[8]，2003 年在北京航空航天大学电子信息工程学院导航团队(现为定位导航和遥感应用实验室，简称PNaRL 实验室)的集中攻关下，成功研制了机载特定GNSS 反射信号接收机，并于2004 年在天津海域成功试飞.之后软硬件历经改版，飞行高度也由3 000 m升至5 000 m，并完成了大量地基、岸基应用试验，相关成果于2012 年编辑成书，由国家科学技术专著出版基金资助，并由电子工业出版社出版[9].

文献[10-12]分别较为全面地介绍了国内GNSS反射信号的发展概况.近年来国内相继有很多学者整理研究成果成书出版，其中较有代表性的有文献[13-17].

本文着重从GNSS 反射信号概念、特点和对地观测应用的角度方面进行阐述.为了解GNSS 反射信号模型、接收机处理方法、挖掘应用提供初始参考，并根据国内外研究热点方向和自身课题组的研究方向提出应用发展的一些思考.

1 GNSS 反射信号概念

1.1 GNSS 反射信号(GNSS-R)模型

GNSS 在距离地表2 000～20 000 km 的中轨地球轨道(MEO)，或在35 786 km 的地球同步轨道(GEO)发射右旋圆极化的电磁波，其载波频率为L 波段(1 100～1 600 MHz)，带宽有2 MHz、4 MHz、20 MHz和50 MHz 等，调制方式也有多种.搭载导航信号的电磁波经过地球表面反射后，电磁波的极化、幅值、频率和相位等4 个特征参量会发生改变，且和直射信号有明显的差异.分析直射信号和反射信号的差异依赖于反射信号的数学描述和接收机反射区及导航卫星三者之间的几何关系.

1.1.1 发射信号数学表达式

假设卫星导航发射至地球表面的载波信号为

式中：A为幅度；d(t) 为导航电文；c(t) 为扩频码；ω 为载波中心频率；φ0为初始相位.

同样的，GNSS 接收机接收到的自地球表面的反射信号可写为

式中：Ar为接收机天线处反射信号的幅度，和A相比增加了地球表面的吸收和自地面至接收机的自由空间衰减，可表示为

式中：fa为幅度函数；h为接收机天线至地球反射表面的高度；β 为反射系数.

ωr为反射信号至接收机天线处的频率，可建立如下的关系：

式中：fω为频率函数；vr为接收机的速度.

φr0为反射信号至接收机天线处的初相位，与φ0关系可表示为

式中，fφ为相位函数.

由式(3)～(5)可知，接收机中用于接收反射信号的天线与反射面的垂直距离(高度)h对幅度、频率和相位三者均有影响.

因导航电文数据率较低，式(2)中dr(t) 的处理相对较为简单，此处不作详细讨论.对于cr(t) 的处理，其关系式和式(4)类似，为

式中，fc为扩频码函数.

1.1.2 反射信号传播几何关系

GNSS 信号以视距(LoS)可见路线自卫星传播至接收机.反射信号的反射面和接收机也要保持在可视空间内，确保接收到的反射信号中仅有特定反射面的物理状态信息.简化的GNSS 反射信号几何关系如图1 所示.

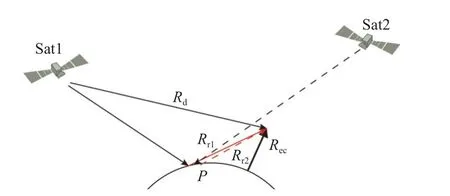
图1 简化的GNSS 反射信号几何关系

图中，Sat1 和Sat2 表示卫星导航，Rec 表示接收机，P为地球表面任一反射点，Rd为导航卫星至接收机的直线距离，Rr1为导航卫星至反射点的直线距离，Rr2为反射点至接收机的直线距离.显然，利用Rd、Rr1和Rr2三者之间的几何关系即可由卫星导航位置、接收机位置确定反射点的位置.

由于地球为椭球形，其表面并非平面，地球曲率的影响对GNSS 反射信号几何关系的描述和求解要计入在内，尤其是对于星载情况，GNSS 接收机位于几百千米高度的低轨卫星上需重点考虑.

另外，还需特别强调，若导航卫星相对反射点P位于接收机Rec 同侧(Sat2)，则收到的反射信号为后向信号；相对反射点P位于接收机异侧的导航卫星反射信号为前向信号.

1.2 GNSS-R 特点

1.2.1 极化反转特性

卫星导航发射的信号极化特性为右旋圆极化，可分解为垂直和水平两个线极化分量.经地球表面反射后，部分电磁波的极化特性变为左旋圆极化，即GNSS 信号的极化特性变为椭圆极化，具体各分量的比例构成则和信号的入射角(或导航卫星的高度角)有关.图2 为卫星高度角为0°～90°时反射信号不同极化分量的反射系数模值示意图，反射系数越高表示其所占比例越大，其中反射面为平坦的土壤表面.

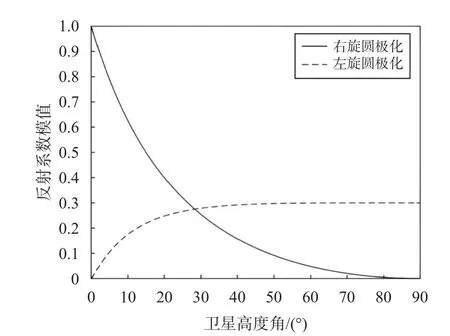
图2 不同极化分量反射系数模值随卫星高度角变化

在具体的应用场景中，反射信号中左旋圆极化和右旋圆极化分量将呈现不同的比例，比例值和反射面的材质、含水量以及粗糙程度均有一定的关系.

1.2.2 幅度衰减特性

假定导航卫星发射至地球表面的信号功率为Ps，经过反射后接收机收到的功率为Pr(包含接收机天线的增益)，则表面反射时的信号衰减以及反射后的路径传输衰减可等效为一个“黑盒”系统来分析，如图3所示.

图3 GNSS-R 信号的功率衰减模型

由Ps到Pr的功率衰减系统传输函数可表示为

式中：功率Ps和卫星导航与反射面的距离有关；Pr和反射面的介电特性、与接收机的距离以及天线增益有关.一般情况下，随着接收机与反射面的距离不同，需要配置的天线增益也不同，距离越远需要的天线增益越大.

GNSS 信号的幅度随卫星高度角改变，一般用功率来衡量，即能量的时间平均效应用来表征信号幅度的变化特点.进一步由式(7)可得：

式中：α 反映自反射面至接收机直线距离的信号衰减程度；β 为反射面的反射系数，反映其对L 波段电磁波的衰减程度；G为接收反射信号的天线增益.在图3 所示模型中，β 参数包含了地球表面反射面的物理特性，是求解的核心.此处需要指出的是，GNSS-R应用是非合作的，故本文不对GNSS-R 天线的增益作分析.

1.2.3 时间延迟特性

GNSS-R 的另一个关键特性是时间延迟特性，这是除能量衰减的另一个最为直观、简单的观测量.作为基于测时测距的导航定位系统，GNSS-R 和直射信号之间的传播时间延迟量比较容易计算，不管是利用前向散射还是后向散射，测量时间延迟的几何关系均由图4 实现.为方便分析和阐述，图4 假设地球表面为平面，绘制前向散射的几何关系示意图，并标注各个距离量和观测角度.

图4 地球表面为平面情况下的前向散射几何关系示意图

图4 中 θ 为地球表面镜面反射点处的卫星导航高度角.由于卫星导航离地球的距离远远大于镜面反射点和接收机间的距离，接收机天线和地面镜面反射点接收到的导航信号电磁波束可视为相互平行.假定接收机反射天线与实际发射面的垂直距离(高度)为h，则有

注意，图4 中GNSS-R 接收机的天线视为一个点，即直射天线和反射天线之间的间隔忽略.在实际工程应用中，直射和反射天线之间的间隔固定，可通过几何方法消除影响.式(9)中，(r1+r2) 为反射信号的传播距离，需要特定的开环接收处理方法求解[18].直射信号的传播距离d用传统的GNSS 接收机处理方法即可获得.

当GNSS-R 接收机安装在低轨卫星上时，镜面反射点的计算要复杂一些[19]，地球模型也要考虑曲率的影响，但是其电磁波的传播时延获取方法和式(9)仍然类似，只是各个观测量需要重新界定.

1.2.4 干涉特性

当来自相同发射源的两个波束以不同的传播距离到达同一点时会发生干涉现象，而干涉条纹的特征和两个波束的距离差有关.对于地基情况，当仅使用右旋圆极化的导航天线时，GNSS 直射信号到达接收机天线与经地面反射后再到达接收天线后在频率上几乎没有差别，则会产生干涉.GNSS 直射和反射信号或相互加强，或相互减弱，形成随卫星高度角变化的振荡.如图5 所示为GPS 32 号卫星高度角变化时地面固定接收天线所收到的信号干涉效果示意图.

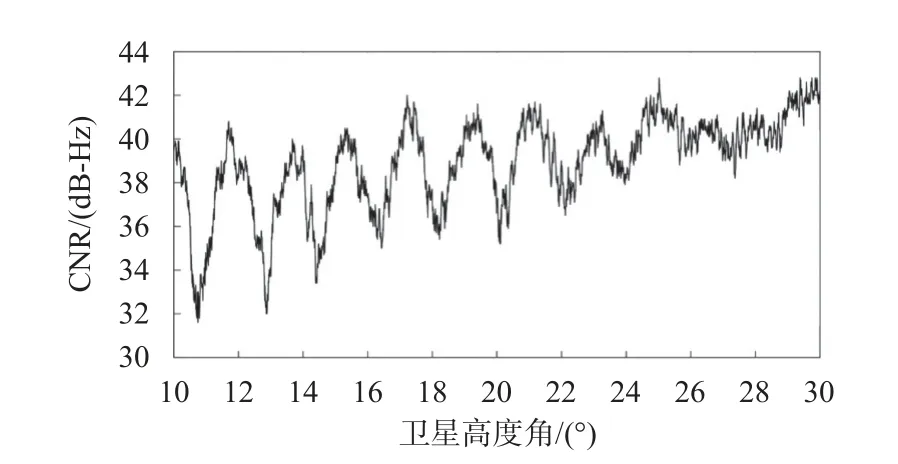
图5 卫星导航信号干涉效果示意图

图5 中，横轴为卫星导航高度角，纵轴为载噪比(CNR)数据.很明显，CNR 数据呈现类似正弦函数的波形变化.从此波形中提取的频率、幅值或者相位信息则可用于求解地面物理特性，如土壤湿度；也可以用于求解接收天线离地面的垂直高度，从而获得反射面的高度，也包括植被的高度、积雪深度等参量.

在通用的GNSS 接收机中，若满足一定的条件，则右旋圆极化天线收到的信号中必定包含附近地面反射的信号.无论反射信号的极化特性如何，当其能量足以和直射信号发生干涉时，干涉特性就可以在GNSS-R 遥感中应用.

2 GNSS-R 陆面遥感应用

2.1 土壤湿度反演

双天线GNSS-R 进行土壤湿度的反演首先分别采集直射和经过土壤反射的GNSS 信号，并建立直射和反射信号的相干特征量和土壤介电常数的关系，进一步反演土壤湿度.

2000 年，Zavorotny 等[20]利用土壤介电常数模型和双基散射模型对粗糙地表散射的GPS 信号进行了仿真分析.仿真得到的GPS 信号相关功率对土壤湿度敏感，可以用来提取土壤介电常数，进而反演土壤湿度.此外，该技术还可以在机载和星载平台上进行土壤湿度遥感.2008 年，Li 等[21]提出了一种基于GPS 双基地雷达方法测量海滩土壤水分的方法.该方法的核心在于用微弱信号CNR 的最大后验概率估计来提高CNR 估计的准确度，实验结果验证了该方法的可行性.而后，严颂华等[22]在介绍L 波段土壤介电常数模型的基础上，结合基于电磁散射几何光学近似模型的归一化反射功率、入射角以及介电常数的关系，开展了短期地基验证实验，反演得到的土壤湿度平均值与实测值相对误差为6%.2018 年，杨磊[23]建立了土壤粗糙度修正模型，并构建了修正地表粗糙度影响的双天线模式GNSS-R 土壤湿度反演的解析模型和基于人工神经网络的模型.仿真结果表明，当土壤粗糙度超过0.01 m 时，对粗糙度的修正是非常必要的.2023 年，Dong 等[24]通过tau-omega 模型修正了土壤粗糙度和植被对土壤湿度测量的影响.经过校正后，在植被覆盖下的土壤湿度测量精度得到了明显的提升，测量的分辨率可以达到0.046 cm3/cm3.

利用GNSS 干涉反射测量(GNSS-IR)也可以进行土壤湿度的反演.2008 年，Larson 等[25]提出利用GNSS 干涉信号进行土壤湿度测量的方法.他们发现在土壤表面相对平坦、天线架设高度较低的情况下，直反射信号间的频率近似相等、相位差也相对恒定，在GNSS 天线处会形成稳定的干涉信号.而后，各国学者展开利用GNSS 干涉信号进行土壤湿度反演的研究.Larson 团队还自行组建了一些类似板块边界观测(PBO)观测站的站点，并配备了相应的土壤湿度探测仪.2018 年，Han 等[26]提出了一种利用半经验模型拟合干涉信号的方法，从信噪比(SNR)数据中重建了直射信号和反射信号，进一步提升了土壤湿度的反演精度.2020 年，Hong 等[27]提出了一种利用GNSS伪干涉反射法(GNSS-PIR)测量土壤湿度的方法.他们将右旋圆极化天线接收到的信号与左旋圆极化天线接收到的信号相结合，形成振荡CNR 波形，模拟了GNSS-R 的干涉特性，最终证明了GNSS-PIR 测量精度高于传统GNSS-IR.

除了传统的方法，利用GNSS 信号透射进入土壤时的特征参量变化情况也可以测量土壤湿度.2016 年，Koch 等[28]利用GPS 信号穿透土壤时的功率衰减进行了土壤湿度的反演可行性，证明了GPS 信号功率衰减的程度与土壤湿度有很强的相关性.2020 年，汉牟田等[29]使用两个相同规格的GNSS 天线，其中一个埋入土壤内部，另外一个放在开阔空间，并且不断改变土壤的厚度和湿度进行实验.结果表明，土壤的湿度值与厚度值越大，GNSS 透射信号功率衰减越严重.2022 年，李杰等[30]建立了GNSS-R 信号穿透土壤深度与土壤湿度的关系，并利用传统GNSS 反射信号测高原理计算出信号穿透土壤的深度，从而实现了土壤湿度的反演.同时，他们利用归一化植被指数(NDV1)对测量结果进行了修正，进一步提高了反演的精度.

2.2 植被含水量反演

植被在水土保持中起着重要作用，与气候、碳平衡和土壤肥力等自然因素密切相关[31].归一化植被指数(NDVI)是一个广泛使用的区域植物生长和空间分布密度指标[32].然而，通过大规模NDVI 很难获得短期的、高分辨率的植被密度和生长情况.由于L 波段信号的波长较长，容易穿透植被，而这种穿透与植被覆盖密度和生长状态有关，因此反射的L 波段信号由植被冠层和土壤表面反射信号分量组成.随着植被覆盖密度的增加，植被反射的信号分量增加，土壤表面反射的信号分量减少.因此，植被密度会影响L 波段信号的反射率，所以L 波段反射信号可以用来测量植被密度和生长.

2014 年，Larson 等[4]使用GNSS 反射信号的归一化微波反射指数(NMRI)来估计植被含水量，并使用PBO 网络的数据进行了验证.首先计算出L1 和L2 波段的多路径误差，结果表明多路径误差几乎不受电离层的影响，且发现NMRI和NDVI 具有很好的正相关特性.2016 年，Chen 等[33]采用定制的偶极子天线采集GNSS-IR 信号，并在美国科罗拉多州博尔德市进行了植被含水量的反演实验，在利用双天线GNSS-R 进行植被遥感方面取得了大量的成果.2019 年，Eroglu 等[34]基于相干双基地植被散射模型(SCoBi-Veg)模拟了玉米在整个生长季节下不同土壤湿度、植被含水量和表面粗糙度下的GNSS-R 特征.同年，Yang 等[35]证明了利用BDS SNR 数据测量土壤湿度、植被含水量和积雪深度等方面的潜力.研究了BDS 干涉SNR 的相位、幅值和有效反射面的高度与同比的地表参数的相关性.结果表明，BDS 的B1 和B2 两个频率都可以较好地反应植被含水量的波动，并且对于植被高度，B2 信号比B1 信号能提供更好的测量效果.

在陆面遥感应用中，土壤和植被测量的相互影响往往不可忽略.部分学者研究了土壤表面和植被冠层反射信号的特征差异，建立了考虑土壤湿度的植被含水量反演模型.2017 年，Zhang 等[36]提出了基于SNR优势频率的植被高度反演算法.实验结果表明，当归一化SNR 低于0.78 时，可以将土壤表面反射的GNSS信号视为优势信号；相反的，则植被冠层成为优势反射面.2022 年，Li 等[37]将土壤湿度作为先验条件，建立了GNSS 信号反射率的修正模型，并利用PBO 站点的数据进行了验证，结果表明，对于平坦的地形，模型可以更好反演植被的生长状态；但对于崎岖的山地和大雪覆盖的情况，利用土壤湿度修正的效果较低.

此外利用GNSS 信号的极化特性也可以进行植被含水量和土壤湿度的同时测量.2021 年，Wu 等[38]采用一阶辐射传递方程模型，根据波合成技术建立模型，得到各种极化组合.他们采用该模型模拟了所有潜在的机会源信号的反射波段，即圆极化和线性极化的P 波段、L 波段、C 波段和X 波段的双基地散射模型，并建立了土壤湿度、土壤粗糙度、植被含水量等地表参数与双基地雷达截面之间的关系.

同样的，利用GNSS 信号穿透植被后特征参量的变化也可以进行植被含水量的反演.早在2012 年，Alvarez 等[39]在一片核桃树林里进行了实验，在树下和露天的位置分别放置了两个相同的GNSS 天线.结果表明，功率衰减可以有效地提取植被叶片含水量信息，也是GNSS 透射信号测量植被含水量的萌芽.而后，Guerriero 等[40]提出了一种利用晴朗天空和植被冠层下两个相同规格右旋圆极化天线采集的GNSS直接信号提取森林信息的方法.他们对三个生物量不同的杨树林进行了一项实验，以验证利用GNSS 信号衰减反演植被状态的可行性.结果表明，在冠层下采集的信号相对于开阔天空采集的信号会受到植被衰减和去极化的影响，证明了直接视距传播和体积散射对信号的幅值及其时间波动都有影响.虽然实验数据集的大小和环境条件有限，但两种反演算法也得到了令人鼓舞的测量结果.Camps 等[41]从衰减和去极化两个方面分析了植被对GPS L1 C/A 信号的影响.该团队在森林中安装了双极化的天线，GNSS 接收机采用COTS GPS 接收器，用于收集CNR 数据，安装时间超过一年.将采集的CNR 数据与NDVI 进行了对比，结果表明两者的相关性很高.实验结果还表明，在卫星仰角接近50°的时候去极化的效应最显著.还研究了tao-omega 模型补偿植被的效果，发现在卫星仰角较低的时候该模型与NDVI 无关.2022 年，Li 等[42]利用单天线透射信号功率衰减测量了玉米叶片的含水量.他们根据玉米生长周期，选择叶片开始覆盖GNSS 天线的时间作为基准.实验结果表明，单天线也可以进行玉米叶片含水量的测量，其相关系数达到了0.92.

2.3 雪深测量

积雪是冰冻圈中覆盖范围最广、最活跃的要素，按照积雪存在的时间，可以分为永久积雪和季节积雪[43].2008 年，Jacobson[44]首先提出了利用GPS反射信号进行积雪深度的测量，验证了GNSS 在积雪测量中的潜力.同年，Larson 等[45]利用这项研究使用了单个的用于抑制反射的右旋圆极化GNSS 天线，首次证明了GNSS 干涉信号可以进行积雪深度的测量.2013 年，Nievinski 等[46-47]在积雪场地进行了长期实验，结果表明评估得出的相关性为0.98，对于观测到的雪深达2.5 m 时，均方根误差(RMSE)为6～8 cm.2014 年，Boniface 等[48]利用PBO 的数据进行了GNSS-IR 反演雪深的验证.他们对100 多个PBO 站点的数据进行验证，结果表明，超过80%的站点反演的雪深均与积雪监测站的数据有着较好的相关性.2018 年，郑中天[49]针对GPS-IR 反演雪深中存在的系统偏差和跳变问题，提出了一种基于GA-BP 神经网络优化的方法.通过调整GA-BP 的参数，反演和同位测量的雪深相关性达到了0.95，证明了利用GA-BP模型对GPS-IR 反演雪深进行修正的可行性.2021年，彭继轮[50]设计了一种基于GNSS-IR 测量积雪深度的软件，该软件提供数据质量检查、反射点轨迹和菲涅耳区域的映射、干扰信号的可视化和光谱分析，以及基于SNR 和时空载波相位观测的雪深估计.同年，李政[51]将快速傅里叶变换(FFT)频谱分析与非线性最小二乘拟合引入Lomb-Scargle Periodogram(LSP)频谱分析中，建立了更加精确的雪深反演模型；并定量分析了地面倾斜度对反演精度的影响，将反演精度提高了11.6%.2022 年，陈亮宇等[52]借鉴零基线模式，在中国北极黄河站进行了GNSS 干涉信号雪深反演实验，探讨并研究了GNSS 接收机的测量精度对积雪深度反演的影响.他们使用两个不同规格的接收机采集三个不同频点的GNSS 信号进行雪深反演，反演的结果存在一定的差异，尤其是当积雪深度变化较大时，差异更加明显.

使用GNSS-R 技术也可以进行积雪深度的反演.2012 年，Gutmann 等[53]在美国科罗拉多州进行了GNSS-R 的雪深测量实验.他们采用激光雪深深度探测系统进行同位数据的测量，并且采用人工测量的方式同步进行测量.结果表明，利用GNSS-R 用于积雪深度测量在测量精度和数据连续性上有着很大的优势.2015 年，邵礼明等[54]分析了GNSS-R 测量干雪的可行性，他们分析了欧空局在南极洲收集的干雪实验数据，结果表明干雪深度分别约为10 m、85 m、135 m、225 m 时的反射信号可以在频谱上形成明显的峰值.2016 年，张双成等[55]基于GPS-MR 测雪原理，分别分析了利用单颗和多颗GPS 卫星的雪深测量精度.结果表明，基于SNR 观测值的GPS-MR 技术在暴雪监测中有着较高的精度.2019 年，黄良珂等[56]分析了利用GPS L5 信号反演雪深的可行性，发现利用GPS L5 信号测量精度要明显高于GPS L1 信号.2022 年，张志等[57]构建了一种融合VMD 算法的多星GNSS-MR 雪深反演模型，与传统的二阶多项式拟合模型相比较，反演值与实测值的RMSE 降低了近50%，相关系数高达0.98.2023 年，Zhang 等[58]分析了由于信号穿透导致的雪深测量误差，并提供了系统负误差的物理解释，确定了雪深差和SNR 指标的基线和短期变化，并研究了它们在不同雪期的关系.结果表明：稳定期和融化期的系统负误差和SNR 指标分别以降雪的层状结构和液态水含量为主.

2.4 陆表水体识别

GNSS-R 遥感在水体识别上的研究起步较晚，并且地基GNSS-R 技术测量的区域受限.基于GNSS-R的陆表水体识别往往使用机载和星载的方式，2018 年，Chew 等[59]基于CYGNSS 数据绘制了较高分辨率的地表洪水分布图，对比SMAP 得到的结果，利用CYGNSS 可以有效地提高洪水分布测量的时空分辨率和更加清晰的饱和度.宁美玲[60]分析了在不同环境下GNSS 信号受影响的情况，对地面异常情况进行了识别.2020 年，Lowe 等[61]在德克萨斯州卡多湖上空进行了一次飞行实验，来测量植被覆盖下的土壤湿度.实验过程中发现，湖泊和河流反射的GNSS信号反射率更高、相干分量更多.证明了采用机载GNSS-R 进行陆表水体识别的可能性.由于机载实验要求较高，各国学者将目光投向了星载实验.2021年，Marzi 等[62]通过CYGNSS 卫星的DDM 创建了动态的陆表水体掩膜，将Pekel 水体掩膜作为同位数据，结果表明，水体的识别率达到了80%.2022 年，陈璞等[63]提取地表反射率参数作为特征值，建立了信号反射模型和洪水模型的关系.结果表明，通过GNSS-R 对洪水有较强的敏感性，可用于进行洪水探测.同年，Wang 等[64]提出了一种利用CY-GNSS-R提供的延迟多普勒图(DDM)测量来绘制内陆水体的新方法，结果表明，与参考光学水掩模相比，亚马逊盆地整体检测精度为94.48%，水检测精度为92.23%.Morris 等[65]开发了以概率方式表示来自CYGNSS观测的信息的方法，并使用一个逻辑回归模型来估计CYGNSS 观测的地表水概率，获得了较好的识别效果.Yan 等[66]基于GA-LinkNet 进行了内陆水域的绘制，并使用CYGNSS 的数据进行验证，结果表明对水体覆盖率较高的区域绘制更加精准.

2.5 河流遥感

利用GNSS-R 进行河流边界探测是近几年的一个新的研究方向，学者们进行了相关的仿真和实验，验证了该项技术的可行性.

白伟华等[67]首次开展了机载河流GNSS-R 遥感.他们利用GPS 双频差分定位进行了河流表面的测高，并且通过从GNSS-R 的残差相位中提取出来河流流速，反演的流速与浮标测量的流速相差0.027 1 m/s.赵丹阳等[68]在黄河流域进行了GNSS-R 机载试验，对镜面反射点处的反射率数据进行了分析.结果表明，当第一菲涅尔反射区落到河流表面的面积越大，GNSS-R 接收功率越强，更加适合河流高度测量.Phuong 等[69]通过地基实验介绍了GNSS 反射计在监测湄公河三角洲水位方面的潜力，研究了河流潮汐测量应用.实验结果表明，同比测量的河流高度和GNSS 反射计测量结果具有良好的一致性，相关性达到了0.85.Li 等[70]分析了河流和地面的CYGNSS 数据，发现河流表面会有更多的相干反射分量，证明了利用GNSS-R 进行河流边界探测的可能性.同年，Warnock 等[71]分析了密西西比州南部帕斯卡古拉河的CYGNSS 反射信号，结果表明，从CYGNSS 得出的河宽测量与观测到的流量高度相关.Zeiger 等[72]利用GNSS 干涉信号在狭窄河流上的不对称潮汐检索水位高度.通过去除Lomb-Scargle 周期图输出中的多峰和输出高度的迭代最小二乘估计以降低GNSS 反射信号中的噪声影响.实验结果表明，测量的河流高度与实际高度相关性可以达到0.99.王峰等[73]从几何构型和理论模型两个角度探究了GNSSIR 提取河流边界和测量河流水位的可行性.他们定义了对河流边界敏感的反-直比和时延变换率两个观测量，通过仿真分析证明了两个观测量对河流边界的敏感性.