基于灰色-神经网络组合模型的纤维混凝土腐蚀劣化预测模型研究

2023-07-31戎泽斌

硅酸盐通报 2023年7期

戎泽斌,王成,2

(1.塔里木大学水利与建筑工程学院,阿拉尔 843300;2.塔里木大学南疆岩土工程研究中心,阿拉尔 843300)

0 引言

随着社会和经济飞速发展,混凝土在工业建筑领域占据着极为重要的地位[1]。混凝土材料虽然具有良好的可施工性,但是也存在低抗裂性、低抗冲击性以及耐久性不佳等缺点[2]。经过诸多学者研究发现,向混凝土中添加适量纤维可以显著提高混凝土的耐久性能。

黄加圣等[3]研究发现,在干湿循环试验作用下,将聚乙烯醇(PVA)纤维添加至混凝土可以提高混凝土的抗盐蚀性能;王洪宇等[4]在室内干湿循环半浸泡作用下进行了不同掺量PVA纤维混凝土的对比试验,结果表明,PVA纤维能够显著提高混凝土的抗干湿循环能力;赵杨等[5]将不同体积掺量的PVA纤维混凝土置于设定侵蚀龄期的硫酸钠溶液中进行对比试验,研究发现,PVA纤维能有效提升混凝土的抗蚀性能。

混凝土耐久性能试验周期长且内容多,时间上存在严重的局限性,因此可以采用模型对混凝土后期的劣化指标进行预测。预测模型主要分为灰度预测法、神经网络预测法和时间序列分析法等。目前学者[6]常采用各种模型对经济、教育等学科进行预测,而针对混凝土耐久性能方面的模型预测成果相对不多。高矗等[7]通过建立灰色(GM(1,1))模型对冻融环境下的混凝土进行抗冻耐久寿命预测,研究发现,该模型能够精准地预测混凝土的寿命;赵明亮等[8]采用反向传播(BP)神经网络模型对混凝土7、28 d的抗压强度进行了预测,结果表明,BP神经网络模型具有很强的非线性映射能力,精准地预测了混凝土的抗压强度。

本文通过开展全浸泡-烘干试验来探究PVA纤维混凝土的抗劣化性能,同时采用GM(1,1)模型、BP神经网络模型和GM(1,1)-BP神经网络组合模型分别对试验数据进行精度评价及预测,研究结果可为纤维混凝土在实际工程中的应用提供科学依据。

1 预测模型及试验方案

1.1 灰色GM(1,1)模型

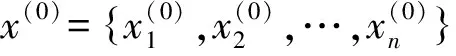
(1)

根据新数列求得平均值数列{zn}并建立灰微分方程,见式(2)。

(2)

GM(1,1)模型微分方程见式(3)。

(3)

a和b为待求参数,假设n取值2和3,代入式(2)并对其移项,变换成矩阵形式,即Xβ=Y,见式(4)。

(4)

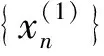
(5)

1.2 BP神经网络模型

神经网络模型(简称ANNs模型)是指仿照脑神经行为并采用分布式并行信息处理的模型[10]。神经网络由大量节点相互连接而成,每单个节点表示一种输出函数,节点与节点间的连接表示权重。本文采取反向传播(BP)神经算法,该算法不但具有多维函数映射性能,而且能够解决隐藏层连接权学习问题。BP神经算法是以网络误差平方为目标函数,采用梯度下降法来计算其最小值。模型的建立主要包含数据收集、设置数据类型、构建网络架构、参数配置、网络训练等多个方面。

传递函数g(x)取Sigmoid函数,见式(6)。

g(x)=1/(1+e-x)

(6)

隐含层输出Hj见式(7)。

(7)

式中:n为输入层的节点个数;wij为输入层节点i到隐含层节点j的权重;xi为输入层节点i的输出值;aj为隐含层节点阈值。

输出层的输出Ok见式(8)。

(8)

式中:l为隐含层的节点个数;wjk为隐含层节点j到输出层节点k的权重;bk为输出层节点阈值。

误差计算公式见式(9)。

(9)

式中:m为输出层的节点个数;Yk为期望输出;Ok为输出层输出,传递函数采用梯度下降法训练。

1.3 GM(1,1)-BP神经网络组合模型

组合预测是指将单种模型进行加权平均,合理赋值模型的加权系数,从而得到高精度线性组合模型[11]。组合计算通常包括方差倒数法、算术平均法、最优权数法三种方法。预测误差是指实际值与预测值之间的差数,预测误差越小,表明精度越高,反之,表明精度低。本文基于有效度原理,并采用算术平均法确定最优加权系数。

预测精度序列Ait见式(10)。

(10)

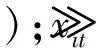
计算预测有效度mi,见式(11)。

mi=(1-σ(Ait))E(Ait)

(11)

式中:σ(Ait)为精度序列均方根误差;E(Ait)为精度序列期望值。

采用算术平均法计算组合系数ki,见式(12)。

(12)

式中:ki为组合系数(i=1,GM(1,1)模型系数;i=2,BP神经网络模型系数)。

确定组合模型预测公式,见式(13)。

(13)

1.4 试验方案

为验证研究模型的精确度,本文通过开展相应的试验对测试数据进行收集,从而将其代入模型进行精度对比,最终选择最优模型。

1.4.1 原材料及配合比

试件制备所用原材料为P·O 42.5普通硅酸盐水泥(阿克苏天山多浪有限公司)、5～20 mm和20～40 mm连续级配卵石、中砂(温宿县同顺砂石料厂)、PVA纤维(12 mm,上海臣启化工科技有限公司)、TXS高性能减水剂(阿拉尔天平建材检测公司)、自来水,配合比见表1。

表1 PVA纤维混凝土试验配合比Table 1 Test mix proportion of PVA fiber concrete

1.4.2 溶液配制

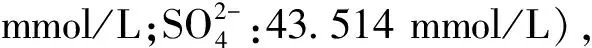
表2 复合盐溶液浓度Table 2 Compound salt solution concentration

1.4.3 试验制度

本试验将PVA体积掺量为0.3%、强度为C30的PVA纤维混凝土试件放入不同浓度复合盐溶液中全浸泡,到达规定时间(10 h)后,将其自然晾干(1 h),然后放入干燥箱中进行烘干(60 ℃),达到设定时间(12 h)后取出试件自然冷却,此过程为1个循环(24 h)。本试验将相对动弹性模量作为混凝土耐久性能宏观评测指标,试验规定每5个循环后对试件进行一次动弹性模量测定,总共30个循环,最后将所测值进行模型预测精度分析。

2 混凝土指标变化及模型预测分析

2.1 混凝土相对动弹性模量变化

不同浓度溶液下混凝土试件评价指标变化如图1所示。由图1可以看出:在经历30次干湿循环后,10倍基准浓度溶液下的混凝土试件相对动弹性模量下降幅度最小,表现最好;其次,混凝土试件抗劣化性能从好到坏依次为5倍基准浓度溶液、基准浓度溶液、清水溶液。

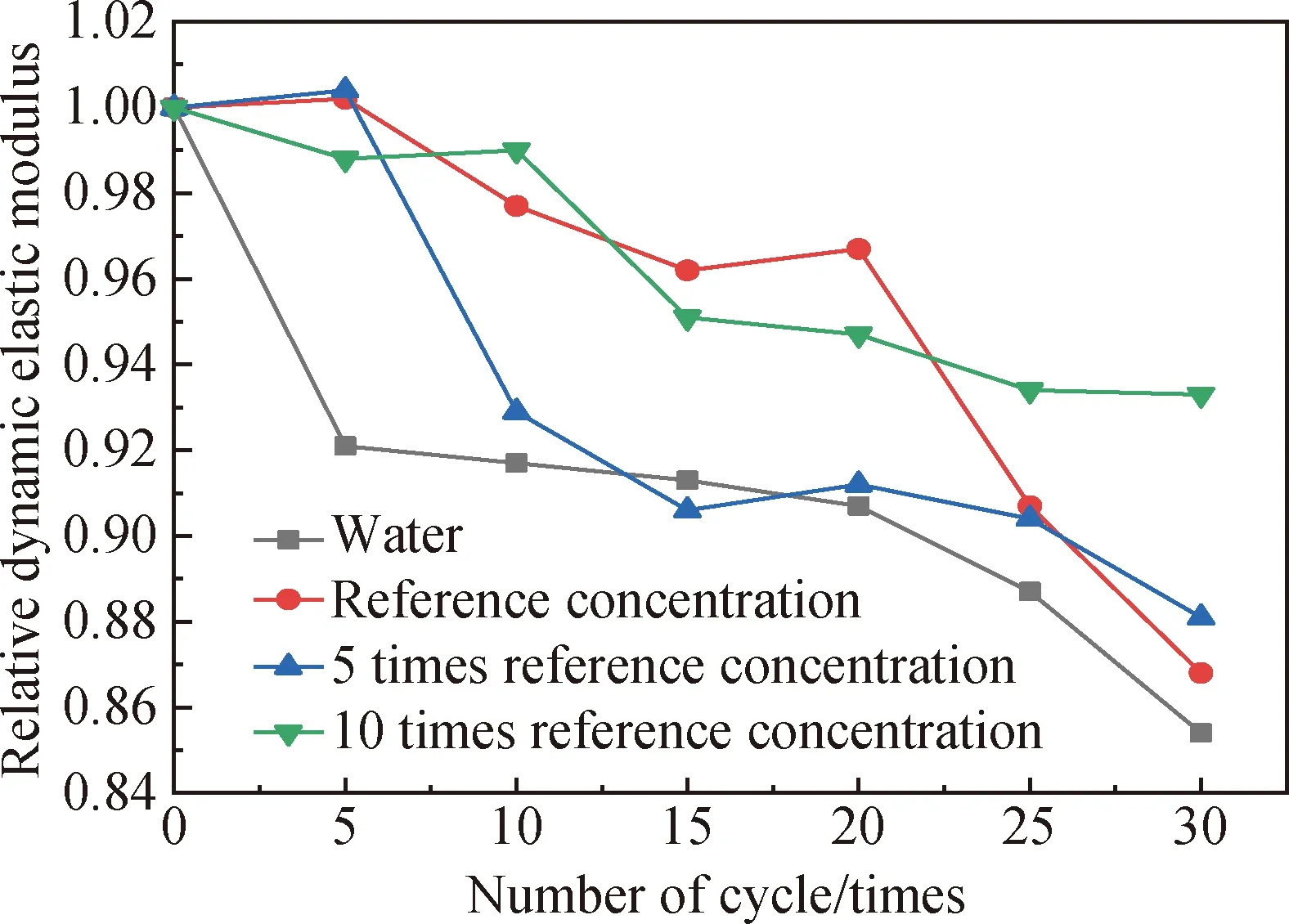
图1 PVA-0.3%混凝土试件在不同浓度溶液下的相对动弹性模量变化Fig.1 Changes of relative dynamic elastic modulus of PVA-0.3% concrete specimens in different concentration of solution

由数据变化趋势可知,在复合盐溶液循环前期和中期时,混凝土试件相对动弹性模量出现上升现象,这是由于在干湿循环作用下,试件内部空隙处被盐蚀产物和水分子所填充,密实性提高,因此相对动弹性模量增大。到了循环后期,试件内部已经没有足够的空间容纳腐蚀产物,因此,基体发生膨胀破坏(基准浓度溶液为循环20次以后,5倍基准浓度溶液为循环25次以后,10倍基准浓度溶液为循环30次以后),故相对动弹性模量下降。

而在清水溶液中,试件相对动弹性模量一直呈下降趋势,这是因为在外部高温作用下,水分子蒸发,混凝土发生水化反应的速率降低,水化产物生成数量不足以填充内部空隙,纤维占据过多空间导致基体内部密实度不足,同时往复循环作用致使混凝土内部裂缝不断扩张,最终基体发生破坏(循环20次以后)。结果表明,复合盐溶液浓度越高,PVA-0.3%试件抗劣化(抗盐蚀)性能越好。

2.2 模型预测步骤及结果

2.2.1 数据选取

首先选取混凝土抗盐蚀试验数据作为参考,其次对模型数据进行格式处理,最后分析预测精度,模型预测所需原始数据见表3。

表3 不同浓度复合盐溶液下PVA-0.3%试件的相对动弹性模量Table 3 Relative dynamic elastic modulus of PVA-0.3% specimens in different concentration of composite salt solution

2.2.2 灰色 GM(1,1)模型

首先,整理并选取预测模型所需数据,随后建立GM(1,1)模型,时间序列长度为7。由于数据样本较少,采用滚动预测,以确保预测准确度。通过将已知数据代入GM(1,1)模型预测0～30次循环后的相对动弹性模量,随后利用0～30次的预测数据来推测35次循环后的预测值(每5次为一个基准点),以此类推,按此方法预测至50次循环。最后对预测数据进行模型精度对比,预测数据见表4。

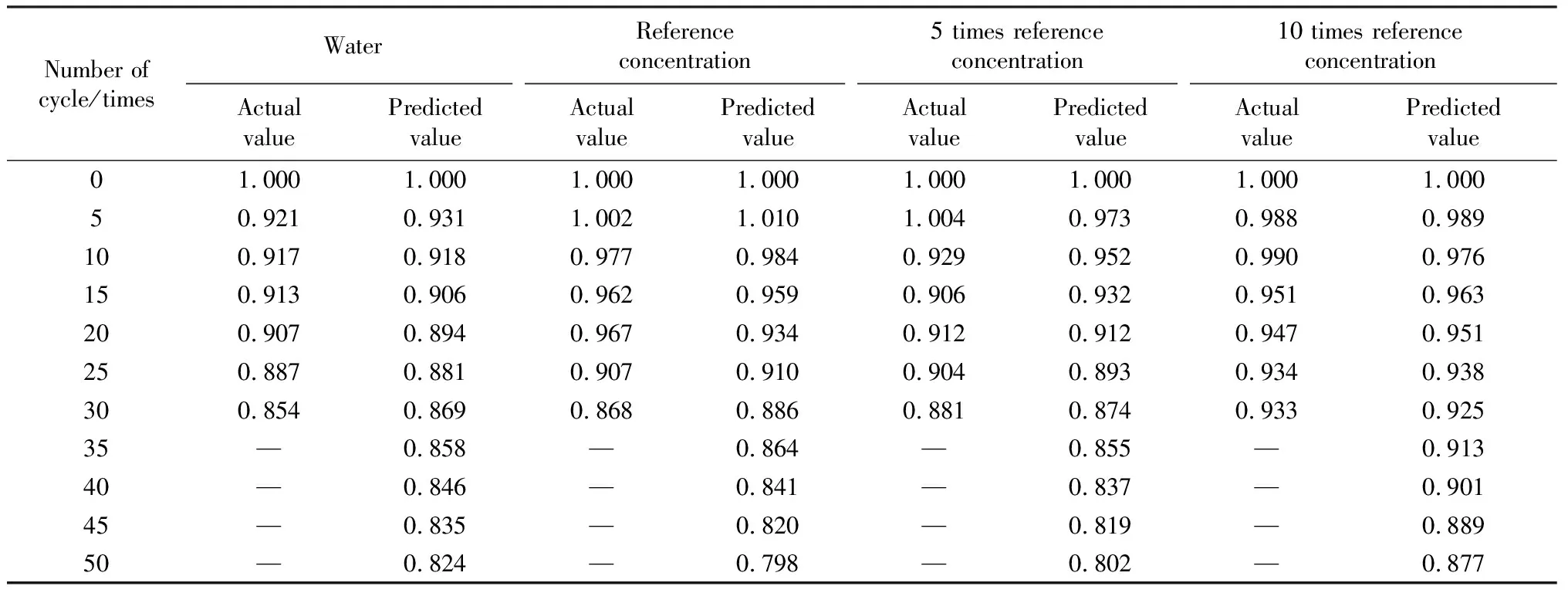
表4 相对动弹性模量实际值与GM(1,1)模型预测值Table 4 Actual values of relative dynamic elastic modulus and predicted values of GM (1,1) model

2.2.3 BP神经网络模型

首先,根据BP神经网络原理确定整体架构,其次,通过整理数据建立模型,最后,将数据代入模型实现预测。由于模型是多输入-单输出方式,因此按照滚动预测方式进行,以此类推,预测至50次循环。模型训练集输入矩阵X和输出矩阵Y分别为

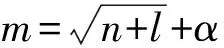
表5 相对动弹性模量实际值与BP神经网络模型预测值Table 5 Actual values of relative dynamic elastic modulus and predicted values of BP neural network model

2.2.4 GM(1,1)-BP神经网络组合模型

分别利用BP神经网络和GM(1,1)模型对混凝土的相对动弹性模量进行预测,之后通过单一模型的占比权重确定最终组合系数k1和k2。将循环次数为0～30次的数据代入式(10)中得到两种模型精度序列。

GM(1,1)模型:

清水溶液:A1t=[1,0.989 2,0.998 1,0.992 3,0.985 6,0.993 2,0.982 7]

基准浓度溶液:A1t=[1,0.992 0,0.992 8,0.996 9,0.965 9,0.996 7,0.979 3]

5倍基准浓度溶液:A1t=[1,0.969 1,0.975 2,0.971 3,1,0.987 8,0.992 1]

10倍基准浓度溶液:A1t=[1,0.999 0,0.985 9,0.987 4,0.995 8,0.995 7,0.991 4]

BP神经网络模型:

清水溶液:A2t=[1,0.998 3,0.998 7,0.999 5,1,0.999 1,0.998 8]

基准浓度溶液:A2t=[1,0.992 9,0.993 7,0.995 5,0.996 6,0.994 4,0.995 6]

5倍基准浓度溶液:A2t=[1,0.994 2,0.990 9,0.998 1,0.996 5,0.997 8,0.994 9]

10倍基准浓度溶液:A2t=[1,1,0.998 9,0.996 9,0.997 4,0.999 9,0.999 4]

将精度序列代入式(11)～(12),计算出组合系数k1、k2值,见表6。

表6 组合模型的k值Table 6 k value of combination model

由表6可以看出,BP神经网络模型的期望值、有效度均大于GM(1,1)模型的期望值,反映出BP神经网络模型的数据集中趋势(稳定性)优于GM(1,1)模型。同时均方差反映了数据的精密程度,均方差越小,精度越高。结果表明,BP神经网络模型的系数占比权重大于GM(1,1)模型的系数,故BP神经网络模型在组合模型中的影响略高。通过确定k1和k2得到组合模型,预测数据见表7。

表7 相对动弹性模量实际值与GM(1,1)-BP神经网络模型预测值Table 7 Actual values of relative dynamic elastic modulus and predicted values of GM (1,1)-BP neural network model

2.3 模型精度分析

为了选取最优精度模型,首先分别计算两种单一模型的混凝土相对动弹性模量预测值,然后通过加权系数组合成新模型,最后计算出组合模型的预测值。同时预测误差反映了模型的精度,它包括相对误差和绝对误差,通常用相对误差来检验预测的准确度,为决策提供可靠的依据。相对误差δ的计算公式见式(14),三种模型的相对误差情况见表8～11。

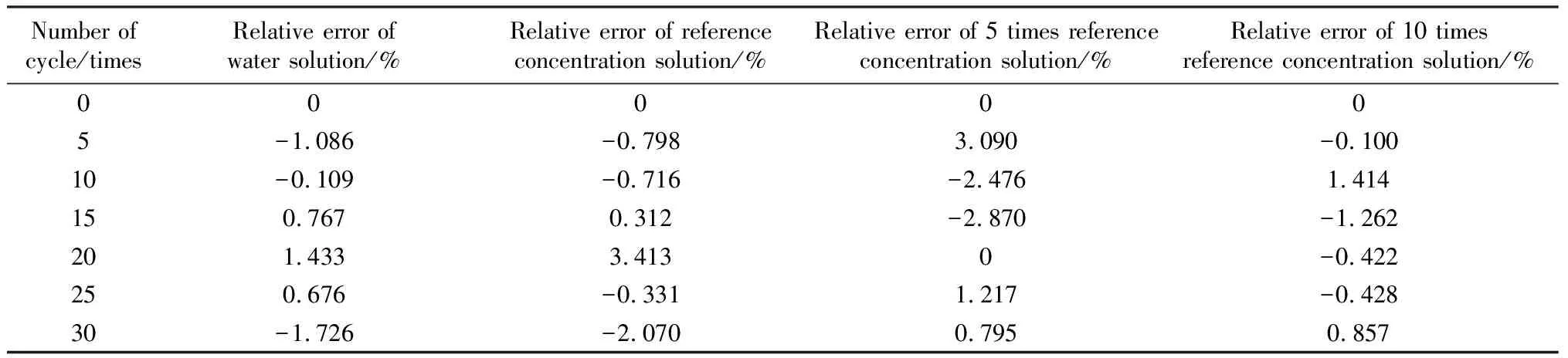
表8 GM(1,1)模型相对误差Table 8 Relative error of GM (1,1) model

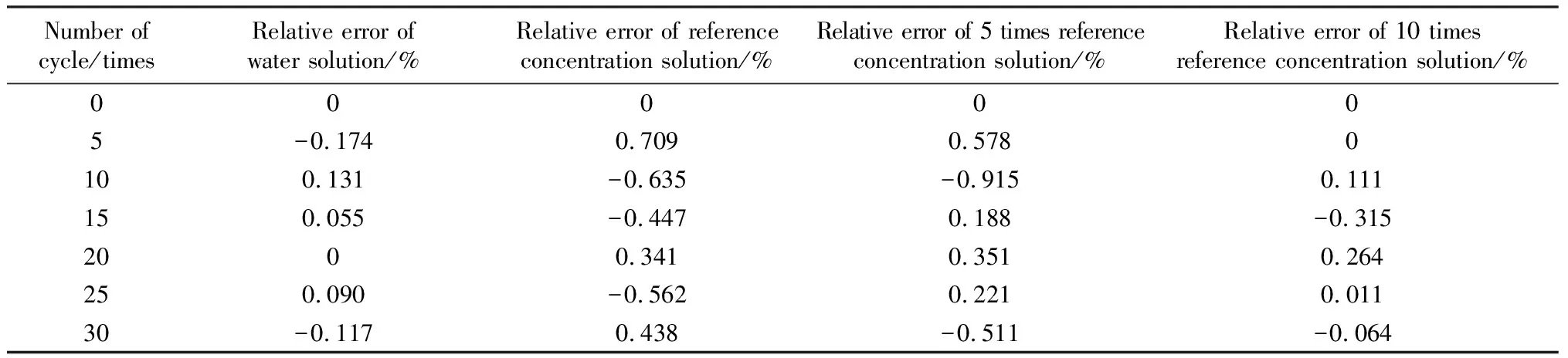
表9 BP神经网络模型相对误差Table 9 BP neural network model relative error

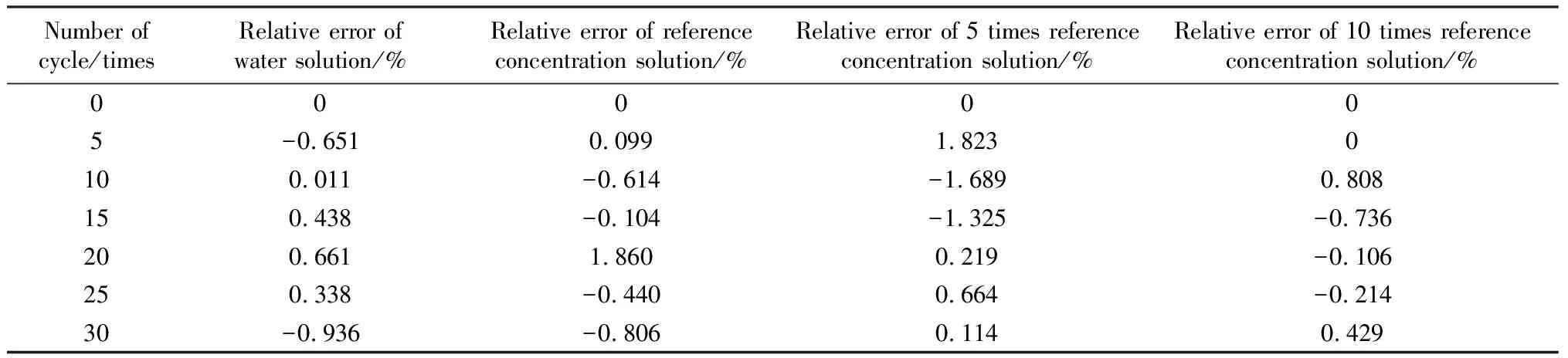
表10 GM(1,1)-BP神经网络模型相对误差Table 10 GM (1,1)-BP neural network model relative error

δ=(Δ/L)×100%

(14)

式中:Δ为绝对误差(测量值-计算值);L为真值(计算值)。

由表8～10可以看出,GM(1,1)模型和BP神经网络模型的相对误差差异较大,其中,BP神经网络模型的精度明显高于GM(1,1)模型。图2为不同浓度溶液下相对动弹性模量真实值与预测值拟合情况。根据图2(a)～(b)可以看出,BP神经网络模型的预测主要是围绕每个测试点数据的趋势来进行拟合,对于整个范围内数据的总体趋势拟合并不显著;而GM(1,1)模型则相反,对整体趋势预测度相对较高,而对单一点变化趋势的拟合效果不明显。因此将两种单一模型进行组合,既能反映单一点的变化趋势,又能反映整体的变化趋势。由表11可以看出,组合模型的误差均值变化最小,表明预测曲线波动幅度小,整体最为稳定。两种单一模型的相对误差最大值均小于4%,表明满足工程精度预测条件。同时,组合模型的误差均方根处于两种单一模型之间,并且变化幅度较小,说明组合模型整体最为稳定,能够最大程度提高混凝土相对动弹性模量的预测精度。

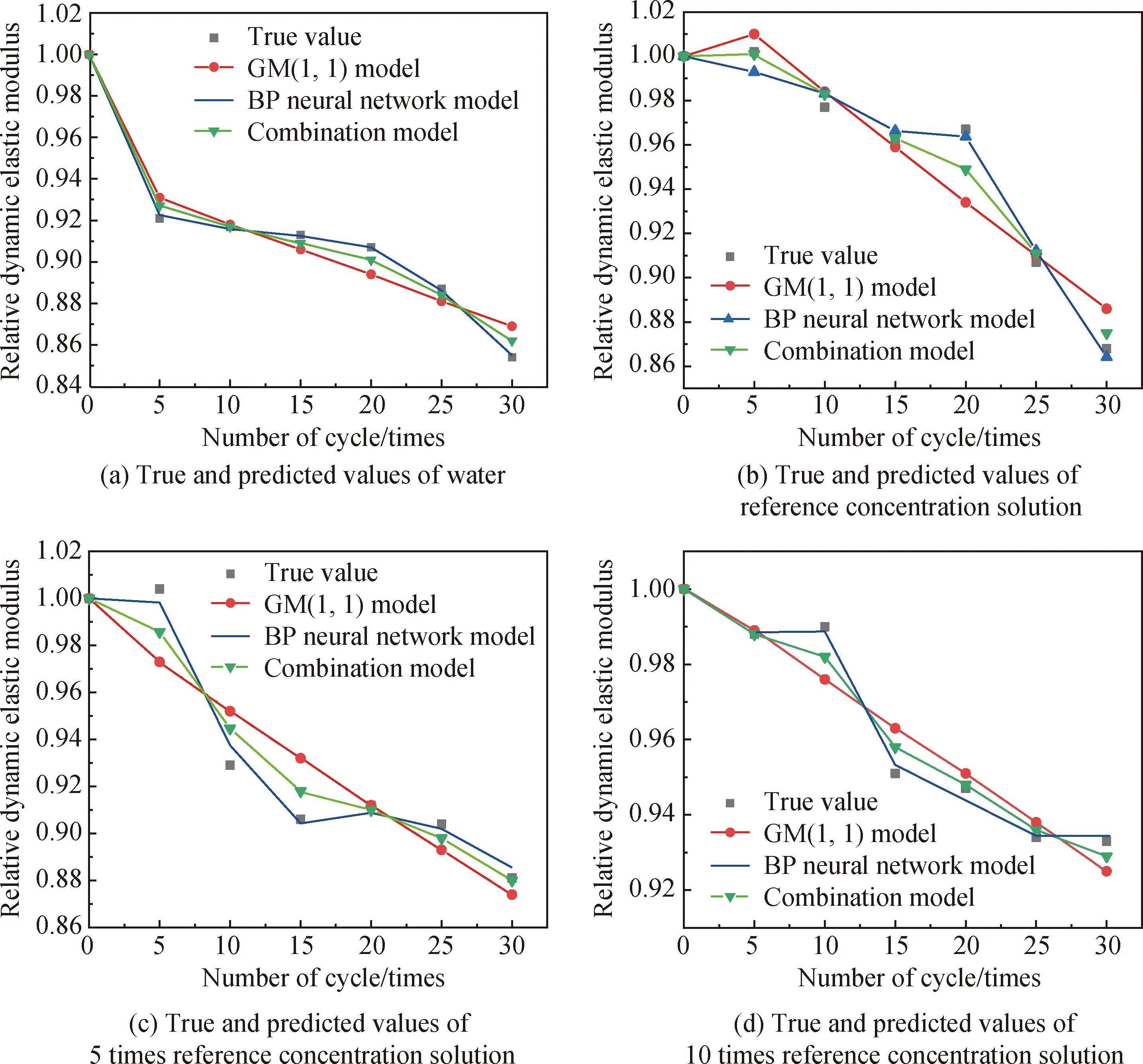
图2 不同浓度溶液下相对动弹性模量真实值与预测值拟合情况Fig.2 Fitting of true value and predicted values of relative dynamic elastic modulus in different concentration solution

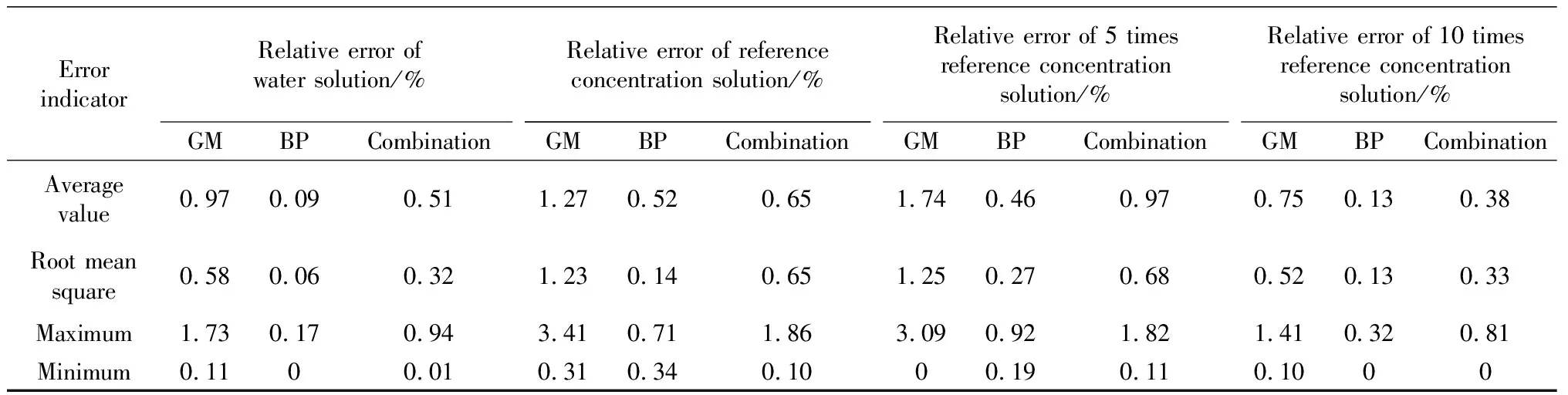
表11 模型相对误差的综合表现Table 11 Comprehensive performance of model relative error

2.4 模型预测结果分析

通过以上分析可知,组合模型的预测输出弥补了GM(1,1)模型和BP神经网络模型的不足之处。为了更好地反映混凝土整体劣化情况,对循环35～50次后的预测数据进行分析,见图3。由图3(a)～(d)可以看出:GM(1,1)模型对数据整体趋势预测较为精准,能较好地反映混凝土劣化指标的变化情况;BP神经网络模型对单个数据的变化趋势预测较为准确,能够较好地反映周期测试点劣化指标的变化趋势;组合模型综合了两种单一模型的预测表现,使数据全局趋势变得更加准确,提高了整体预测效果。

根据劣化试验可知,PVA-0.3%混凝土试件在10倍基准浓度溶液下的抗劣化性能最好。同时通过测试数据可知,模型可以较好地预测混凝土的劣化情况。结果表明,单一模型可以较好地反映出测试精度,而组合模型则综合表现最优。