基于多传感器信息的汽车低速车速估计方法*

浦震峰，唐 亮，上官文斌，王伟玮，蒋开洪

（1.北京林业大学工学院，北京 100083；2.华南理工大学机械与汽车工程学院，广州 510621；3.宁波拓普集团股份有限公司，宁波 315800）

前言

随着智能车辆技术的发展，车辆控制的精细化程度越来越高，高精度的车速信息是实现车辆运动控制的基础。在自动泊车功能中，准确实时的轮速和车速信息可提高车辆位姿估算的准确性［1-2］，实现精准地泊车和减少控制时的超调冲击。然而，受限于泊车系统硬件电子元件的特性和执行机构的性能，泊车算法会限制最高车速。泊车最高车速一般为10 km/h。在泊车过程中，车速经常会低于5 km/h。由于车速过低，轮速传感器发出的脉冲信号间隔时间增长，轮速信号的准确性和实时性大大下降，这会导致车辆位姿估算的精度下降。多普勒雷达、五轮仪等可直接精确测量车速，但是由于成本限制和结构布置等因素，此类设备无法应用于量产汽车。但是随着低速场景下控制需求的增加，利用标准车载传感器进行低速车速估算的需求也在日益增加。

目前车速估计的方法主要有两种。一种是利用轮速传感器信号和惯性测量单元（IMU）信号设计车速估计器，同时利用全球定位系统（GPS）的数据进行校正。但是常规GPS 精度低，传感器信号受环境因素影响大，常出现信号丢失的情况，其可靠性难以满足控制系统的需求［3-4］。Ding等［5］利用全球定位系统、惯性测量单元以及轮毂电机状态信息，设计了面向四轮独立驱动车辆的纵向车速估计算法。另一种是通过传感器信息和建立的车辆动力学模型，设计状态观测器，估算车速。该方法的准确性与所建立的车辆动力学模型密切相关［6］。国内外诸多学者对轮速信号的噪声以及车速估计做了广泛的研究工作。在消除轮速信号的周期性噪声方面，为解决齿圈的非理想等间距所产生的周期性噪声，基于齿圈几何模型和递推约束最小二乘估计算法，Rallo 等［7］提出了一种在线滤波方法，试验证明了该滤波算法不会消除系统本身的速度波动特征信息。对高速行驶时轮速传感器的信噪比降低以及由轮速信号计算数据的发散性等问题，韩宗奇等［8］提出先将轮速信号在频域中进行“滤波”，再通过傅里叶逆变换获得时域下的真实信号。

在基于运动学和动力学的车速估计研究方面，陈浩等［9］利用1阶扩张状态观测器，将车辆纵向动力学方程中的未知非线性部分作为扩张状态进行估计，降低了模型精度对车速估计的影响。Karlsson等［10］以加速度计和陀螺仪测量值为输入，提出了一种基于深度学习卷积神经网络（CNN）的车速估算方法。高振海等［11］基于车辆动力学模型，提出了一种以底盘域传感器信息为输入、基于混合神经网络架构的车速估计算法。Hashemi 等［12］基于卡尔曼滤波器，将LuGre 轮胎模型和车辆动力学相结合，提出了一种车辆纵向车速估计方法。在大加速度工况下，由于车辆模型和轮胎模型会具有很强的非线性，此时经典的卡尔曼滤波器将不再适用，文献［13］～文献［15］中将适用于非线性系统的扩展卡尔曼滤波器和无迹卡尔曼滤波器应用到车速估计中。为避免滤波发散，提高估计精度，周卫琪等［16-17］提出利用最小偏度单形采样策略和遗传算法改进无迹卡尔曼滤波器来减小噪声干扰对车辆状态估计精度的影响。

近年来，随着分布式驱动电动汽车控制技术的发展，针对全轮驱动的分布式驱动电动汽车的纵向车速估计方法已经成为车辆动力学领域的热点问题。高博麟等［18］利用分布式驱动电动汽车的优势设计了基于联邦卡尔曼滤波技术的多方法融合的车速估计方法。赵治国等［19］针对分布式驱动混合动力汽车，利用其后轮毂电机转矩可测和前轮驱动转矩可推算的特点，设计了对噪声方差及均值具有自适应功能的无迹卡尔曼车速估计算法。余卓平等［20］融合运动学和动力学纵向车速估计方法，利用加速度传感器信息和各车轮滑移率反馈值提出了一种纵向车速非线性自适应估计算法。

然而，针对车辆在极低速工况下的车速估计研究则相对较少。目前，用于确定车轮角速度的多是增量编码器类型的传感器［7］，均是以脉冲数为基础计算轮速。当轮速极低时，每单位时间的脉冲数较低甚至为零，除非检测到脉冲，否则无法更新轮速信息。Pino等［21］采用增加霍尔传感器的采样时间以及使用特殊化后的卡尔曼滤波器方法，以减小在低速工况下轮速传感器的量化噪声。中高速工况下的车速估计研究主要是为解决当车轮滑移和侧偏时，车速无法直接通过轮速进行简单计算得到的问题，而低速工况下的车速估计研究主要解决低速工况下，轮速信号精度变低、更新周期变长等因素对车速估算的影响。

综上所述，目前对车速估计算法的研究主要集中在轮速信号的噪声处理以及中高速工况下的车速估算上，关于极低速工况下的车速估计研究较少。为提高低速下车速估算的实时性和准确性，本文针对电驱动汽车提出了一种基于多传感器信息的低速车速估计方法：建立了基于自适应加权融合的轮速算法，提高轮速信息的更新频率；利用电驱动汽车传动系统简单的特点，提出基于电机转速信号的车速估计模型；通过交互多模型融合算法将基于轮速脉冲信号的估计车速和基于电机转速的估计车速进行加权融合，提高车速估计的精度。

1 基于多传感器信息融合的低速车速估计算法

1.1 算法框架

传感器输入的信号有：4个轮速传感器提供4个车轮的轮速脉冲信号Ii，i∈{fl，fr，rl，rr}，转向盘角度传感器提供转向盘转角信号δ，惯性测量单元提供车辆纵向加速度axIMU、侧向加速度ayIMU和车辆横摆角速度信号ωrIMU，驱动电机的旋转变压器提供驱动电机的转速信号nf、nr。

基于测量的信号，建立两个车速估算模型I（基于多轮速脉冲信号的车速估算模型）和模型II（基于电机转速信号的车速估算模型）。

（1）模型I 的估算方法。首先根据转向盘转角δ判断车辆处于直行或是转弯工况。如果是直行工况，则根据各轮速脉冲信号的跳变时刻，将4 个车轮的轮速进行加权融合计算得到更新周期更短的轮速信息。如果是转弯工况，则利用阿克曼转向定理，通过轮速换算以缩短轮速信息的更新周期。最后，基于车辆运动学，利用缩短更新周期后的轮速信息和车辆横摆角速度计算车辆质心处的纵向车速和侧向车速。

（2）模型II 的估算方法。首先根据电机转速信号nf、nr和转向盘转角信号δ，利用整车传动模型计算轮速，再根据车辆运动学模型计算车辆质心处的纵向车速和侧向车速。

（3）基于模型I 估算车速时，可有效地避免噪声干扰，基于模型II估算车速时，求得的车速信息更新周期短、精度高。采用交互多模型融合估计算法（IMM）对两个子模型的估计结果进行加权融合，将两个模型的优势融合到一个组合过滤器中，最终得到较为理想的车速估计结果。

1.2 基于多轮速脉冲信号的车速估算模型（模型I）

1.2.1 轮速计算

霍尔式轮速传感器由齿圈和霍尔传感器组成［19］，霍尔传感器固定在支架上，齿圈随车轮一起转动，在齿圈齿尖靠近或远离霍尔传感器的过程中，传感器内的霍尔元件产生随磁场强度变化的霍尔电压，经电路处理后霍尔传感器输出频率与轮速呈比例的脉冲信号。

工程中常用式（1）计算轮速V[k]：

式中：V[k]为第k个周期时计算的轮速；Nz为齿圈齿数；R0为轮胎有效滚动半径；TN[k-1]为（k-1）周期的时间长度；N[k-1]为（k-1）周期时轮速传感器脉冲信号的个数。

当车速较高时，TN[k-1]的取值为运行周期，固定不变。当车速较低时，单位运行周期TN[k-1]内所能检测到的脉冲数较低或为零，此时由于无法检测到新的脉冲，传统轮速算法会自动切换至周期法，即通过计数器计算一个完整矩形脉冲所经过的时间，并将其赋值给TN[k-1]。这在一定程度上可以提高轮速的计算精度，但同时也会降低轮速的更新频率，其最直观的表现便是轮速曲线中出现非连续的阶梯跳变。

1.2.2 自适应加权轮速算法

为解决单个轮速传感器时轮速更新周期长的问题，本节在传统轮速算法的基础上，通过综合整车4个轮速传感器的轮速脉冲信息，建立自适应加权轮速计算模型。该模型主要面向自动泊车等车辆速度极低且没有大强度的加速或减速的工况，即假设车轮的滑移率均很低可忽略不计。

算法的步骤如下。

（1）利用各轮速脉冲信号Ii，根据式（1）通过周期法计算各轮轮速Vwi。

（2）根据转向盘转角δ判断汽车是转弯还是直行工况。考虑到转向盘的自由行程，设定当转向盘转角的绝对值小于10°时，车辆处于直行工况，否则，车辆处于转弯工况。

（3）在直行工况下，根据轮速信号的脉冲更新时间，计算各轮速信号的权值（可信度），通过自适应加权融合得到更新频率更高、实时性更好的轮速。各轮速信号的权值λi的计算公式为

由于直线行驶时四轮轮速相差很小，通过加权系数将4 个轮速传感器的数据进行融合得到虚拟车速V1，即

式中：λi为各轮轮速信号的权重系数；Vwi为各轮按周期法求得的轮速。

（4）在转弯工况下，根据阿克曼转向原理，利用已知的转向盘转角δ、转向总传动比K、车辆轴距l和轮距S，计算车辆前外轮转角δo和前内轮转角δi。然后根据车辆前内外轮转角和轮距，计算各个车轮的转弯半径，最后通过轮速映射，提高轮速信号的更新频率。

前轮转角的计算公式为

式中φ为前轮平均转角，φ=δ/K。

各个车轮的转弯半径的计算公式为

式中下标fi、fo、ro、ri 分别表示前内轮、前外轮、后外轮及后内轮。

当车辆处于大角度转向时，各个车轮间轮速相差较大，此时选取最小的车轮的轮速Vwi作为虚拟轮速，通过阿克曼转向模型换算剩余车轮的轮速，即当车辆在低速工况下转向时，4 个车轮的轮心绕转向中心点所做圆周运动的角速度相等。因此，各轮轮速间的换算关系为

式中：a、b∈{fi、fo、ro、ri}，其中不计算虚拟轮；Va为待求轮速；Vwb为虚拟轮速；Ra和Rb分别为转向时待求轮和虚拟轮车轮的转弯半径，具体由式（5）求得。

最后，根据运动学模型，通过前轮平均转角φ，前轮轮速Vfi、Vfo，车辆横摆角速度ωr和车辆质心到前轴距离lf计算车辆质心处的纵向车速V1x和侧向车速V1y：

1.3 基于电机转速信号的车速估算模型（模型II）

目前大部分纯电动汽车采用的是单级固定速比减速器的减速方案，整车传动系统中取消了离合器或液力变矩器，这使得通过驱动电机的转速信息进行轮速估计的方法变得更加方便。试验车辆由两个驱动电机分别驱动前后轴。驱动电机与车轮之间通过减速器和差速器传递动力。

当车辆直行时，前轮和后轮轮速为

式中：Vfj、Vrj分别为前轮和后轮轮速；nf、nr分别为前驱动电机和后驱动电机的转速；i0f、i0r分别为前后减速器的减速比。在整车VCU 及电机控制器MCU 的控制下，根据前后电机转速计算所得的前后轮速相差很小，因此可只采用前驱动电机的转速信息进行车速计算。

当车辆转弯时，由于差速器的作用，左右两侧车轮转速ωil、ωir的平均值等于差速器的输入轴转速：

将四轮模型转化为两轮自行车模型后，虚拟前轮轮速Vf可由前差速器输入轴转速求得：

车辆质心处的纵向车速V2x和侧向车速V2y分别为

1.4 基于交互多模型的融合车速估计

基于多轮速传感器脉冲信号的车速估算模型可以有效地避免噪声干扰，但在极低速的情况下，其更新周期变长，而基于电机转速信号的车速估算模型更新周期短，精度高，但传动系统中的齿隙以及电机低速时的转速波动导致车速估计结果存在波动。为充分发挥两个估算模型的优势，本文采用交互多模型融合算法（IMM）对两个车速计算模型的输出结果进行加权融合。交互多模型算法是一种软切换算法，能够对每个子模型的加权因子（模型概率）进行实时调整，从而降低估计误差。完整的算法循环包括输入交互、数据滤波、模型概率更新和输出交互4部分［22］。以纵向车速估计为例，在第k时刻，完整的计算步骤如下。

步骤1：输入交互

将上一时刻（k-1 时刻）数据滤波步骤中模型I和模型II 的卡尔曼滤波器输出的状态估计值、误差协方差Pi(k-1|k-1)，通过模型混合概率μij(k-1|k-1)进行加权融合，并将其作为当前时刻步骤2 中卡尔曼滤波器的状态初值和初始误差协方差P0i(k-1|k-1)，其中i，j为模型序列。本文因只采用了两个模型，故取i，j=1，2。由模型i到模型j的混合概率μij(k-1|k-1)的计算公式为

式中：μi(k-1)为上一时刻在模型概率更新步骤中求得的各模型的模型概率为各模型的归一化常数；p为马尔科夫概率转移矩阵，矩阵元素pij决定了输入交互的作用程度，考虑系统的稳定性和准确性，最终，p取为

若为第一次循环（k=1），则模型概率μi(k-1)、状态估计值和误差协方差P0i(k-1|k-1)均取初值：

步骤2：数据滤波

利用卡尔曼滤波器分别对两个车速估算模型进行数据滤波。

模型Ⅰ的卡尔曼滤波器：利用惯性测量单元的纵向加速度信号axIMU与由模型Ⅰ计算所得的纵向车速信号V1x通过卡尔曼滤波器进行滤波。考虑道路坡度对纵向加速度信号的影响，实际的车辆纵向加速度为

式中：g为重力加速度；i为道路坡度，实际行驶过程中坡度变化缓慢，可以认为道路坡度i对时间的导数为零。因此，可建立微分方程组：

将其离散化，得到：

式中Δt为程序运行周期。

将纵向车速vx和道路坡度i作为状态变量，将式（17）转化为状态空间方程的形式：

式中：xk为状态变量；zk为系统测量值；uk为系统输入；wk为系统过程噪声；vk为测量噪声，它们是均值为零且相互独立的高斯白噪声，各自的协方差矩阵分别为Q、R；系统矩阵A、控制矩阵B和观测矩阵H分别为

卡尔曼滤波器主要包含时间更新和测量更新两个过程［19］。

模型Ⅱ的卡尔曼滤波器：将基于电机转速信号的车速估算模型（模型Ⅱ）求得的纵向车速V2x作为卡尔曼滤波器的测量值zk；将axIMU作为卡尔曼滤波器的系统输入uk；系统矩阵、控制矩阵和观测矩阵均与模型Ⅰ中的对应矩阵相同。经时间更新和测量更新后得到模型II中纵向车速和道路坡度的最优状态估计和误差协方差P2(k|k)。

步骤3：模型概率更新

交互多模型算法最终是将步骤2 中两个滤波器的状态估计结果进行加权融合。利用极大似然函数Λi(k)计算每个模型的模型概率μi(k)：

步骤4：输出交互

侧向车速也采用交互多模型融合估计方法，具体步骤和纵向车速估计相似，不同的是在数据滤波步骤中，采用一维卡尔曼滤波器将模型i得到的Viy、与加速度信号ayIMU进行融合滤波。设置滤波器的状态变量为vy，系统输入为ayIMU，观测值为Viy。系统矩阵A和观测矩阵H均设为1，控制矩阵B的取值设为Δt。经交互多模型融合估计后得到侧向车速的估计结果VyIMM。最终估计得到的车辆合速度VIMM为

2 车速估计算法的验证

2.1 试验场地及试验设备

为检测所提出算法的实时性与有效性，本文进行了实车试验。在不同路面上进行低速直行和低速转弯以验证算法的可靠性，试验场景如图1 所示，其中测试路面包括平坦路面、鹅卵石路面和坡度为18%的坡道。

图1 实车试验场景

实车试验平台如图2 所示，试验采用一辆双电机四驱SUV 作为试验车辆，该车配备有基础的底盘域传感器，即包括轮速传感器、惯性测量单元、转向盘角度传感器、挡位传感器等。其中惯性单元固定在靠近车辆质心，用于测量车辆纵向加速度、侧向加速度以及横摆角速度。同时，该车还装备有VBox数据采集系统（非接触式汽车测试仪），其可通过高精度GPS 信号精确地测量车辆的实际速度，用于验证车速估计算法的准确性。惯性测量单元信号和4 个轮速传感器信号通过线束与控制器连接，电机转速信号和转向盘角度信号通过整车CAN 网络输出给控制器和数据采集系统。同时，控制器输出的车速估计结果也可通过CAN 网络输出，最后利用数据采集系统和计算机采集并记录试验数据。试验车辆详细参数如表1所示。

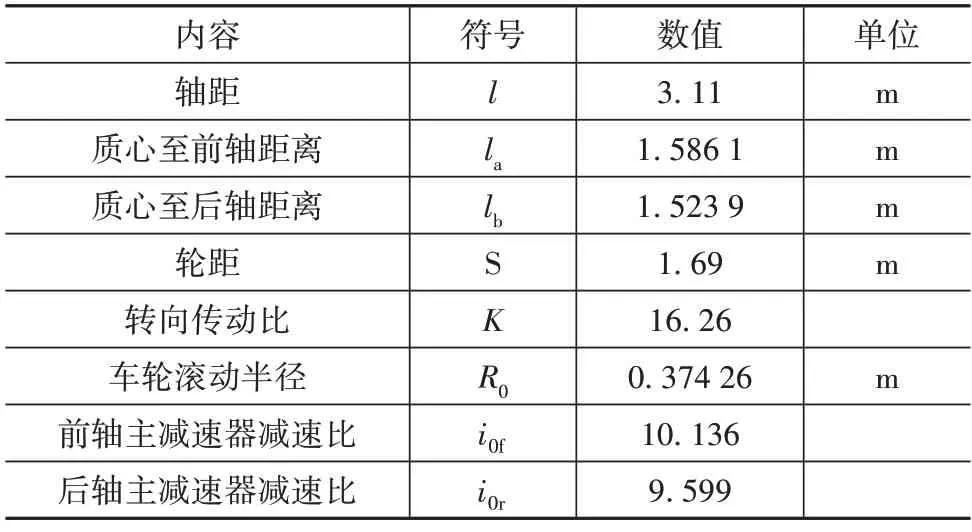
表1 车辆结构参数

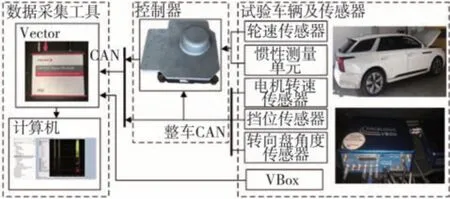
图2 实车试验平台

2.2 试验结果

在典型的低速行驶工况下，对所提出的低速车速估计算法进行验证。将VBox所测得的车辆合速度作为用来参考的实际车速，并将传统ESP算法输出的车速估计结果和本文所提出的基于多传感器信息融合的低速车速估计算法输出的车速估计结果进行对比。试验工况包括在平坦路面下的低速直行和低速转弯工况以及在复杂路面和坡道上的低速直行工况。

本文中用于对比的ESP算法采用了一种基于传感器信号融合的级联观测器系统进行车速估计［23］。该车速观测器系统由底层、中层和上层组成。底层为低通滤波器，用于滤去传感器的部分噪声，得到转向盘转角、车轮轮速、纵向和侧向加速度以及制动管路压力等信号；中间层基于滤波后的传感器信号估算道路坡度、制动力矩并根据上层估计得到的纵向和侧向车速估算车轮滑移率和侧滑角；上层则进行路面附着系数估计、轮胎力估计、通过车辆动力学估算车辆的纵向、侧向加速度，通过纵向车速估计器和侧向车速估计器融合轮速及加速度传感器信号得到纵向和侧向车速，并最终获得车辆的合速度。

2.2.1 平坦路面下的试验结果

在平坦路面下低速直行试验中，车辆由静止起步。试验结果如图3 所示。由图可见：当车辆刚开始起步时，由于采用的是周期法计算轮速，ESP 算法输出的车速曲线呈现出明显的阶梯状；而本文中提出的车速估计算法融合了更新周期更短的电机转速信息，在车辆起步阶段可以得到更加准确实时的车速估计结果。

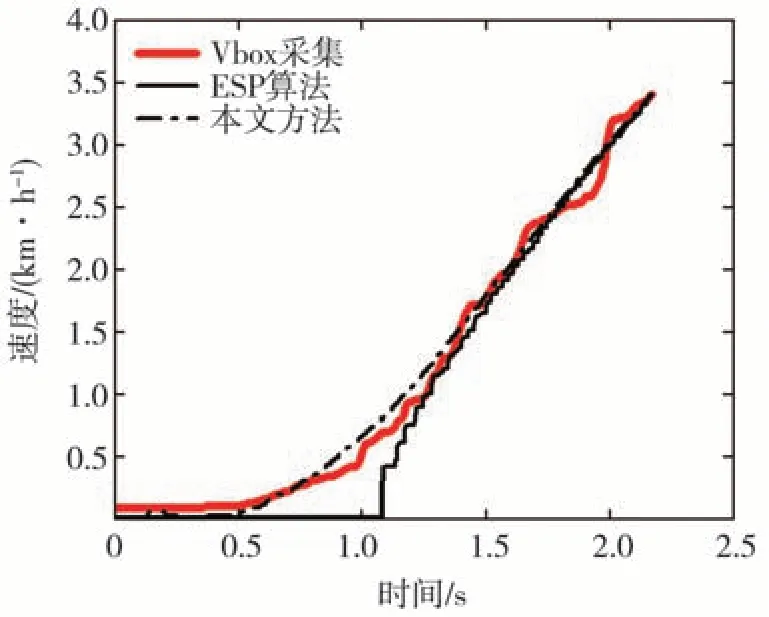
图3 平坦路面下低速直行试验结果

在平坦路面下低速转弯试验中，车辆由静止起步，驾驶员施加的转向盘转角曲线如图4 所示，向左转向时转向盘转角为负，向右转向时转向盘转角为正。速度曲线如图5 所示。在8 s 左右时车辆开始减速，此时由于检测不到新的轮速脉冲，传统ESP算法的车速曲线会出现短暂的延迟，而本文提出的算法的车速曲线能够快速地跟踪实际车速的变化。但是，在4 和9 s 左右，当转向盘转角最大时，估算的车速与实际车速间出现较大的误差。这是由于实际车辆转向系统的非线性特性，即实际的转向总传动比K并非恒定值，由转向盘转角计算前轮转角时出现误差，导致车速估算结果出现偏差。

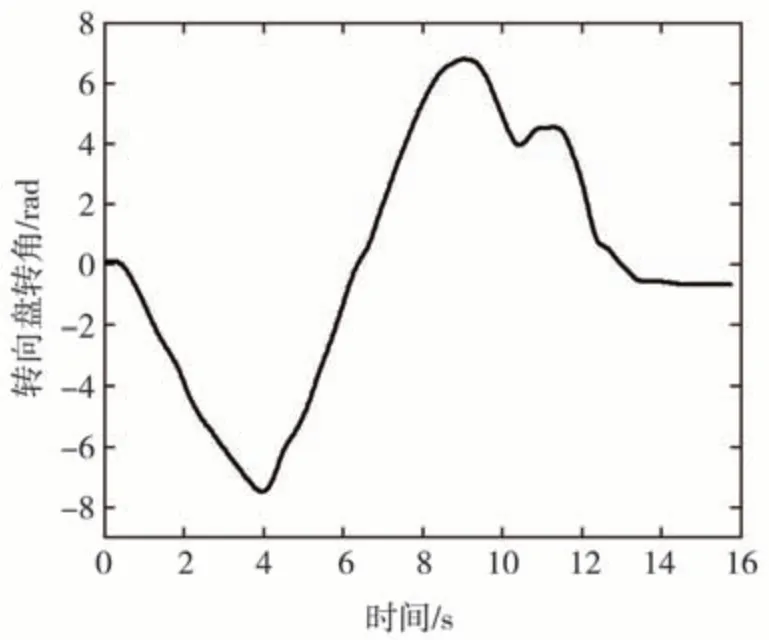
图4 转向盘转角曲线

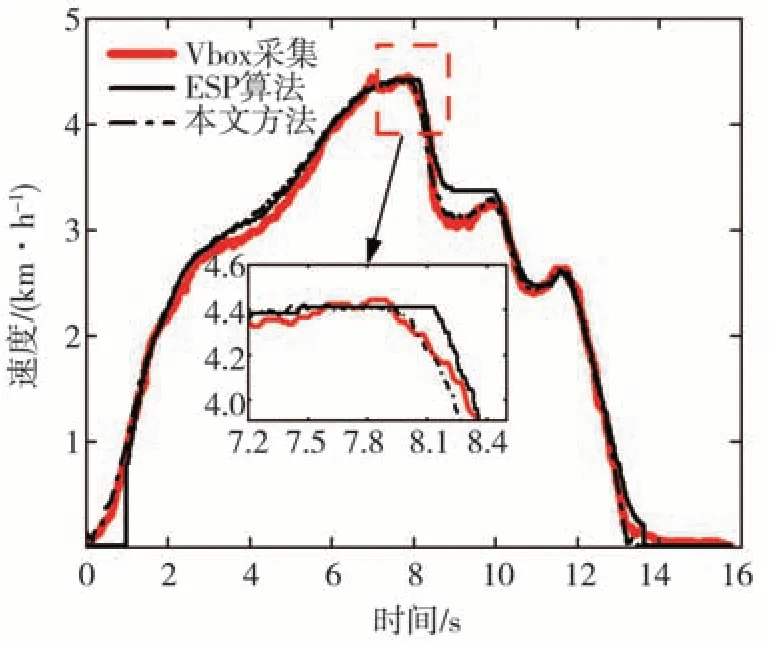
图5 平坦路面下低速转弯试验结果

2.2.2 复杂路面下的试验结果

在复杂路面下的低速直行工况试验中，选用鹅卵石路面作为复杂路面，试验结果如图6 所示。同其他试验工况类似，起步时，ESP 输出的车速曲线存在较大的延迟，并且由于路面颠簸，车速曲线出现较大波动。得益于卡尔曼滤波器的滤波作用，本文提出的算法的车速曲线波动较小，输出的车速曲线相对更加平稳。但是由于并未考虑车辆在颠簸路面上的俯仰和侧倾运动对加速度信号的影响，故本文方法估算出的车速与实际车速之间仍有一定的偏差。

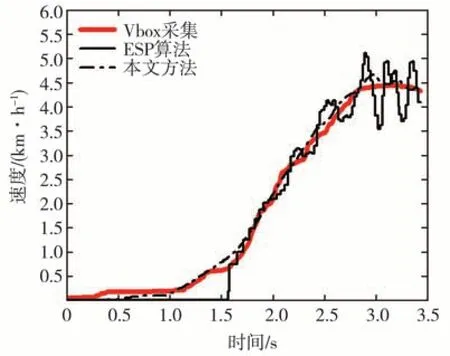
图6 复杂路面下低速直行

2.2.3 坡道上的试验结果

当车辆处于坡道上时，受重力影响，惯性单元所测得的加速度与车辆的实际加速度之间存在偏差，因此，获得道路的坡道对进行车速估计具有重要的作用。道路坡度的估算结果如图7 所示，车速的估计结果如图8所示。

图7 坡度估计结果

图8 坡道上低速直行试验结果

如图8（a）所示，当车速达到0.7 km/h 时，ESP 算法输出的车速曲线才会出现变化，而本文提出的算法可以实时更新车速变化，其所能检测到的最低车速远小于0.7 km/h。图8（b）为模型I、模型II以及本文利用融合算法将两个模型加权融合最终输出的车速结果对比。低速工况下，由于驱动电机转速信号的波动，模型II 输出的车速估计曲线也呈现出一定的波动。基于轮速脉冲信号的模型I 的车速估计结果则不存在这种波动噪声，但是其更新周期长，存在阶梯形的量化噪声。本文提出的车速估计算法将两个模型的估计结果加权融合，在缩短车速更新周期的同时减小了电机转速信号的波动噪声对车速估计的影响，最终得到更加精准的车速估计结果。由于当车辆处于坡道上时，难以使车辆保持在相对恒定的低速状态，故车速曲线波动较大，同时加速度信号受车辆俯仰的影响也变大，导致坡度估算出现一定的偏差，车速估算结果也受到一定的影响。

为了将本文提出的算法和传统ESP 算法的估计精度进行定量比较，分别计算两种算法所输出的车速结果相对于VBox 测量值的平均绝对误差（MAE）ς：

式中：yi为由VBox 所得的测量值为算法输出的估计值；n为在一次实车测试中数据采样点的个数。表2 列出了在不同测试场景下，传统ESP 算法和本文提出的算法所输出车速信息的MAE指标。

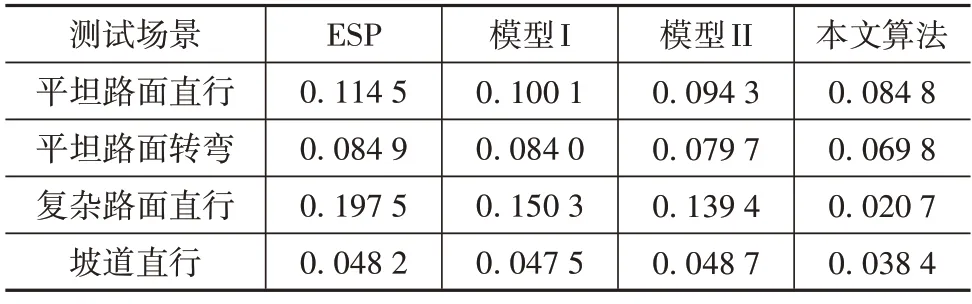
表2 ESP和本文算法所输出车速信息的MAE指标

由表2 可以看出，采用融合算法后的估计结果比单一方法的估计结果精度更高，并且本文提出的算法的车速估计结果在各种不同测试场景下的MAE 指标均比传统ESP 算法有所提升，这表明该算法在典型的低速场景下可以得到更加精确稳定的车速估计结果。

3 结论

针对电驱动汽车，本文以低速工况下的车速估计方法为研究对象，利用轮速传感器脉冲信号和电机转速信号建立了两个车速子估计器模型，通过交互多模型融合算法充分发挥两个子估计器模型各自的优势。通过实车试验得出以下结论：

（1）引入驱动电机的转速信号进行车速估算可以降低低速工况下由轮速传感器的增量式传感器特性所产生的阶梯形量化噪声，并且可以大大降低车辆起步时为等待轮速脉冲所产生的车速更新延迟。

（2）针对驱动电机的转速信号在低速工况下出现波动对车速估计产生影响的问题，将基于多轮速脉冲信号的车速估算模型与基于电机转速信号的车速估算模型的计算结果进行加权融合，由此减小电机转速信号波动和轮速脉冲信号更新周期长对车速估计精度的影响，从而实现更加精确实时的低速车速估计。

对于通过离合器或液力变矩器进行切断和传递动力的传统集中动力式车辆，当车辆处于低速时，离合器或液力变矩器常处于未完全接合状态，此时无法准确地通过动力源（发动机）转速估算轮速，本文中模型II 的估计精度将会因此下降，导致最终融合估计结果的精度降低。后续将讨论采用无级变速系统（CVT）的车辆在低速工况下的车速估计方法。