基于改进混合A*的智能汽车时空联合规划方法*

胡 杰，张志豪，陈瑞楠，陈锐鹏，刘昊岩，朱 琪，陈 晖

（1.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉 430070；2.武汉理工大学，汽车零部件技术湖北省协同创新中心，武汉 430070；3.武汉理工大学，新能源与智能网联汽车湖北省工程技术中心，武汉 430070；4.东风汽车股份有限公司商品研发院，武汉 430000）

前言

运动规划模块作为自动驾驶系统的关键组成部分，其主要任务是基于地图、感知和定位等信息生成一条安全、高效和舒适的可行驶轨迹［1］。当前智能汽车已在低速、简单道路场景下实现落地，但在中高速的复杂动态场景下，由于规划方法问题导致智能汽车的行驶表现还有所欠缺。

根据是否进行时空解耦，轨迹规划方法可分为时空解耦规划和时空联合规划。时空解耦规划将三维的轨迹规划解耦为二维的路径规划和一维的速度规划［2-3］，其核心思想是首先考虑静态障碍物规划一条可行驶路径，然后在路径的基础上考虑动态障碍物进行速度规划。常用时空解耦规划方法有采样法、搜索法和数值优化方法［4］等。这种先求解路径再求解速度的规划方式，可以显著降低轨迹求解的难度，实现轨迹规划在线高效求解。但由于轨迹在路径与速度层面存在强耦合，时空解耦顺序求解的方式极大限制了所生成轨迹的灵活性和适应性，只能处理静态绕障、路口让行等纵横向运动较为解耦的一般场景［5-6］，在换道超车、邻车切入等多目标复杂动态场景下容易陷入轨迹次优［7］，制约了当前智能汽车的实际运行表现。

时空联合规划直接在三维时空范围内求解可行驶轨迹，相比时空解耦规划，尽管由于问题维度增加导致求解效率降低，但这种时空联合同时求解的规划方法具有更大的求解空间和求解灵活性，在各类场景下具有更接近于熟练驾驶员的表现。目前时空联合规划方法主要可分为基于采样［8］、基于搜索［9］和基于数值优化［10］的3 种方法。与时空解耦规划方法存在的问题相似，单一基于采样或搜索的时空联合规划方法难以平衡轨迹的求解质量和求解耗时，单一基于数值优化的时空联合规划方法在三维时空范围内建模难度大，最优解收敛速度慢且易陷入局部最优［6，11］。因此有研究者提出将采样或搜索方法与数值优化方法相结合的时空联合规划方法。

文献［11］中提出了一种基于搜索和优化结合的时空联合规划方法，首先引入三维时空栅格地图对车辆的运动环境进行建模，然后在三维栅格地图中使用A*搜索自定义的车辆动作空间获得初始轨迹，最后使用模型预测控制的方法对初始轨迹进行平滑处理。但该方法对车辆的实际可行驶状态空间简化过多，导致轨迹完备性和轨迹质量很差。文献［6］中采用RRT*在时空范围内进行采样获得初始轨迹，然后使用数值优化的方法对初始轨迹进行平滑后处理。但RRT*的搜索鲁棒性和一致性较差，导致相邻周期之间的轨迹不连续，无法满足结构化道路上对轨迹求解质量和实时性的要求。文献［7］中首先获取时空范围内的初始轨迹作为参考轨迹，然后基于参考轨迹构建梯形棱柱体时空走廊，在可行驶走廊内使用分段贝塞尔曲线进行轨迹优化获得精细轨迹，但其没有提出具体的初始轨迹计算方法。

综上，针对传统时空解耦规划方法在多目标复杂动态场景下易陷入轨迹次优，而现有时空联合规划方法难以平衡轨迹求解质量和求解耗时的问题。为此，本文提出了一种采用分层架构的智能汽车时空联合规划方法，首先使用改进混合A*在三维时空范围内进行轨迹粗搜索获得初始轨迹，通过合理设计混合A*的节点扩展方式以及启发函数和代价函数，提升轨迹的直接搜索效率和行为的合理性，然后基于初始轨迹构建安全可行驶时空走廊，并综合考虑车辆动力学约束、路径及速度连续性约束等条件，构建以安全、舒适和高效为优化目标的数值优化模型对初始轨迹进行平滑后处理获得最终轨迹。

本文中首先介绍时空轨迹粗搜索过程，然后介绍时空轨迹后处理过程，最后进行仿真分析，验证所提规划方法相较于传统时空解耦规划方法具有更高的灵活性和规划结果合理性，同时验证所提方法计算的实时性。

1 时空轨迹粗搜索

时空轨迹粗搜索包括两个步骤。第一步，构建时空栅格地图，以描述未来一段时间内自车与障碍物的位置关系及相对运动关系。第二步，基于时空栅格地图使用改进的混合A*直接搜索初始粗轨迹。为提高轨迹搜索效率，本文基于轨迹的时空属性提出了一种新的子节点扩展方法，并通过合理设计启发函数和代价函数对可行驶节点进行代价排序，避免了节点沿着不必要的方向进行无效拓展。

1.1 时空栅格地图构建

二维x-y栅格地图只具有几何属性，因此传统混合A*［12］无法直接搜索带有时间属性的可行驶轨迹。轨迹的直接搜索需要构建三维x-y-t栅格地图，考虑到本文研究场景为具有车道线指引的结构化道路，为降低运动建模的难度，本文使用Frenet 坐标系进行统一的场景描述［13］，构建三维s-l-t时空栅格地图。其中s表示沿道路指引线的纵向位置，l表示相对于道路指引线的横向位置，t表示时间。首先构建二维s-l栅格地图，然后将二维栅格地图沿离散化的时间轴t进行扩展，离散时间间隔为Δt，得到离散形式的三维s-l-t时空栅格地图，如图1所示。

图1 时空栅格地图

在三维s-l-t时空栅格地图中，静止物体表现为沿时间轴t占据相同的s-l区域，如图1绿色部分所示；移动物体在不同时间点的s-l位置状态如图1 蓝色和黄色部分所示，表现为倾斜向上。其中动态障碍物在未来一段时间内的位置应由预测模块［14］给出。因此相较于二维栅格地图，使用时空栅格地图可以清晰地描述未来一段时间内自车与障碍物的位置关系及相对运动关系。

1.2 时空节点扩展

1.2.1 时空节点状态空间表示

传统混合A*的节点状态空间为（s，l，θ，d），其中(s，l)表示车辆的纵向位置和横向位置，θ表示航向角，d表示车辆前进或后退行驶方向，相邻节点之间保持空间状态连续，节点扩展方式如图2（a）所示。

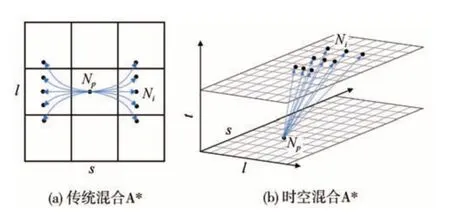
图2 传统混合A*与时空混合A*节点扩展方式对比

本文提出的三维时空混合A*节点状态空间增加了时间维度信息，同时考虑到结构化道路行车过程中不允许倒车，因此时空混合A*对应的车辆状态空间为（s，l，θ，v，t）。其中前3 项与传统混合A*相同，第4 项v为速度状态量，第5 项t为节点相对于当前自车位置所在节点的时间，定义规划时域T表示一次规划考虑的未来时间范围，则节点的相对时间t取值范围为[0，T]。

1.2.2 时空子节点扩展过程

基于时空节点的状态空间特征，本文采用前轮转角δ和加速度a作为具有非完整性约束车辆的控制变量，基于如图3 所示的车辆运动学模型进行子节点扩展，节点扩展方式如图2（b）所示，时空子节点扩展过程如下。

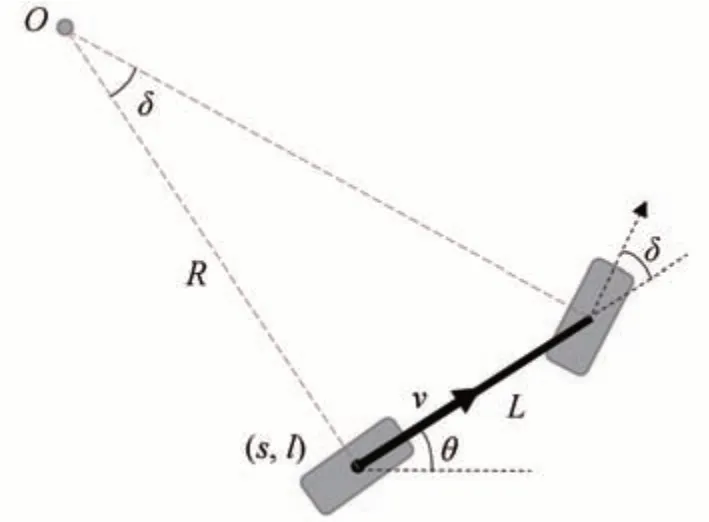
图3 车辆运动学模型

（1）离散前轮转角δ和加速度a

基于车辆运动学约束将前轮转角δ在[-δmax，δmax]进行均匀离散化，为保证子节点的扩展能够沿着车辆航向角方向进行，前轮转角离散数量N需要选取为奇数，得到离散前轮转角集Δ，表达式如下：

式中i=1，2，…，N。

为平衡节点的扩展效率和扩展质量，采用变间隔离散化车辆加速度a，离散加速度分布以0 为基准，基于车辆动力学参数确定加速度上下限[-amax，amax]，在[-amax，amax]区间内向左右两侧以逐渐加大的间隔采样加速度，得到离散加速度集A，表达式如下：

（2）基于运动学模型的时空子节点扩展

传统混合A*采用固定步长的方式扩展节点，如图2（a）所示，轨迹搜索效果受搜索步长的影响很大，搜索步长过小将降低搜索效率，步长过大将降低搜索结果质量。本文所提出的时空混合A*基于加速度采样获得空间变步长，如图2（b）所示，从每个父节点NP(sp，lp，θp，vp，tp)开始，基于前述离散前轮转角δ和加速度a和进行子节点扩展，子节点Ni(si，li，θi，vi，ti)的时空扩展过程表示如下：

式中：L为车辆轴距；dt为相邻节点的时间步长；ai∈A；δi∈Δ。

为保证子节点与障碍物安全无碰撞，将上述时间步长dt按照更小的时间步长tstep均匀划分为M段，则基于式（3）可获得由父节向子节点扩展过程中的一组中间过渡节点[Ni1，Ni2...NiM]。若子节点及中间过渡节点与障碍物均无碰撞发生，则认为该子节点安全。此外，对子节点还应进行道路边界约束检查，以确保子节点处于道路边界内。若子节点同时通过碰撞检查和道路边界约束检查，则进行下一步的节点代价评估，否则丢弃该扩展节点。

遍历离散前轮转角集Δ 和离散加速度集A，即可基于父节点扩展得到一系列子节点。

1.3 时空节点启发函数设计

合适的启发函数可以引导混合A*的搜索沿着最接近目标点的方向进行。传统混合A*多采用A*搜索结果和Reeds-Sheep 曲线作为启发式函数，选择两者的最大值作为最终启发信息。但使用A*和Reeds-Sheep 曲线作为启发函数存在耗时严重的问题［15］，因此传统混合A*一般应用于对于算法计算实时性要求不高的低速非结构化场景，无法满足实时性要求较高的复杂动态场景。

本文研究对象为具有明确指引线的结构化道路，并基于Frenet 坐标系进行环境和运动建模，因此道路的几何形状对混合A*搜索过程的影响很小，同时考虑到在线求解的实时性，因此可以使用当前点到目标点的距离作为启发项。本文采用时空欧式距离作为混合A*粗搜索过程的启发函数，满足条件的子节点Ni(si，li，θi，vi，ti)启发函数Hi计算如下：

式中：第1 项为平面欧式距离启发项；sgoal、lgoal分别为目标节点的纵向位置和横向位置；第2 项为时间距离启发项；tgoal为目标节点对应的相对时间，作用于避免混合A*陷入不必要的时间停滞，加快搜索过程；wH1和wH2分别为对应启发项的权重。

1.4 时空节点代价函数设计

子节点代价指从搜索起始节点到当前节点Ni(si，li，θi，vi，ti)的累积代价，由父节点NP的代 价Gp、父节点Np与子节点Ni之间的过渡代价两部分组成，可表示为

式中：Gi为子节点舒适性代价项，通过子节点与车道中心线(scenterline，lcenterline)的横向偏移衡量（式（6））；Gp为父节点代价；wg1、wg2、wg3为权重系数；Ei为子节点目标代价项，通过子节点的速度与期望车速vexpected的偏差衡量（式（7））；Si为子节点安全性代价项，节点与障碍物的相对距离可以衡量碰撞风险。

为提高混合A*节点搜索的高效性和轨迹行为的拟人性，本文参照文献［16］中在时空栅格地图中建立风险场，该理论将障碍物视为风险源中心，给予障碍物周围的节点赋予不同的碰撞风险惩罚值，风险场方向由风险源中心向四周辐射，自车与风险源中心距离越近则碰撞风险越大，反之，碰撞风险越小。风险场分布模型表达式为

式中：(s，l)和(us，ul)分别表示节点和障碍物风险源中心的位置坐标；σsg和σlg分别表示障碍物在s向和l向的分布因子，分布因子与障碍物的轮廓以及障碍物在s向和l向的速度和加速度相关。

结构化道路行车过程中，静态障碍物的风险场分布具有各向同性，动态障碍物的风险场分布具有各向异性，相应的基于风险场的子节点安全代价值可表示为

式中：r为节点相对风险源中心的位置向量；θr为向量r与障碍物速度v之间的夹角，由于静态障碍物的风险场具有各向同性，因此其θr始终为0。

1.5 时空混合A*算法流程

以当前自车所在位置（s1，l1，θ1，v1，t1）为搜索起始节点Nstart，基于式（3）进行时空节点扩展，扩展过程中综合考虑节点无碰撞和道路边界约束进行节点合理性检查，并基于式（4）和式（5）进行节点代价评估以寻找最优扩展节点，直至搜索至目标节点Nend，完成时空混合A*搜索过程，得到由离散节点表示的初始粗轨迹。算法流程如表1所示。

表1 时空混合A*算法伪代码

2 时空轨迹后处理

基于改进混合A*直接搜索出的轨迹不够平滑，无法满足控制模块跟踪执行的需要，故本文采用数值优化的方法对初始轨迹进行平滑后处理。所提时空轨迹后处理方案分为两步：第一步，创建可行驶时空走廊，三维时空范围的移动障碍物将导致自车可行驶区域严重非凸，因此本文引入可行驶时空走廊［13］将自车与周围障碍物分离开，以构建优化问题的凸可行集，保证轨迹优化后处理过程的实时性；第二步，创建轨迹优化模型，在可行驶时空走廊内，综合考虑车辆动力学约束、路径及速度连续性约束等条件，构造以安全、舒适和高效为优化目标的轨迹优化模型，求解优化模型获得最终轨迹。

2.1 可行驶时空走廊创建

上述轨迹粗搜索过程获得的离散轨迹点时空分布较为稀疏，需要减小相邻轨迹点之间的间隔以便于控制执行。本文利用前述节点扩展过程中获得的一系列严格无碰撞且符合车辆运动学约束的中间过渡节点进行轨迹等价重构，获得一组由扩展节点Ni及其对应的中间过渡节点[Ni1，Ni2，...，NiM]构成的时空节点集Λ，节点个数为Nc，Λ表达式为

沿时空节点集Λ表示的轨迹铺设可行驶时空走廊，具体过程如下。

从当前自车所在位置对应的节点P1(s1，l1，θ1，v1，t1)开始，获取相对时间t1时刻障碍物及道路边界的空间占据状态。使用有向矩形框描述t1时刻的自车及障碍物实际外轮廓，如图4 所示，并沿坐标系的s向和l向构建自车有向矩形框的最小包络框。

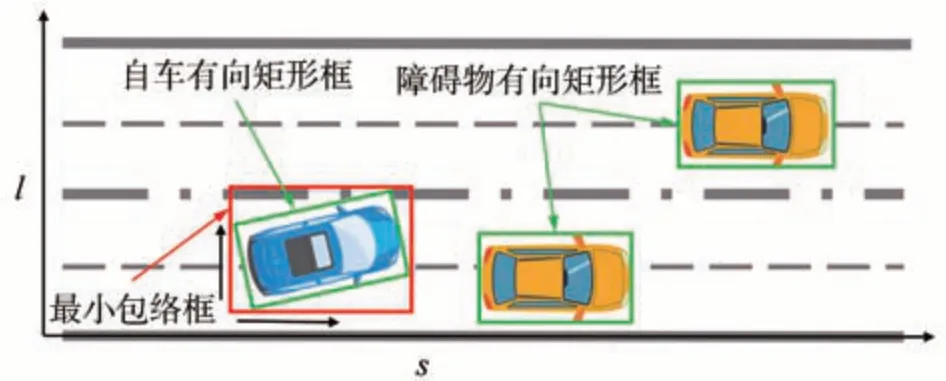
图4 t时刻自车及障碍物的矩形框表示

如图5 所示，以连续的扩展量 Δs，沿d方向顺序对上述最小包络框进行增量式膨胀，其中增量式膨胀过程如图5 序号1，2，…，10 所示。当某一方向的膨胀与障碍物发生碰撞、超出道路边界或累计膨胀量达到设定上限时，终止该方向膨胀并记录此时该方向上的累计膨胀量Id，直至4 个方向全部扩展结束。基于累计膨胀量Id，可以确定t1时刻节点在s和l方向的上下边界限值，如式（11）所示。

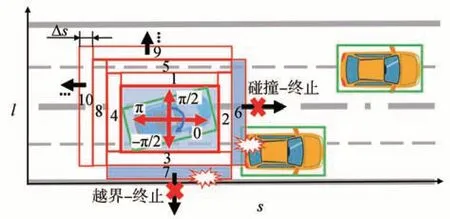
图5 t时刻节点可行驶走廊开辟过程

由上述最小包络框的扩展过程可知，节点在上述边界限值内可以确保严格无碰撞，因此基于边界限值可构造该节点的可行驶走廊。以相同的方式对时空节点集Λ中剩余节点Pj(sj，lj，θj，vj，tj) 依次执行上述过程，完成可行驶时空走廊的开辟过程。

2.2 轨迹优化模型构建

优化模型的目标函数定义如式（12）所示，由Jl和Js两部分构成。目标函数第1 项为轨迹点相对于初始粗轨迹的偏离惩罚项，第2 项为轨迹点的横纵向速度与期望速度的偏差惩罚项，第3项和第4项分别为轨迹点的横纵向加速度和加速度变化率惩罚项，目标函数Jl的第5 项为轨迹点相对于车道中心线的偏离惩罚项。

基于前述可行驶时空走廊计算出的节点边界限值，构造轨迹点边界安全性约束为

考虑车辆动力学约束，构造轨迹点横向和纵向速度、加速度约束为

为保证轨迹的高阶连续性，本文参照文献［17］中所提出的分段加速度变化率优化理论，使用常量加速度变化率连接相邻两点，则轨迹点横向的连续性约束可表示为

式中j=1，…，Nc-1。

上述目标函数是二次函数，约束条件为线性约束，因此可将上述数值优化模型转化为经典的二次规划问题，求解二次规划问题获得最终轨迹。

3 仿真分析

为充分验证本文所提时空联合规划方法的有效性和优越性，搭建MALTAB/SimuLink 和PreScan、CarSim 联合仿真平台，在换道超车和旁车切入两类典型复杂动态场景下进行实验验证，如图6所示。

图6 联合仿真平台

规划时域T选取为8 s；障碍物轨迹预测时长Tp应与规划时域T一致［14］，故Tp=8 s。本文假设障碍物轨迹预测结果为已知；本文规划轨迹的跟踪控制采用常用的LQR 算法和PID 算法。实验其它相关参数见表2。

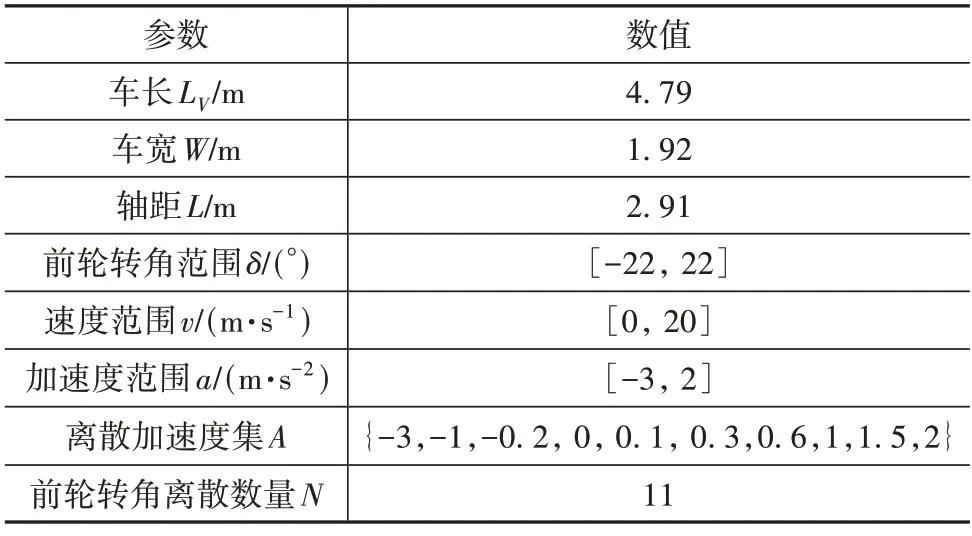
表2 仿真实验相关参数

3.1 换道超车场景

如图7 和图8 所示，初始状态自车位置为（5 m，1.75 m），纵向速度vs(0)=15.0 m/s，纵向加速度as(0)=0 m/s2，横向速度和加速度均为0。自车行驶方向前方有一辆低速移动的同向行驶障碍物车辆V1 影响自车正常通行，相邻车道有一辆对向行驶障碍物车辆V2，为获得满意的驾驶空间，自车需要进行换道以超越前方障碍物车辆。根据障碍物不同的分布情况和运动状态，换道超车场景可分为以下两类。

图7 换道超车场景一

（1）换道超车场景一

车辆V1 从初始位置（30 m，1.75 m）处以5 m/s的车速做匀速直线运动，车辆V2从初始位置（110 m，5.25 m）处以-10 m/s的车速做匀速直线运动。

图9和图10展示了本文所提方法在换道超车过程中的完整行驶轨迹。t=1.13 s 时，由于车辆V2距离自车较远，综合考虑通行效率和碰撞风险，自车选择进行换道并适当加速以超越前车V1；t=3.71 s时，自车超越前车V1，此时由于车辆V2 驶近碰撞风险增大，自车选择并回原车道；t=4.96 s 时，完成并道；此后车速逐渐降低至期望车速15 m/s，完成换道超车。图11 展示了本方法在其中一个规划周期的轨迹规划结果对比。可以看出，本方法在轨迹粗搜索阶段得到的路径、速度和加速度不够平滑，经过时空轨迹后处理过程可以有效提升规划路径和速度、加速度的质量，同时严格符合车辆动力学约束，有利于控制模块进行轨迹跟踪。

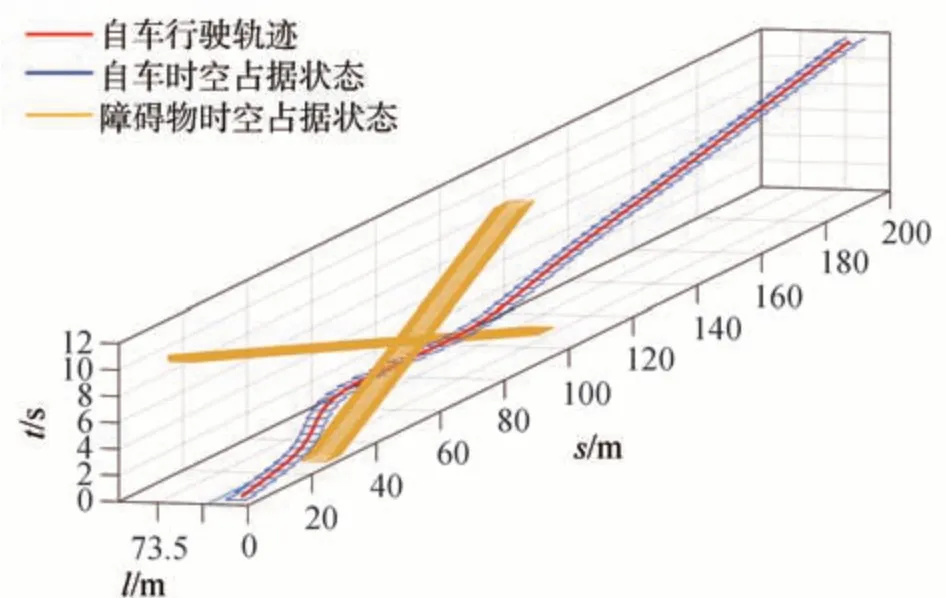
图9 换道超车过程三维行驶轨迹（场景一）

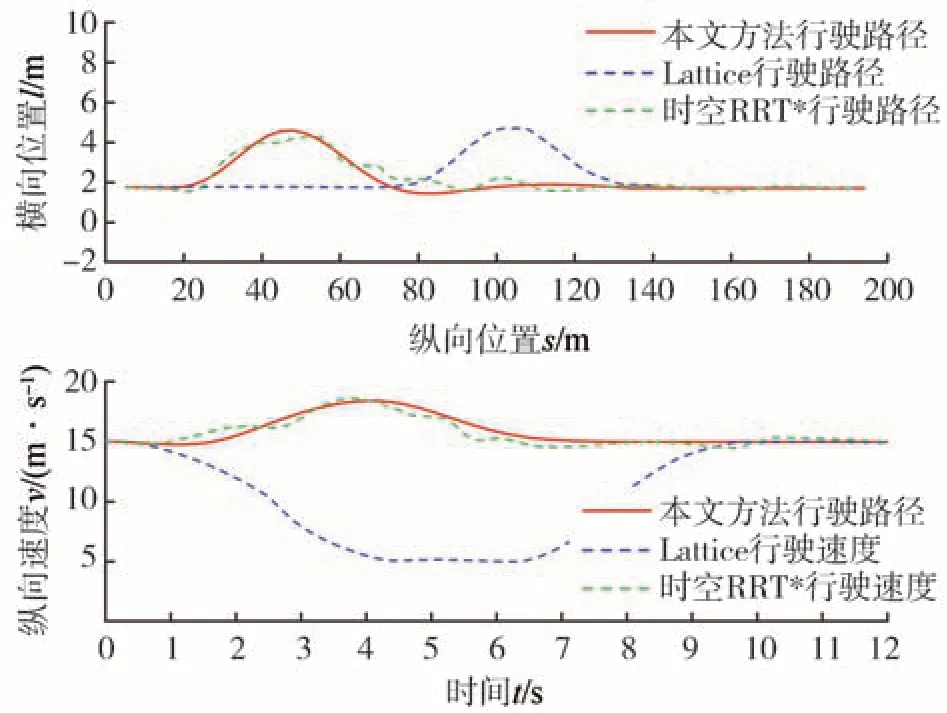
图10 换道超车过程不同规划方法对比（场景一）

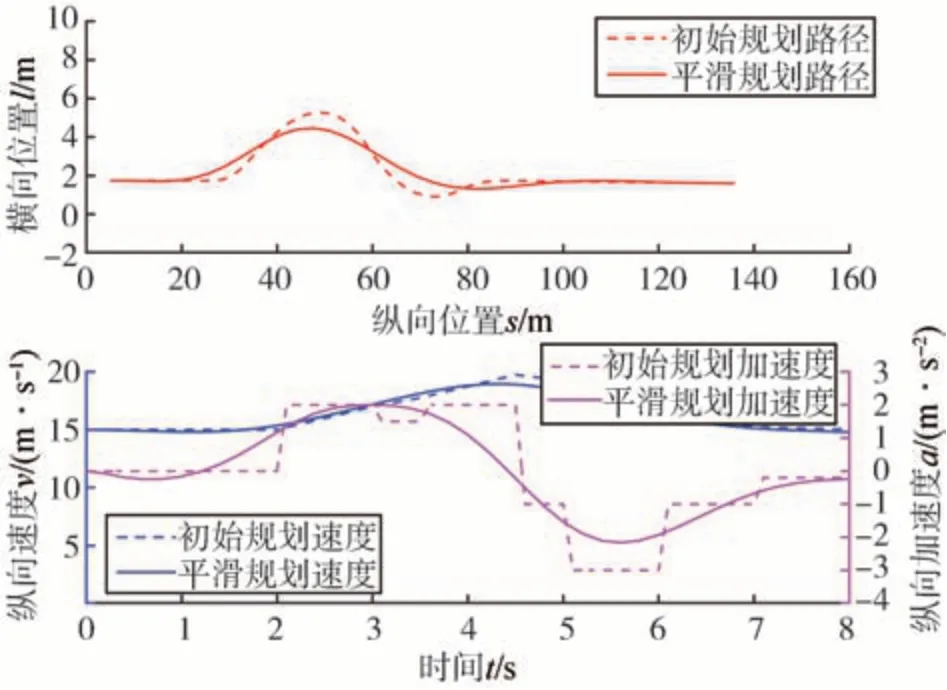
图11 换道超车路径及速度、加速度规划结果（场景一）

图10 还展示了另外两种对比方法在换道超车过程中的车辆行驶轨迹。蓝色曲线为传统解耦规划方法Lattice［18］，自车选择减速跟随低速运动的前车V1 行驶，在相邻车道车辆V2 完全驶离后再进行换道超车。相比本文所提方法，Lattice 方法的行为过于保守，降低了自车通行效率。这是因为解耦的方法分别由路径规划和速度规划处理静态和动态障碍物，然后合并路径和速度的求解结果生成轨迹。这种解耦处理的方式极大地限制了轨迹的求解空间和求解灵活性，导致复杂动态场景下容易出现轨迹次优。绿色曲线为前言部分所述时空联合规划方法［6］时空RRT*，轨迹行为表现与本方法相近，灵活性相较Lattice均有明显提升，这是由于时空RRT*与本方法的可行驶轨迹求解空间近似。但其在相邻规划周期之间的轨迹连续性很差，车辆行驶路径和速度频繁抖动，原因在于时空RRT*本质上仍是一种随机采样方法，导致轨迹规划结果的不确定度很高。本文所提方法在三维时空范围内统一处理障碍物，具有更加完备的轨迹求解空间。同时采用基于搜索的时空混合A*进行轨迹直接求解，在提升求解灵活性的同时，有效兼顾了相邻周期之间轨迹的连续性，因此行为表现更加灵活，结果更加合理。

（2）换道超车场景二

车辆V1 从初始位置（25 m，1.75 m）处以5 m/s的车速做匀速直线运动；车辆V2从初始位置（40 m，5.25 m）处以-10 m/s 的初始车速做变加速直线运动。

仿真结果如图12 和图13 所示，初始时刻由于相邻车道的车辆V2距离自车较近且车速较高，综合考虑碰撞风险和通行效率，自车适当减速避让前车V1；t=1.45 s 时，旁车V2 开始逐渐驶离，自车选择换道并适当加速以超越前车V1；t=2.93 s 时，超越前车V1，自车选择并回原车道，同时车速逐渐降低，在t=4.62 s 时完成并道，换道超车完成。图13 蓝色曲线Lattice 与本文所提方法的行为表现相近，但本文所提方法的换道开始时间更早，速度波动更小，具有更高的通行效率和乘坐舒适性。图13 绿色曲线所示为时空RRT* 行驶轨迹，同样存在由于周期之间轨迹连续性差导致的行驶抖动问题。图14 展示了本文方法在轨迹平滑后处理前后的路径及速度、加速度的规划结果对比。

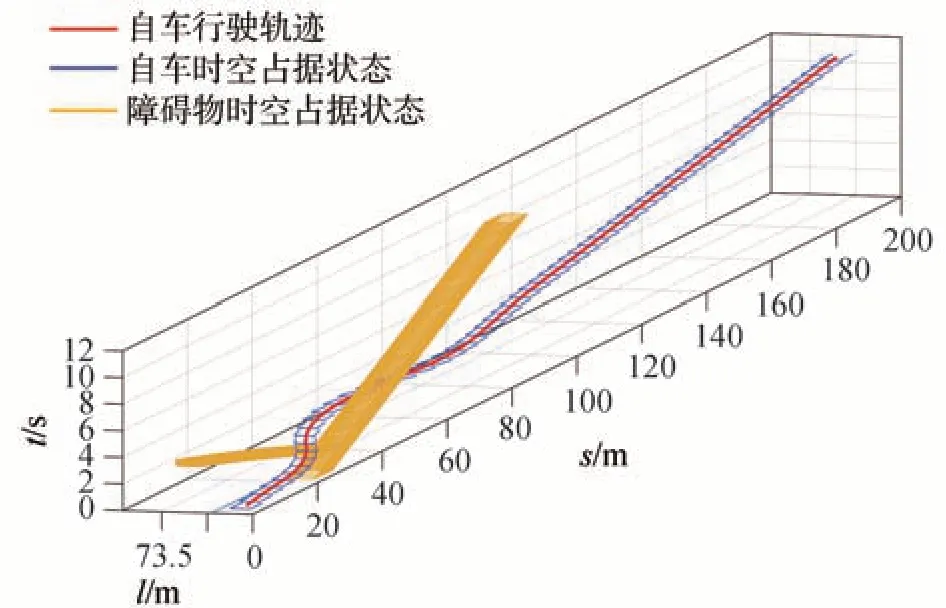
图12 换道超车过程三维行驶轨迹（场景二）

图13 换道超车过程不同规划方法对比（场景二）

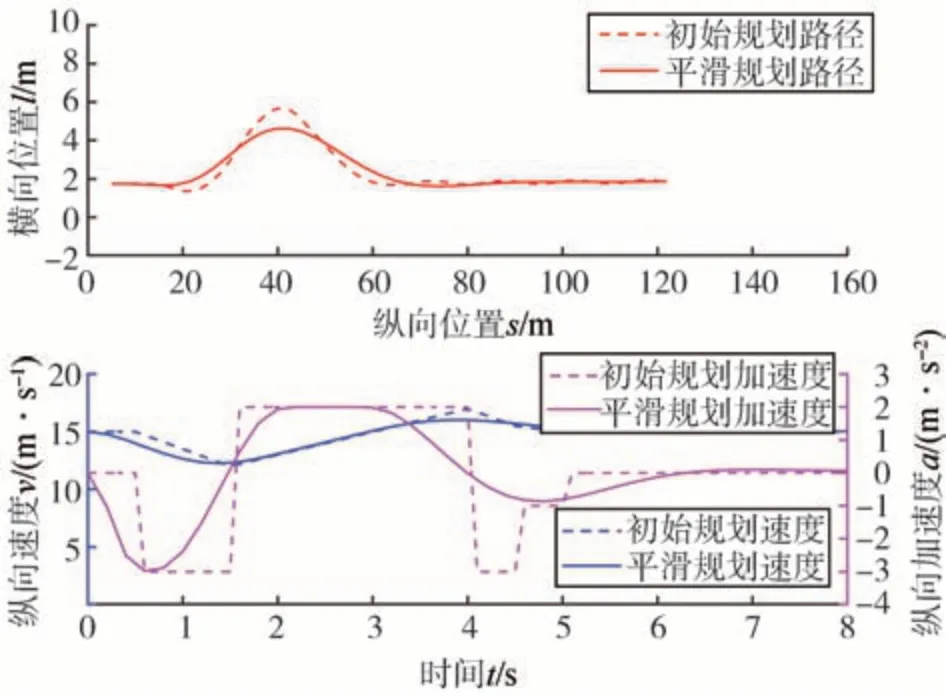
图14 换道超车路径及速度、加速度规划结果（场景二）

3.2 旁车切入场景

如图15和图16所示，初始状态自车位置为（5 m，1.75 m），纵向速度vs(0)=15.0 m/s，纵向加速度as(0)=0，横向速度和加速度均为0。自车相邻车道上有两辆同向行驶的障碍物车辆V1 和V2，由于车辆V2 行驶车速较低，车辆V1 选择切入自车所在车道以寻求超越车辆V2。根据障碍物不同的分布情况和运动状态，旁车切入场景主要可分为以下两类，如图15和图16所示。

图15 旁车切入场景一

图16 旁车切入场景二

（1）旁车切入场景一

车辆V1 从初始位置（30 m，5.25 m）处以5 m/s的车速匀速切入自车车道；障碍物车辆V2从初始位置（90 m，5.25 m）处以15 m/s的车速匀速运动。

图17 和图18 展示了本文所提方法在旁车切入自车车道过程中的完整行驶轨迹。由于旁车V1 切入车速较低，综合考虑通行效率和碰撞风险，t=2.23 s 时，自车选择纵向加速以超越切入车辆V1，同时在车辆V1 切入点附近向右进行轻微避让以降低碰撞风险。值得说明的是，这种横纵向联合处理横向方向上突然出现障碍物的行为与人类驾驶员的驾驶习惯是一致的。t=5.47 s 时，超越车辆V1 完成，自车返回车道线附近居中行驶，同时车速逐渐降低到期望车速。

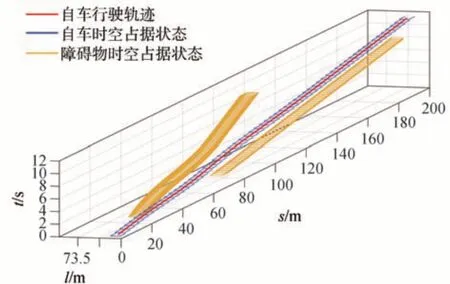
图17 旁车切入过程三维行驶轨迹（场景一）

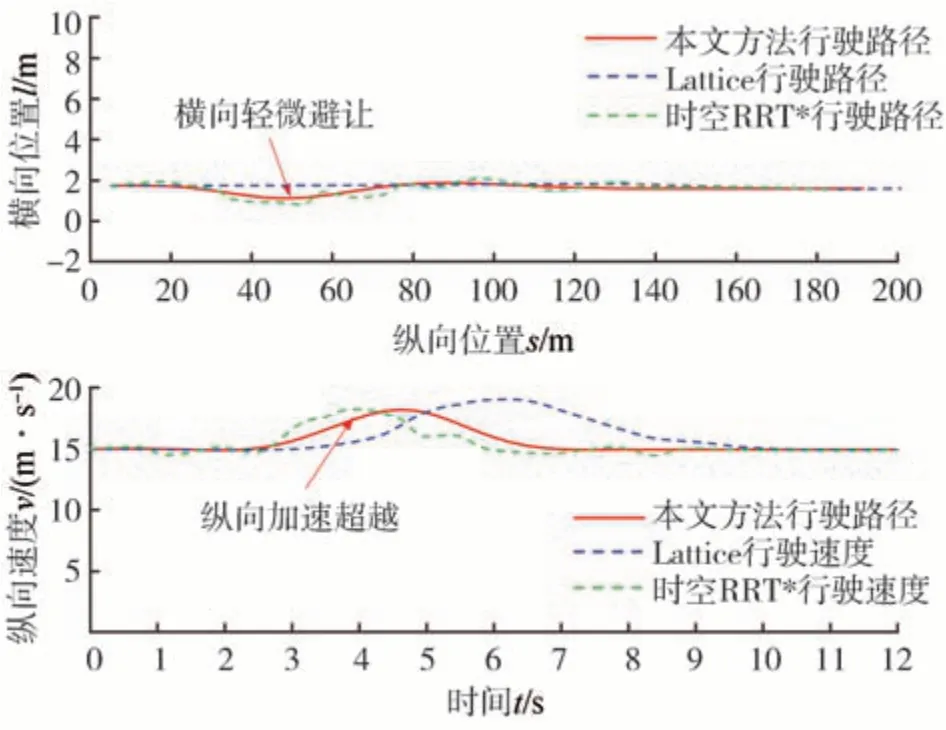
图18 旁车切入过程不同规划方法对比（场景一）

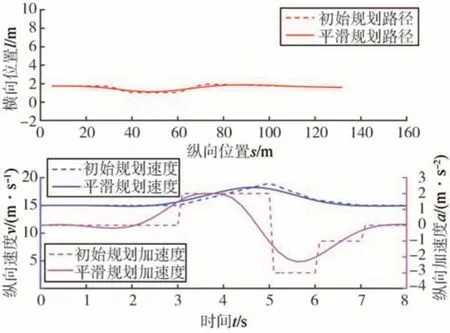
图19 旁车切入路径及速度、加速度规划结果（场景一）

图18 绿色曲线所示的时空RRT*行驶轨迹与本方法相近，但其同样存在路径和速度频繁抖动，且规划结果没有本文方法合理。图18 蓝色曲线所示的Lattice 方法选择纵向加速超越切入车辆V1，但与本文方法不同的是，其行驶路径在横向上无任何避让行为。这是由于解耦规划方法无法在路径规划中考虑具有时间属性的动态障碍物，只能由速度规划进行处理，因此以Lattice 为代表的解耦方法很难灵活应对这类需要进行横纵向联合处理的动态场景，行为表现过于机械，规划结果不够合理。

（2）旁车切入场景二

车辆V1 从初始位置（15 m，5.25 m）处以10 m/s的初始车速加速切入自车车道（切入完成后车速达到15 m/s）；车辆V2 从初始位置（75 m，5.25 m）处以10 m/s的初始车速做匀速直线运动。

仿真实验结果如图20 和图21 所示，由于旁车V1 切入车速较高，综合考虑碰撞风险和通行效率，t=1.57 s 时，自车选择减速避让切入车辆V1，同时在车辆V1 切入点附近向右进行轻微避让以降低碰撞风险。在t=4.21 s 时，车辆V1 切入过程完成，此时由于相邻车道仍被车辆V2占据，自车选择跟随前车V1 行驶。图21 中 Lattice 方法的结果与本文相似，自车选择纵向减速避让切入车辆V1，然后跟随前车V1行驶，但其行驶路径仍旧没有类似本文所提方法的横向轻微避让行为。

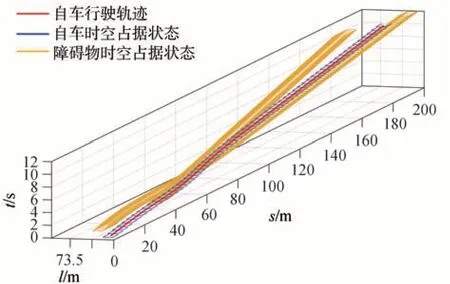
图20 旁车切入过程三维行驶轨迹（场景二）

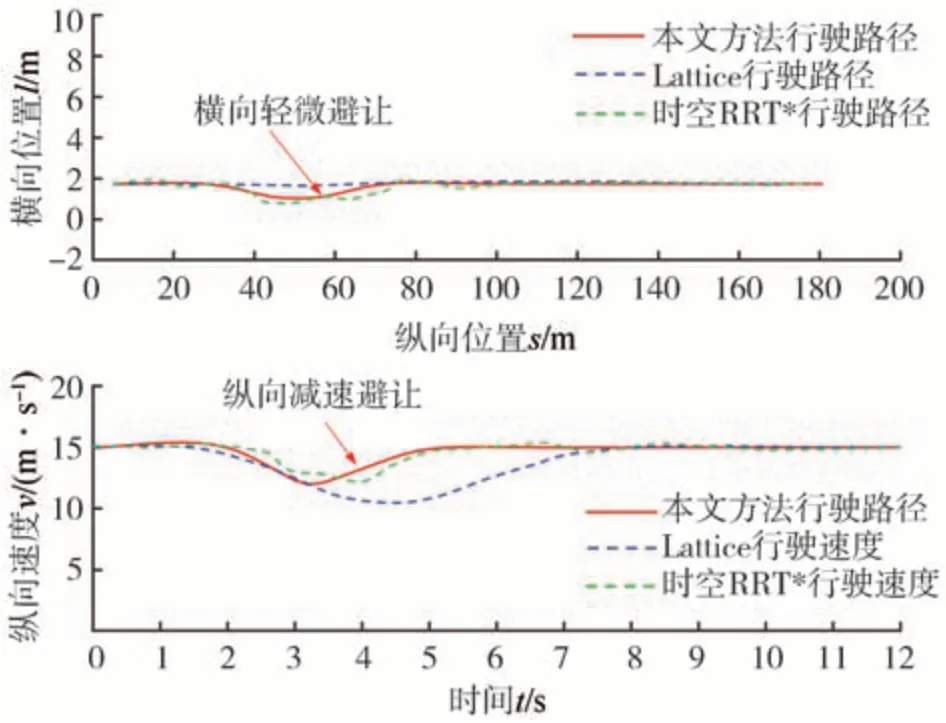
图21 旁车切入过程不同规划方法对比（场景二）

图19 和图22 分别展示了本方法在其中一个规划周期的轨迹规划结果对比，同样可以看出，经过上述时空轨迹后处理的平滑过程，可使规划出的最终路径、速度及加速度更加平滑，轨迹舒适性更好，且有利于控制模块进行轨迹跟踪。

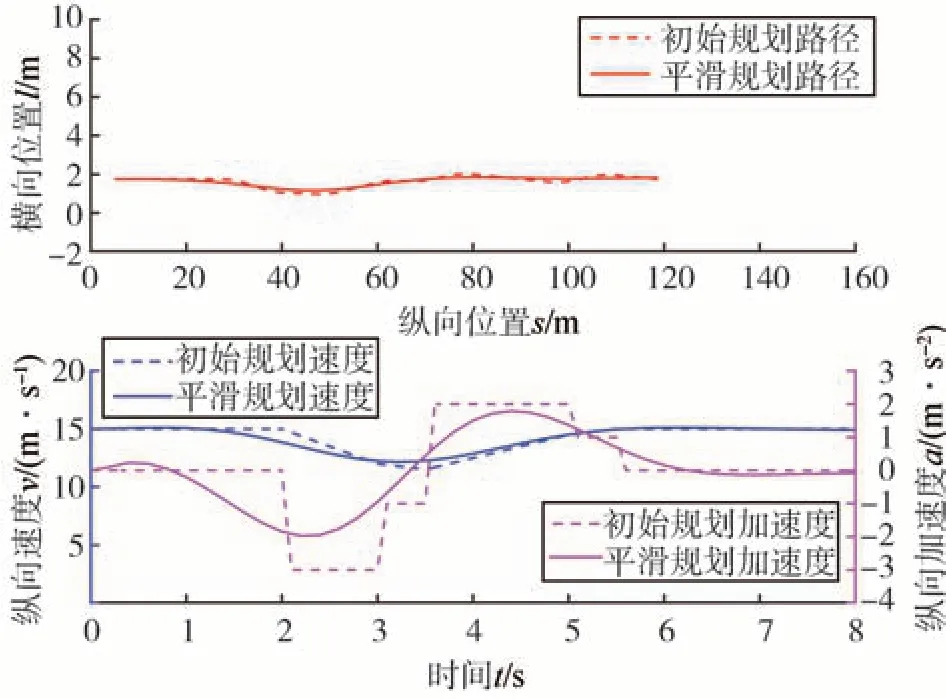
图22 旁车切入路径及速度、加速度规划结果（场景二）

3.3 算法实时性分析

仿真电脑配置为Intel i7-11800H/16GB RAM，MATLAB 版本为2020a。使用MATLAB 优化工具箱中的quadprog 求解器进行二次规划求解，并将MATLAB程序转成C代码执行以提升运行速度。

基于前述设计的换道超车和旁车切入两类典型场景，随机设置障碍物的初始位置及运动状态，每类场景重复实验100 次，统计本文所提方法及另外两种规划方法的平均耗时情况，结果如表3所示。

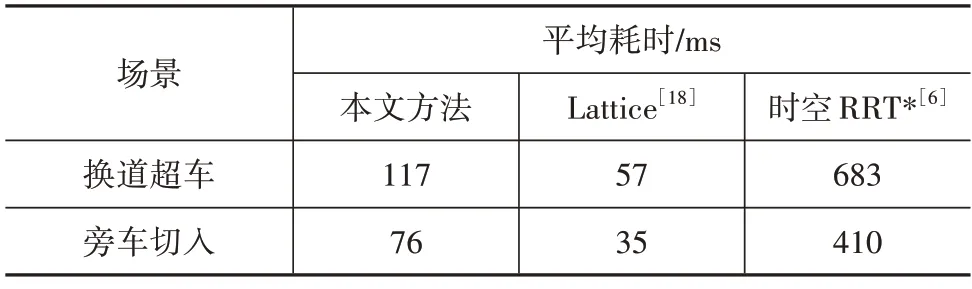
表3 算法实时性分析

本文所提方法的计算耗时相较于传统解耦规划方法Lattice 有所增加，但显著低于时空联合规划方法时空RRT*，同时本文方法的灵活性和规划结果合理性显著提升，因此较好地平衡了轨迹求解效率和求解质量。此外，值得说明的是，若将本文所提方法直接用C++进行实现，同时使用OSQP等求解效率更高的优化求解器，可进一步提升本文方法的计算实时性表现。

4 结论

本文提出了一种基于分层架构的智能汽车时空联合规划方法，在三维时空范围内统一处理静态和动态障碍物并进行轨迹直接求解，有效提升了轨迹规划质量。首先使用改进混合A*进行轨迹粗搜索获得初始轨迹，在保证轨迹搜索效率的同时，显著提升了轨迹规划的灵活性和结果的合理性。然后使用数值优化的方法对初始轨迹进行平滑后处理，通过引入安全可行驶时空走廊简化时空避碰约束，保证了轨迹优化过程的实时性。仿真结果表明，本文所提方法相较于传统时空解耦规划方法，灵活性更高、规划结果更加合理，同时具有较好的计算实时性。未来将对障碍物轨迹预测的不确定性进行建模，以适应实际复杂驾驶场景的需要。