面向变曲率道路的自动驾驶汽车换道博弈运动规划与协同控制研究*

林 程，汪博文，吕沛原，宫新乐，2，于 潇

（1.北京理工大学，电动车辆国家工程研究中心，北京 100081；2.清华大学车辆与运载学院，北京 100084）

前言

不合理的换道行为容易造成安全事故，道路曲率和环境车速的变化也会使风险成倍增加，严重影响道路交通安全及通行效率。随着车路云一体化融合系统的发展，打破了车辆间仅通过自身传感器获取周围环境及自身信息的局限性。通过网联化技术，建立自动驾驶多车系统协同运动规划方法，可以实现驾驶安全减少交通拥堵［1］。近年来，自动驾驶运动规划问题受到了广泛关注［2］。现有的换道合流研究中大多聚焦于车辆纵向控制，并依靠于简化的质点模型，其可以很好地应用于直道场景中，而在变曲率道路下仍有很大挑战。

在变曲率道路上进行多车协同运动规划须综合考虑合流时机和横向运动控制。目前针对选取合适合流时机问题，传统智能车辆中，基于场景驱动的决策控制方法被广泛采用。其主要是根据指定的判断条件，如安全距离和碰撞时间（time to collision，TTC）等，进行自适应巡航（adaptive cruise control，ACC）、换道避障（collision avoidance，OA ）和紧急制动（autonomous emerging braking，AEB）等驾驶模式的切换［3］。文献［4］中通过考虑不同道路、车辆横纵向状态来对周车环境风险进行评估和决策。另外，网联化技术的发展衍生了协同自适应巡航技术（cooperative adaptive cruise control，CACC），其通过综合考虑多车信息，可以更加安全地实现车辆跟驰和换道等动作［5］。然而，人类复杂的个性化驾驶行为难以简单地用既定规则进行描述，多车协同驾驶下的高收益的驾驶决策仍须被进一步探索。

随着硬件计算能力的逐渐提高，优化类的方法如模型预测控制（model predictive control，MPC）［6-7］，因其能够处理多约束多目标问题，被尝试用于求解高收益的协同驾驶多车决策。其核心思想是将协同运动规划问题转化为一个具有多约束的非线性优化问题［8］，通过求解可以得到最优决策控制策略。求解该问题的方法可以分为集中式和分布式两类架构。集中式的方法依赖于一个中心协调单元，能够得到系统最优的协同控制策略，但是往往须具备较高的算力［9］。例如，结合期望车道等离散变量，可以将多车换道模型转化为一个带约束的集中式混合逻辑动态（mix logical dynamic，MLD）系统［10］，通过混合整数规划来进行最优换道决策求解。分布式的方法不需要中心单元，只需自身及周围环境信息，在实际中更易于部署［11］。如文献［12］中，提出了一种随机MPC 换道决策与控制框架，通过获得其他车辆状态进行概率预测并得到换道最优运动控制。文献［13］中利用鲁棒MPC 实现了参数不确定下的无偏置多车运动控制。另外，与其他经典交互模型相比，采用基于博弈的换道模型能对人类多车交互行为进行更个性化的描述［14］。博弈论，如纳什均衡［15］和斯塔克伯格博弈［16］，通常采用分布式的架构来搭建车辆决策模型，两种非合作决策博弈方法的比较在文献［17］中列出。

机器学习方法如强化学习（reinforcement learning，RL）［18］、深度强化学习（deep reinforcement learning，DRL）等［19］在近几年发展迅速，其有在复杂环境中进行准确决策的潜力。文献［20］中提出了一种基于深度强化学习的多车协同决策框架，文献［21］中采用模仿学习和强化学习相结合的方式进行换道决策。由于模型的不可解释性和对数据的依赖，RL 算法较难在实际车辆中使用。为此，文献［22］中提出了一种优化嵌入式强化学习，以实现多车自适应决策。文献［23］中设计了一种混合强化学习算法，结合物理模型和历史数据得到最优策略。总的来说，机器学习方法能够很好地处理决策问题，尤其适用单车智能，但在多车协同的场景仍须进一步地研究。

另一方面，道路曲率变化下横向运动控制至关重要，车辆位姿和状态的描述是进行协同决策的基础。为了方便描述系统内多车之间的关系，虚拟队列方法，即将处于不同车道上的车辆近似看作成一个车道上的队列，常被用于冲突区域下的协同合流控制之中［24-25］。而在这些研究中，通常将变化的曲率道路投影视作直线，或默认忽略不计，且较少考虑非线性横向动力学的影响。为了消除曲率变化带来的影响，文献［26］中利用道路中心坐标来描述车辆的运动，并设计了一个面向超车避障的模型预测控制器，但是仅适用于单车决策控制。

不同于仅考虑单车或多车集中式协同控制的方法，本文综合考虑动态道路曲率变化和周车运动状态，提出一种基于博弈的多车分布式换道合流运动规划与协同控制方法。为了准确描述车辆位置姿态与道路之间的关系，本文首先分析了曲率坐标系下车辆横纵向运动对车间安全的影响机制，建立了多车交互动力学模型。之后，提出了适配变曲率道路的多车博弈速度规划算法，设计两步骤分布式地求解兼顾安全、效率、舒适多目标最优的速度轨迹及换道时机，缩小优化问题求解规模，提高计算求解效率。最后，通过变频率采样B 样条曲线识别道路曲率，构建基于前步最优控制反馈的自适应时变模型预测控制算法（adaptive time-varying MPC，ATVMPC）实现轨迹跟踪，通过每一步实时迭代更新控制矩阵和状态矩阵，减少了纵向车速和曲率变化带来的控制偏差累积。联合仿真结果表明，提出的方法能够更好地适应道路环境的变化，较传统方法能够选取高效益的合流时机并准确地跟踪目标轨迹。

1 曲率坐标系下多车系统模型

1.1 曲率坐标系

合理地描述车辆姿态与道路之间的相对位置关系对自动驾驶运动规划起着重要作用。传统笛卡尔坐标系往往是基于大地坐标，通常需要从大地坐标系转化为车体坐标系进行车辆状态计算。当车辆沿着曲率道路行驶时，大地坐标系下的坐标X和坐标Y具有极强的非线性关系，使车身姿态的描述更加复杂，因此采用曲率坐标系来描述车辆在全局道路下的位姿。图1 展示了不同坐标系之间的关系，其中曲率坐标系以给定的任意曲率参考线为基线，以沿着基线走过的距离作为纵向位移si，以垂直于该基线的误差作为横向偏移ey，i。定义车辆i在曲率坐标系下的位置坐标向量为

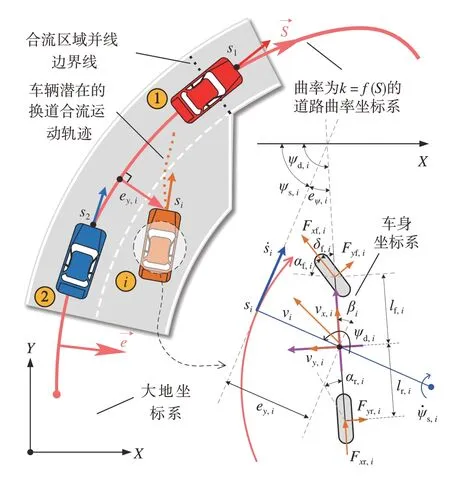
图1 不同坐标系之间的车辆状态关系

式中eψ，i表示为曲率坐标系下的横摆角。图1 中：vx，i和vy，i代表在车身坐标系下的车辆横向和纵向速度；ψd，i为大地坐标系下的车辆横摆角为对应的横摆角速度；ψs，i=ψd，i-eψ，i表示中心线切线与大地坐标系横轴的夹角表示相应的横摆角速度；δf，i表示车辆的前轮转向角；Fxf，i和Fxr，i为前后轮纵向力；Fyf，i和Fyr，i为前后轮的横向力；lf，i和lr，i分别代表质心到前轴和后轴的距离；βi为大地坐标系下的质心侧偏角；αf，i和αr，i表示车辆的前后轮胎侧偏角。

1.2 车辆动力学模型

变曲率道路下须综合考虑车辆的横纵向动力学性能。车辆的动力学特性表现为外界作用力对车辆的影响，分别定义车辆i的动力学状态向量xi和控制向量ui为

式中ai表示车辆坐标系下的纵向加速度。为了更好地考虑变曲率道路下的车辆动力学特性，以适应动态工况下的精确跟踪控制，保证多车协同驾驶的安全性和稳定性，采用如下横纵向动力学模型对状态进行描述，其中各个状态之间的几何关系可以在图1中得到。

式中：mi为汽车质量；Iz，i表示车体转动惯量。

由于变曲率道路下轮胎发生侧偏和滑移的概率较大，轮胎力表现出高度非线性横向动力学特征，一个高保真的非线性轮胎模型对车辆的精确控制至关重要。当侧偏角较大时，轮胎力的非线性特征明显，由于魔术轮胎公式能准确地拟合不同工况下的轮胎力学特性，被广泛应用于车辆在极端工况下的轮胎力描述。当侧偏角较小时，线性轮胎模型可以很好地描述轮胎横向力与侧偏角之间的线性关系，由于其计算简单通常应用于一般工况的车辆控制中。综合线性轮胎模型和魔术轮胎公式的优势，采用如下混合轮胎模型对前后轮胎侧向力进行建模：

当车速较低（＜6 m/s）且前轮转角变化率较小时，为了降低模型计算复杂度，同时也避免车辆动力学模型在车速为零时产生奇点的问题，采用简化的车辆动力学模型如下：

式中βi的计算表达式为

1.3 多车交互行为描述

为了更好地在曲率道路下描述车辆动力学特性及多车间的相对位置关系，本部分首先推导曲率坐标系下的纵向车速横向车速和横摆角速度的表达式。如图2 所示，先将有横向偏差的车辆投影至基线上，根据基线上的投影和实际所在位置之间的相对关系可得：

图2 曲率坐标下车间相对位置关系

式中k(si)表示曲率坐标下沿着纵向位移si的曲率变化函数，其具体计算方法将在第3 部分进行详细分析。图中(Xc，Yc)代表车身坐标系。带有上标“＇”的参数表示在基线上的投影。

其次，当在变曲率的道路环境中存在多辆车时，传统笛卡尔坐标系下常采用欧几里得范数的方法来描述车辆之间的安全关系，即

当虚拟队列间存在dr≤dsafe时，说明此时车辆i和j在基线上的投影存在重叠，此时换道会有潜在碰撞危险。

为了方便后续描述，综合姿态向量pi和动力学向量xi，将车辆i的状态统一表示为

2 多车博弈运动规划方法

2.1 多车拓扑通信构型

车间信息流拓扑模型对多车系统的协同控制有着重要影响。本文中，研究对象为多辆自动驾驶汽车，且假设车车通信的信道是理想的，不存在延时和丢包的情况，重点检验基于博弈的控制方法对多车系统综合性能的积极影响。合流区域采取的通信拓扑描述如图3 所示，每辆跟随车辆可以获取对应领导车辆的状态信息，并通过车路协同的设备对周围其他环境车辆信息进行信息补偿。

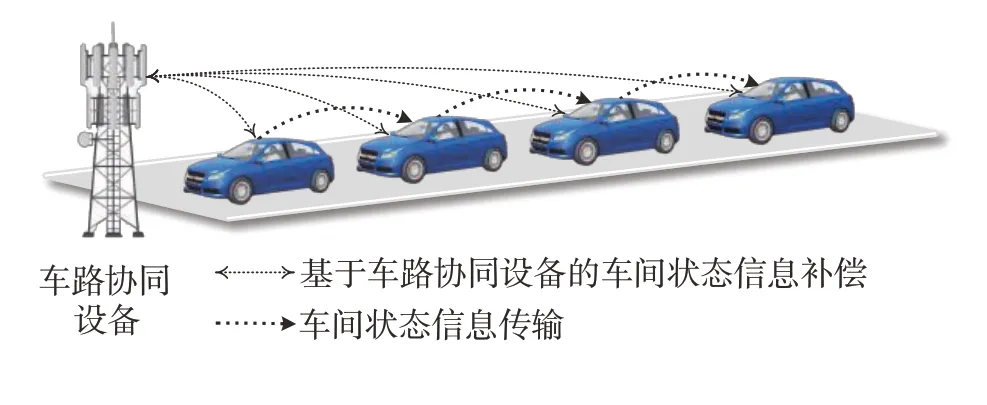
图3 通信拓扑示意

2.2 多车博弈系统描述

为保证合流过程中车辆行驶安全和系统整体道路的通行效率，多车协同换道合流的控制目标为规划出理想的纵向速度轨迹并选择合适的合流时机，并最终保持安全间距以及按照期望的车速行驶。当不存在外界扰动时，对于车辆i，j∈N，协同控制的目标可以表示为

基于上述控制目标，将变曲率道路下的多车协同速度规划问题转化为多车博弈问题，博弈的目标是总代价最小。一个博弈问题G主要由3 个部分组成：

式中：N 代表车辆集合；A 代表车辆动作集合；πi表示第i个参与者的策略集；J 代表车辆代价集合。本文在速度规划算法中综合考虑了自动驾驶汽车的个性化驾驶偏好及整体通行效率，通过驾驶安全性、乘坐舒适性和通行效率的比例来进行表征，同时也作为博弈收益组成的重要参考。

首先，驾驶安全性的代价由自车与环境车之间的碰撞时间倒数和安全相对距离两部分组成，并通过系数来调整各部分权重。其中，将碰撞时间倒数定义为

式中Δsij和Δvs，ij分别代表车辆i和车辆j在曲率坐标系下的相对距离和速度。基于式（14），将驾驶安全代价写作

式中kΔt和kΔs为碰撞时间因子和相对距离因子的权重系数；H(⋅)为阶跃函数，如式（16）所示。

式中κ∈R代表函数H(⋅)的自变量参数。

为保证系统内车辆能按照期望车速运行，快速到达合流点并完成合流动作，减少速度损失，本文定义效率代价：

乘坐舒适性通常与车辆加速度和加速度增量相关，定义乘坐舒适性系数为

式中Δai表示车辆的加速度增量。

结合式（14）～式（18）综合考虑车辆安全、舒适、效率，构建车辆i博弈总体代价函数Ji：

2.3 多车分布式博弈算法

多车博弈的目标是选择合适的时机进行合流并得到使所有交通参与者代价最小的速度曲线。对应的最优联合策略集合为A*，表示为

需要说明的是，将未来N步的多车预测状态也考虑在内，因此得到的结果是未来一段时间内的纳什均衡，最终得到的最优动作策略同样是带时间信息的状态序列：

为了得到车辆i的纳什均衡策略将预测最小博弈代价问题转化为N步预测域下的有限时域约束优化问题：

式中：zi=[si，vs，i]T；Ai和Bi为自车i状态矩阵和控制矩阵；l代表虚拟队列中车辆i的前方车辆。当在t时刻车辆i前方无车辆时定义sl，vs，l=+∞，同时将匝道合流点视作在车道处的静止障碍物为由简化的运动学模型推导得到的其他车辆的状态矩阵和控制矩阵；amin、Δamin和amax、Δamax分别为加速度控制量和控制增量的上下边界。

为进一步求解得到多车系统的纳什均衡策略集A*，本文构建了多车分布式换道博弈速度规划算法来对式（23）进行求解。如算法1 所示（表1），分两个主要步骤来得到最优速度控制策略和换道时机。首先，通过单步求解算法1中第4行的标准二次优化问题得到系统内每一辆车的最优速度控制策略然后，基于该策略和式（19）计算换道时刻在t～t+N-1时的综合代价集合：

式（24）集合中最小代价对应的时刻即作为车辆i的最优换道动机不同于集中式的优化方法，分布式的优化方法的核心在于采用多个节点来优化全局目标函数，算法中节点的含义对应系统内的每一辆车。通过节点间的相互信息交换，使得所有节点上的局部目标函数之和最终收敛于全局目标函数的最小值。因此基于算法1，最终可以得到系统纳什均衡的速度控制序列和换道时刻

3 多车横向运动控制方法

3.1 基于B-样条的曲率计算及路径规划

道路曲率的准确识别和预测是影响控制因素的关键之一，一般可通过采样计算来得到道路曲率，此外，也可通过拟合曲线进行近似计算。B 样条曲线是B-样条基数函数的线性组合，相比于贝塞尔曲线，B 样条曲线能指定阶数，并且在改变某个控制点情况下不会影响大范围的曲线变化。基于上述特征，合理设置B 样条曲线控制点个数能够准确地估计道路曲率，同时可预测未来曲率状态。然而由于道路曲率实时多变，且偶尔会伴随着突变的发生，增加了曲率识别的难度，为了能够在变曲率道路上快速地识别曲率并规划出参考轨迹，本文设计了基于B 样条曲线的自适应采样方法来计算和预测曲率，如图4所示。定义生成的k阶B样条曲线如下：

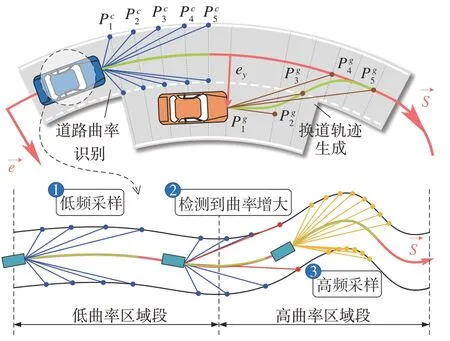
图4 曲率识别和路径规划示意

式中：P0～Pn表示为在车道保持和换道合流两个典型场景下的采样点，即可定义样条线曲线的走向和界限范围的控制点；λ是一组由非递减的连续变化值构成的节点矢量；Bi，k(λ)是第i个k阶B 样条基函数，其具有德布尔-考克斯递推式，见式（26）。

为了使拟合曲线尽可能地逼近真实值同时减少计算采样的频率，本文采用变频率控制点采样的方法生成B 样条参考曲线，即当车辆检测到当前路段的曲率变化较小时，进行低频采样；当预测到未来路段曲率将增大时，转化为高频率采样。由于B 样条曲线的局部支撑性和可微性，增加更改控制点可以仅改变局部的曲线，整体曲线不会受到很大影响。因此，自适应采样的方法可以保证实时识别曲线的光滑性和完整度，以及曲率的准确性和连续性。

基于上述讨论，定义通过B 样条曲线拟合的N步预测域下的横向参考轨迹为

3.2 自适应时变模型预测控制算法

道路曲率变化给车辆循迹控制增加了难度，尤其需要执行横向运动控制时，需要综合考虑轮胎的动力学因素、曲率和纵向车速的变化。在传统线性模型预测控制中，状态方程中的状态矩阵和控制矩阵均为常矩阵，即将车速或轮胎刚度设为定值。这种方法可以很好地应对一般工况，而当道路曲率变化导致车辆表现出非线性动力学特征时，预测模型则无法真实表达车辆状态，进而会造成较大的控制误差，甚至会引发算法失效。为此，本文设计了自适应时变预测控制算法对车辆进行协同控制。

首先，通过泰勒展开式线性化车辆模型：

基于式（28），定义时变状态矩阵Actrl，i和控制矩阵Bctrl，i为

式（29）可表示为标准状态方程形式：

进一步将式（30）离散化。下面以第k步的预测为例进行描述，离散化式（30）后可以预测第k+1步的车辆状态增量为

对于车辆名义状态量和控制量的预测更新，通过前向欧拉公式可以得到离散方程。对于车辆i在时刻t下第k+1步的名义状态量和控制量可表示为

基于式（31）和式（32），预测估计车辆i在时刻t下的第k+1步状态ξi和输入ui：

进一步地，将跟踪问题转化为一个N步预测域的标准凸约束优化问题：

上述过程只能保证在单步计算过程中得到最优控制。为了能够降低曲率、车速等参数的连续不断变化造成的控制误差，本文中提出了如图5 所示的自适应时变模型预测控制算法（ATV-MPC）。其特点在于，基于上一步预测得到的最优控制，在每一时刻t下迭代更新状态矩阵和控制矩阵从而减少曲率、车速频繁变化带来的控制偏差累积。在当前时刻计算结束后，将中第一个元素作为输入作用于被控车辆之中。

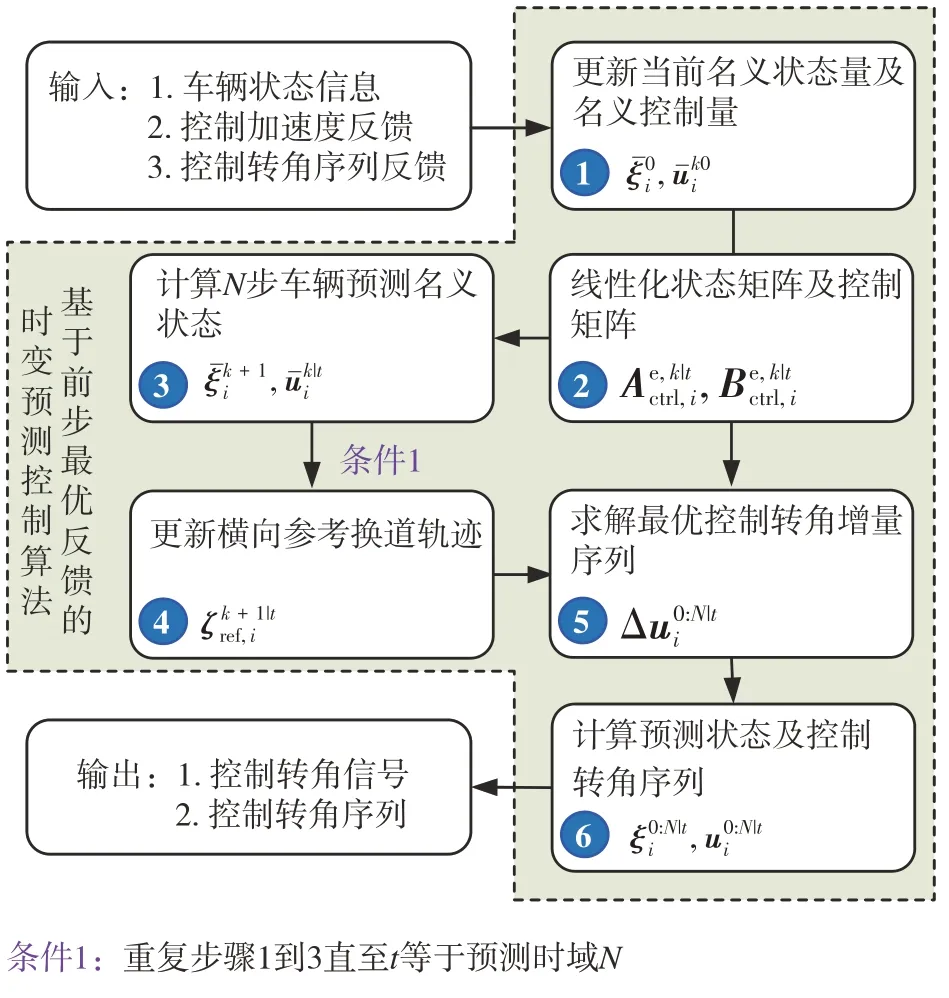
图5 自适应时变预测算法流程

4 仿真结果与分析

4.1 仿真平台及框架

为了验证所提出的面向变曲率道路的多车协同控制算法的有效性，本文基于MATLAB 和CarSim 的联合仿真平台进行算法实现和场景搭建，整体算法的框架流程如图6 所示。本文构建了一个单向双车道的变曲率道路场景，并选用4 辆自动驾驶汽车作为实验对象。此外，设计了车道保持和换道合流两种工况进行验证。

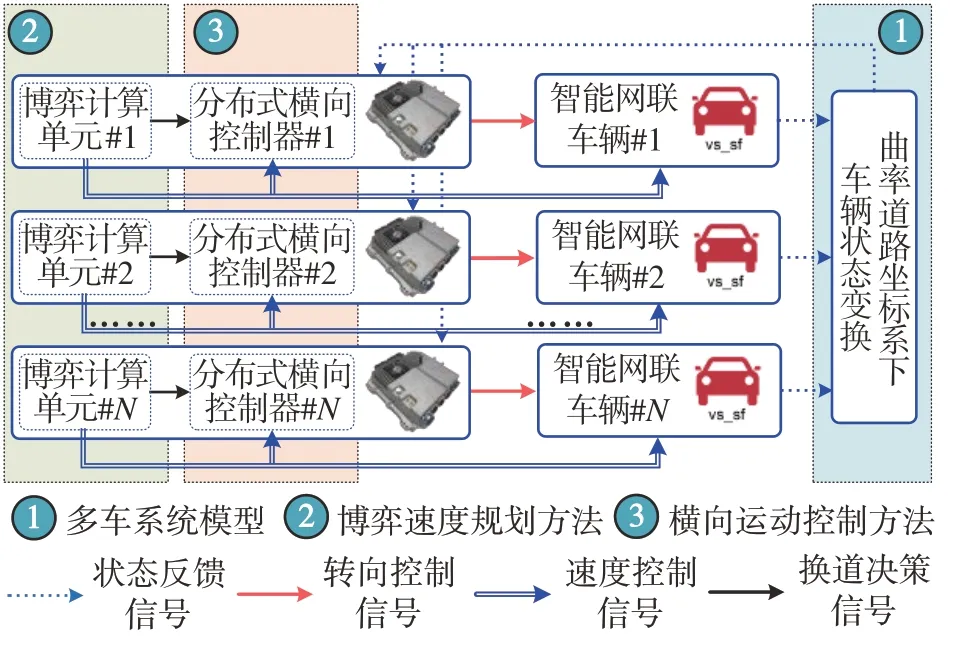
图6 整体算法框架

预测控制中的时域大小对计算效率和控制效果有很大影响，时域过短会削弱预测控制的精度；过长的时域则会导致预测模型误差增大，计算效率下降，难以达到理想的控制效果。因此，凸优化问题的预测时长通常选择在0.6～1 s 左右［27-28］。本文选择预测时长为1 s，其中预测域N=10，步长ts=0.1 s。其他参数如表2所示。

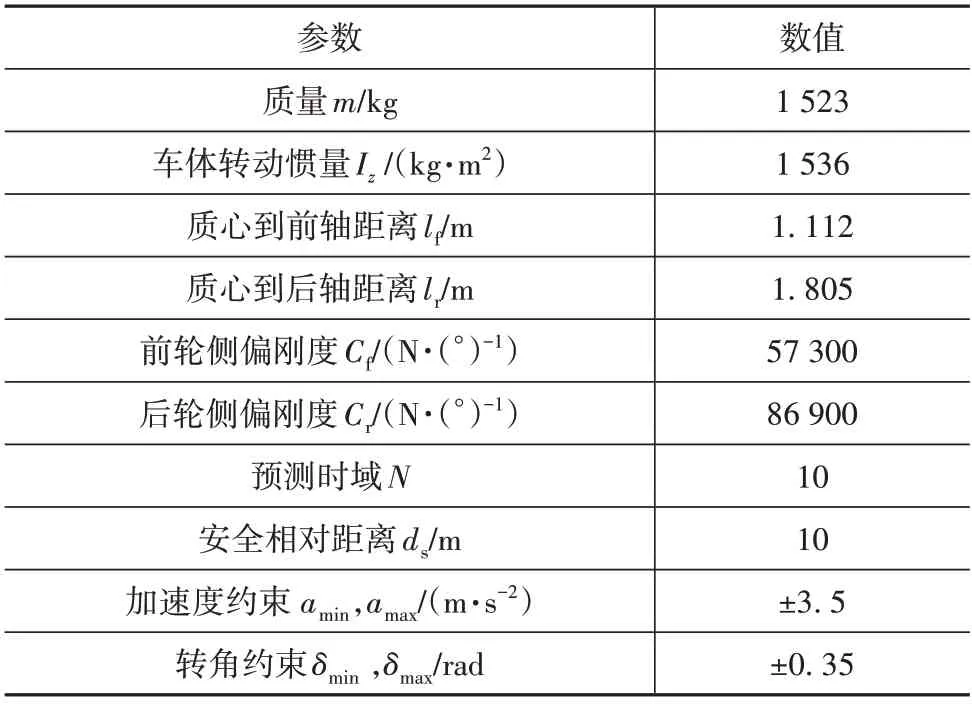
表2 仿真参数设置

4.2 车道保持性能仿真

为了评估横向运动控制算法的性能，在设置的车道保持场景中，4 辆智能网联车均设置在同一车道上行驶，并采用经典的斯坦利（Stanley）算法和未采用变频率采样B 样条曲率计算的时变预测控制算法进行对比。

图7 展示了协同控制算法对测试道路的曲率识别结果。对比算法为未采用变频率采样B 样条曲线曲率计算方法，可以看出当曲率发生较大变化时，容易产生剧烈波动，曲率是计算控制量的重要参数，数据的频繁变化会严重影响控制精度。相比较，提出的算法能够根据B 样条曲线显示地预测未来曲率变化从而优化采样频率，消除了数据的震荡，减少了对后续控制的影响，相关结论也可在图8中看出。

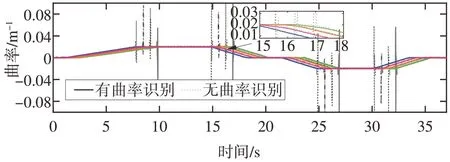
图7 曲率识别计算结果

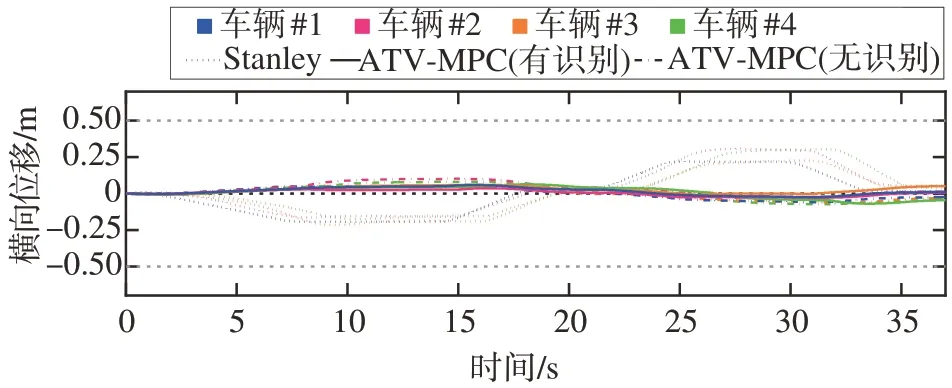
图8 横向跟踪结果

图8 为本文提出的横向跟踪控制算法在变曲率道路上的仿真结果，图9 为仿真过程中的转角变化。随着道路曲率的增大，3 种算法的跟踪误差都会有所增加。经典Stanley 算法由于未系统地考虑车辆横向动力学，控制误差较大。相比较而言，文中提出的基于最优状态反馈的时变预测控制算法能够减少58%的跟踪误差。同时可知，更加精确和平滑的连续曲率能够降低控制过程中转角的频繁波动，是减少控制误差的关键。

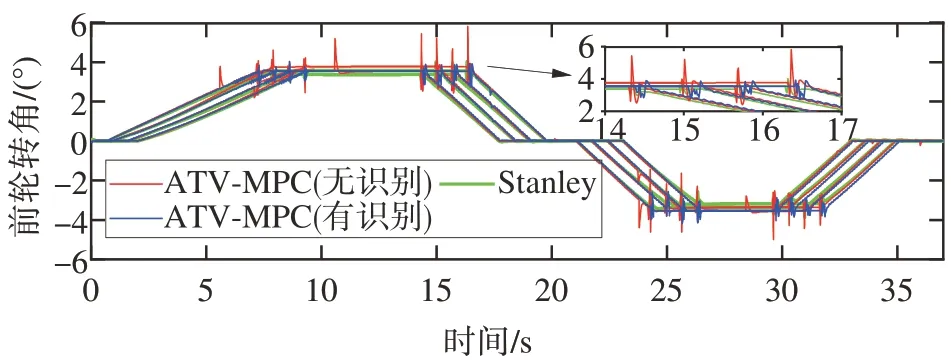
图9 前轮输入转向角

4.3 换道合流性能仿真

本部分搭建的实验场景用于检验变曲率道路下协同控制算法的换道合流性能。道路曲率变化与场景1 设置相同。图10 为CarSim 中的仿真时刻截图，在距离起点50 m 处增加了道路合流点，车辆#1和#3被设置在右车道，车辆#2 和#4 在左车道。为了便于观察，图11 展示了各车在曲率坐标下的相对位置。控制目标是使道路中所有车辆高效安全地通过设定的合流点。测试中选用集中式MPC 算法和协同自适应巡航算法（CACC）进行比较。

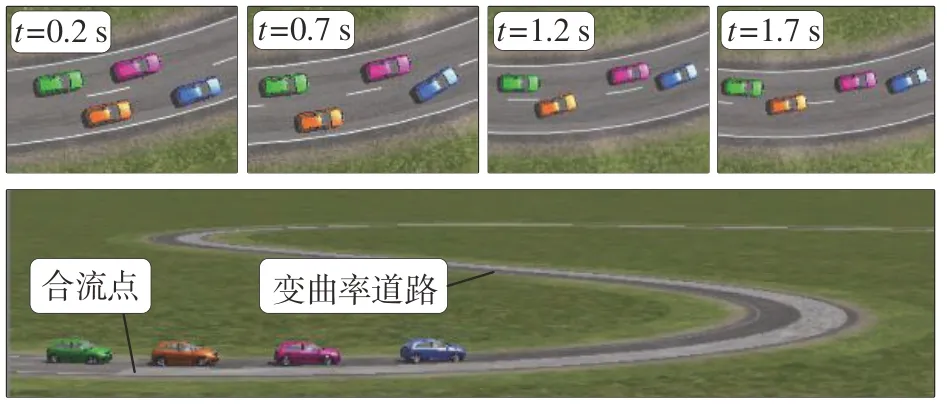
图10 CarSim仿真时刻场景图

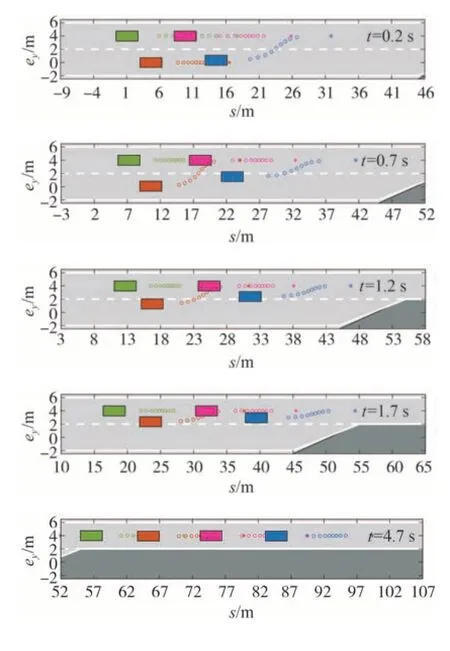
图11 曲率坐标系下投影的时刻场景图

图12～图15 展示了在该场景下3 种协同控制算法下的车辆状态变化。图12 给出了车辆相对距离的变化大小，从投影时刻图11 和图12 中可以看出，车辆#4 起始的质心处相对距离均在4～5 m 左右，在本文提出的速度规划方法的作用下，相对距离逐渐增大，并最终能够稳定安全地达到理想的相对距离。相比较而言，集中式MPC 的方法也能够更快地实现类似的效果。CACC 算法尽管也能最终实现期望值，但是在控制过程中会造成较大波动。

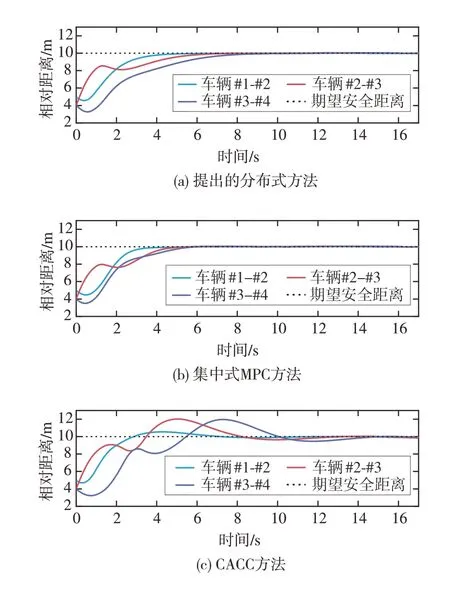
图12 相对距离变化结果

图13显示在3种算法下的碰撞时间倒数均维持在-0.2～0.2 范围内，由文献［29］中可知均处于安全状态。而提出方法下各车碰撞时间倒数值略低于另外两种方法，且数据分布更加集中，能够实现更加安全稳定的多车协同驾驶。

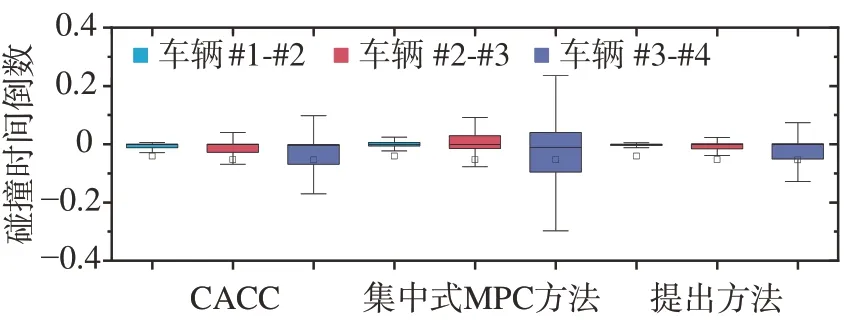
图13 碰撞时间倒数结果

类似的结论也可以从图14 车速变化和图15 加速度变化中得到。车辆#1 处于最靠近合流点的位置，故3 种算法下车辆#1 和车辆#3 先加速，车辆#2和车辆#4 减速来创造更多安全换道的空间。之后，在速度调节算法的作用下，均趋向于理想车速。由图可知，无论是集中式还是分布式，本文中提出基于博弈的速度规划方法能够使各车车速平稳地变化到期望车速。而在CACC 方法下各车速度和加速度变化超调量大，波动频繁，镇定时间长。

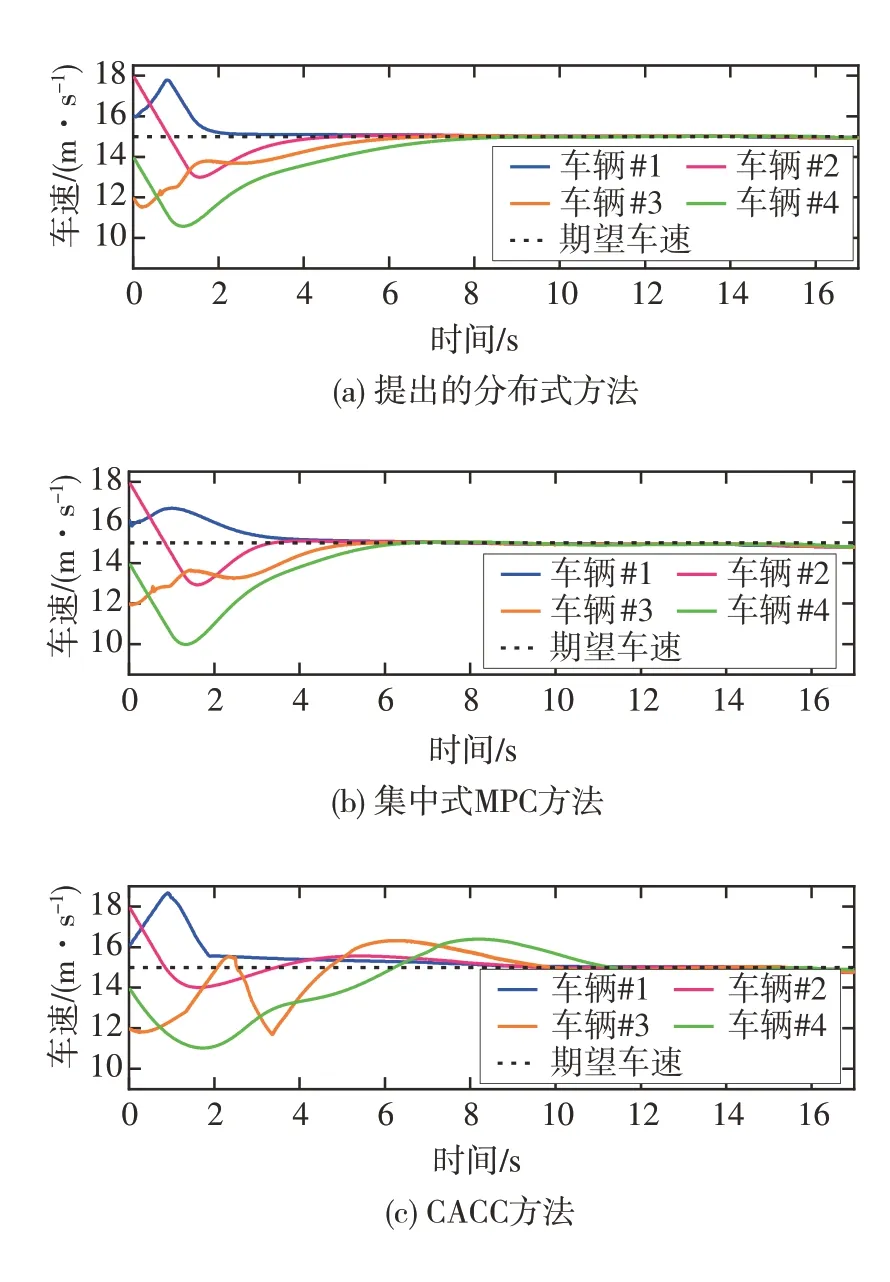
图14 车速变化结果

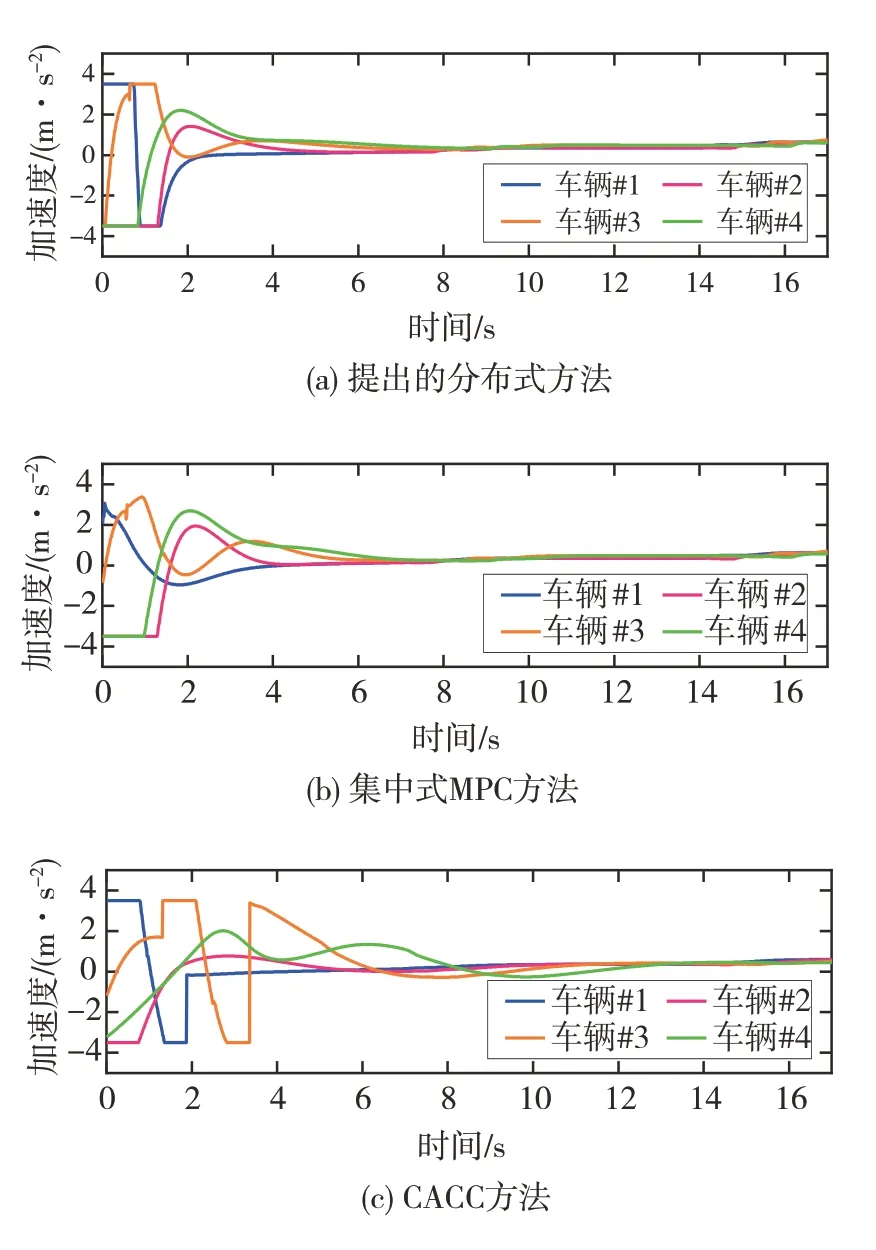
图15 加速度变化结果

图16 展示了车辆的横向位移变化。从图中可以看出，在本文提出的横向运动控制算法的作用下，车辆均能够准确跟踪期望横向轨迹。此外，在不同算法作用下车辆#1 和车辆#3 的换道时机均不同。基于博弈的方法能够判断出更具有效益的换道时机。相比较而言，CACC 方法下的车辆换道时刻更加保守。

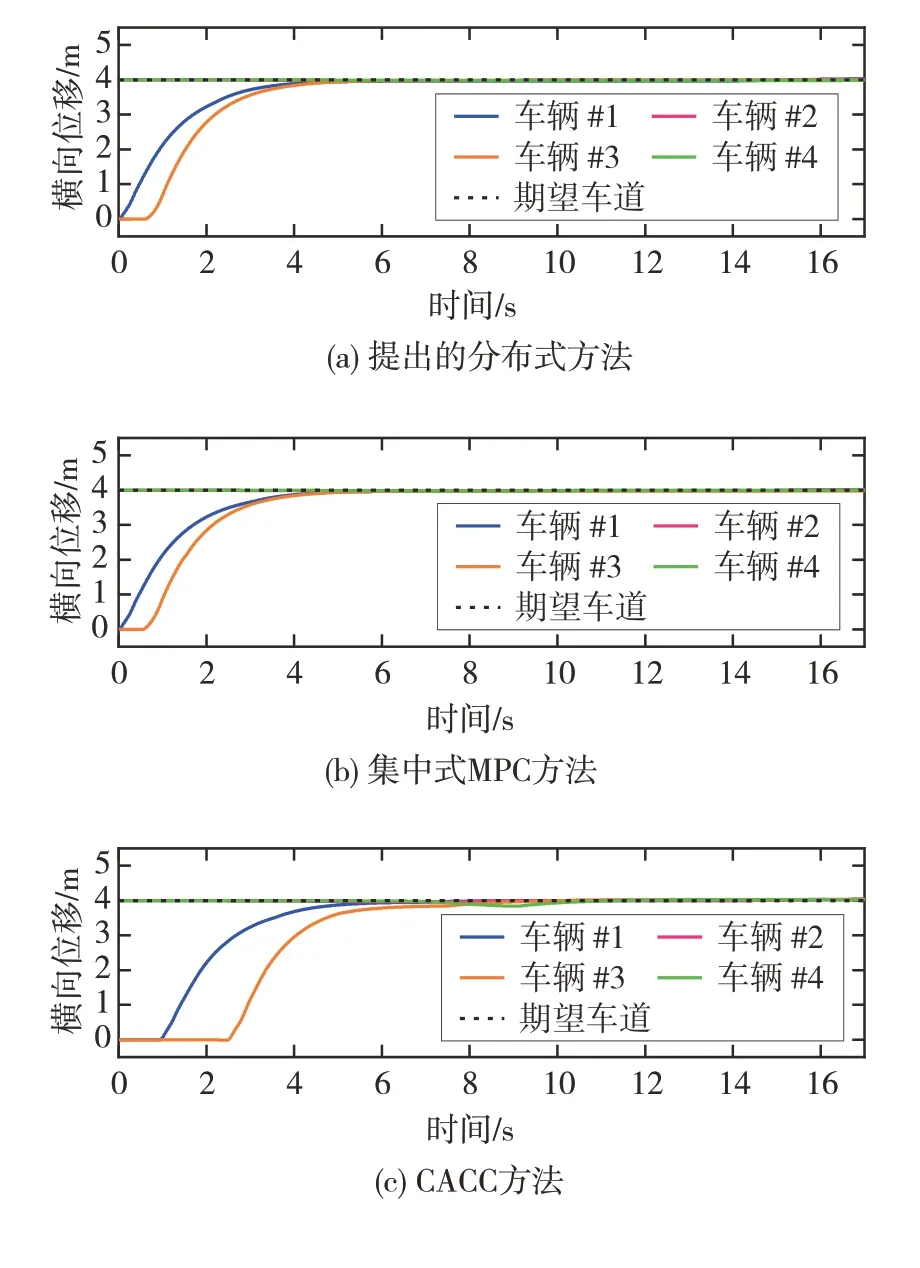
图16 横向位移变化结果

为了更加直观的展示换道时机的选取，图17 和图18 给出了有换道需求的车辆#1 和车辆#3 的代价变化，其中当换道代价突变至20 左右时表明此时车辆已通过合流点。对于车辆#1，如图17 所示，博弈的算法判断在起始时刻综合的代价最小，最终车辆#1 在当前时刻即实施了换道动作，直至到接近1.7 s完成换道，此时的换道博弈代价要远高于原始车道代价，车辆即继续保持在已换道结束的车道上行驶。CACC 算法下的车辆#1 在初始时刻换道代价显示具有高收益，但是车辆仍然等待到2 s左右后才执行换道行为，合流效率降低。与车辆#1 不同，车辆#3 需要合理地并入到车流内部中，如图18 所示，在初始时刻换道博弈的代价要高于原始车道代价，直至0.5 s左右算法判断此时换道具有高收益，车辆#3选择执行换道合流。

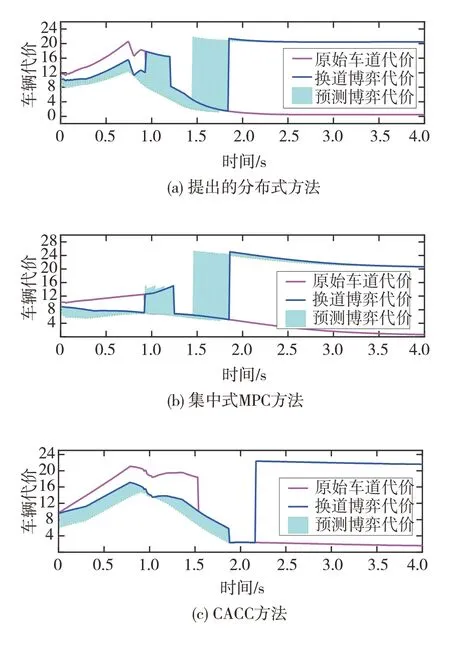
图17 车辆#1换道与原始代价

图18 车辆#3换道与原始代价

图19归纳了3种算法下的换道时机和对应的广义换道代价。结果显示，相较于CACC 算法，提出的基于博弈的方法无论集中式还是分布式都能以更低的代价获取更高效益的换道时机，节省了74%的合流时间，提高了协同换道合流的效率。

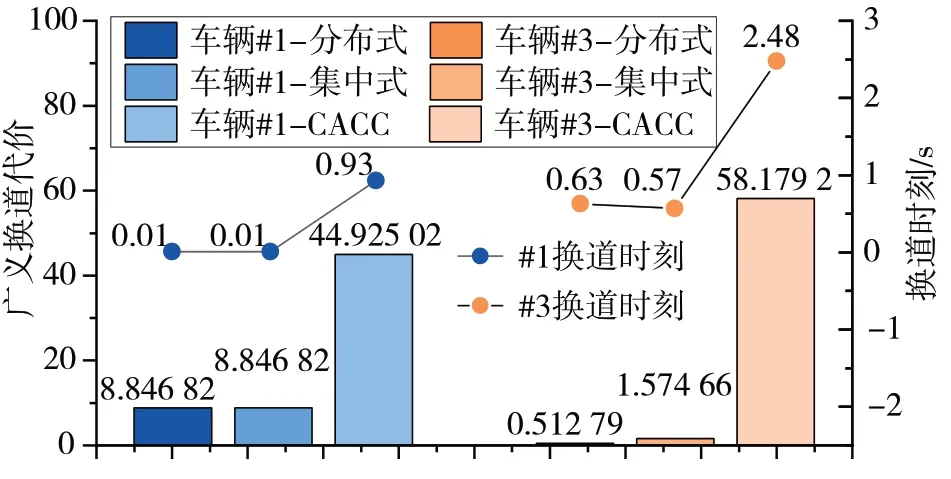
图19 广义换道代价结果

图20 给出了算法分别在集中式和分布式两种架构下的计算效率，表3 归纳了两种架构下的优化问题规模。结果显示，分布式算法计算效率更高，计算时间仅为集中式MPC 的10%，从而降低了算法对硬件设备的需求，更容易在实际中部署。

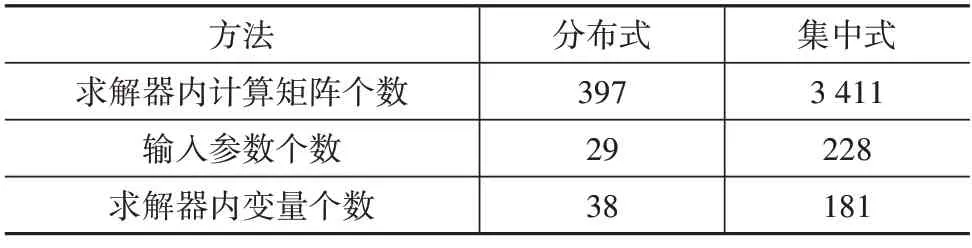
表3 优化问题规模

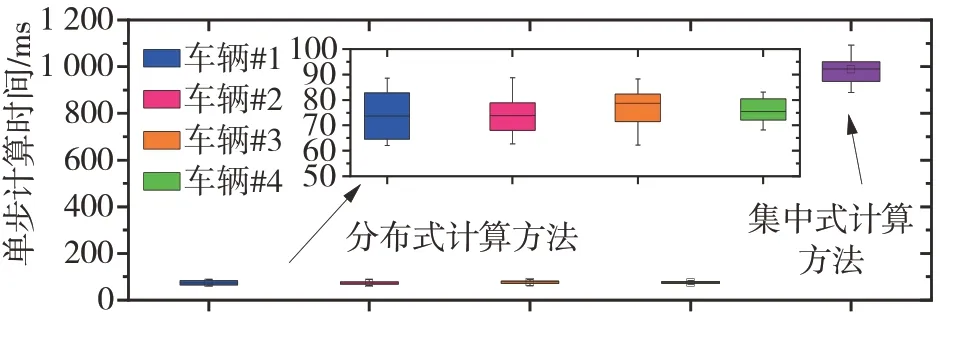
图20 单步计算时间结果

5 结论

为使多自动驾驶汽车能够安全高效地在高动态的道路环境中执行换道任务，本文中提出了一种基于博弈的多车换道合流运动规划与协同控制方法。主要研究内容如下：（1）分析了曲率变坐标系下的车辆运动状态，解析了车辆之间的相互影响机制，建立了多车交互动力学模型。（2）通过系统地考虑道路环境信息，提出了基于博弈的多车协同速度规划算法，并采用分布式框架计算多车最优速度轨迹及换道时机。（3）基于变频率采样的B 样条曲线识别的道路曲率及规划的路径，构建了自适应时变预测控制算法实现底层轨迹跟踪，在车速和曲率频繁变化时仍能保证控制策略的有效性。

分别在车道保持和换道合流两种测试场景下对算法进行验证，结果显示提出的协同控制方法能够选取最高效的换道时机，同时保证驾驶安全和控制精度。其中，相比于经典横向运动控制Stanley 法，提出的方法能够改善时变工况下的轨迹跟踪性能，减少58%的跟踪误差；相比于CACC 法，提出方法能够规划更平滑安全的速度轨迹和具备更高效益的换道时机，减少74%的合流时间；相比于集中式MPC的方法，提出方法能缩小优化问题规模，计算求解效率仅为集中式MPC的10%。

在后续的工作中，将考虑混合交通流中存在的各种不确定因素，并结合学习类的方法，使本文提出的协同控制方法能够应用于具有更加复杂多变的道路场景中。