汽车行驶轨迹数据密度峰值聚类算法研究*

江浩斌，路保松，李傲雪

（江苏大学汽车与交通工程学院，镇江 212013）

前言

随着定位设备的广泛使用，人们采集了大量移动体的轨迹数据，诸如船只货运、道路车辆、动物迁徙、人类行为、飓风等。轨迹数据是包含时间戳的一组位置点集成的时间和空间信息，蕴含了丰富的运动模式和重要的现实意义。

聚类分析是一种用于数据挖掘的技术，是一种无监督的机器学习方法，可以在没有先验知识的情况下，按照一定规则划分类簇，使得同一类簇样本相似度高的同时不同类簇样本的相似度低。目前针对轨迹数据的聚类研究已经得到了广泛关注，例如，利用船舶自动识别系统记录的数据对船舶轨迹进行聚类分析，用于海上交通研究［1］；对出租车行驶轨迹进行聚类分析，用于研究城市交通热点，规划城市路线［2-3］；使用聚类算法预测用户移动行为并进行兴趣点推荐［4］等。

密度峰值聚类（density peaks clustering，DPC）是一种特殊的密度聚类算法，该算法最早被Rodriguez等［5］发表在《Science》期刊上。该算法通过计算样本的局部密度和相对距离确定类簇中心，进而将其余非中心样本按相似度分配给最近的类簇。与密度聚类和均值漂移法相同，DPC 可以聚出任意形状的类簇，并且不需要提前指定簇的数量。

DPC 算法简单有效，但在处理轨迹数据时存在以下问题：（1）没有统一的相似性度量准则［6］，不能准确定义轨迹间的相似度；（2）DPC处理高维数据集的效果不佳，而轨迹数据中隐藏着很多无关的噪声数据影响着距离度量的准确性；（3）计算局部密度时引入参数截断距离dc，该值的选择对聚类结果影响较大。

对于轨迹相似性度量的问题，许多学者提出了自己的见解。其中，欧式距离［7］是常见的一对一相似性度量，但是仅限于长度相等的轨迹。动态时间规整（dynamic time warping，DTW）［8］则可以量化不同长度轨迹之间的相似性，算法灵活且效果较好，但是结果受噪声点的影响非常大。最长公共子序列（longest common subsequence，LCS）［9］是基于编辑距离计算轨迹相似度，LCS 对噪声有一定的鲁棒性。Yoo 等［10］在DTW 的基础上，将DTW 中的距离项替换为Jensen-Shannon 散度和Wasserstein 距离的线性组合，重新定义了轨迹距离度量。Amir 等［11］提出了一种基于分段轨迹方向变化的轨迹相似性度量法。该方法利用光谱聚类对轨迹进行分割，提取子轨迹的方向变化后，采用特征向量测量轨迹间的相似性。

由于维度灾难的影响，聚类算法在面对高维数据时难以获得理想的聚类效果。主成分分析［12］是一种使用广泛的数据降维算法，其通过数学变换的方式将原始高维数据空间投影到能够突出数据主要特征的低维子空间上，有效缓解了维度灾难。Wang［13］将PCA（principal component analysis）应用到DPC 聚类算法中，经过实验证明了算法的可行性和有效性。Cao 等［14］将PCA 算法用于船舶数据集上，验证了算法在船舶轨迹聚类研究中的优越性。

DPC 算法在计算局部密度中定义的距离阈值dc需要人为选定，不确定性较高。针对局部密度计算中存在的问题，纪霞等［15］利用相对距离将数据映射到相对邻域中，再从相对邻域中计算数据局部密度，缩小了密度统计的范围。Ren 等［16］提出一种改进的基于分层k 近邻（k-nearest neighbor，KNN）的DPC 算法，该算法对数据进行分层并赋予不同权重，重新设计了局部密度的计算方法，在数据集上证明了算法的优越性。

针对DPC 算法在轨迹数据上的不足，本文就轨迹数据特性改进了DTW 相似性度量，在此基础上提出了一种k 近邻和主成分融合的密度峰值聚类算法（DPC-KP），该算法通过PCA 对轨迹数据进行降维，引入k 近邻思想计算局部密度，改进DTW 算法重新定义了样本间的相似性度量；同时，提出了一种适合于汽车行驶轨迹数据集的密度峰值聚类算法。

1 DPC算法

1.1 DPC算法原理

密度峰值聚类是一种特殊的密度聚类算法，该算法基于两个假设：（1）聚类中心被局部密度较低的邻居包围；（2）聚类中心与局部密度较高的样本间的距离相对较远。为了量化上述假设，引入变量局部密度ρi和相对距离δi，定义如下。

定义1 局部密度ρi：

式中：dij是样本i与样本j之间的距离；dc代表截断距离。对于大规模样本使用截断核即式（1）计算局部密度；小规模样本则使用高斯核即式（2）计算局部密度。

定义2 相对距离δi：

相对距离δi表示样本xi到局部密度比自身大且离自身最近的样本间的距离。

聚类中心应具备两个特征：局部密度ρi较高，相对距离δi较大。所以，通过绘制ρi-δi决策图可以确定其他簇中心。然后，将其余样本按相似度度量分配到局部密度比自身大且离自身距离最近的簇中心中，从而形成最终的聚类结果。算法步骤如下。

算法1 DPC算法

输入：样本数据L，参数dc

输出：聚类结果C

步骤1：计算各样本之间的相似度距离；

步骤2：依据式（1）计算样本的局部密度ρi；

步骤3：依据式（3）计算样本的相对距离δi；

步骤4：绘制决策图ρi-δi，找到密度峰值标记为类簇中心；

步骤5：将其余样本分配给局部密度比自身大且离它距离最近样本所在的类簇中；

步骤6：输出聚类结果C。

1.2 DPC算法不足

虽然DPC 算法在大多数情况下具有较好的效果，但仍存在一些如下不足。

（1）局部密度的计算。截断距离dc直接影响局部密度结果，而dc值又需要提前设定。不同的dc值在面对同一样本时，聚类结果可能大有不同。如图1所示，当dc值取的较小时，样本被分为3个类簇；当把dc值调大时，DPC 会将右方和下方类簇聚到一起形成两个类簇。

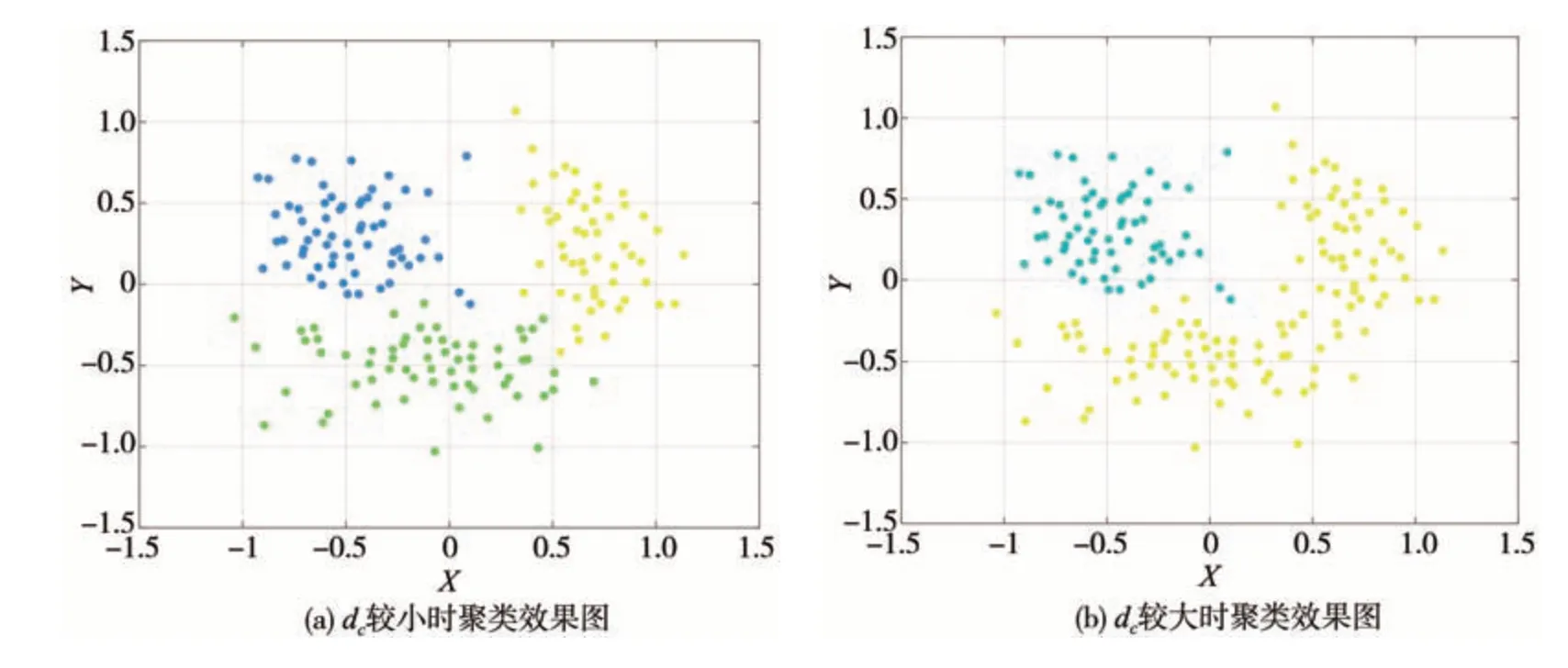
图1 截断距离dc对聚类结果的影响

除了dc值之外，局部密度度量准则对聚类效果也有影响。如图2 所示，当dc值相同时，同一数据集采用不同的高斯核函数会出现不同的聚类结果。

图2 局部密度度量对聚类结果的影响

（2）DPC 在按相似度分配非聚类中心时会产生连带错误。当某一样本在分配时发生错误，有可能会连带其周围的样本也分配到错误的类簇。这种分配错误不仅与DPC 分配策略有关，也和局部密度和样本相似性度量有关［17］。

2 DPC-KP算法

2.1 相似性度量

轨迹段之间的相似度描述相比于传统两点之间距离的描述更加复杂。线段具有长度和方向信息，不能简单地用欧氏距离来判断线段之间的相似性。Wang等［18］评估了LCS、DTW 等主流相似度测量算法在不同时间序列数据集上的准确性。实验结果证明，DTW 算法可以获得最为精确的相似度测量结果。本节我们改进原有的DTW 相似度算法，在保留其原有优点的基础上，改善其在轨迹形状分析方面的不足。

定义3 点-点距离

假设存在轨迹Li={p1，p2，…pi，…，pm}，pi-1(xi-1，yi-1)，pi(xi，yi)，pi+1(xi+1，yi+1)是轨迹Li中连续的样本点，点pmid1、pmid2分别是轨迹段pi-1pi和pi pi+1的中点，见图3。已知pmid1(xmid1，ymid1) 与pmid2(xmid2，ymid2)坐标为

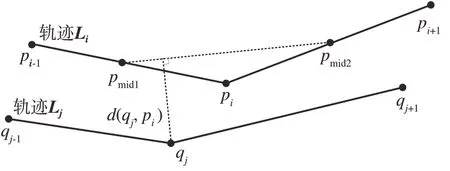
图3 点-点距离

同样，在图3 中给定另一条轨迹Lj={q1，q2，…，qj，…，qn}，其中3 个连续轨迹点分别为qj-1，qj，qj+1。

定义轨迹点qj(xj，yj)到pi两端轨迹段中点连线的距离d(qj，pi)为单向点-点距离。当轨迹点qj在线段pmid1pmid2上的投影点在该线段的延长线上时，单向点-点距离定义为轨迹点qj和与其相近的线段端点间的距离。因此，d(qj，pi)计算式为

同理，可以算出点pi到点qj两端轨迹段中点连线的距离d(pi，qj)。为了改善不同轨迹在对应路段轨迹点间隔不一致导致度量不准确的问题，将两个单向点-点距离相加得到的函数定义为轨迹点pi与轨迹点qj之间的距离D(pi，qj)：

定义4 段-段距离

分别给定轨迹Li和轨迹Lj的子轨迹段pi pi+1和qjqj+1。给出两子轨迹段之间的距离函数：

段-段距离示意图如图4所示，点q＇j和点q＇j+1分别是线段Lj两个端点在线段Li上的投影点。可以看出，两条轨迹段之间的夹角和它们的长度也影响着轨迹段之间的相似度。轨迹段间的夹角θ范围为［0°，90°］，当夹角越大时，两条轨迹的相似度越低。轨迹段pi pi+1和qjqj+1长度相差越大，两条轨迹的相似度也越低。然而，这些形状参数对轨迹相似度的影响并没有在模型中体现出来。

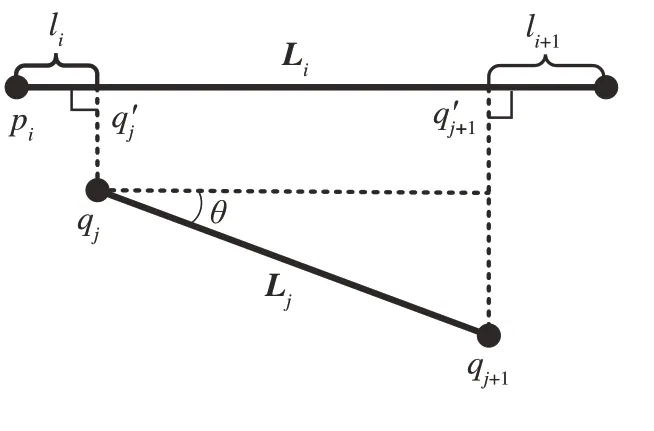
图4 段-段距离

通过上述对影响因素的分析，改进后的段-段距离为

式中：|li|+|lj|/max{Li，Lj}是调整轨迹段长度在距离函数中权重的调节因子；sinθ是轨迹夹角在距离函数中权重的调节因子。

在段-段距离的定义下，根据DTW 的思想计算累积距离作为两条轨迹间的距离：

式中：Head(L)表示该轨迹上的第一段轨迹；Rest(L)表示除去首段轨迹后的轨迹。

根据上述计算，累积段-段距离代表整条轨迹间的距离，从而量化轨迹间的相似度。至此，本文提出了适合汽车行驶轨迹数据的相似性度量模型。

2.2 主成分分析（PCA）

主成分分析是一种用于提高无监督学习效率的维度约减算法。PCA 的主要思想是将原始样本数据映射到更低维的子空间上，降低样本维度，凸显样本数据主要特征变化。假设存在样本X是一个M×N的矩阵，则降维原理如下。

调整每个样本属性具有相同的均值且为0。然后计算协方差矩阵∑：

计算协方差矩阵∑的特征向量，并将这些特征向量组成矩阵U：

式中：u1是最大的特征值对应的特征向量；u2对应第二大特征值，以此类推。

通过计算可以得到样本在(u1，u2，...，uM)上的表达：

式中下标“rot”表示一种从原始样本的旋转映射关系。若将其降至d维，则需保留Xrot的前d位非零成分，即

2.3 k近邻（KNN）

DPC基于截断距离dc和全局的样本分布求局部密度。算法主要考虑样本截断距离内的样本数量，致使密集区样本的局部密度大于稀释区样本，极大的影响了簇中心的准确性。针对该问题，本文引入k 近邻相对密度的思想，重新定义局部密度的计算方式。

假设轨迹样本Li、Lj，样本之间的距离表示为DTW(Li，Lj)，则Li的k个最近邻KNN(Li)表示为

通过KNN(Li)定义局部密度ρi为

该算法中存在唯一参数k，k定义为样本总数N与百分比p的积，即k=p×N。

样本点到其k个近邻样本的距离越小，则局部密度值越大。局部密度计算范围从原来的整个数据集缩减为样本的k个近邻样本，这样得到的局部密度仅与k近邻相关，能够更好地反映样本点的局部信息。DPC-KP 算法依据式（15）计算局部密度，依据式（3）计算相对距离，并绘制聚类中心决策图。

2.4 算法步骤

算法2 DPC-KP算法

输入：样本数据L，百分比参数p

输出：聚类结果C

步骤1：归一化样本，使其具有相同的均值0 及方差；

步骤2：依据式（10）计算协方差矩阵∑；

步骤3：计算协方差矩阵∑的特征值和特征向量；

步骤4：利用PCA算法对原始数据进行降维；

步骤5：按照式（9）计算样本间的相似性度量；

步骤6：按照式（15）计算样本的局部密度ρi；

步骤7：按照式（3）计算样本的相对距离δi；

步骤8：绘制决策图ρi-δi，找到密度峰值标记为类簇中心；

步骤9：将其余样本分配给局部密度比自身大且离它距离最近样本所在的类簇中；

步骤10：得到聚类结果C。

3 实验分析

为了验证DPC-KP算法的有效性，本节分别在人工合成数据集和真实轨迹数据集上进行实验。在二维样本点数据集上采用欧氏距离计算样本间的距离度量，在证明算法有效后使用2.1 节提出的轨迹相似性度量对真实轨迹数据进行聚类。参数p的选取范围为［0.1%，0.5%，1%，2%，5%，6%］。本节通过合成数据实验证明算法的可行性。通过真实轨迹数据集实验，证明DPC-KP 算法在轨迹数据上的有效性。

3.1 人工合成数据集实验

为了验证本文所提出的算法的有效性，实验选取12 个数据集其几何形状如图5 所示。图5（a）-图5（e）展示的D1、D2、D3、D4 和D5 数据集中包含的簇都有不同程度的重叠。图5（f）表示R15 数据集由分布不均的15 个簇组成，图5（g）是由样本点组成的交互曲线Spiral。图5（h）-图5（l）分别表示circles、jain、cth3、d6 和ls6 数据集。这些数据集均包含线型数据簇，更符合车辆行驶轨迹的形状特征。

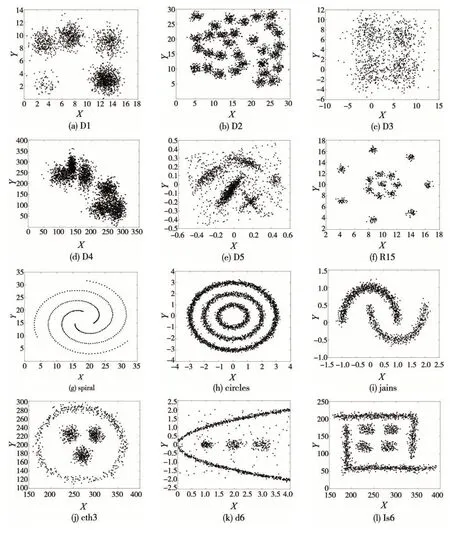
图5 人工合成数据集可视化

D型5个数据集在空间分布上具有变化复杂性。数据集分别有2 000、3 100、1 000、3 783、2 000 个样本点，各数据集样本点的重叠程度不同，如图6 所示。DPC-KP 聚类算法对于有不同簇个数、不同形状、不同重叠复杂性的数据集是有效的。

Spiral 是由312 个样本点组成的螺旋数据集。R15 数据集包含了600 个样本点，由15 个簇组成。DPC-KP 在该数据集上对于参数p的选择有很强的鲁棒性。图7 是这两个数据集分别在DPC-KP算法下的聚类表现。作为对比，图8 是在同样数据集下DPC 算法的聚类结果。通过效果图可以看出，所提出的算法通过改善局部密度的计算有效地解决了当样本簇间密度差别较大时产生的分配错误。

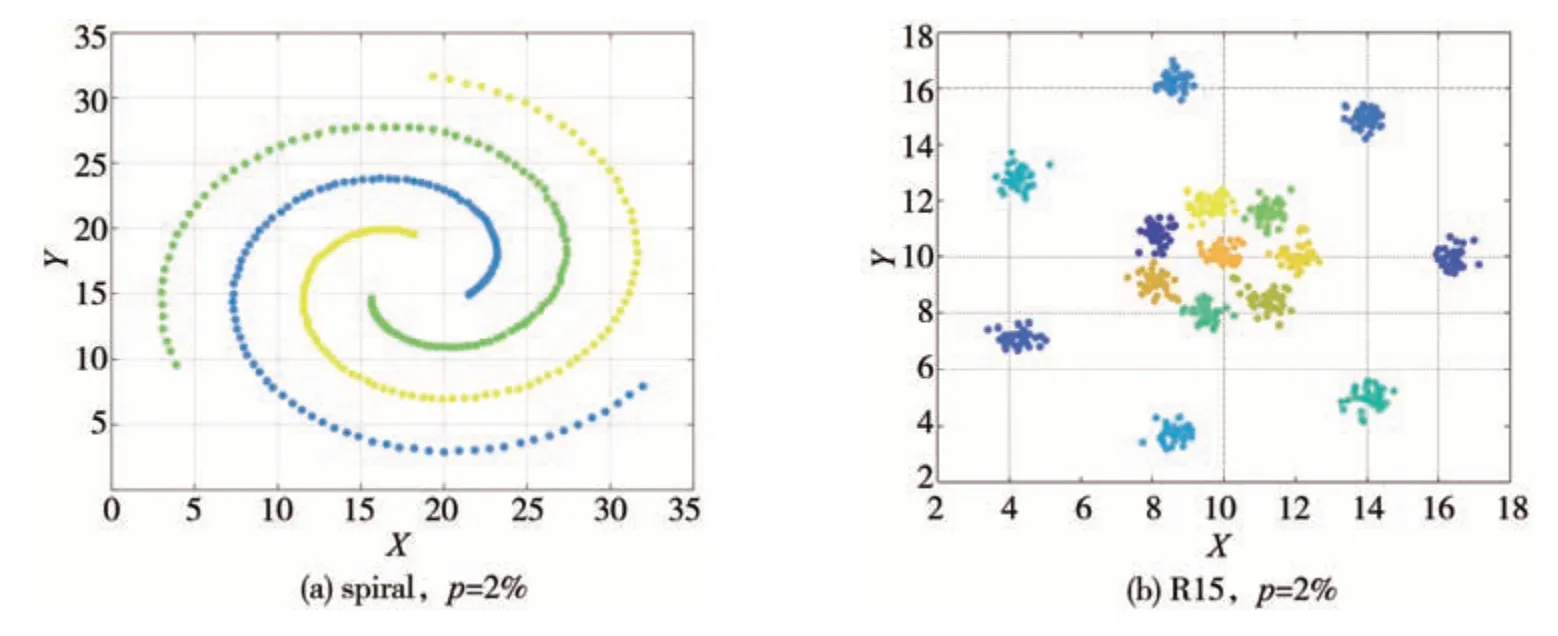
图7 DPC-KP算法在spiral和R15数据集上的效果图

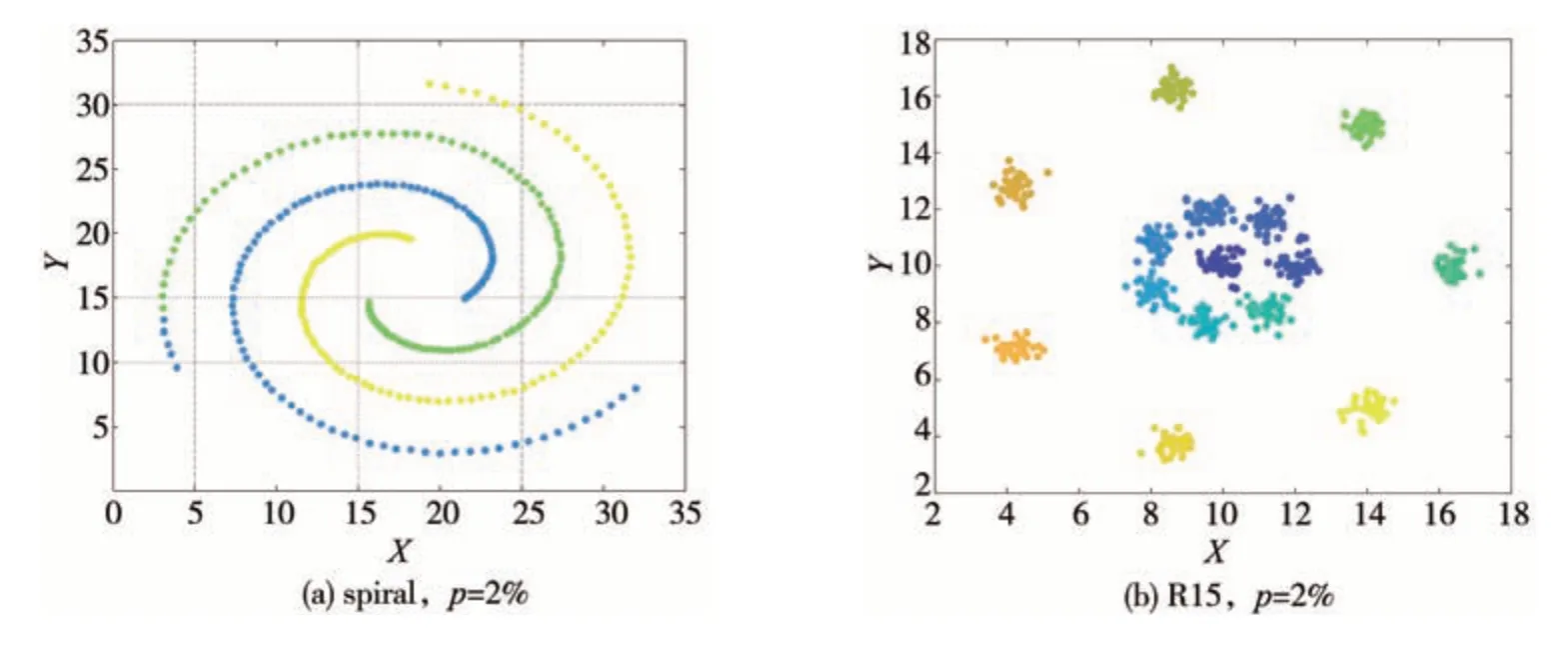
图8 DPC算法在spiral和R15数据集上的效果图

为了验证算法在车辆行驶轨迹数据上的有效性，测试了含有线型样本簇的数据集。Circles 由3 个嵌套的椭圆组成，共含有3 603 个样本点。Jains数据集有两个“C”字型簇，由1 502 个样本点组成。Cth3、d6 以及ls6 数据集分别含有1 146、1 400 和1 735个样本点，整体形状均为线型簇中包含若干点簇。DPC-KP 算法在这些线型数据集上的聚类效果如图9所示。从图中看出，DPC-KP算法能够识别出数据集中线型的簇并正确地完成聚类。

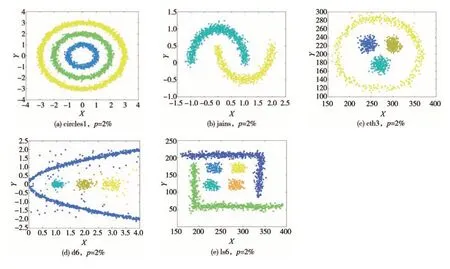
图9 DPC-KP在circles、jains、cth3、d6和ls6数据集上的聚类表现

为了展现聚类的效果，本文选取经典聚类算法k-Means 以 及DPC 进行精度值（cluster accuracy，ACC）比较。ACC 属于外部评价，需要知道数据的真实聚类结果C＇。ACC计算公式如下：

式中：i和i＇分别指聚类结果C和C＇中的簇类；k和k＇则是簇类数。ACC值通过计算C和C＇的匹配度量化聚类效果的好坏，该值越大，说明聚类效果越好。算法的比较结果如表1所示。

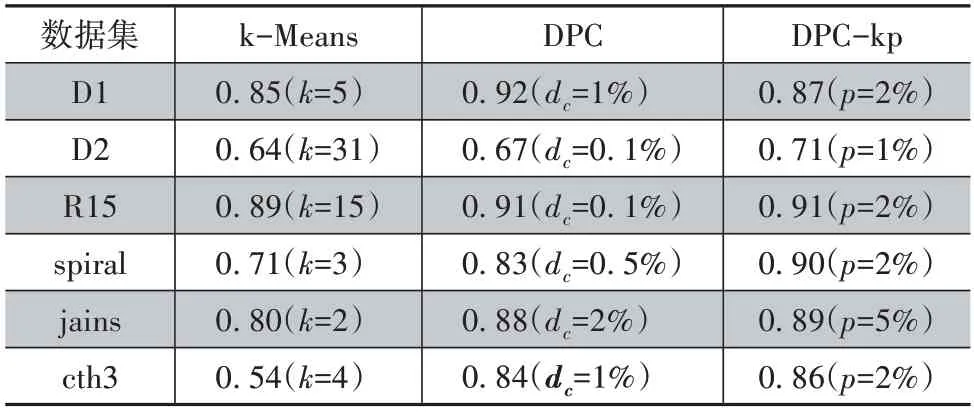
表1 不同聚类算法在数据集上的ACC值

可以看出在聚类常见的重叠数据集D1、D2、R15 时DPC-KP 算法效果与DPC 效果相近，均稍优于k-Means 算法。而在面对含有线形数据簇的数据集时，DPC-KP算法的聚类效果更好。

在上述人工合成数据集上的实验表明，所提出的DPC-KP 算法相较于DPC 算法在不同形状、不同重叠程度的数据集上有更好的聚类效果。并且，该算法能够很好地找到数据集中的线型簇，证明了该算法在轨迹聚类上的可行性。

3.2 轨迹聚类实验

为了验证DPC-KP 聚类算法在轨迹数据集上的效果，采用CVRR 轨迹数据集进行聚类实验。选取其中真实的直行高速公路汽车轨迹数据集I5_SIM和十字路口数据集CROSS 进行聚类，聚类效果如图10所示。

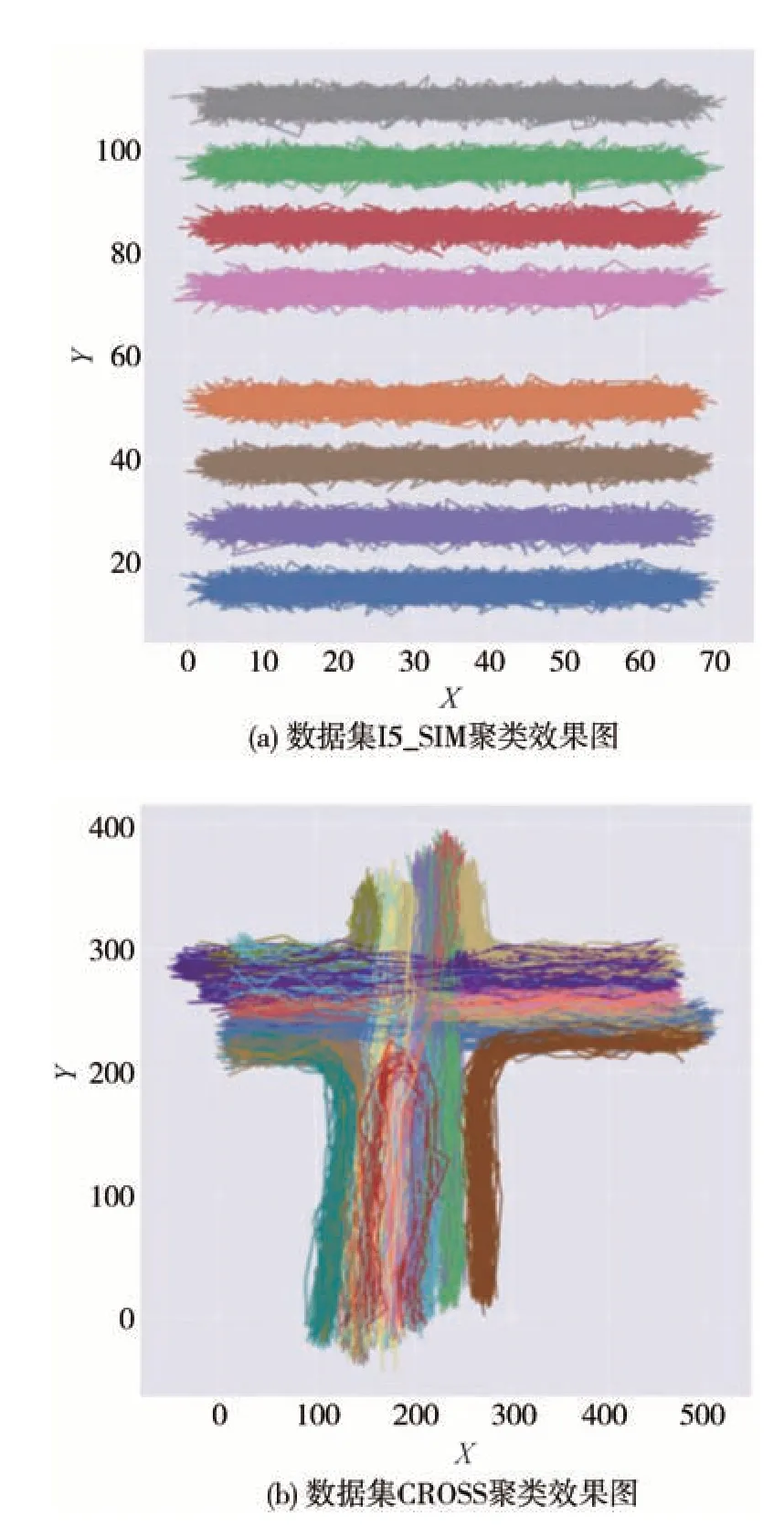
图10 DPC-KP在轨迹数据集上的聚类效果

I5_SIM 数据集展现的是双向交通的4 车道公路汽车轨迹（共8条车道），包含800条轨迹数据。可以看出，本文提出的算法可以准确地将轨迹数据按车道分成8 个簇。CROSS 数据集展现的是十字路口的汽车行驶轨迹信息，包含1 900条轨迹数据。算法将直行、转向及掉头轨迹都准确地完成了聚类。利用轨迹簇中样本的疏密，可以判断某时间段轨迹流的特征，用于指导交通设计和智能汽车仿人驾驶研究。

为了使实验更加真实可靠，使用激光雷达采集了环岛行驶汽车的轨迹数据进行实验。数据集预处理后聚类效果如图11所示。

图11 环岛数据集聚类效果图

图11 表明聚类得到的簇间差异大，聚类效果较好。同时，注意到该环岛南北向的车流量大于东西向车流量，这与采集时路况相符。但是，图11 中仍存在不合理的噪声轨迹数据，需要进一步识别处理。

4 总结

本文提出了一种适合于汽车行驶轨迹数据的聚类算法DPC-KP，该算法引入k近邻信息度量样本密度，避免了DPC 算法度量局部密度的缺陷，改善了样本分配时产生的连带错误。在轨迹数据特征维度高的情况下引入主成分分析，在预处理阶段对轨迹数据进行降维处理，方便找到轨迹数据中的主要特征变化。同时，注意到大数据下的轨迹聚类只能呈现轨迹簇整体的性状特征，只能从整体的角度分析交通流的相关特征。如要进一步根据轨迹特征分析驾驶行为特征，寻找汽车驾驶共性，则需要进一步找到代表性轨迹，全面考虑轨迹中体现出的驾驶信息。