基于轮胎分段仿射辨识模型的车辆行驶状态估计策略研究*

2023-07-31孙晓强王玉麟胡伟伟蔡英凤PakKinWong

汽车工程 2023年7期

孙晓强，王玉麟，胡伟伟，蔡英凤，陈龙，Pak Kin Wong

（1.江苏大学汽车工程研究院，镇江 212013；2.澳门大学机电工程系，澳门 999078）

前言

随着电控技术的快速发展，诸如自适应巡航控制、直接横摆力矩控制和防抱死制动控制等汽车先进电子控制系统在车辆上得到大规模应用［1-4］，使得车辆行驶稳定性和安全性得到极大提升。在车辆电控系统中，车载传感器的准确信号输入是实现高精度运动控制的关键前提。然而，一些车辆行驶状态往往难于通过传感器直接测得，或由于相关传感器的价格过于高昂，无法实现规模化搭载。因此，基于模型的车辆行驶状态估计成为行业研究热点［5］。

轮胎是车辆与地面接触的唯一部件，构建准确的轮胎力学特性模型一直是行业研究人员的关注焦点之一［6］。现有轮胎力学模型按构建方式主要可分为经验模型和物理模型两大类，包括“魔术公式”模型、幂指数统一轮胎模型、HSRI 轮胎模型和Dugoff轮胎模型等均属于上述范畴［7］。这些轮胎模型在相应的应用场合下均表现出优异的力学性能，对于推动轮胎力学模型的发展发挥了重要作用。然而，从车辆行驶状态估计角度来看，现有轮胎模型的构建方式仍存在一定的提升空间。由于在车辆行驶状态估计过程中需要反复调用轮胎模型，因此希望所调用的轮胎模型能够兼顾模型精度和计算效率。然而，现有轮胎模型大多形式复杂、参数拟合困难，主要侧重轮胎力学特性的拟合精度，并未考虑后续在此基础上进行车辆行驶状态估计策略的设计是否便利。因此，如何突破新型轮胎力学模型构建方式，有效协调轮胎模型精度要求与便于系统状态估计策略设计二者间的相互矛盾，具有重要研究意义。随着计算技术的快速发展和试验条件的不断完善，从系统输入输出数据出发，借助于数据挖掘、模型辨识等技术手段，有望解决本研究面临的轮胎非线性力学特性建模问题［8］。

近年来，许多先进的估计算法被运用到车辆行驶状态估计领域中，取得了丰富的研究成果［9-11］。Chen 等［12］建立了不确定奇异车辆模型，该模型考虑了轮胎侧偏刚度的时变特性，包括车辆动力学模型和轮胎模型的不确定性，在此基础上，设计了质心侧偏角鲁棒观测器，实现了良好的估计效果。Wang等［13］提出了一种鲁棒无迹卡尔曼滤波估计算法以提高传感器测量异常时的估计鲁棒性，噪声的影响由移动多项式卡尔曼滤波进行处理。容积卡尔曼滤波算法（cubature Kalman filter，CKF）作为一种高性能非线性滤波方法近年来得到广泛应用［14］，在此基础上提出的平方根容积卡尔曼滤波（square root cubature Kalman filter，SCKF）算法也引起广泛关注，相关算法主要通过保证对称性和正定性来提高估计精度。然而当目标运动状态突变导致模型失配或测量偏差导致异常值时，滤波精度便会降低。为此，本文中考虑在SCKF 框架下，结合强跟踪算法将得到的预测误差协方差乘以渐消因子。该因子能够让残差序列相互正交，从而能够尽可能多地从观测中提取有用信息，避免由于目标状态突变而导致的估计精度下降情况发生。

结合上述内容，本文在建立车辆2 自由度动力学模型的基础上，首先采用多输入多输出分段仿射（piecewise affine，PWA）辨识方法进行轮胎非线性侧偏力学特性的模型构建，进而实现整车横向动力学分段仿射建模。在此基础上，进一步运用强跟踪平方根容积卡尔曼滤波算法对车辆横摆角速度和质心侧偏角进行“多模切换”估计，保证系统状态突变时的良好估计精度。最后通过CarSim 和Simulink搭建联合仿真验证平台，对相关行驶状态的估计效果进行有效性验证。

1 车辆横向动力学PWA建模

1.1 车辆动力学模型

为尽可能考虑车辆横向运动的关键因素，并保持一定的模型简洁性，本文首先构建车辆2 自由度横向动力学模型。车辆的俯视图如图1 所示。在此基础上，2 自由度车辆横向动力学模型可表示如下［15-16］：

图1 车辆2自由度横向动力学模型

式中：m和Iz分别为整车质量和横摆转动惯量；vx、vy和γ分别为车辆纵向速度、横向速度和横摆角速度；δ代表车辆的前轮转角；Fyfl、Fyfr、Fyrl和Fyrr（式中 “fl”、“fr”、“rl”和“rr”代表了左前轮、右前轮、左后轮和右后轮）代表了4 个车轮的侧向力；lf、lr、l和B分别表示车辆的前轴距离、后轴距离、轴距和轮距。

轮胎的侧向力是由轮胎侧偏特性决定的，鉴于本文拟采用PWA 辨识方法进行轮胎侧偏力学特性建模，因此，轮胎侧向力可通过分段仿射形式表示为

式中：αfl、αfr、αrl和αrr为轮胎侧偏角；Cr代表后轮的侧偏刚度；Fzfl和Fzfr为左前轮和后前轮的垂直载荷；μ为路面附着系数。在紧急转向等特殊行驶工况下，前轮侧偏角变化相对较大，轮胎侧向力与其影响因素（侧偏角，垂直载荷，附着系数）间表现出高度非线性，因此采用PWA 辨识方法进行轮胎侧偏力学特性建模，而后轮的侧偏角通常变化幅度较小，此时轮胎侧偏力学特性往往处于线性区域内，故而轮胎侧向力可用侧偏角与侧偏刚度的乘积来表示。

基于车轮动力学分析，轮胎侧偏角与其他状态参数间的数学关系［17］可表示为

垂直载荷对轮胎侧偏特性也有显著影响，车辆转向过程中的垂直载荷变化可表示为

1.2 轮胎侧偏特性分段仿射辨识

本文通过试验获得能够反映轮胎非线性侧偏力学特性的原始数据，并在此基础上实现轮胎侧偏力学特性模型的PWA 辨识。图2和图3给出了两种路面附着系数下的轮胎侧偏力学特性试验结果，图中相关数据已进行滤波去噪和拟合处理。从图中可以看出，轮胎侧向力与其影响因素间的数学关系呈现出明显的非线性，因此，本文通过PWA 辨识方法进行轮胎非线性侧偏力学特性建模。

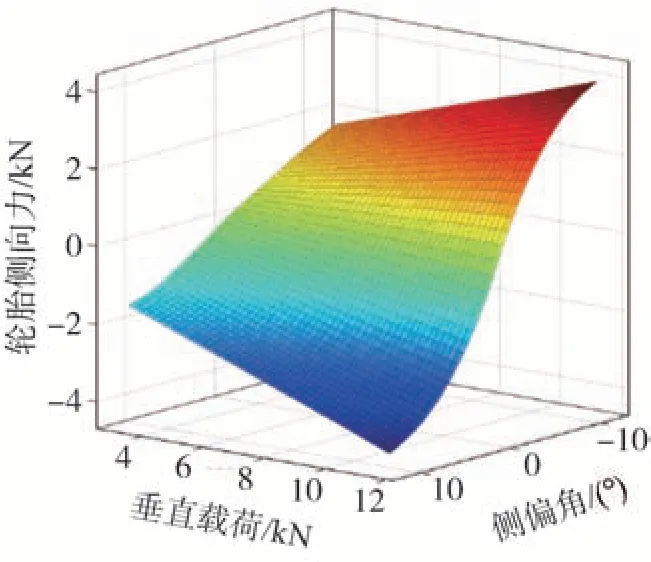
图2 低附路面轮胎侧偏特性试验结果（μ=0.34）

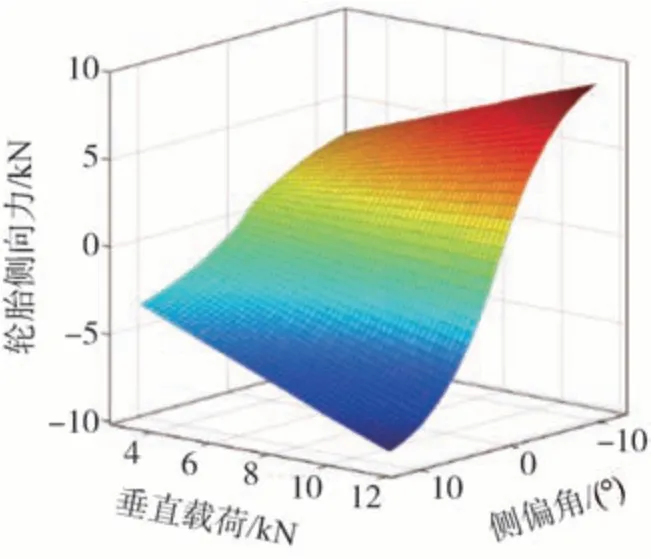
图3 高附路面轮胎侧偏特性试验结果（μ=0.77）

一般的，PWA系统可以被表示为

式中：y（k）代表PWA 系统的输出；θi（i=1，…，s）表示每个仿射子模型的参数；s为仿射子模型数量；φ（k）为回归向量；χi（i=1，…，s）为回归集χ的完整分区，每一个区域χi是一个凸多面体。

式中Fi和gi为分界面系数矩阵。

基于上述方程，轮胎侧偏力学特性的PWA 辨识主要涉及数据聚类、仿射子模型参数估计和分界面系数矩阵求解等3 个步骤，可通过不同算法实现。具体步骤如图4所示。

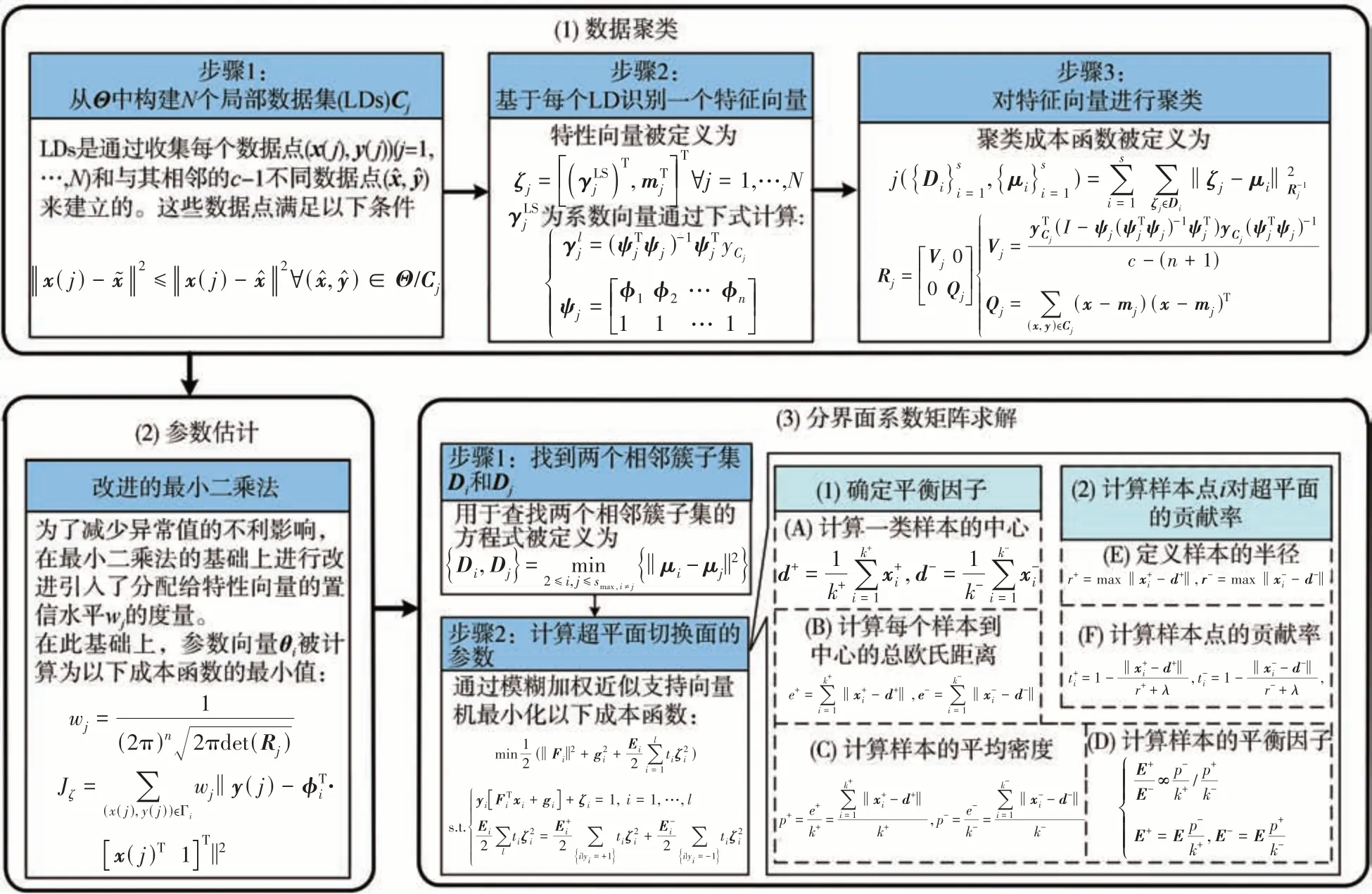
图4 轮胎侧偏力学特性分段仿射辨识的主要步骤

首先，在数据聚类中采用改进的K-means算法，图中显示了其主要步骤［18］。图中，Θ是原始数据集，是根据Cj中数据点估计的系数向量，φi（i=1，…，n）是属于Cj的回归向量，yCj是Cj中输出样本向量，mj是用于测量Cj中数据点稀疏性的散射矩阵，μi是不相交子集Di的中心，Rj是方差矩阵用于反映γj是通过使用属于单个子模型的数据点得出的置信度，Vj是经验协方差矩阵，Qj是测量Cj中数据点稀疏性的散射矩阵。其中n=ny+pnu，ny和nu是PWA 模型阶数，p是PWA 系统输入向量的维数。聚类算法的目标是找到最小化代价函数J的子集Di和中心ui来达到数据聚类的目的。

其次，在参数估计中可以基于数据集中收集的数据点对第i个仿射子模型进行参数估计。考虑到传统最小二乘算法因分类误差可能会对异常值敏感，因此，本文使用加权最小二乘算法［19］。

最后，分界面系数矩阵的求解可归结为通过线性分类器解决s（s-1）/2 模式的识别问题。根据统计学习方法原理，解决这一问题的可行方法是采用支持向量机（SVM）算法。考虑到大量数据点和计算效率要求，本文中采用模糊加权近似支持向量机（FPSVM）算法［20］。图中，ζi为用于防止样本数据在相邻子集中线性不可分的松弛变量，l是相邻子集中的数据点数量，Ei用于确保算法复杂度和误分类样本数量之间良好平衡的样本数据的平衡因子，ti是用于表示样本数据i对超平面的贡献率的变量。当ti越小，样本数据对超平面的影响越小。为了实现成本函数最小化的解决方案，拉格朗日方程被构造进行求解进而得到超平面系数矩阵。

轮胎侧偏力学特性PWA 辨识的具体步骤描述可参照研究团队前期发表的论文［21］。PWA 模型辨识出的仿射子模型结果如表1所示。PWA侧向力模型与试验数据之间的误差如图5 所示。从图中可以看出，本文建立的轮胎PWA 模型具有较高的精度，拟合误差集中在零附近，能够有效反映轮胎的非线性侧偏力学特性。

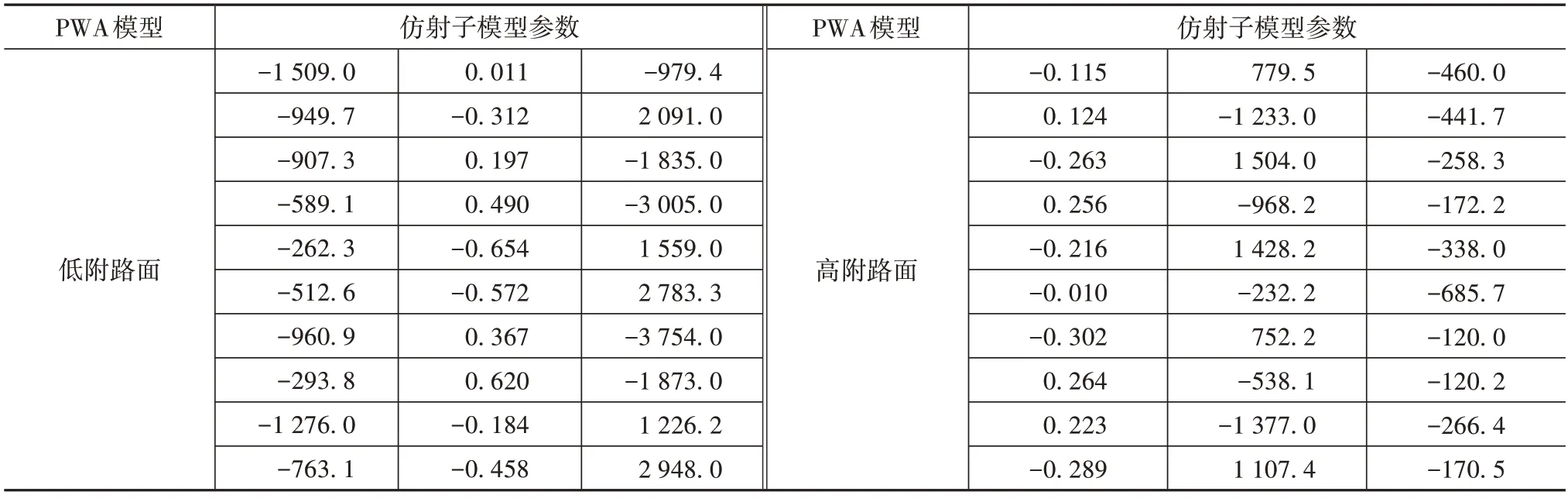
表1 仿射子模型参数

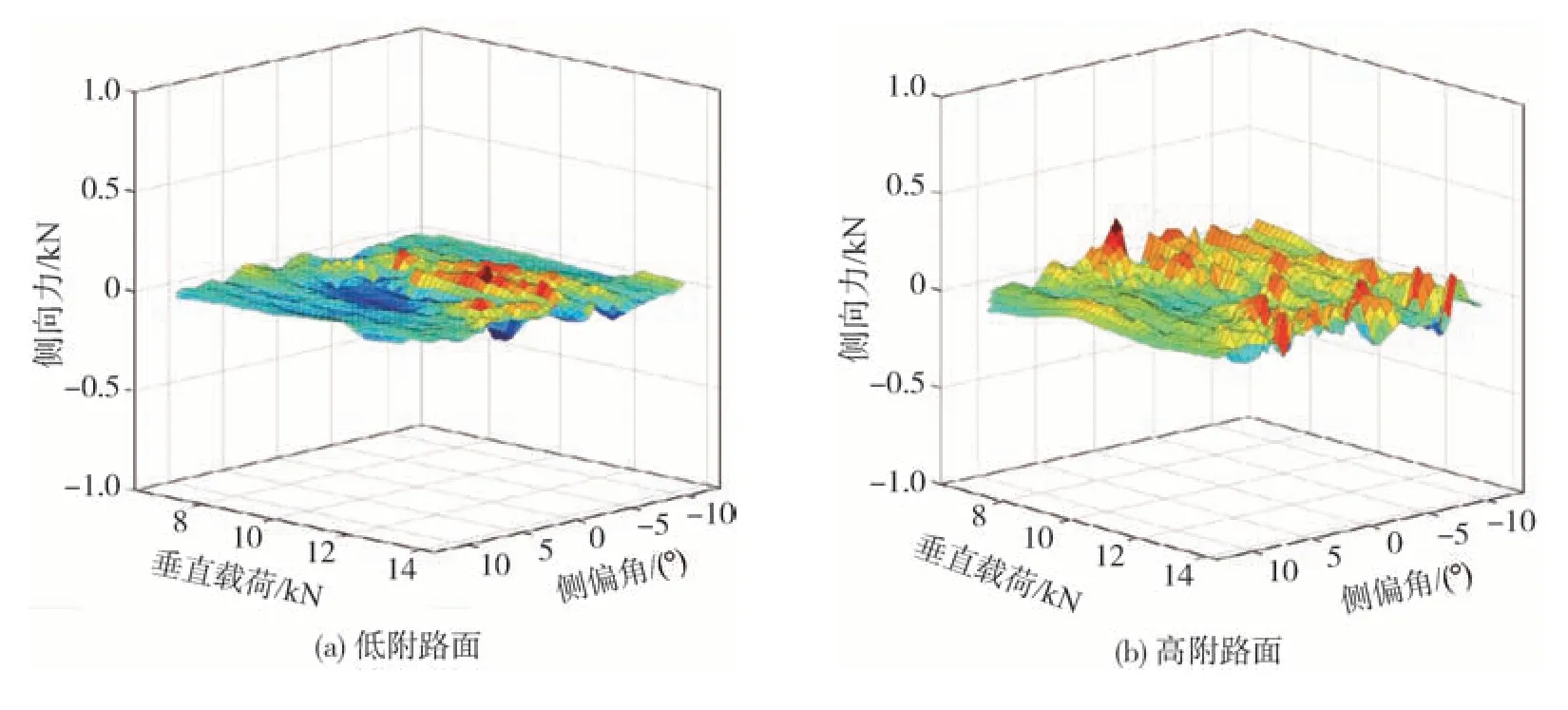
图5 PWA轮胎模型与试验数据的误差

2 行驶状态估计策略设计

2.1 基于PWA模型的非线性状态方程

在轮胎非线性侧偏力学特性PWA 辨识的基础上，本文中建立了汽车横向动力学PWA 模型。该模型是由多个仿射子模型组成，且子模型的切换主要由轮胎侧偏角和垂向载荷所决定。基于该前提，本文所设计的车辆行驶状态估计框架如图6所示。

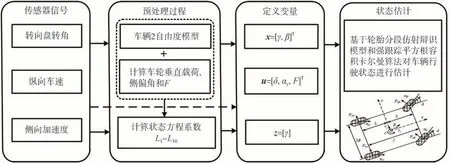
图6 车辆行驶状态估计算法框架

轮胎侧向力的表达式进一步简化为

通过对车辆动力学进行分析，车辆质心侧偏角［22］可表示为

结合式（1）和式（8），非线性系统状态方程表示为

状态向量定义为

输入向量可被定义为

式中F代表轮胎纵向力对车身横摆运动的影响［23］，可表示为

测量向量可被定义为

状态方程和测量方程可被表示为

式中f（·）和h（·）的具体表达式为

式中L1-L10是在轮胎侧偏特性PWA 模型基础上，通过对车辆动力学进行建模得出的参数。通过在预处理过程中计算轮胎侧偏角α和垂向载荷Fz，即可判断出各车轮侧向力处于哪个仿射子模型区间，进而确定L1-L10的数值。

2.2 平方根容积卡尔曼滤波算法

考虑到以下的非线性离散系统：

式中：xk为系统的状态向量；uk为输入向量；zk为测量向量；f（·）和h（·）为状态方程和测量方程；wk和vk分别代表系统噪声和测量噪声，wk和vk的均值分别为q和r，协方差矩阵是Qk和Rk。标准的平方根容积卡尔曼滤波算法［24］如下。

（1）初始化

式中：P0|0为误差协方差矩阵；Chol（·）为Cholesky分解。

（2）时间更新

容积点和传递后的容积点的计算公式为

式中：Sk|k为Pk|k经过Cholesky分解的平方根因子，Sk|k=［Chol（Pk|k）］T；ξi为容积点权重矩阵的第i列，In为n×n的单位矩阵，n为状态量的维度。

（3）测量更新

容积点和传递后的容积点被更新为

计算测量的预测值及其新息协方差矩阵的平方根因子：

式中SR，k+1=Chol（Rk+1）。加权中心矩阵Yk+1|k被定义为

计算测量协方差矩阵和互协方差矩阵：

χk+1|k被定义为

卡尔曼增益为

更新状态变量和误差协方差矩阵的平方根因子：

2.3 强跟踪平方根容积卡尔曼滤波算法

为防止目标状态突变导致估计精度下降的现象发生，本文将强跟踪算法与SCKF 算法相结合构成强跟踪平方根容积卡尔曼滤波算法（STSCKF）。当直接引入强跟踪算法中的渐消因子时，由于对角元素不同，导致预测误差协方差矩阵不对称，使滤波精度降低［25］，为避免该情况，本文选择在其平方根中引入渐消因子来替代，并用即

式中ρ为遗忘因子，ρ=0.95［26］。在强跟踪算法中，Hk+1和Fk+1是测量方程和状态方程对状态变量的1阶偏导数：

预测误差协方差为

假设Qk是正定对称矩阵，则Pk+1|k可逆：

因此

在强跟踪算法中，预测误差协方差的求解如下：

3 联合仿真验证

为验证前述行驶状态估计策略在紧急转向等特殊行驶工况下的实际效果，本文中进一步应用CarSim 和Simulink 建立了车辆行驶状态估计算法联合仿真验证平台。CarSim作为一种被广泛运用的高保真车辆动力学仿真软件，其模型包含了27 个自由度，因此，相关状态数据可被作为车辆行驶状态的参考值。在此基础上，另一种基于SCKF 的估计策略被作为对比验证对象。联合仿真模型如图7 所示，初始估计状态矩阵为=[0，0]T。系统噪声和测量噪声协方差矩阵分别被设置为：Q=10-3⋅diag（1，1），R=10-3。均值q和r被设置为0.1。其中整车模型的参数如表2所示。

表2 整车主要参数

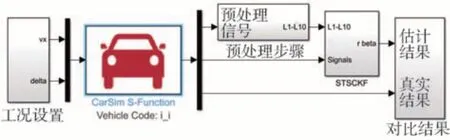
图7 CarSim-Simulink联合仿真模型

3.1 工况1：正弦转向工况

正弦转向工况中的转向盘转角如图8 所示，路面附着系数设置为0.4，车速保持72 km/h。图9 为两种估计策略的仿真结果与CarSim 中相关数据的对比以及状态估计过程中仿射子模型的切换行为。为便于进行对比分析，表3 还给出了两种估计策略下误差的峰值和均方根值。图9（a）为车辆横摆角速度的估计结果。从图中可以明显发现，相比于SCKF算法，本文采用的STSCKF 算法与CarSim 的结果更加吻合，呈现出更高的精度和更小的误差。图9（b）为湿滑路面上转向盘转角快速变化时质心侧偏角的估计结果。通过对比发现，未使用强跟踪算法时，状态估计误差明显增大。其中，横摆角速度峰值和质心侧偏角误差峰值分别增加了9.22（°）/s 和3.12°，误差均方根值分别增加了2.38（°）/s和0.72°。较大的误差使得车辆在进行横向稳定性控制时不能准确把握真实运行状态，从而导致控制结果不理想。如图9（c）所示，当车辆处于不同状态时，本文提出的轮胎侧向力PWA 模型会在不同仿射子模型间进行切换以达到更好的估计效果。综上，本文提出的STSCKF算法有着更高的估计精度和稳定性，为后续车辆的轨迹跟踪和横向稳定性控制奠定了重要基础。

表3 两种工况下两种策略的估计误差

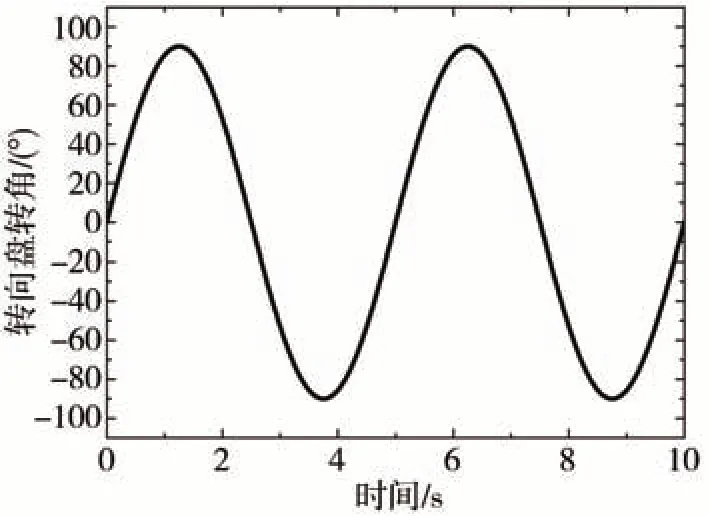
图8 转向盘转角

图9 正弦工况下的估计结果对比

3.2 工况2：J turn工况

本文所采用的第2种对比工况为Jturn工况，该工况下的转向盘转角变化和车速变化如图10 所示，路面附着系数设置为0.4。

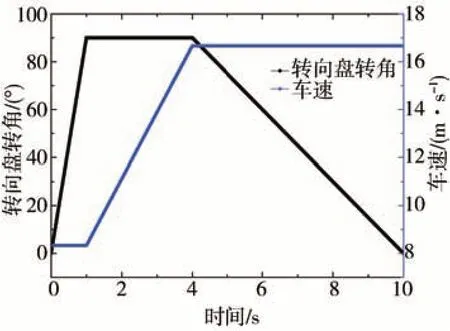
图10 J turn工况

图11 为两种估计策略对车辆横摆角速度和质心侧偏角的仿真结果以及仿射子模型的切换行为，相应误差的数据对比如表3 所示。由图11 和表3 可以看出，本文提出的STSCKF 估计算法相比于SCKF算法有着更高的估计精度。当车辆匀速行驶时，两者误差都保持较低，但是当车速和转向盘转角突变时，SCKF 算法的误差会明显增大，相比之下，STSCKF 算法依然能准确估计车辆的行驶状态。其中，横摆角速度和质心侧偏角的峰值误差分别减小了4.3（°）/s 和0.77°，误差均方根值分别减小了0.06（°）/s 和0.12°。以上结果表明，在全工况中，本文提出的估计策略可以快速收敛至系统实际状态，具有更好的估计速度和估计精度，从而验证了本文提出的STSCKF 算法的有效性和实用性。与此同时，在车辆行驶过程中，前轮垂向载荷不断变化，本文提出的轮胎PWA 模型可以在不同仿射子模型中进行有效切换，保证了车辆系统模型的精度，从而为达到更好的估计效果奠定了重要基础。