封装工艺对电枢热导率影响的实验研究*

李兆宗，张承宁，章恒亮，张 硕

（1.北京理工大学机械与车辆学院，北京 100081；2.东南大学电气工程学院，南京 210096；3.诺丁汉大学电气工程学院，英国 诺丁汉 NG7 2GT）

前言

近年来，随着电动车驱动技术的多样化发展，在集中驱动结构中应用的高转速电机［1-2］和在轮毂电机结构中应用的高转矩电机［3-4］同时成为汽车领域广泛应用的电机类型。因此，在传统圆形漆包线绕组的基础上，发卡绕组（扁铜线）和绞线绕组电机同时孕育而生。发卡绕组的优势在于可以降低电机在低速工况下的直流损耗［3］，能够有效提高电机在低速工作区间的工作效率。反之，绞线绕组应用的目的是通过缓解电枢中的趋肤效应和临近效应以降低电机的交流损耗［4-5］，从而提高电机在高转速工作区间的工作效率。常见的绞线电枢主要包括换位漆包线、圆形利兹线和矩形利兹线等结构。

相对于应用在静态电力电子设备（如变压器、电磁炉等）中的电枢结构，车用电机最显著的特点在于其电枢大多具有封装工艺，即通过对电枢灌注环氧树脂等高性能非金属材料以保证电机定子的结构强度和可靠性。图1 所展示的电枢为封装后的利兹线电枢。本文设定图中z轴方向为电枢轴向，x、y为电枢的截面方向。

电机电枢的热管理是提高车用电机性能的关键，也是保障电机可靠性的基础。因此，准确计算电枢的热导率是建立模型必不可少的前期工作。在此，为评估各类计算车用电机电枢热导率方法的优势和局限，文中汇总了国际上10 篇有代表性的文献以便读者参考，如表1所示。

表1 车用电机各类电枢热导率计算方法汇总

通过对表1中文献的总结，可以得出目前电机设计者对电枢轴向热导率预测存在的如下3点局限。

（1）各向异性研究不充分 各类电枢的轴向热导率研究不如截面方向的热导率研究充分，轴向热导率普遍采用经验参数或电枢的填充密度作为估算电枢轴向热导率的依据。然而，由于高频电机中的电枢通常会具有独特的绞合结构，封装工艺对其传热效率的影响也将比传统圆形绕组更加明显，须仔细考虑。

（2）模型精度不足 包括换位漆包线和利兹线在内的绞合电枢的热导率解析计算结果误差在10%以上，仍有一定的优化空间。同时，随着电机种类的多样化，端部油冷电机以及轴向磁通电机应运而生［4-5］。在这些电机的拓扑结构中，其电枢中大部分的热量都是通过轴向散发，因此须对电机建立三维模型才能得到更精确的预测结果。然而，面对复杂的绞合电枢结构，传统的轴向热导率估算方法是无法满足精度要求的。

（3）工艺考虑不足 各类电枢轴向热导率的模型均未涉及封装工艺对电枢传热特性的影响。然而，在日益提升的非金属材料导热性质面前，直接忽略非金属材料的热导率不够严谨。上述文献中所有的模型均无法表达电枢内部漆包线之间的传热性质，所以很难在模型中体现出电枢在封装后的热导率变化，这种直接忽视封装工艺的计算方法在车用电机中需要得到更新。

因此，本文提出一种能够表达车用电机电枢轴向热导率的数学模型，并能够得到电枢在封装后更加精确的热导率。然而，由于目前没有评估封装工艺对热导率影响的文献能够作为参考，所以本文选择从实验的角度出发，首先通过实验数据得到电枢真实的物理性质，而后通过对电枢的结构特点和实验数据分析对其建立相应的数学模型，以保证高效准确地实现各类电枢轴向热导率的预测。

1 各类电枢的结构特点

选取的9款电枢样品如图2所示，其关键参数的详细信息汇总在表2中。

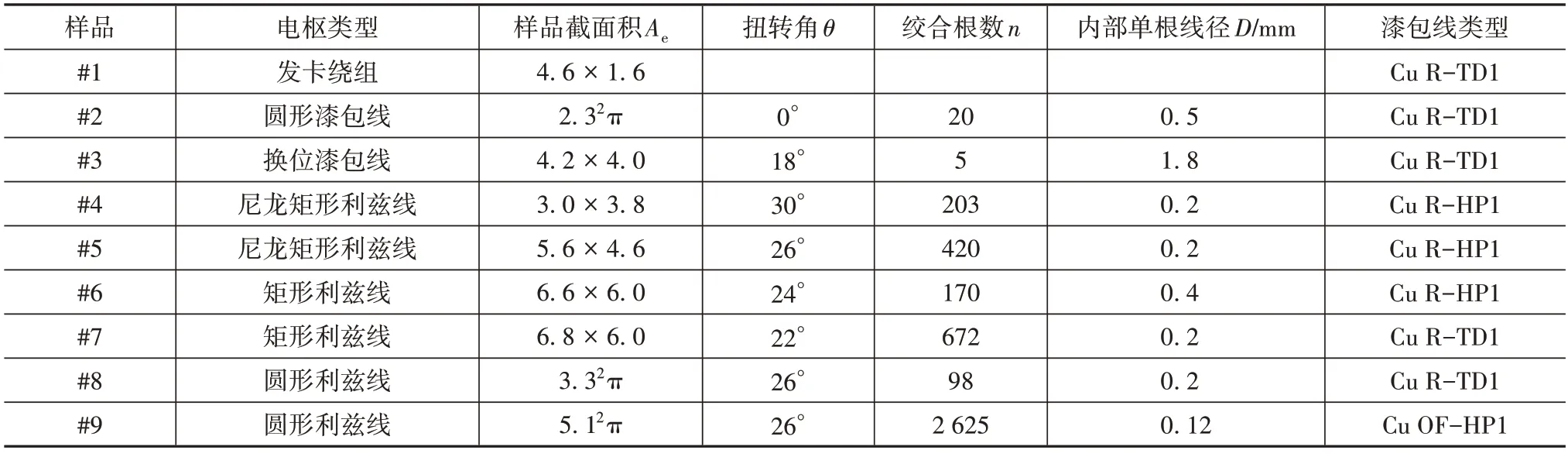
表2 样品信息

图2 电枢样品

在表2 中，电枢类型是指其加工工艺带来的不同性质。目前市面上应用的电枢主要包括绞合和塑形（压缩）两种加工工艺。电枢的绞合通常会经历1～3 次，根据漆包线绞合次数的不同，它们分别被称为“换位漆包线”、“利兹线”和“多层利兹线”。同时，为实现更高的槽满率，各类电枢也会被压缩为适用于各类电机的矩形截面。其工艺流程以及样品#1～#9所归属的类型如图3所示。

图3 各类电枢的加工流程

电枢的截面积Ae如图3 中的虚线框所示。电枢中的扭转角θ为各类绞线的扭转角，其物理意义如图4所示。

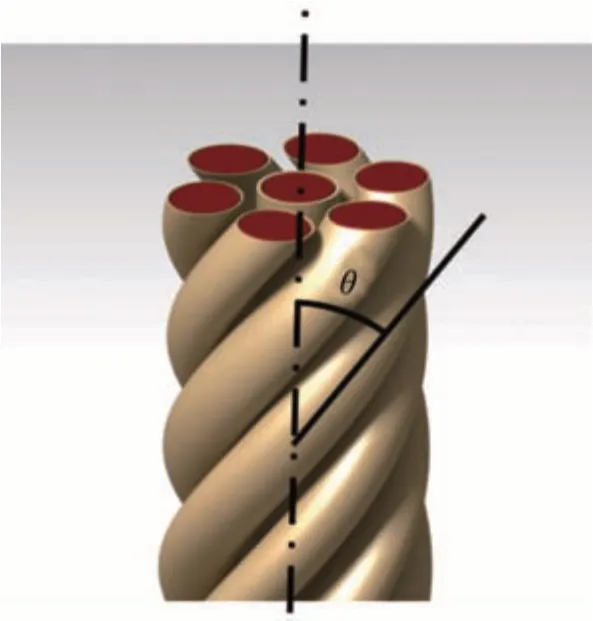
图4 电枢的扭转角θ

绞合根数n和单根线径D指的是绞线内部漆包线的总数和单根漆包线的直径。漆包线类型中涉及的漆包线与封装材料的物理性质均来自于样品的参数表，本文中所需的材料信息汇总于表3。

表3 材料热导率信息

值得注意的是，为更好地复现封装材料对电枢热导率的影响，文中使用目前车用电机最常见的非金属固化剂［Epoxylite 235SG］作为各类电枢的灌封材料，以更好地对比封装工艺对电枢热导率的影响。文中所有电枢样品的封装工艺均模拟车用电机标准，在施加预紧力的条件下进行真空浸渍（vacuum casting），从而改善电枢内部漆包线之间的接触条件，增强换热效率。以样品#4 为例，真空浸渍后的电枢样品如图5所示。

图5 封装后的样品#4

2 轴向热导率测定实验

面对电枢多样化的内部结构，设计者通常很难直接建立导体内部的传热模型，更难以直接通过解析计算评估封装工艺对各类电枢热导率的影响。为提高建模效率，首先对封装前后的电枢的轴向热导率进行测量。

2.1 实验台架设计

电枢轴向热导率的实验台架原理如图6所示。

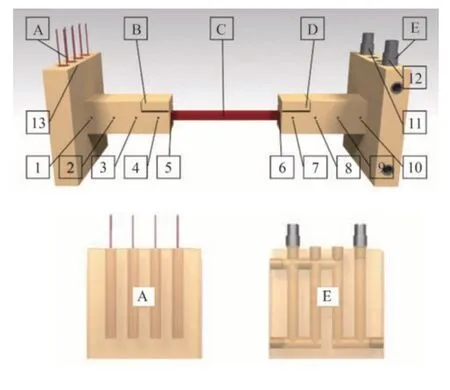
图6 样品测量原理

图中A 为嵌有加热器的铜板，用恒定的热源控制温度。夹具B 和D 用来固定电枢样品C，夹具B 和夹具D 的形状相同。E 为内部有冷却液通道的铜板。台架中部件A、B、D 和E 均使用铜［HC101］制作而成。点1～13 为测温通道。通道1、2 和3 之间的温差可以用来计算流经B 的热流qB，通道8、9 和10 可以用来计算流经D 的热流qD。通道4 和6 的温度可以用来检查样品与B 之间的接触。通道5 和通道6用来获取样品C 两段的温度差，从而计算出通过样品的热流密度。通道11 和12 分别对应冷却剂进口和出口温度，用于监测冷却液的实时温度。通道13用来测量热板A的温度和PID恒温热源的功率控制。

在热稳定条件下，流经B 的热流密度qB应等于流经D 的热流密度qD，且与流经C 的热流密度qC相同。计算样品轴向热导率的方法为

式中：AB和Ae分别为夹具B 和待测样品C 的截面积，mm2；λCu为铜［HC101］的热导率，W/(m·℃)；ΔTi，j为i点与j点之间的温差，℃；Δxi，j为i点与j点之间的物理距离，mm；λSample为每个样品中待测热导率，W/(m·℃)。

基于上述原理，实验在样品和实验台上包裹了绝热层，缓解样品向外界的散热。实验台表面覆盖的隔热层为钙镁硅酸绝热片，最外层为泡沫箱。成品实验台和温度采集器如图7所示。

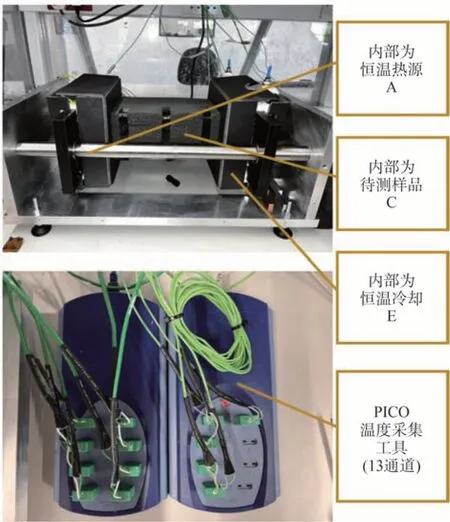
图7 实验设备实拍图

2.2 实验台架的误差标定

由于需要讨论封装工艺对各类电枢的未知影响，所以实验台架的测量值需要较高的精度，以保证后续分析的有效性。

基于上述的实验原理，热导率测量的误差将来自两个方面，一个是热电偶的测量误差，另一个是实验台之间的散热。因此，首先对式（2）热导率计算式进行改写，并引入两个修正系数kd和δij作为台架补偿系数，公式为

式中：kd为台架的散热补偿系数；δij为热电偶误差补偿系数。

台架的误差补偿系数kd须通过建立散热模型进行计算，如图8所示。

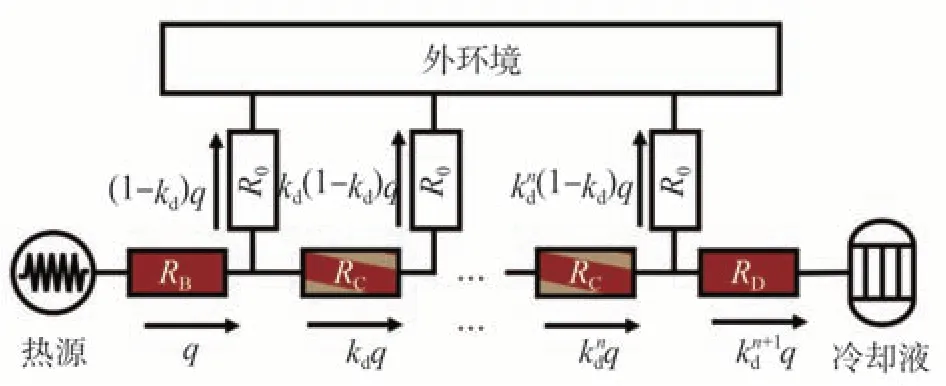
图8 实验台架的散热模型

图中RB、RC、RD和R0分别代表夹具B、样品C、夹具D 和绝热层的热阻。假设实验台架可划分为n段，每段的绝热条件相同，且外部环境温度一致。则可以假定的热量继续沿导体传递，而的热量则向外传递。因此，为求解上述未知数kd，需要使用多个性质已知的样品作为标定。校准过程中，分别使用200和150 mm的铜［HC101］（热导率为391 W/（m·℃））和铝合金［HE30TF］（热导率为180 W/（m·℃））金属条作为标定样品，以保证所有的利兹线样品的热导率经验值范围均处于391～180 W/（m·℃）之间，如图9所示。

图9 标定样品

对于每个标定用的样品，台架分别将A 铜板设置为50、70、90 ℃ 3 个温度，E 铜板保持在10 ℃，并在上述条件下重复多次测量通过qB和qD的差值，依据图8 中的散热路径图求取平均值后计算台架的散热系数kd。

热电偶的误差补偿系数δij通过热水浴进行标定。其具体方法为：分别记录下通道1～4处于i温度条件时各热电偶的误差δi，以及通道8～10处于j温度条件下各热电偶的误差δi，从而得到夹具上8根热电偶在加热端温度为i、制冷端温度为j条件下的误差δij作为后续计算的热电偶补偿系数，如图10所示。

图10 热电偶的水浴标定

在得到实验台架的kd和δij两个补偿系数后，再次参照上述实验条件测量图11 中100 mm 的两个标定样品。

图11 标定样品

图11 中铜条样品在点1～10 的温度收集结果如图12（a）所示，铝条样品在点1～10 的温度收集结果如图12（b）所示。铜条和铝条热导率计算结果如表4所示。

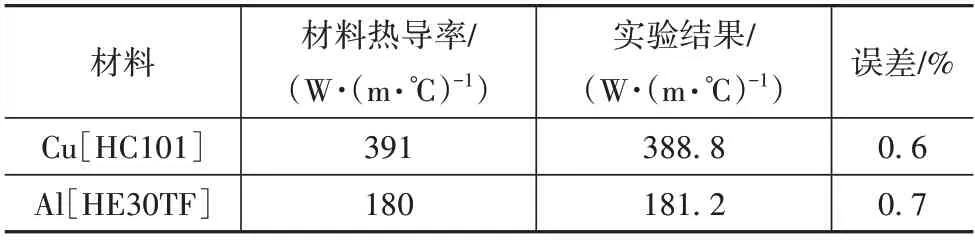
表4 台架标定结果

图12 标定样品温度采集结果

通过对标准材料Cu ［HC101］和Al ［HE30TF］样品的标定，在后续测量100 mm 样品的实验中，实验台架展示出良好的准确性。通过表4 可以看出，该实验台的误差可以将待测样品的导热系数误差控制在0.7%以内，具有足够的参考价值。

2.3 测量结果

在标定实验台架后，该实验台配合补偿系数测得9 个样品在封装前后的热导率，并计算得到封装工艺对其热导率产生的影响。在验证过程中，冷却液温度固定在10 ℃，A 的温度控制在50、70、90 ℃3 个不同的温度。同时，实验过程中，为保证各个样品测量结果的准确性，每款电枢均加工了多个样品，且测量时会将样品的“加热端”和“制冷端”调换一次，分别记录两次的温度梯度数据，以消除样品两端可能出现的尺寸差异。实验结果如表5 所示，并绘制如图13所示的柱状图作为更好的参考。

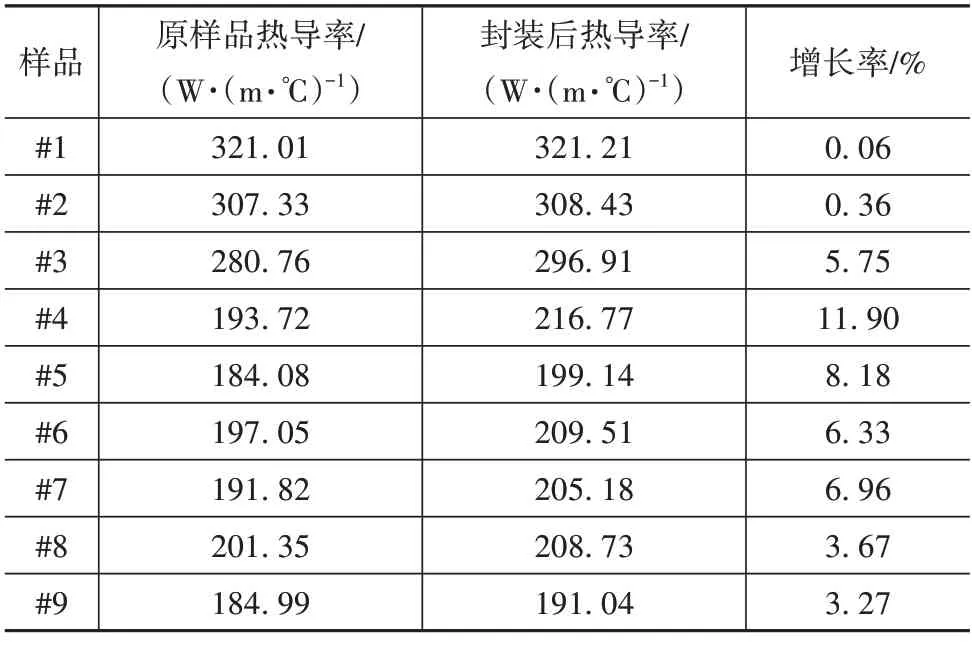
表5 实验结果

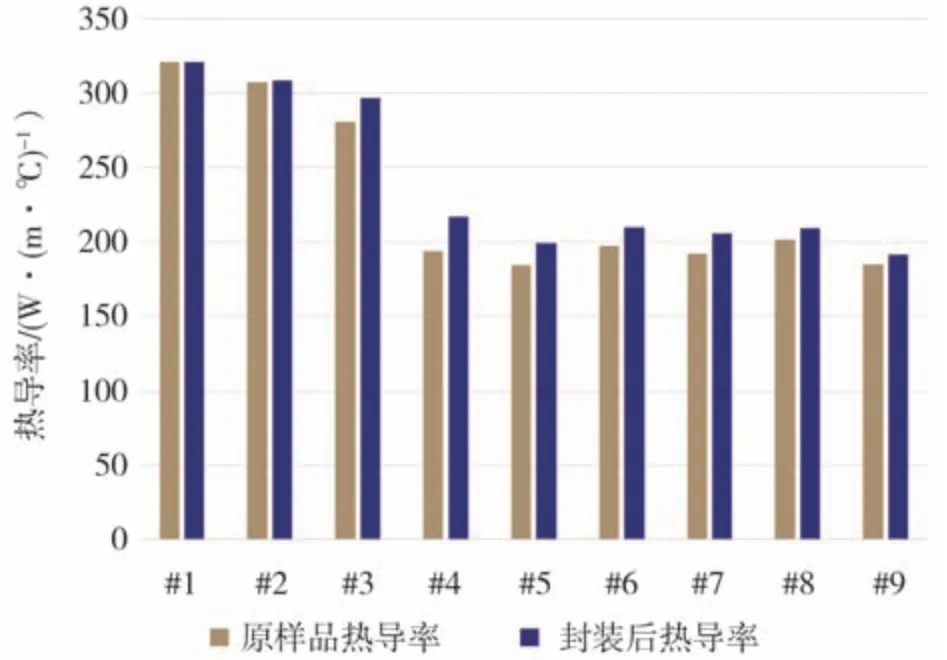
图13 样品封装前后热导率对比

通过对各类电枢封装前后热导率的对比，可以发现非金属封装材料对电枢轴向热导率起到的影响不能忽视。但是，对于样品中的发卡绕组和圆形漆包线而言，其影响相对较小。反之，对于包括换位漆包线和利兹线在内的各类绞线的影响却非常明显。基于对实验结果和传热理论的分析可知，圆形绞线是可以通过塑型工艺提升其轴向热导率。其原因在于，塑形改变了漆包线之间的接触情况，在微观层面提升了各根漆包线之间的接触面积，从而使电枢对真空浸渍工艺更加敏感。

3 封装工艺影响的建模分析

对于实验数据所展示出的两种不同性质，将电枢样品分为“平行电枢”和“绞合电枢”两类，并基于其内部结构提出了两种计算电枢轴向热导率的方法。

3.1 平行电枢轴向热导率模型

平行电枢（parallel winding）是指电枢内部的漆包线平行排列，不存在绞合工艺，主要包括发卡绕组和圆形漆包线等电枢种类。对于这类电枢，封装工艺对其热导率的影响来自轴向，即漆包线和封装材料的热导率处于并联状态，槽内的材料分布如图14所示。

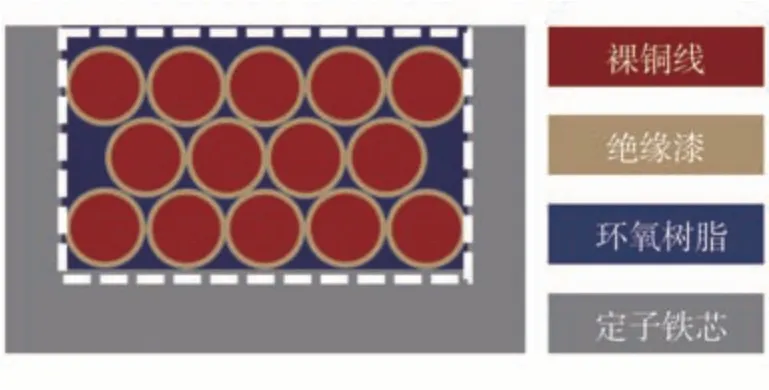
图14 平行电枢槽内材料分布

图中白色虚线框指齿槽截面积AS。因此，平行电枢的等效热导率并联模型如图15所示。

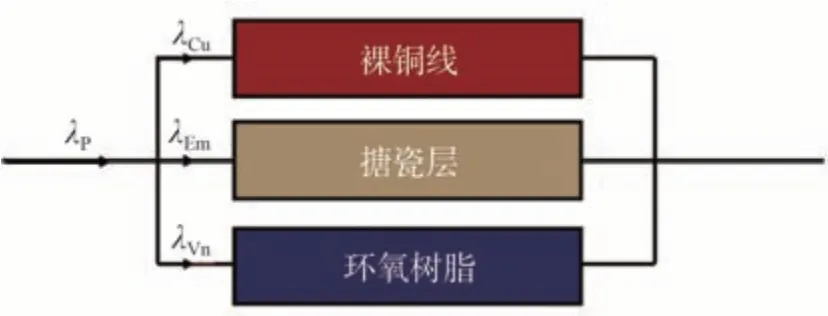
图15 平行电枢热导率模型

平行电枢的等效热导率λP计算公式为

式中：λCu、λEm和λVn分别代表铜、漆包线搪瓷层和封装材料的热导率，W/(m·℃)；AS为齿槽截面积；ACu、AEm和AVn分别代表齿槽内部各种材料的截面积，mm2。模型中各材料热导率均已知，因此只须知道各类材料在电枢内的体积占比即可获得电枢的轴向热导率：

式中：ff为电枢的槽满率，可直接通过齿槽截面积和电枢的数量确定；σ为搪瓷层厚度相对漆包线中裸铜线直径的比值，目前标准漆包线和发卡绕组的σ取值均为0.05。因此，平行电枢的槽内热导率λP可以将σ代入式(4)后通过各材料占比计算，公式为

3.2 绞合电枢轴向热导率模型

绞合电枢（twisted winding）是指将电枢内部的漆包线进行扭转后制成的电枢，主要包括换位漆包线和利兹线等结构，其理想化的三维模型如图16所示。

图16 绞合电枢的理想结构

不难看出，无论是矩形绞线还是圆形绞线，各层导体在绞合后均呈现出平行状态。因此为简化模型，可以将一小段三维模型中的绞线模型展开，简化为平形排布的电枢模型，从而构建微观层面的传热模型，如图17所示。

图17 展开后的绞线模型

基于热传导规律，由于封装材料的热导率远小于铜线内部的热导率，因此封装工艺的影响主要作用于漆包线之间的传热。相对于平行电枢结构，绞合后的电枢内部传热路径不能直接以并联关系进行计算。从微观角度来看，绞合后的电枢内部出现漆包线之间的叠压关系。在微观模型中可以得到漆包线之间的传热与裸铜线中传热的几何关系，其微观传热路径如图18所示。

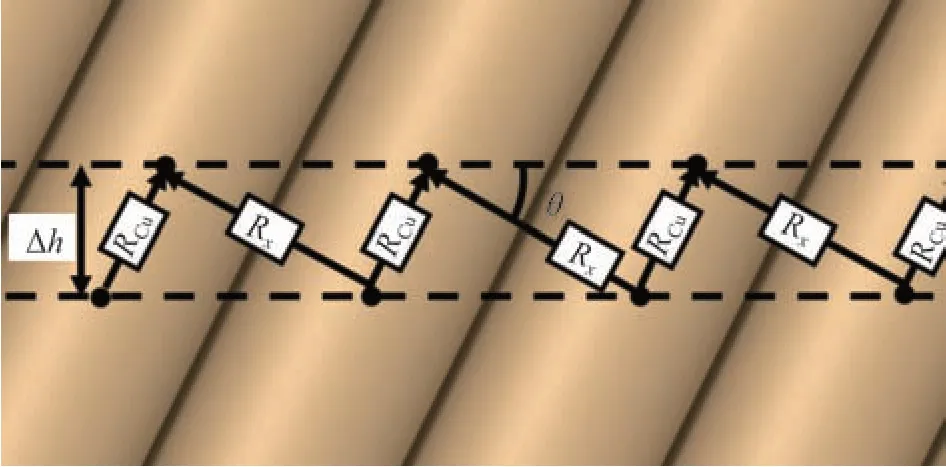
图18 绞合电枢内部传热路径

图中：Δh为一小段电枢长度；RCu为裸铜线的热阻；Rx为漆包线之间的热阻，其等效热阻的计算公式见式（9）。

式中：RT为绞合电枢热阻，m2·℃/W；RCu为裸铜线热阻，m2·℃/W；Rx为漆包线之间的热阻，m2·℃/W。根据傅里叶传热定律，可对热导率计算中所需的物理量建立几何模型，如图19所示。

图19 热导率计算中物理量的几何关系

图中：θ为电枢的扭转角度；Δh为高温面和低温面之间的距离，mm；l1为电枢从高温面向低温面传热时，热流在裸铜线中的传热路径长度，mm；l2为叠压漆包线之间的传热路径长度，mm。其计算公式为

图中：A1为裸铜线的传热面积，mm2；A2为漆包线之间传热的等效面积，mm2。其计算公式为

在明确上述物理量的计算方法后，Δh长度的绞合电枢热阻计算公式为

绞合电枢的热导率λT的计算公式为

式中AE为电枢样品的截面积，mm2。

由于上述Rx和λx为漆包线叠压后各导体之间的未知热导率，无法直接通过材料性质获得，因此须通过实验结果进行求解，并对结果进行分析。通过绞合电枢样品#3～#9的实验数据，可以在代入式(19)后解得λx。同时，由于绝大多数车用电机电枢均采用铜线，其物理性质有较好的一致性，所以可以将λx的主要影响因素归结为加工工艺造成的差异，所以对于具有不同工艺的电枢结构求取平均值计算经验系数是有意义的，其结果如表6所示。

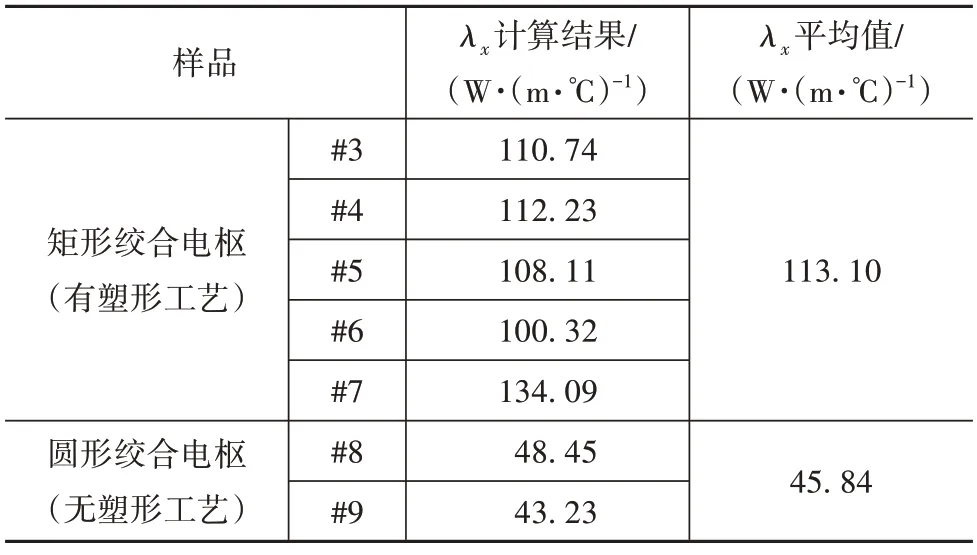
表6 λx计算结果

通过表6 可进一步将绞合电枢分为两类，其一是具有塑形工艺的矩形绞线，其二是不具有塑形工艺的圆形绞线。计算结果表明，矩形绞线在封装后之所以在漆包线之间有更好热导率，其原因在于矩形线在绞合完成后会首先经过一次塑形挤压，在施加一定预紧力制成电枢后会产生更紧凑的结构，因此封装工艺对其热导率的影响也会更显著。但值得注意的是，该经验值只能表达浸渍电枢内部微观的传热行为规律，而不能代表电枢整体的截面方向热导率。

3.3 模型的意义

经过前文对实验结果的分析，表明封装工艺对于绞合电枢的热导率影响非常明显。同时，对于平行电枢和绞合电枢的数学模型分析也证明了封装工艺对电枢槽内热导率的影响权重。

基于式（8）中的计算方法，计算平行电枢样品#1和#2的轴向热导率结果如表7所示。

基于式（19）的计算方法与表6 中得出的漆包线内部传热经验系数，计算绞合电枢样品#3～#9 的轴向热导率结果如表8所示。

表8 绞合电枢封装后热导率预测结果

综上所述，通过将表6 中的结论代入式（8）与式（19）的数学模型可以得到电枢的轴向热导率一般估算方法。

平行电枢：

非塑形绞合电枢：

塑形绞合电枢：

上述结论解决了包括发卡绕组、圆形漆包线、换位漆包线、矩形利兹线和圆形利兹线在内的几乎所有车用电机电枢的轴向热导率估算问题。上述模型可使电机设计者凭借电枢的结构信息即可计算出电枢在封装后所表现出的温度服役行为，有效地简化了表1 中文献所使用的等效模型和等效介质理论等数学方法。同时，上述模型的提出可以将绞合电枢轴向热导率的预测误差控制在1.1%以内，对于现有文献中的温度预测结果也是明显进步。另一方面，该模型的提出也表明绞合电枢在应用过程中使用塑形工艺能够有效提升其轴向热导率这一现象。

4 结论

为满足各类电动车辆驱动结构的性能要求，多样化的电枢被应用在驱动电机中。而封装工艺对各类电枢的影响在车用电机的温度预测中是不可忽略的重要影响因素。选取9 款有代表性的电枢结构，测量了其封装后电枢的热导率，并将其归纳为“平行电枢”和“绞合电枢”两种结构类型进行建模分析。通过实验结果与建模分析可知，封装工艺对包括换位漆包线和利兹线在内的“绞合电枢”的轴向热导率有明显提升作用。基于上述性质，本文对两类电枢分别建立等效热导率模型，并求解绞合电枢内部叠压漆包线之间的传热效率。计算结果表明，封装工艺对具有塑形工艺的矩形绞线的热导率有最显著的提升作用，圆形绞线次之。最后，通过经验模型能够合理地预测各类电枢的轴向热导率，其计算误差在1.1%以内。