基于交互式多模型卡尔曼滤波的主动悬架控制*

吴 骁，史文库，陈志勇

（吉林大学，汽车仿真与控制国家重点实验室，长春 130022）

前言

悬架是汽车行驶系统的重要组成部分，汽车运行时，高低不平的路面通过车轮输入悬架系统，造成悬架振动，影响汽车的平顺性与操纵稳定性。为了提高悬架在各种路面上的振动特性，近年来一种基于智能算法的路面自适应悬架逐渐成为研究热点。路面自适应悬架是指悬架可根据路面高程值及自身振动方式的改变合理地调整状态参数，使悬架振动特性达到最优［1-3］。在汽车悬架控制系统中，状态观测起着重要作用［4］。状态观测指通过传感器及算法合理地测量系统状态［5-6］。一个精确的、鲁棒的悬架状态观测器对汽车的平顺性、安全性等特性有着重要的影响［7］。鉴于状态观测的成本与精度之间的矛盾，如何根据系统特性合理地选择、设计状态观测器逐渐成为状态观测研究的核心［8］，其中，基于卡尔曼滤波的悬架状态观测是最常用的且精度较高的一种状态观测策略［9-12］。

近些年来对于基于卡尔曼滤波的悬架状态观测的研究可分为基于固定观测器固定状态方程的状态观测、基于固定观测器可变状态方程的状态观测和基于可变观测器可变状态方程的状态观测，其中基于可变观测器可变状态方程的状态观测是研究的热点。对于基于固定观测器固定状态方程的状态观测，文献［9］中基于簧载质量垂直加速度进行道路分类，利用道路分类结果确定系统的状态方程，将状态方程与对应的KF 相结合完成系统的观测。对于固定观测器可变状态方程的状态观测，文献［10］中建立了一种基于主动悬架的卡尔曼滤波状态观测器，通过道路条件变化及车身质量改变建立不同的状态方程，利用卡尔曼滤波器对系统状态进行观测，对比了状态方程的改变对系统观测精度的影响。对于可变观测器可变状态方程的状态观测，文献［11］中综合分析了不同路面激励水平下Q与R的关系，采用一种基于簧载质量加速度和非簧载质量加速度的新型道路分类方法，准确获取了车辆系统的Q，提出一种AUKF 方法，通过道路识别确定系统状态，验证了所提出的AUKF 方法在不同路面激励条件下能够准确估计车辆状态。文献［12］中考虑簧载质量在不同运动条件下的变化，提出了一种无迹卡尔曼滤波（UKF）算法来识别簧载质量。基于交互多模型（IMM）和马尔可夫链蒙特卡罗（MCMC）理论，提出了一种新型的IMMUKF观测器来估计悬架系统的运动状态。利用C 级路面与E 级路面的仿真验证了模型的准确性。现有的基于可变观测器可变状态方程的状态观测大多采用“状态识别-状态确定-状态观测”的研究思路，这种先识别再观测的模式的计算时间往往较长，且状态观测的精度取决于状态识别的精度，因此，如何在降低模型运算量的情况下提高状态观测的精度成为研究的热点。

路面等级的准确识别对于道路的养护及管理、汽车悬架的智能控制、车队悬架的控制有重要影响。现代对于路面等级的识别分为接触式测量［13-15］、非接触式测量［16-18］和基于悬架响应的识别［19-24］。其中，基于悬架响应的识别成本低、实时性好，应用前景广泛，这种技术依赖于悬架的状态观测，分为智能识别［19-22］和统计识别［23-24］。智能识别是指通过状态观测获取轮胎的运动学特性，通过ANFIS［19-20］、神经网络［21-22］等智能算法完成对道路等级的规划，这种方法识别速度快，使用少量的样本量即可进行等级划分，但前期模型训练计算量较大［21］；统计识别是指通过状态观测提取完整的轮胎振动信息，通过分析、归纳进行道路等级识别，这种方法精度高，但对数据采样规模要求较高［23］。

本文首先基于LQR 算法与模糊控制算法，搭建路面自适应主动悬架系统，建立基于IMMKF 算法的路面自适应主动悬架系统状态观测器，通过系统仿真在变化等级的路面上进行路面自适应主动悬架系统的状态观测及路面等级识别，并通过IMMKF 观测器完成悬架的控制。

1 路面自适应主动悬架系统建模

结合模糊控制与LQG 控制，基于车身振动响应，建立一种基于舒适性的路面自适应主动悬架系统，使汽车在各种等级路面上行驶时的舒适性达到最优。

1.1 路面不平度建模

国际标准ISO8608：2016 将路面的功率谱密度Gq(n)作为路面不平度等级的分类标准，Gq(n)的拟合表达式为

式中：n0为参考空间频率；n为道路路面的空间频率；W为频率指数；Gq(n0)为参考空间频率对应的路面功率谱密度。一般n0=0.1 m-1，W=2，Gq(n0)通过查表获取。

路面的等级划分依赖于Gq(n0)的选取，国际标准ISO8608：2016 明确规定了各等级路面不平度系数的上/下限值，本文采用谐波叠加法生成空间域路面不平度模型，作为仿真系统的输入，谐波叠加法路面模型如下：

式中：l是道路纵向长度；Δni是频率区间；Gq(nm，i)是区间中心的谱密度；θi是[0，2π]内的随机变量，各θi相互独立。

参考式（2），设置总仿真时间为200 s，每隔0.25 s 采样一次，为验证模型状态观测精度及路面识别精度，生成A-B-D-C 级路面不平度模型，作为后续模型的输入模型，如图1所示。

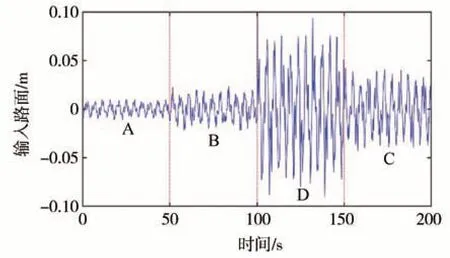
图1 路面输入

1.2 LQR主动悬架系统模型

建立1/4车辆主动悬架模型如图2所示。

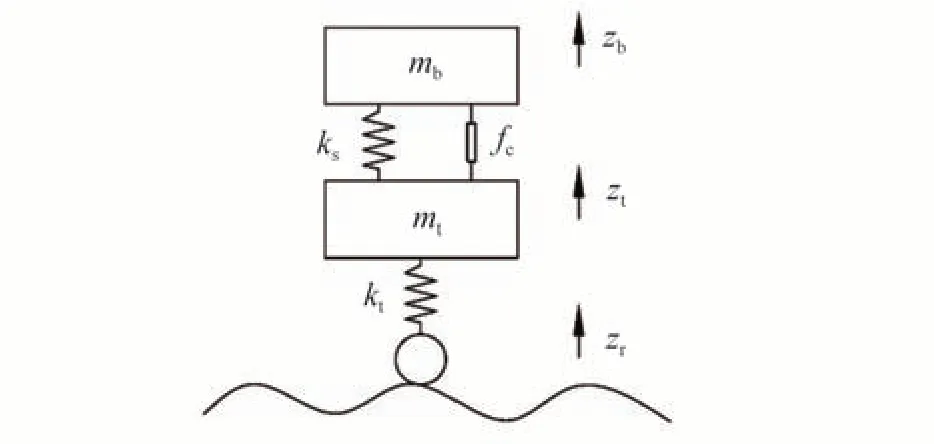
图2 1/4车辆模型

图中，mb是簧上质量，mt是簧下质量，ks是悬架刚度，kt是轮胎刚度，zb是簧上质量的位移，zt是簧下质量的位移，zr是路面输入，fc是可控阻尼力。

根据力学原理，有

将式（3）推广得到的系统状态方程为

其中

LQR主动悬架模型的状态向量和观测向量为

为合理控制车辆行驶时的平顺性与操纵稳定性，提升悬架性能，采用LQR 算法，计算最合适的可控阻尼力。构建LQR算法的目标函数为

其中：

式中：q1是悬架动挠度控制系数；q2是车身加速度控制系数；q3是轮胎动行程控制系数。通过合理赋值q1、q2、q3即可提升汽车在特定路面输入下的性能。

最优可控阻尼力通过式（6）计算。

式中P为Riccati方程的解［8］，即

求解出最优可控阻尼力后，LQR 主动悬架系统的状态方程为

其中：

悬架模型参数如表1所示。

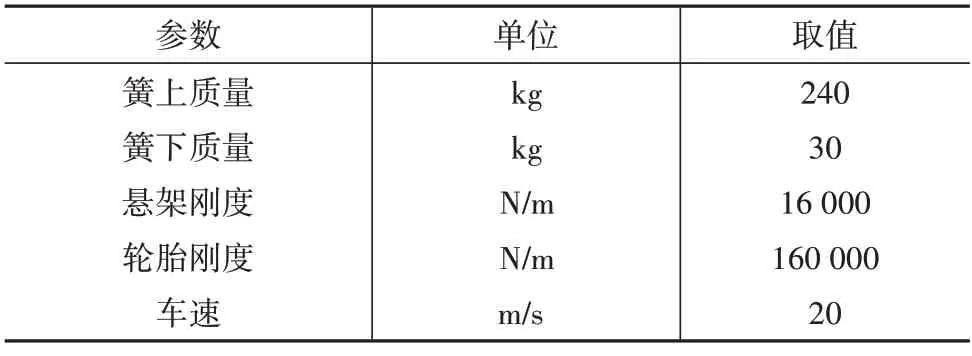
表1 悬架模型参数

为使悬架在不同路面上行驶时可根据车辆自身的振动响应合理地控制悬架系统参数，达到路面自适应控制的目的，首先采用NSGA-II 算法对建立的悬架在特定行驶路面的控制参数进行优化，作为后面模糊控制算法的初选值。

由于q3对悬架行驶特性影响较小，文本设置q3=0.0001，优化变量选择q1与q2，以悬架在某一等级路面下行驶时的车身加速度的均方根值(RMS)与悬架动挠度的最大值zb-zt(MAX)为优化变量，优化变量以取值最小为优化目标，即

NSGA-II 的种群数量设置为30，迭代次数设置为100，q1的优化范围为[0，109]，q2的优化范围为[0，2000]。

A级路面（Gq(n0)=16×10-6m3），车速为20 m/s下的优化结果如图3所示。

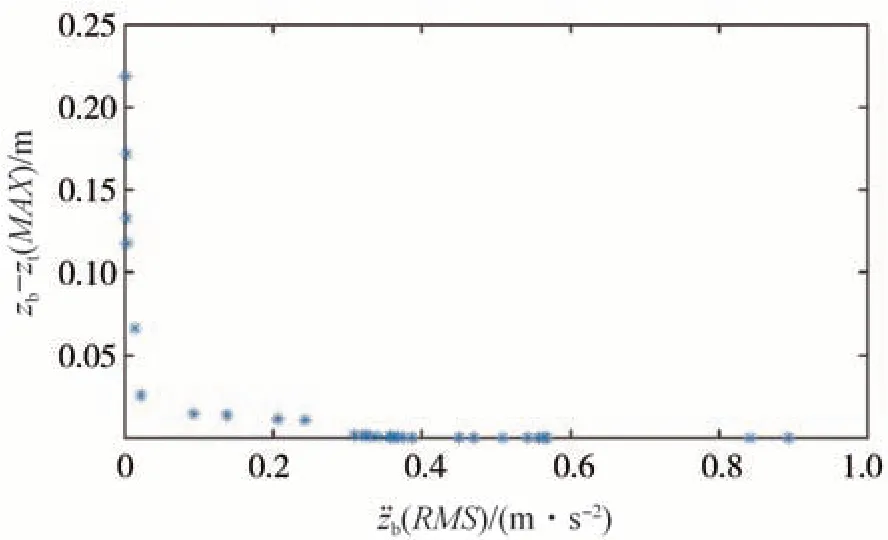
图3 A级路面NSGA-II优化结果

根据优化结果，手动选取最优控制参数作为LQR算法的控制参数的初选值，选取原则为

A、B、C、D级路面的优化结果如表2所示。

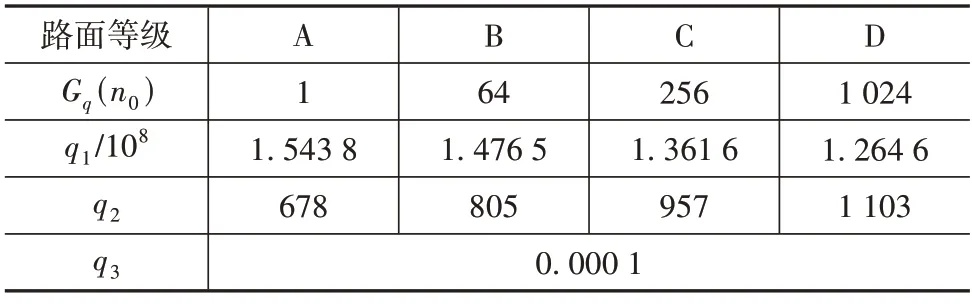
表2 各级路面LQR控制参数初选值

由表2 可知，以图1 所示的A-B-D-C 级路面模型为悬架输入时，控制参数q1的变化范围为[1.2646，1.5438]×108，q2的变化范围为[678，1103]。

1.3 基于模糊控制的路面自适应主动悬架

利用NSGA-II 的优化结果，建立模糊控制（fuzzy control）模型，根据车身的动态响应实现悬架的路面自适应控制。

本文设计的路面自适应主动悬架系统以舒适性为目标，使悬架动挠度的最大值zb-zt(MAX)不超过变形最大限制（15 cm）时的车身加速度最低。设计模糊控制模型时采用如下思路：当车辆由低等级路面（如B 级）行驶至高等级路面（如D 级）时，车身加速度的绝对值|变大，车身舒适性变差，为保证平顺性，对于LQG 算法，须降低q1、提高q2，使悬架动挠度的绝对值|zb-zt|变大，并降低车身加速度的绝对值相反，则提高q1、降低q2。据此设计的模糊输入隶属度函数如图4～图6所示。

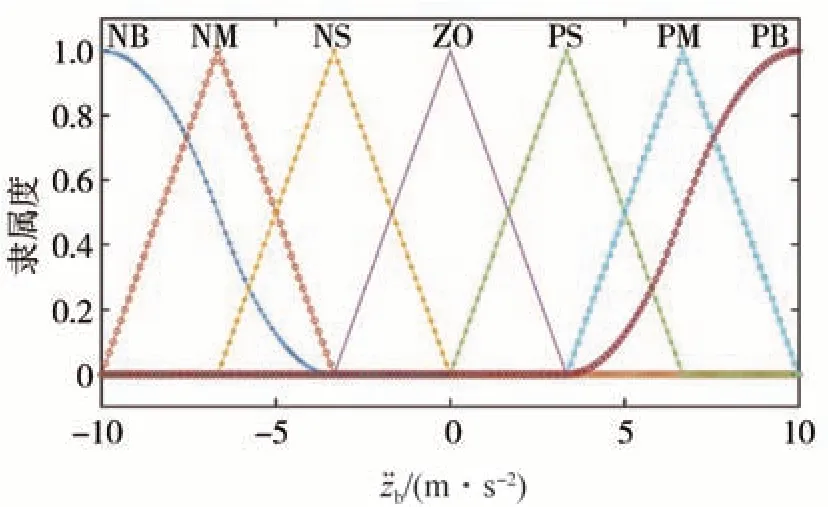
图4 车身加速度隶属度函数

图5 q1隶属度函数

图6 q2隶属度函数

模糊控制的输入与输出之间应用Centroid 方法（面积质心法），设计的模糊控制模型的输入量与输出量q1、q2之间的关系如图7和图8所示。

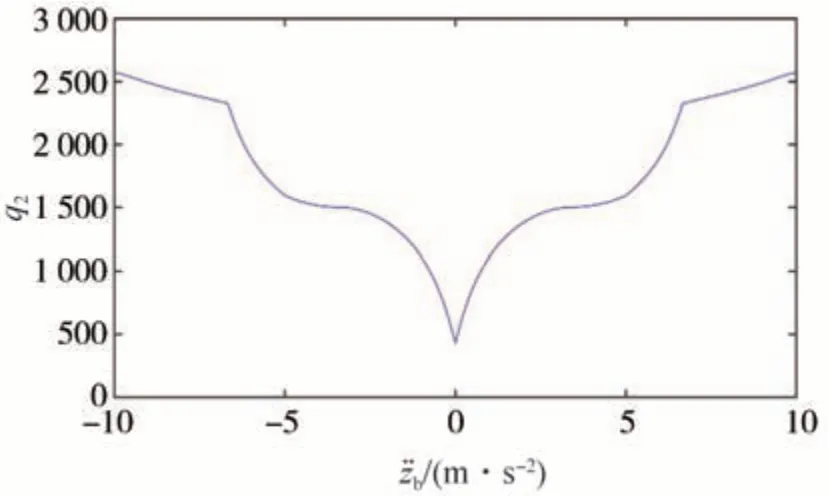
图8 与q2的关系图

将图1 所示A-B-D-C 级路面作为悬架输入，在图1 所示A-B-D-C 级路面上所建立的路面自适应主动悬架在各段路面下的输出结果如图9～图11所示。

图9 悬架响应-车身加速度

图10 悬架响应-悬架动挠度

图11 悬架响应-轮胎动变形

路面自适应主动悬架在各段路面下的输出结果数据如表3所示。

表3 路面自适应主动悬架输出结果

由表3 可见，该控制过程中，悬架动挠度zb-zt的最大值没有超过±15 cm，符合设计要求，且车身加速度的均方根值在各级道路上均较小。

该控制过程中的LQG 算法的控制参数q1与q2随时间的变化图像如图12和图13所示。

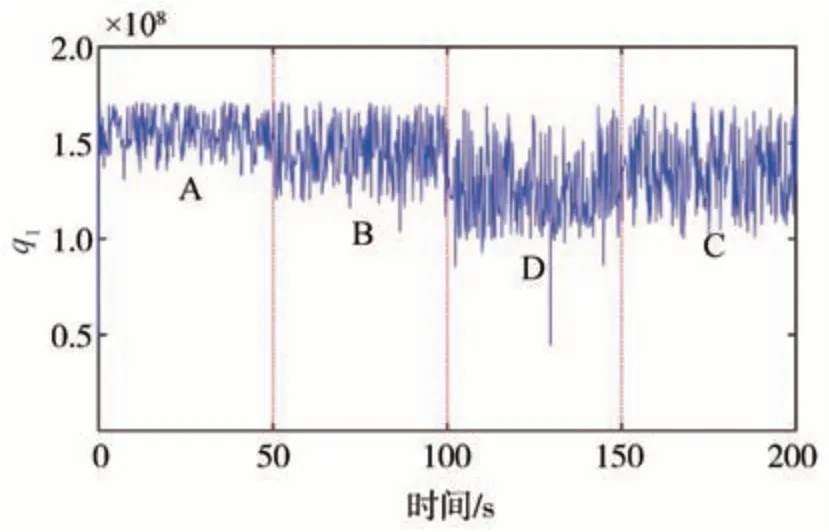
图12 q1结果

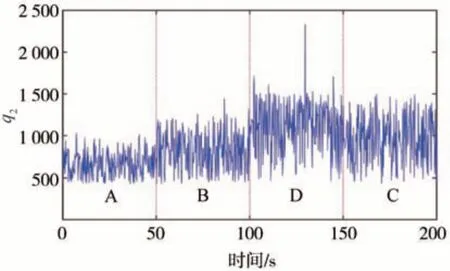
图13 q2结果

由图12和图13可知，所建立的路面自适应主动悬架可以根据悬架自身振动情况自动调整LQG 控制参数，保证汽车的舒适性，且随着路面等级的改变，q1、q2均围绕一个特定结果上下波动，计算各级路面下的q1、q2的平均值，作为后续IMMKF 路面自适应主动悬架状态观测器的子模型（状态识别矩阵），如附表1所示。

附表1 各级路面下的控制参数的平均值及QRV

2 基于IMMKF的主动悬架状态估计

主动悬架控制的过程中，各状态变量的跟踪及观测影响着悬架控制的精度与效果。现代在悬架控制领域多采用卡尔曼滤波器（Kalman filter，KF）进行悬架的状态跟踪，然而普通的卡尔曼滤波对系统模型的准确度要求较高，由于变化路面的参数不确定性，并且路面自适应主动悬架的状态参数随着路面等级与自身振动响应的改变而改变，采用普通的卡尔曼滤波器难以满足复杂多变的行驶条件下的路面自适应主动悬架的状态估计工作。

由于汽车在各等级路面下行驶时的最佳状态是可以预设的（即悬架系统在各等级路面下的典型行驶状态是已知的），对各等级路面进一步细分，建立对应路面下悬架状态观测子模型，各子模型组合的IMMKF 观测器可以在悬架动态控制下提高数据的观测精度，其模型概率计算结果也可用于道路等级的识别工作。

2.1 IMMKF主动悬架状态估计理论

根据式（8），实际运行状态下路面自适应主动悬架系统的状态方程的离散化形式为

式中：k为采样时刻；ω(k)为过程噪声；ν(k)为采样噪声；ω(k)与ν(k)近似为均值为0的高斯序列，时间间隔为0.25 s。

本文建立的IMMKF 主动悬架状态估计理论以各级路面的典型行驶状态（最佳LQG 控制状态）为子模型，具体步骤如下。

第1步：模型交互

第2步：卡尔曼滤波

状态预测方程为

先验误差协方差方程为

式中：Ai与Bi为模型i的状态方程；Qi为模型噪声。

再通过计算卡尔曼增益完成后验估计并更新误差协方差。

卡尔曼增益方程为

式中：H为系统的观测矩阵；R为观测噪声。

后验估计方程为

式中Zk为k时刻的观测值。

更新误差协方差计算方程：

第3步：更新模型概率

采用极大似然估计实现模型更新，通过计算当前模型和当前目标状态的相似度来给出当前最合适的跟踪模型所占权重在k时刻下模型i的最匹配的极大似然函数：

其中：

模型i的更新概率为

其中：

第4步：融合模型数据

融合计算得到的卡尔曼滤波后验估计值、更新误差协方差值、更新概率值，得到总体估计值与总体协方差值。

总体估计值为

总体协方差为

以上步骤相互迭代即可完成路面自适应主动悬架的观测。

2.2 IMMKF自适应悬架状态观测器的转移概率

由于建立的IMMKF 以各级路面最优LQG 控制模型为子模型，因此参考各级路面的转换，以正态分布为基础，设计IMMKF模型转移概率计算式。

设d为路面等级指数，满足：

对于路面等级指数为di的路面，基于式（27），设其模型转换概率服从N(di，1)，由正态分布可知，若d～N(di，1)，则

对式（28）进行改造，使模型i保持自身的概率占主导地位，构造IMMKF模型转换概率：

式中pdid是由路面等级指数为di的路面转移到d的路面的转移概率。以A 级路面为例，dA=4，其转换概率如图14所示。

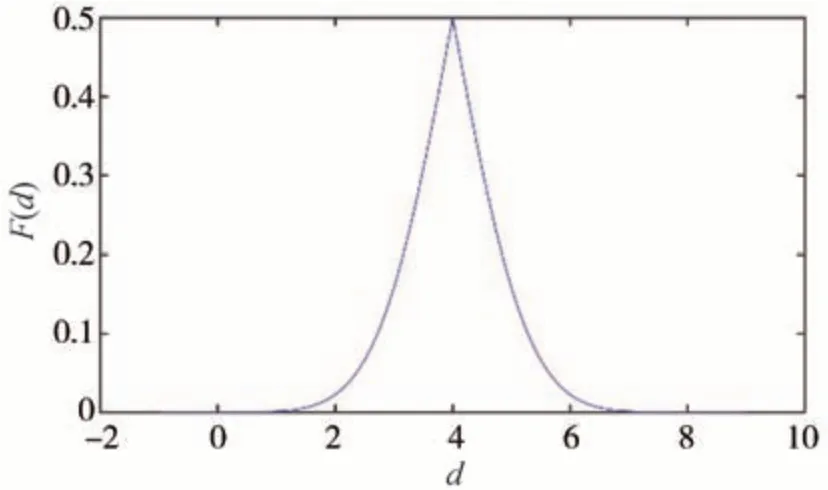
图14 A级路面转换概率图

为了使各转换概率的和为1，需要对各级路面下的转移概率进行加权平均，即

以附表1 中编号为A、B、C、D 的数据构造4 个子模型的IMMKF 观测器为例，各子模型之间的转移概率为

2.3 IMMKF自适应悬架状态观测器的Q与R

过程噪声协方差矩阵Q用于度量状态转移过程产生的噪声大小，其计算公式为

式中QRV用于度量道路输入速度值（高程值随时间的导数）的噪声大小，通过式（32）近似统计得到。

各级道路的QRV值如附表1所示。

量测噪声协方差矩阵R用于度量观测过程中产生的噪声大小。R的大小取决于IMMKF 的观测向量的选取，若选取车身加速度为观测向量，由式（4）、式（8）和式（11）可知，车身加速度的值随状态方程的改变而改变，由于建立的路面自适应主动悬架的状态方程理论上是随路面实时改变的，因此若选取车身加速度为观测向量，计算R时还需统计系统状态，因此选取为IMMKF 模型的观测量，观测向量为

量测噪声协方差矩阵R很大程度上取决于传感器的精度，为简化模型，参照文献［11］，将各级路面的R的统计平均值作为IMMKF 自适应悬架状态观测器的R的取值，设各子模型的R=0.012。

2.4 3种IMMKF自适应悬架观测器模型

所建立的自适应悬架模型，当输入模型的路面等级改变时，其状态也随之改变，即其状态对应于输入的路面等级。对于IMMKF 算法，其包含的子模型越精细，得到的观测结果越理想。下面以图1 所示的行驶工况为例，分别构造3 种IMMKF 观测器，每种观测器包含的子模型依次增多，用于对比、分析观测器的性能。

（1）4模型IMMKF观测器

参考附表1，选取编号为A、B、C、D的数据构造4个子模型构成IMMKF 观测器（IMMKF4）。4 模型IMMKF 观测器直接选取4 个标准路面下的LQG 控制模型作为状态观测器，具有一定的状态观测精度，并可用于道路分类识别。

（2）7模型IMMKF观测器

参考附表1，选取编号为A、Aab、B、Bbc、C、Ccd、D的数据构造7 个子模型构成IMMKF 观测器（IMMKF7）。7 模型IMMKF 观测器由于采用更多的模型，其状态观测精度较高，但由于采用Aab等跨等级路面模型，其道路识别精度较低。

（3）14模型IMMKF观测器

参考附表1，选取编号为A0、A1、A、A2、B1、B、B2、C1、C、C2、D1、D、D2、E1的数据构造14 个子模型构成IMMKF 观测器（IMMKF14）。14 模型IMMKF 观测器采用子模型最多，其观测精度也最高，且不存在跨等级路面模型，其道路识别精度也最高。

分别采用A 级、C 级路面下最优LQG 矩阵（附表1 中编号A、C 的数据）为观测器构造普通卡尔曼滤波器（KFA、KFC），通过与构造的3 个IMMKF 观测器的仿真对比验证IMMKF观测器的精度。

2.5 仿真分析

利用Matlab软件完成3种IMMKF状态观测器及A 级KF 观测器、C 级KF 观测器的仿真，状态估计误差的平均值对比如表4所示。

表4 各级路面仿真结果误差对比 %

由表4 结果可知，各级路面下3 种IMMKF 观测器的观测结果均优于普通卡尔曼滤波KF，验证了IMMKF 的优越性。3 种IMMKF 观测器中，14 模型IMMKF 观测器的观测精度最高，7 模型IMMKF 观测器次之，4模型IMMKF观测器精度最差。其原因是，由于悬架的状态方程随输入路面等级的变化而不断改变，采用越精细的观测模型进行状态观测，观测方程越接近于真实的状态方程，其观测精度越高。

滤波结果中，zb-zt与zt-zr的误差较大，其余项误差均较小，对于IMMKF14 而言，相比于KFA，其zb-zt误差最大降低了83.93%误差最大降低了98.17%，zt-zr误差最大降低了59.92%误差最大降低了95.86%，验证了IMMKF观测器的优越性。

本文所建立的IMMKF14 状态观测器与文献［11］中的UKF、AUKF仿真结果对比如表5所示。

表5 仿真结果误差对比 %

由表5 可见，相对于AUKF 与UKF，IMMKF14 的精度最高。从算法复杂度的角度看，IMMKF 与AUKF 均为平方阶，从整体上看，相对于“状态识别-状态确定-状态观测”的观测模式，本文建立的IMMKF 模型简化了观测流程，避免了“状态识别-状态确定”的过程，在一定程度上降低了模型的计算成本。

仿真过程中各观测量如图15～图18所示。

图15 zb-zt结果误差

图16 结果误差

图17 zt-zr结果误差

图18 结果误差

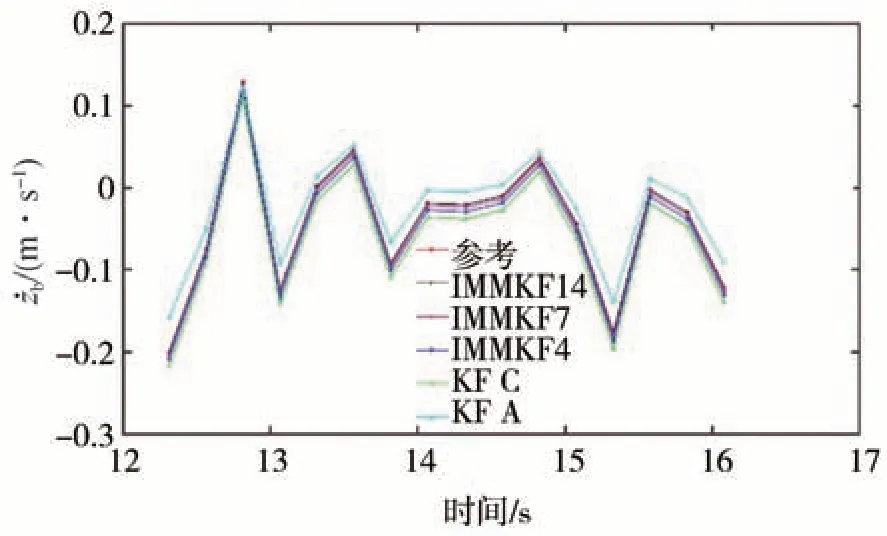
图19 结果误差（部分）

由图15～图19 可知，3 种IMMKF 观测器的精度高于两个普通KF 观测器，验证了IMMKF 观测器的优越性。

仿真过程中的IMMKF14 的混合概率随时间变化过程如图20所示。

图20 IMMKF14观测器的混合概率

由图20 可知，在IMMKF14 跟踪仿真的过程中，由于路面等级的变化，悬架的车身加速度发生改变，经路面自适应主动悬架的控制，最终导致模型混合概率的识别呈现出A-B-D-C 级路面变化的趋势，对于一次采样过程，理论上可出现4 种混合概率结果，其中最大的混合概率对应的子模型即可认为是当前发生的模型，即悬架采用的控制模型，也是悬架输入的道路模型，可用于路面自适应悬架对路面等级的识别工作。

对于图20而言，每一个采样步内均含有14个模型的概率。统计图20 中每一个采样步内概率最大的模型的编号，将A0、A1、A、A2划分为A 级路面，将B1、B、B2 划分为B 级路面，将C1、C、C2 划分为C 级路面，将D1、D、D2 划分为D 级路面，得到的道路识别结果如图21所示。

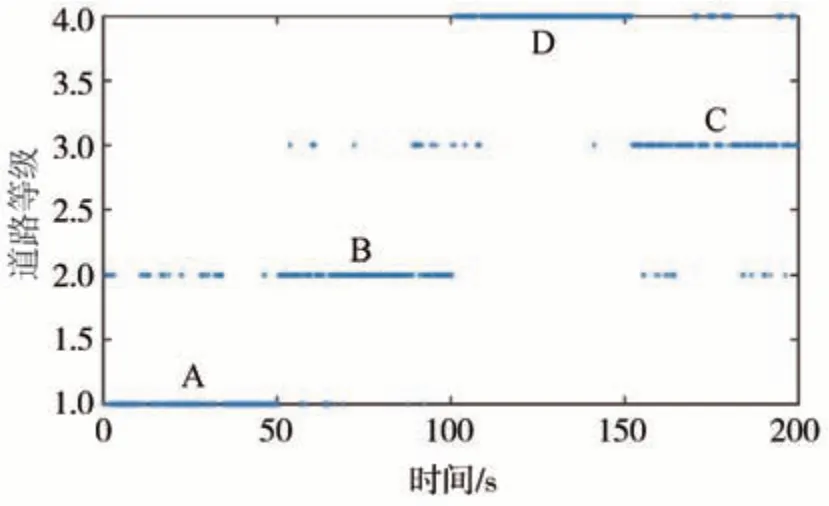
图21 采样步为1时的路面等级识别结果

由图21 及路面特性可知，各等级路面可能杂糅其他等级路面（如A 级路面可能含有B 级路面的成分），影响了IMMKF 状态观测器对模型概率的计算，造成了路面等级识别的误差。下面以3 种IMMKF观测器的仿真结果为例，每隔n个采样步统计采样步内混合概率最大值的众数，作为路面等级的识别结果，其识别正确率如表6所示。

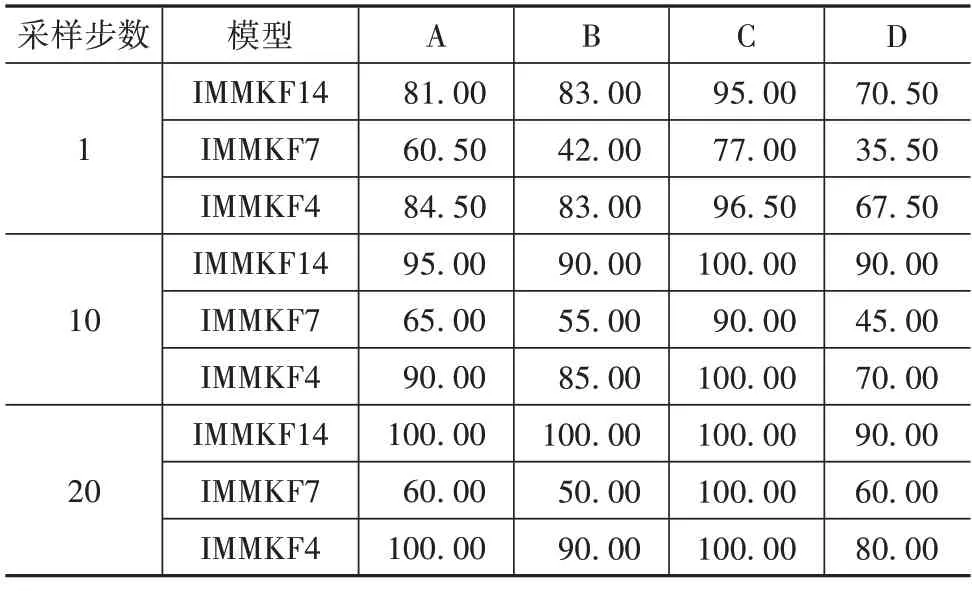
表6 路面等级识别正确率 %

由表6 可见，当路面等级统计采样步逐渐变大时，采样精度逐渐变大。3 种模型中，IMMKF14的路面识别正确率最大，IMMKF7 因存在跨路面等级子模型导致其识别精度最低。

3 种IMMKF 观测器中，IMMKF14 具有最高的状态观测精度与路面识别正确率，认为是最优观测器。

3 基于IMMKF的主动悬架控制

将建立的IMMKF14 状态观测器用于路面自适应主动悬架控制，将IMMKF14的滤波值作为路面自适应主动悬架系统的状态值，其控制流程如图22所示。

图22 基于IMMKF的自适应主动控制悬架控制流程图

将图1 所示路况信息作为系统输入，依次进行基于IMMKF14的自适应主动悬架模型、普通LQG主动悬架模型、被动悬架模型的仿真，其中，普通LQG主动悬架模型选取表4 所示C 级路面最优控制参数构建状态方程，被动悬架模型的阻尼设置为980 N/（m/s）。利用Matlab 软件进行仿真，各级路面下的输出量的仿真结果的均方根值对比如表7所示。

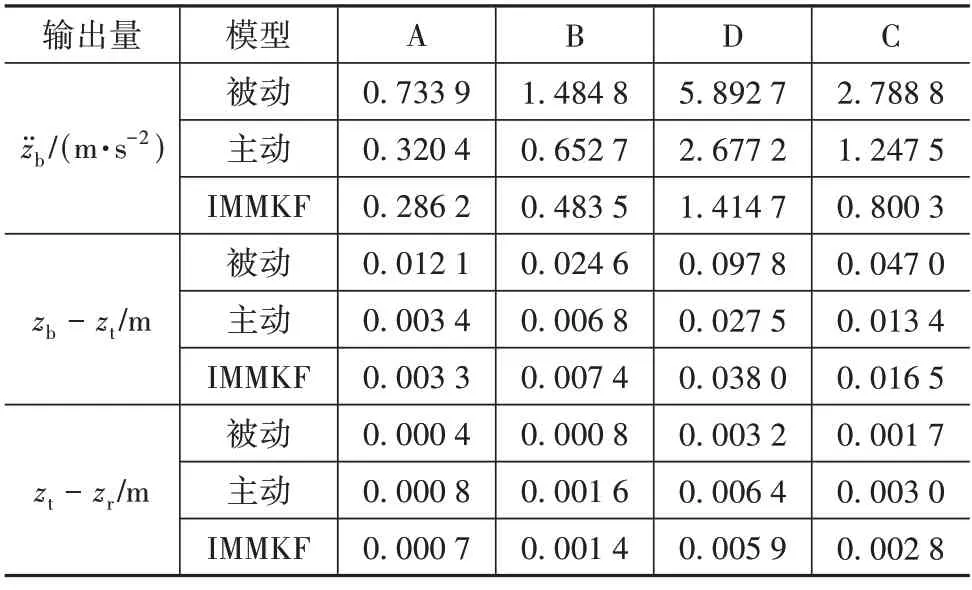
表7 各级路面仿真结果对比

仿真结果如图23～图25所示。

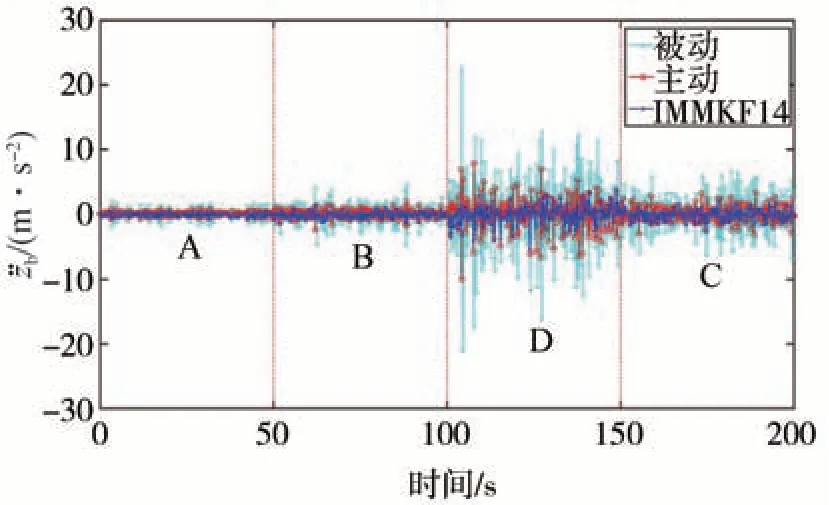
图23 车身加速度仿真结果图

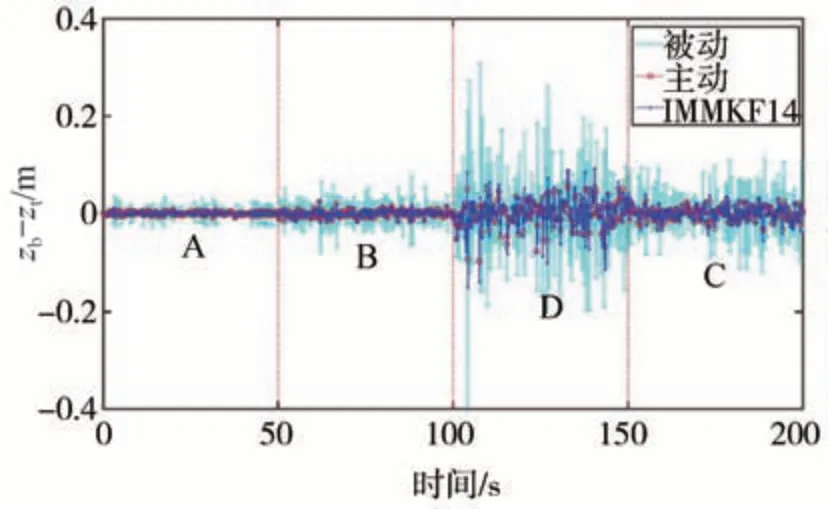
图24 悬架动挠度仿真结果图

图25 轮胎动行程仿真结果图

由表7、图23～图25 的仿真结果可知，相对于被动悬架，建立的基于IMMKF14的路面自适应主动悬架模型的车身加速度与悬架动挠度zb-zt均较小，其中车身加速度相对于被动悬架最大降低了75.99%、悬架动挠度zb-zt最大降低了72.73%，而IMMKF14 的轮胎动行程zt-zr虽较被动悬架大，但在数值上仍保持在一个很低的水平；相对于LQG 主动悬架，建立的基于IMMKF 的路面自适应主动悬架模型的车身加速度较小，最大降低了47.16%，悬架动挠度zb-zt与轮胎动行程zt-zr则略大于LQG主动悬架，但在数值上仅有微弱区别。说明建立的基于IMMKF14 的路面自适应主动悬架模型在变化路面条件下可以有效降低车身加速度，提升车辆的舒适性。

4 结论

本文结合路面功率谱密度与谐波叠加法，生成A-B-D-C 级空间域路面不平度模型，作为仿真系统的输入。建立了LQG 主动控制悬架模型，通过NSGA-II 算法完成各级路面下最优控制参数q1、q2的初选。再通过模糊控制算法，以车身加速度值为输入，LQG 控制参数q1、q2为输出，建立一种基于舒适性的路面自适应主动悬架系统，仿真结果表明，该系统可根据路面高程值的变化自动调整悬架状态参数。

基于IMMKF算法，以各等级路面下最优LQG模型为子模型，建立了3 种IMMKF 悬架状态观测器，用于路面自适应主动悬架系统的状态观测，3 种IMMKF观测器中，IMMKF14的性能最好。通过与普通卡尔曼滤波观测器的仿真对比，结果表明IMMKF悬架状态观测器可有效提升状态观测精度，并可用于路面等级识别。

结合路面自适应主动悬架系统与IMMKF14 悬架状态观测器，建立了基于IMMKF 的自适应主动悬架控制器，通过与被动悬架、普通LQG 主动悬架的仿真对比，结果表明，在等级变化的路面上，基于IMMKF 的自适应主动悬架控制器可有效降低车身加速度、提升汽车的乘坐舒适性。