考虑环空液体热力学特征的持续环空带压预测模型研究
2023-07-31丁亮亮代先涛李帅张强
丁亮亮,代先涛,李帅,张强
(1.西南石油大学机电工程学院,成都 610500;2.中石化西北油田采油一厂,巴音郭楞蒙古自治州 841602)
近年来,持续环空带压已成为气井普遍存在问题,特别是塔里木油田及西南油气田气井持续环空带压问题尤为严重[1-3]。持续环空带压是指井口环空压力泄放后短时间内又恢复到泄压前水平的现象[4]。油管、套管及水泥环等井生产安全屏障组件密封失效是其产生的主要原因[5-6]。持续环空带压不仅增加了气井管理难度、降低气井采收率,严重时甚至会导致井口装置破损失效,造成巨大经济损失及安全事故[7-9]。
因此,急需开展气井持续环空带压特征及机理研究。针对气井环空带压问题的研究最早可追溯到20世纪80年代,外国学者最先研究了环空带压产生机理并提出了持续环空带压概念。学者们深知持续环空带压的产生影响因素多、危害大,因此从未停止过这方面的研究。张波等[10]为探究通过水泥返高调控持续环空压力的可行性,建立了基于物质守恒和体积守恒的含液环空持续环空压力计算模型。罗伟等[11]展开了油管多漏点泄漏规律及控制研究,将多漏点泄漏分为多种情况并利用现场实例验证了所提出漏点的合理性。李磊等[12]基于气体渗流方程,利用水泥环综合渗透率表征水泥环失效程度,建立了考虑气体溶解的持续环空压力预测模型。Zhang等[13]建立了由多油管泄漏点引起的持续环空压力模型并分析了泄漏率、环空持续压力与流体分布之间的耦合关系。练章华等[14]建立了油套环空带压预测模型,并利用模型对油管漏点当量直径进行了拟合。Kazemi等[15]提出了一种改进的环空带压测试方法,并指出漏压为0并不一定意味着泄漏很小,还取决于水泥顶部环空液柱的高度和性质。阎卫军等[16]为准确预测套管环空上方的持续环空压力,将环空窜流等效渗透率计算方法补充到持续环空压力预测模型。
以上学者针对气井持续环空带压的研究具有重要的参考价值及意义。但学者们在建模过程中均未考虑环空温压变化所引起的环空液体膨胀或收缩效应,并且学者们均将环空液体压缩系数视为定值,并未考虑温压耦合作用[17]下对环空液体热膨胀系数、压缩系数影响。然而这两个系数是预测环空压力基础性、关键性参数[18]。为此,考虑温压耦合作用对环空液体热力学性质影响,建立一种新的环空带压数学预测模型,以井筒温压场预测数据及A气井现场实测数据为基础,验证模型的准确性,利用模型对A气井进行了环空压力诊断及不同参数对环空压力、气柱高度的影响分析,为现场环空带压预测及管理提供理论支撑。
1 力学模型
油管气体在油管漏点内外壁压力差作用下泄漏至环空并在井口聚集,最终形成环空带压,如图1所示。在气体泄漏至环空过程中由于井筒传热会导致环空温度变化,影响环空液体热膨胀系数、压缩系数,最终影响环空压力预测准确性。
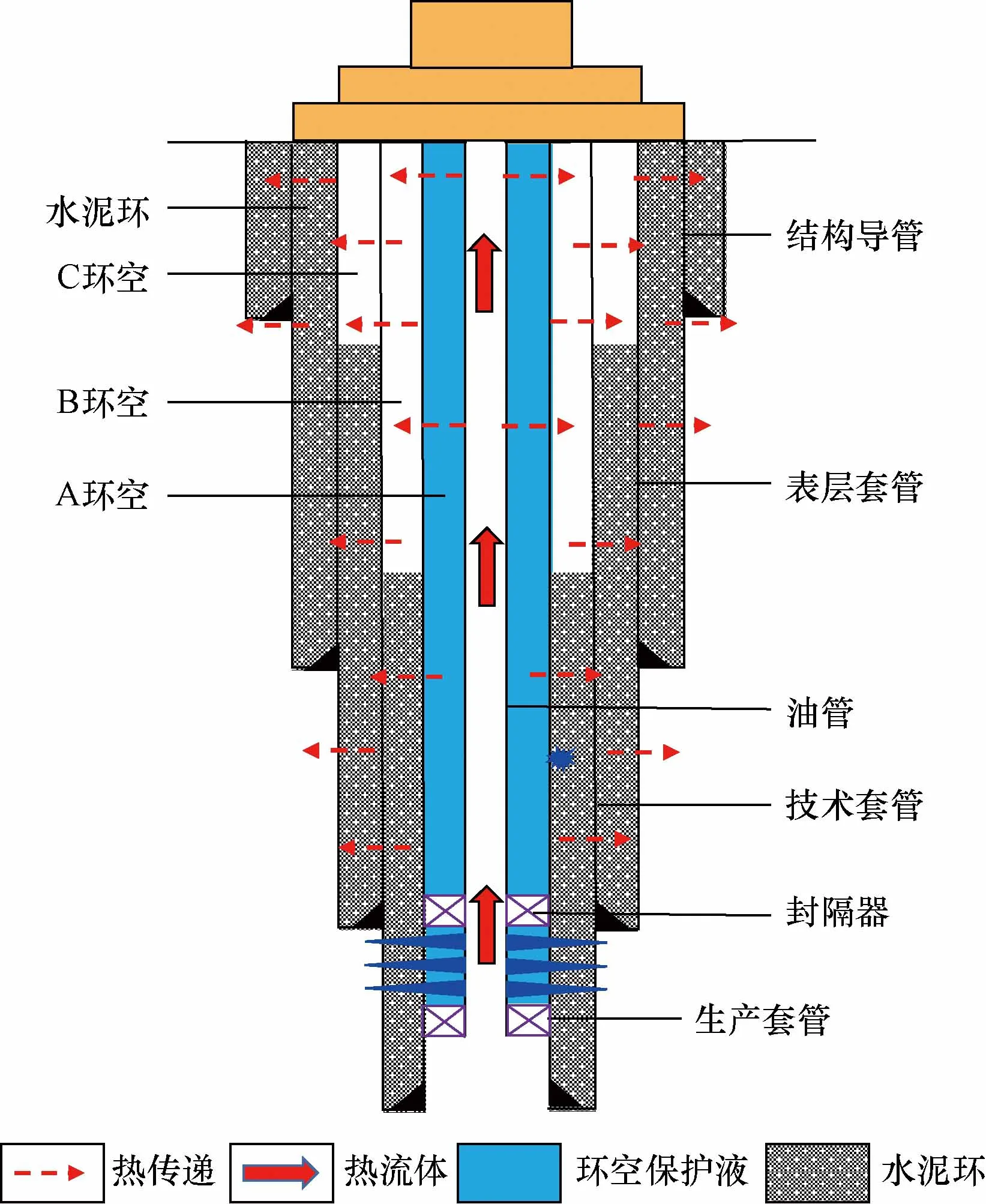
图1 气井结构示意图Fig.1 Gas well structure diagram
为此首先建立井筒温压场预测模型,利用井筒温压场预测模型预测油管内温度、压力及油套环空温度。随后充分考虑温压耦合作用对环空液体热力学参数影响,建立持续环空带压预测模型。最后,以井筒温压场预测数据为基础,结合现场数据验证所建模型准确性,利用模型对气井环空压力恢复过程进行诊断并分析不同参数对环空压力、气柱高度影响。
1.1 井筒温压场预测模型
气井测试过程中,井筒温度场变化遵循质量守恒、动量守恒、能量守恒方程及状态方程,井筒温度、压力可通过式(1)求得。
(1)
式(1)中:下标g、t、ti分别表示油管内流体、油管柱和油管内壁面;ρ为气体密度,kg/m3;v为气体流速,m/s;z为井深,m;t为时间,s;c为比热,J/(kg·K);hti为油管内壁对流换热系数,W/(m2·K);kg为气体热传导系数,W/(m·K);T为温度,K;d为管柱直径,m;f为壁面摩阻系数,无量纲;p为压力,MPa;γg为气体相对密度,无量纲;Zg为气体偏差因子,无量纲;rti为油管内径,m;0.016为天然气的摩尔质量,kg/mol;R为气体常数,R=8.314 Pa·m3/(mol·K)。
式(1)中摩阻系数f与流体流态相关,不同流态下气体摩阻系数可通过式(2)式求得[19]。
(2)
式(2)中:Re为雷诺数,无量纲。
雷诺数为判断流体流动状态的判据,可通过式(3)计算。
(3)
式(3)中:υ为运动黏度,m2/s。
不同井筒流体流动情况下壁面对流换热系数h与流体流速、流体密度、比热、黏度、导数系数等参数有关,对流系数可通过式(4)计算。
(4)
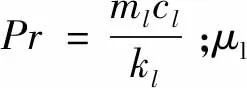
1.2 环空压力预测模型
1.2.1 气体泄漏流量计算
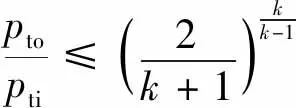
(5)
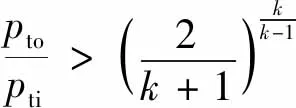
(6)
式中:Qc为标况下气体流量,m3/d;d1为漏点当量直径,mm;T1为油管漏点外壁温度,K;k为绝热指数,通常取1.28;pti、pto分别为油管漏点内、外壁压力,MPa。
1.2.2 油管漏点外壁压力计算
流体密度是温度及压力的函数,而环空轴向上不同位置处环空压力、温度并不相同,因此流体密度也不相同。为了更加精确求解油管外壁压力,将整个环空沿轴向划分为若干个网格,则油管外壁压力计算公式为
(7)
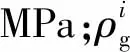
Ellis等[20]、Oudemanp[21]研究发现,环空液体物理性质与水的物理性质相似,因此借助文献[22]中温度为27、107、127 ℃,压力为1、10、100 MPa下水的密度数据,利用二元拉格朗日插值法拟合密度关于温度及压力多项式[22],如式(8)所示。
ρL=P(a1T3+a2T2+a3T+a4)+
P2(a5T3+a6T2+a7T+a8)+
a9T+a10T2+a11T3+1 002.01
(8)
式(8)中:ρL为水的密度,kg/m3;P为压力,MPa;T为温度,℃;a1=-2.057 61×10-8;a2=1.958 33×10-5;a3=-2.008 28×10-3;a4=4.944 26×10-1;a5=-2.338 20×10-11;a6=-3.598 48×10-8;a7=3.883 58×10-6;a8=-5.495 44×10-4;a9=-3.598 48×10-8;a10=3.883 58×10-6;a11=-5.495 44×10-4。
为验证拟合公式准确性,利用式(8)计算温度为177 ℃,压力为1、10、100 MPa下水的密度并与文献[22]中密度进行对比,对比结果如表1所示。可以看出,最大误差仅为0.16%。
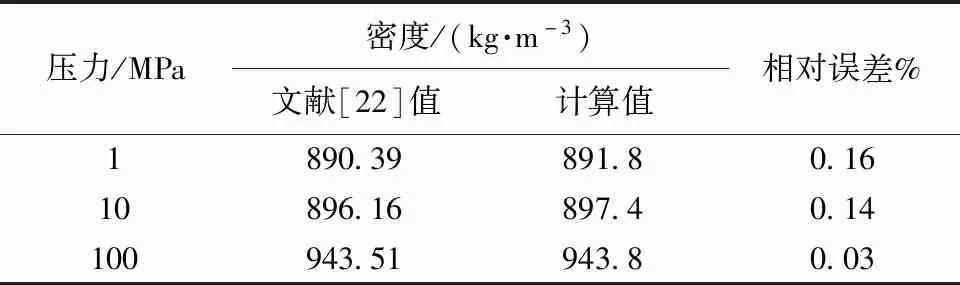
表1 公式计算的密度值与文献[22]对比Table 1 The equation calculates the density of water and compares it with the ref.[22] value
1.2.3 环空体积变化量及环空带压值计算
液体热膨胀性、压缩性是导致环空体积变化的主控因素。而液体热膨胀系数、压缩系数是密度分别与温度、压力的导函数,计算公式分别为
(9)
(10)
式中:CT为环空液体热膨胀系数,K-1;Cm为环空液体压缩系数,MPa;V为液体体积,m3;dV为液体体积变化量,m3;dT为液体温度变化量,K;dρ为液体密度变化量,kg/m3;dp为压力变化量,MPa。
将式(8)分别对温度、压力求导后代入式(9)、式(10)得到热膨胀系数、压缩系数计算公式分别为
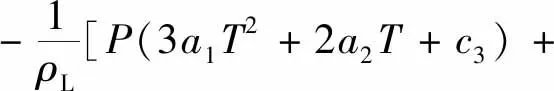
P2(3a5T2+2a6T+a7)+a9+
2a10T+3a11T2]
(11)
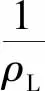
2P(a5T3+a6T2+a7T+a8)]
(12)
利用式(13)计算温度为7~175 ℃、压力为1~100 MPa下水的密度,求导后分别代入式(11)、式(12)求得热膨胀系数、压缩系数如图2所示。可以看出,水的热膨胀系数及压缩系数随温度及压力的增加而不断增大,且两者温度、压力由7 ℃、1 MPa增大至175 ℃、100 MPa后,热膨胀系数、压缩系数分别增大了7.16倍、2.07倍,由此可知温度、压力对热膨胀系数、压缩系数有较大的影响。因此,在计算环空液体体积变化时采用不同温度及压力下的热膨胀系数、压缩系数。
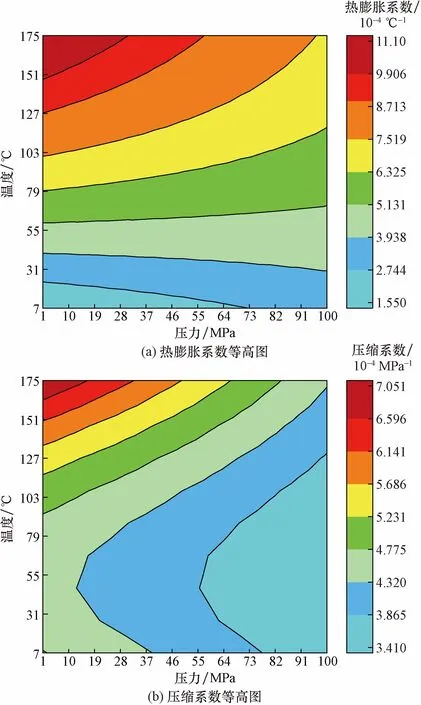
图2 水热力学参数随温压变化等高图Fig.2 Contour diagram of water thermodynamic parameters varying with temperature and pressure
气体泄漏至环空过程中,环空压力值与时间密切相关,将环空压力恢复周期分为若干个时间微元,时间步长为Δt,第x时间段内由于井筒温度变化而导致环空液体体积变化量可由式(13)计算。
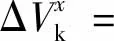
(13)
由于压力升高导致环空液体压缩总体积可由式(14)计算。
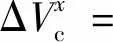
(14)
假设油管及套管为刚性材料,环空总体积保持不变,即环空内气体与液体体积变化量相等,规定使气体体积增大为正,环空气体体积变化量可由式(15)计算。
(15)
根据PVT方程,环空气柱满足式(16)。
(16)
(17)
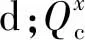
将式(13)、式(15)代入式(14)得到第x时刻环空压力计算公式为
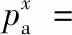
(18)
1.3 模型求解
井筒温压场预测及持续环空压力预测模型求解步骤如下。
步骤3重复步骤1、步骤2直至算至封隔器位置。
步骤5再次判断油管内外壁压力是否满足精度,若满足精度结束运算,否则执行步骤1、步骤2。
2 实例分析
2.1 基础参数
塔里木盆地克深气田高压气井-A井2016年10月4日投产,完井深度7 720 m,地温梯度2.35 ℃/100 m;随后油套环空压力随生产制度反复波动,最后2019年3月油套连通。其井身结构和流体相关参数如表2所示。
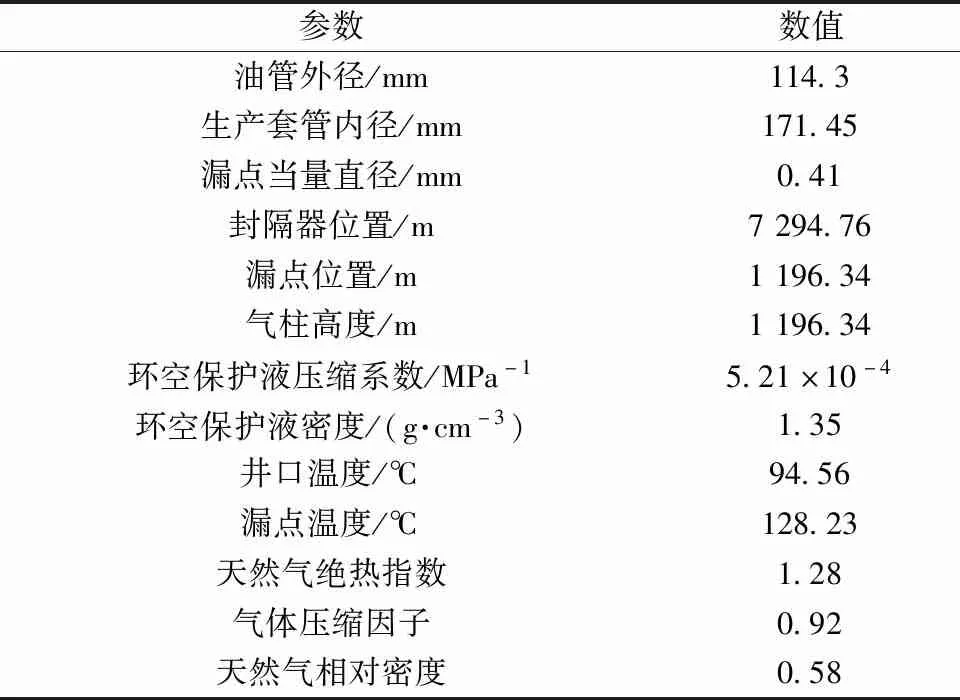
表2 A气井井深结构及流体相关参数Table 2 Well depth structure and fluid related parameters of a high temperature and high pressure gas well
2.2 环空压力预测模型对比分析
图3为环空压力实测数据与模型预测数据对比。可以看出,考虑温度压力对环空液体热膨胀系数、压缩系数影响所建立模型环空压力预测数据与实测数据相比平均精度高达96.05%,而未考虑温度压力对环空液体热膨胀系数、压缩系数的影响,模型平均精度为94.86%。即所建立的模型预测数据更具参考价值。
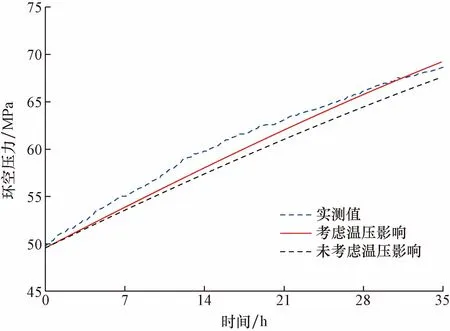
图3 实测数据与模型预测数据对比Fig.3 Comparison of measured data and model prediction data
2.3 环空压力恢复过程诊断分析
利用所建模型对A气井进行环空压力恢复过程模拟研究,环空压力及漏点流量随时间变化关系如图4所示。可以看出,A气井环空压力稳定至为82.22 MPa,环空压力从49.57 MPa恢复到稳定值需75 h。在环空压力恢复过程中油管漏点流量与时间呈抛物线关系,最大泄漏流量为1 931.23 m3/d。
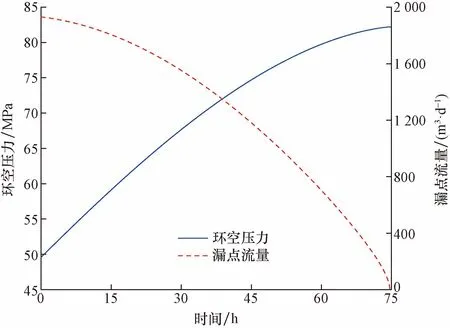
图4 环空压力及漏点流量随时间变化图Fig.4 Diagram of annulus pressure and leakage flow over time
图5为环空压力恢复过程中环空气柱高度随时间变化,可以看出,环空压力恢复至约50 h时气柱高度达到最大值1 215.87 m,随后下降至1 209.60 m,即该井气柱高度随时间延长呈先增大后减小趋势。
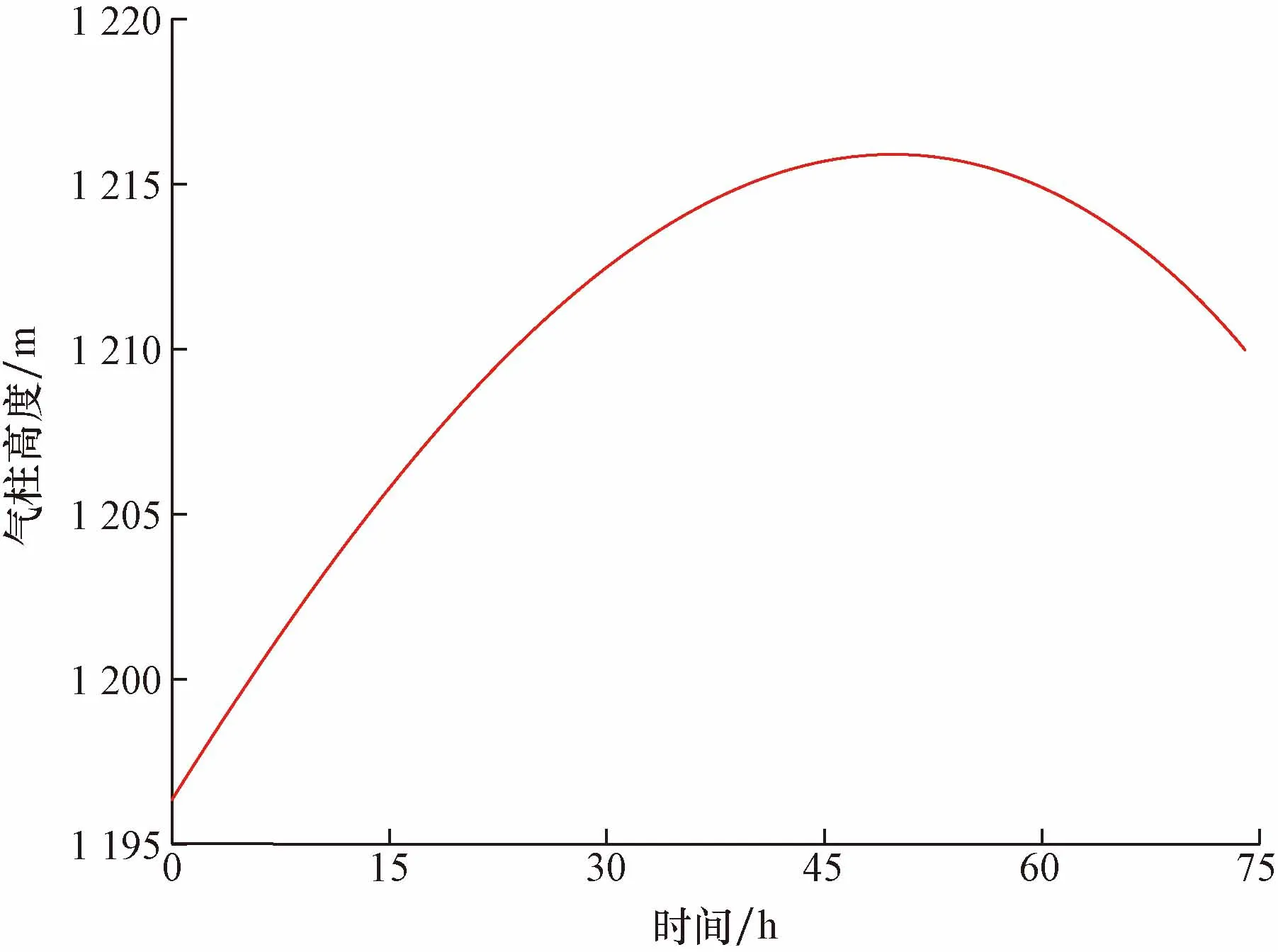
图5 环空压力恢复过程中环空气柱高度随时间变化图Fig.5 Diagram of the height of the ring air column changing with time during air pressure recovery
2.4 环空压力可调控因素敏感性分析
影响气井环空压力恢复过程及气柱高度变化的因素主要包括漏点大小、漏点位置、环空液体密度、气柱高度、环空压力及环空温度。其中漏点大小及漏点位置为不可控因素,而对于已油套联通的井环空液体密闭对环空压力值影响不大,因此主要研究初始环空气柱高度、压力及温度对环空压力恢复过程及气柱高度影响规律。
图6为初始气柱高度对环空压力恢复过程影响,可以看出,当气柱高度hg=596.34 m时,环空压力稳定值为76.04 MPa,而当hg=1 196.34 m时,环空压力稳定增大至82.22 MPa,增加了6.18 MPa。即随着环空气柱高度的增加,环空压力稳定值随之增大。但在环空压力未达到稳定值前,同一时刻气柱高度越低环空压力值越高,由此可知气柱高度越高环空压力恢复速度越快。因此应结合井实际情况预留一定环空气柱高度,有利于降低环空压力恢复速度。
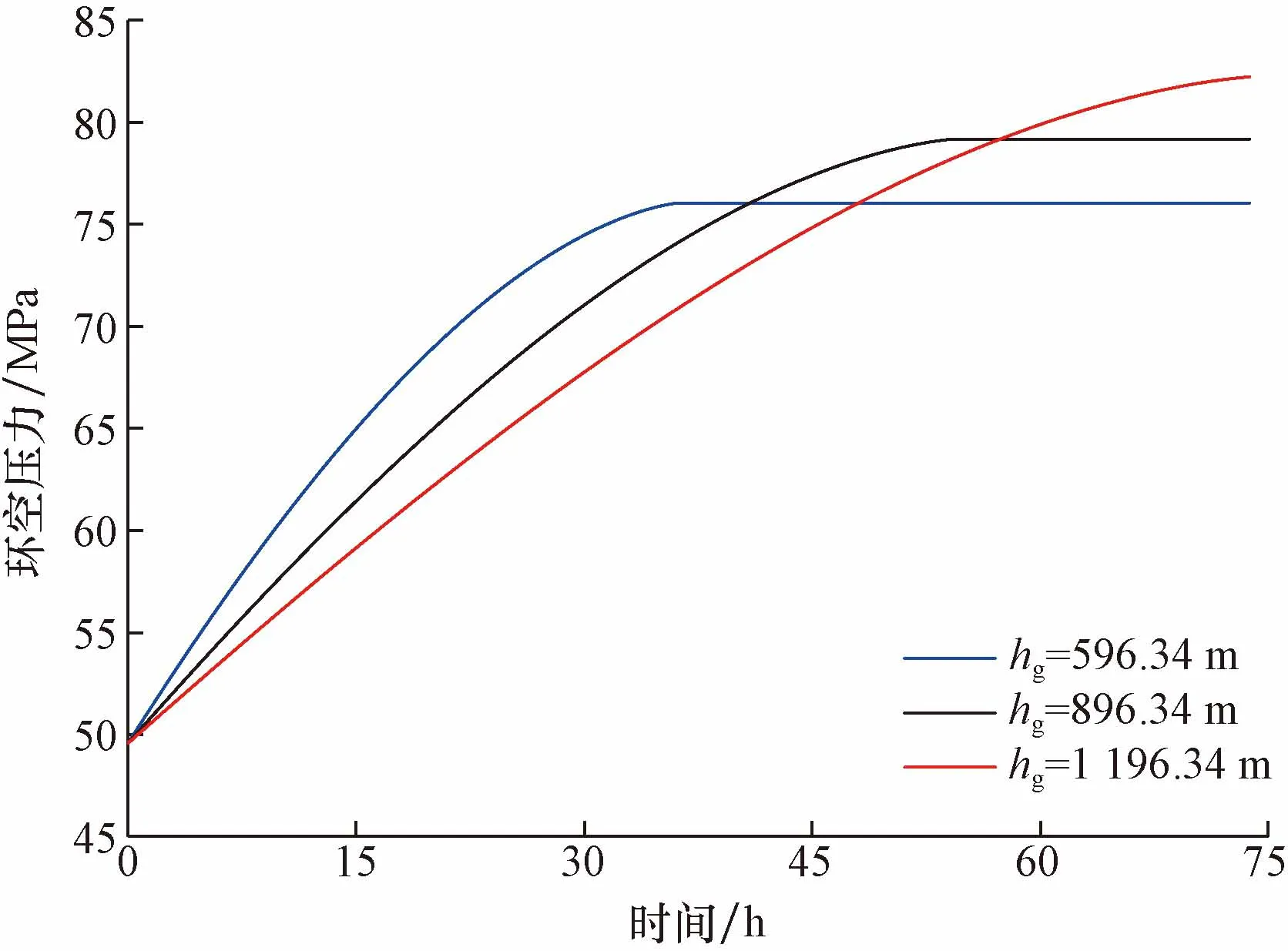
图6 初始气柱高度对环空压力恢复过程影响图Fig.6 Diagram of influence of initial column height on annular pressure recovery process
图7为环空压力恢复过程中气柱高度随时间变化。可以看出,初始气柱高度越低,环空压力恢复到稳定值后气柱高度变化越大。这是因为,气柱高度越低则环空液体体积越大,根据体积守恒原则,经过环空压力恢复过程后气柱高度变化越大。
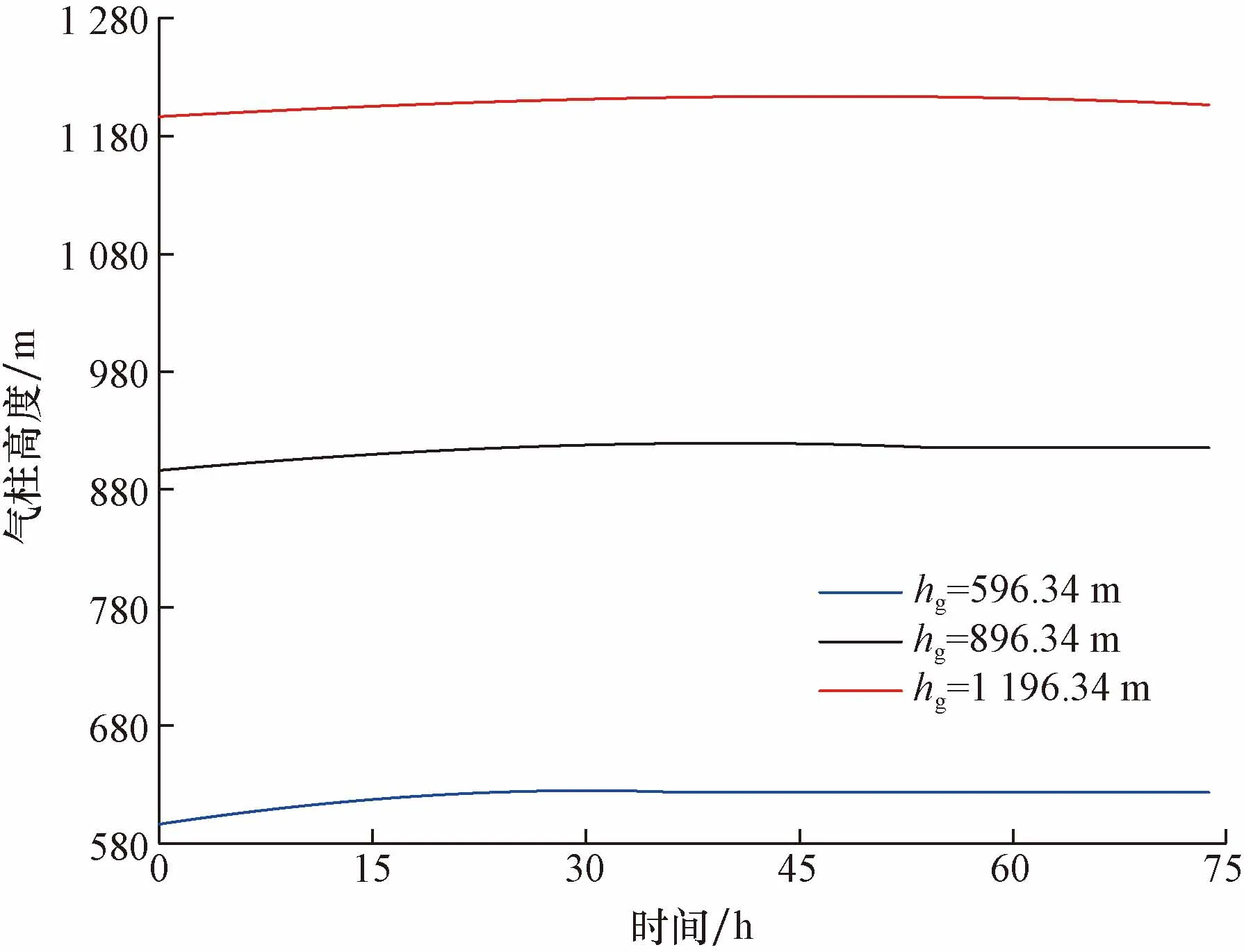
图7 环空压力恢复过程中气柱高度随时间变化图Fig.7 Diagram of column height variation with time during annulus pressure recovery
因为环空液体热膨胀系数、压缩系数是温度及压力的函数。井口环空温度不同将导致两个系数的不同。为此环空温度T分别取40、60、80 ℃,进行环空压力恢复过程模拟,模拟结果如图8所示。可以看出,环空温度对环空压力稳定值基本无影响,但对环空压力恢复速度有影响。同一时刻环空温度越低,环空压力值越低。因此建议在完井时使用传热效率低的管柱及环空液体,有利于降低环空压力恢复速度。
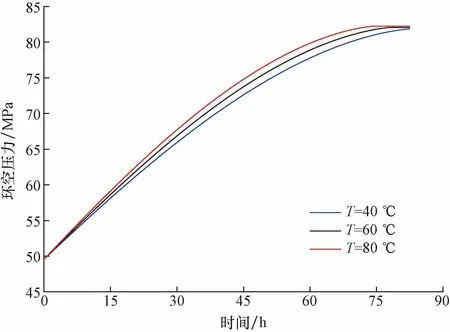
图8 初始环空温度对环空压力恢复过程影响Fig.8 Influence of initial annulus temperature on annulus pressure recovery process
图9为初始环空温度对环空压力恢复中气柱高度的影响。可以看出,当T=40 ℃时,经过环空压力恢复过程后,气柱高度由1 193.34 m变为1 203.59 m,当T=80 ℃时,气柱高度由1 193.34 m变为1 206.62 m。由此可知气柱高度变化量与环空温度呈正相关。
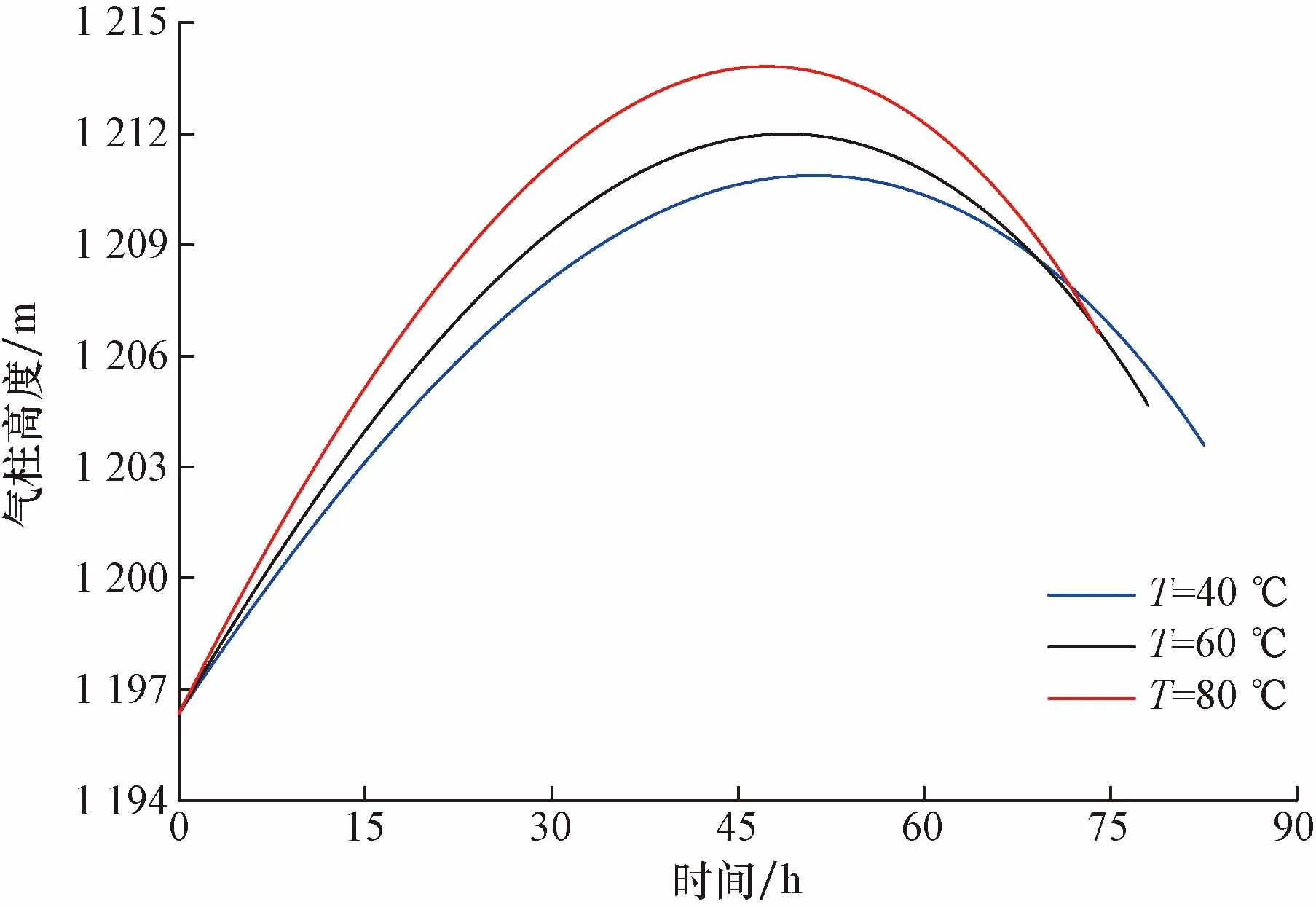
图9 初始环空温度对环空压力恢复中气柱高度影响Fig.9 Influence of initial annulus temperature on column height in annulus pressure recovery
不同环空压力对环空压力恢复过程影响如图10所示。可以看出,当Pa=29.57 MPa时,环空压力恢复到稳定值需约90 h,即平均环空压力恢复速度为0.585 MPa/h;当Pa=39.57 MPa时,经过74 h后环空压力达到稳定值,即平均恢复速度为0.576 MPa/h;当Pa=49.57 MPa时,环空压力恢复到稳定值需要约58 h,即平均恢复速度为0.563 MPa/h。由此可知,初始环空压力越大环空恢复速度越小。因此在保证井筒安全情况下,建议预留一定环空压力。
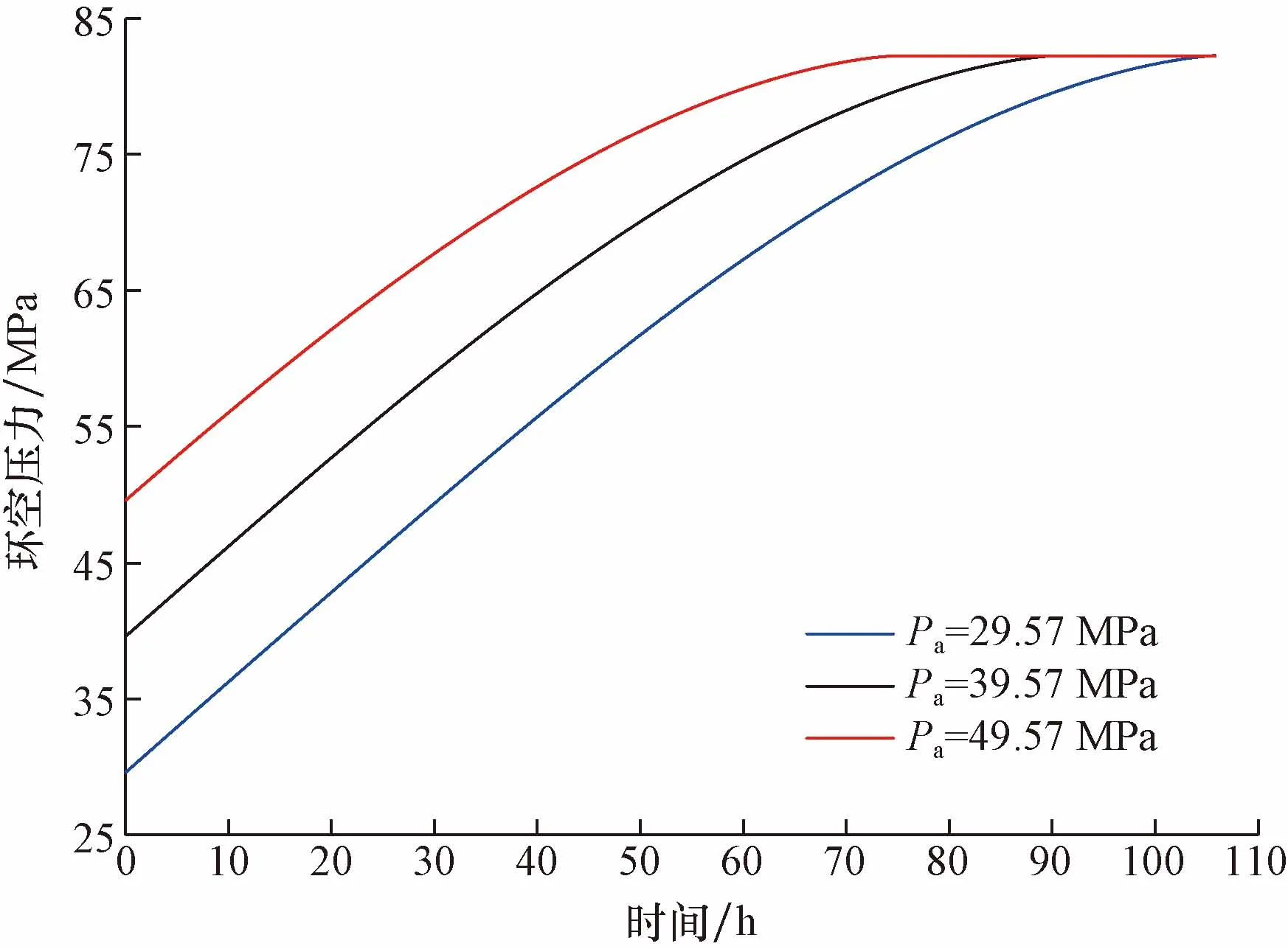
图10 初始环空压力对环空压力恢复过程影响Fig.10 Influence of initial annulus pressure on annulus pressure recovery process
图11为初始环空压力对环空压力恢复中气柱高度影响。可以看出,Pa=29.57 MPa,环空气柱高度最终为1 227.91 m,而当Pa=49.57 MPa时,经过环空压力恢复过程后气柱高度变为1 197.75 m。即环空气柱高度随环空压力的增大而减小。
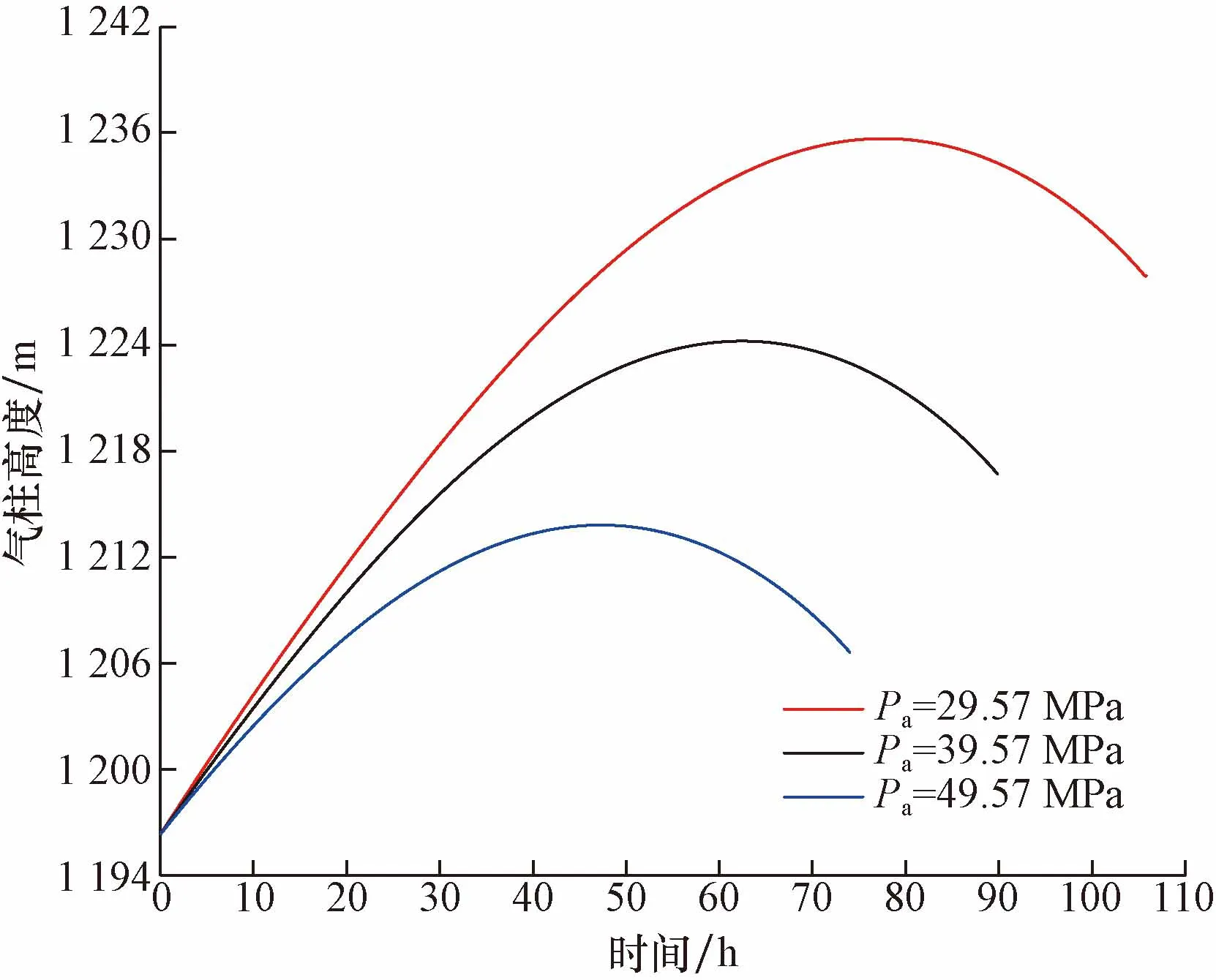
图11 初始环空压力对环空压力恢复中气柱高度影响Fig.11 Influence of initial annular pressure on column height in annular pressure recovery
3 结论
(1)在前人研究基础上,充分考虑温压耦合作用对环空液体热力学参数影响,建立了新的持续环空带压预测模型;利用该模型对A气井进行环空压力预测并与实测数据进行对比,所建模型预测平均精度高达96.05%,而未考虑温压影响的预测模型平均精度为94.86%,因此所建立模型预测数据更具有参考价值。
(2)利用所建立模型对A气井进行环空压力恢复过程模拟,结果表明该井环空压力稳定值为82.22 MPa,漏点最大流量为1 931.23 m3/d;环空压力恢复过程中环空气柱高度随时间增加呈先增大后减小趋势。
(3)利用模型对初始环空气柱高度、温度及压力可调控因素进行了环空压力及气柱高度敏感性分析,结果表明:预留一定环空气柱高度、压力及降低环空温度有利于降低环空压力恢复速度;气柱高度变化量随环空气柱高度及压力增大而减小,随环空温度增大而增大。
