基于双向耦合作用流场中异形筘内纬纱运动稳定性分析

2023-07-31肖世超方敬兵沈敏沈忱王真

科学技术与工程 2023年20期

肖世超,方敬兵,沈敏,沈忱,王真

(武汉纺织大学湖北省数字化纺织装备重点实验室,武汉 430200)

喷气织机具有速度快、产品适应性广及标准化的运转管理等优点,在无梭织机中占有不可替代的地位[1]。喷气织机的主、辅助喷嘴产生高速射流在异形筘槽内汇合,牵引纬纱纤维在异形筘道内飞行,纬纱头端波动太大碰到筘道断纬造成停机,直接影响织机效率及织物质量[2]。纬纱在气流载荷作用下会产生运动和变形,并且纬纱的运动反过来又会扰动引纬气流。因此,基于双向耦合作用研究柔性纬纱在异形筘道内流场的运动稳定性,对于提高喷气织机引纬速度、织物质量具有重要理论和工程价值。

流场和柔性纤维的耦合作用一直都是纺织机械研究领域的关键和难点问题,中外学者开展了大量研究。姚学昊等[3]针对涉及结构变形的流固耦合(fluid-structure interaction,FSI)问题,提出一种基于虚粒子和排斥力的近场动力学(peridynamics,PD)-光滑粒子动力学(smoothed particle hydrodynamics,SPH)耦合方法,提高计算精度。赵冉等[4]采用有限差分法模拟单根柔性纤维在剪切流中的运动,纤维在3种多场耦合模型中会呈现稳态运动的特性。未志杰等[5]建立了基于全隐式的有限差分法数值模拟器,以此证实了全流固耦合模型的准确性和可靠性。Tomohiro等[6]将纤维运动状态类比成二维风中旗帜进行有限有限元流固耦合仿真,很好地模拟出纤维的不同状态。Koohyar等[7]通过格子玻尔兹曼法数值模拟了纤维和流场间的相互作用。Pei等[8]采用N-S(Navier-Stokes)方程和任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)方程,研究了纤维的运动变形,但对纤维的本构方程、纤维的变形等都没有详细的剖析。Shen等[9]建立了经纱轴向和径向的运动方程,运用分离变量将时间变量与空间变量分离,给出了引纬过程中经纱的波动方程。陈雪善等[10]采用高速摄影系统拍摄了纱线在异形筘槽内流场中的运动状态,发现纬纱头部在行进中呈现旋转、卷曲波动状态。朱文静等[11]使用高速相机对纬纱在筘槽内运动进行了测试,表明纱线越细,飞行状态越稳定。金玉珍等[12]建立了二维的纤维与气流耦合方程,采用相容时间积分与迭代耦合算法,数值模拟了纤维在主喷嘴流场中的运动状态,表明纱线在气流作用下产生拉伸弯曲变形,自由端的弯曲变形明显比约束一端的大。李炯等[13]建立了二维纤维-气流耦合模型,数值模拟得到了不同时刻纤维的运动状态。郭臻等[14]建立了三维纤维-流场耦合模型,基于任意拉格朗日-欧拉法,数值模拟了纤维尾端在喷气涡流纺流场中的运动轨迹。

然而,现有研究局限于气流对柔性纱线的影响,并没有详细剖析纤维的运动变形对于流场的扰动,迄今为止,对于气流和柔性纬纱耦合作用机理尚未弄清。鉴于此,为研究柔性纤维与流场扰动耦合作用的机理,先构建单根纬纱纤维束本构模型,再建立气流-柔性纤维双向耦合的控制方程,采用拉格朗日-欧拉法数值模拟得到了柔性纤维在异形筘道内合成气流中的运动轨迹,讨论了辅助喷嘴不同出口形状、尺寸参数对纱线运动特性和异形筘道中合成瞬态气流的影响规律,可为流体动力型纺织机械的优化设计和工艺参数的设定提供理论参考。

1 柔性纤维-流场耦合动力学模型

1.1 柔性纤维本构方程

纬纱是由圆柱状的涤纶材料构成,由于纱线纤维束具有弹性,在引纬气流场中会发生拉伸、弯曲和扭转变形,纱线杨氏模量小,柔弹性好,常用本构模型可表示为

(1)

式(1)中:σ11、σ22为纤维束的主应力;ε11、ε12为纤维束受力产生的正应变;σ12为纤维束受到的切应力;γ12为切应变;kij为材料的刚度,可以用弹性模量和泊松比等参数进行调整。

纬纱纤维束在高速气流产生的摩擦力作用下产生位移,将纱线纤维束细分为若干个微元段,由两个刚性圆通过球窝关节连接而成(圆i和圆i+1纤维束),由牛顿第二定律得到微元段的方程为

(2)

式(2)中:m为圆的质量;t为时间;Xi为圆i的位置矢量;Xi+1为圆i+1的位置矢量 ;Fqi为微元段上的气流对纱线的牵引力;Fvi为球窝关节的黏弹力;Gi为微元段的重力。

1.2 气流-纤维束耦合控制方程

纱线在异形筘槽内流场中运动时,高速气流对纤维束的摩擦力,使得纤维束发生变形;然后,纤维变形反过来也会影响高速气流运动。因此,基于双向耦合方法数值求解气流-纤维束相互作用,采用N-S方程加入ALE方程作为控制方程迭代耦合。

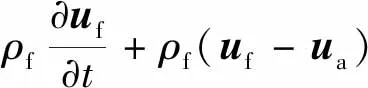
(3)

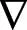
气流和纤维模型耦合界面上的结点同时满足运动学和动力学条件。

df=ds

(4)

nσf=nσs

(5)

式中:df和ds分别为纤维和气流在流固界面上的位移;σf和σs分别为流固交界面上的应力;n为界面上的法向向量。

2 柔性纤维-流场耦合动力学模型

2.1 柔性纤维本构方程

现有的辅助喷嘴主要有圆孔、三角形孔和星形孔等。根据现有的辅助喷嘴几何参数,建立辅助喷嘴三维几何模型,单圆孔、正三角形孔和星形孔辅助喷嘴几何模型,如图1所示。

α为喷向角图1 不同出口辅助喷嘴3D模型Fig.1 3D Models of auxiliary nozzles with different outlet

辅助喷嘴圆管区长度为12 mm,过渡区长度为10 mm,扁管区长度为18 mm。单圆孔直径为2.0 mm,入口直径为3.2 mm,壁厚0.4 mm。正三角形孔边长都为2 mm。入口直径为3.2 mm,壁厚0.4 mm。星形孔辅助喷嘴的结构,共由5排小圆孔组成,圆孔的直径为0.3 mm,由中心沿直线向外阵列,单排圆孔数为3个,共5排,每排相隔的角度为72°。

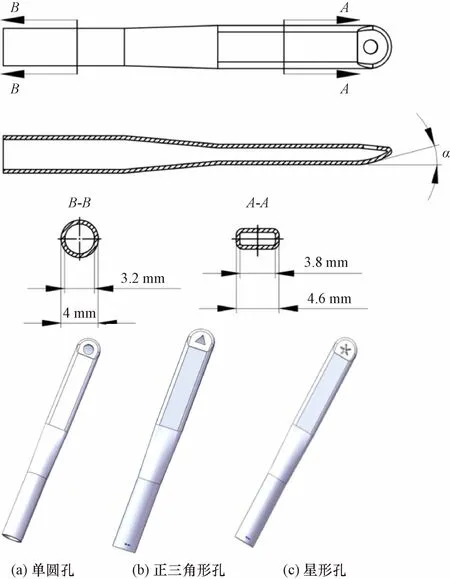
图2为气流-纤维束耦合作用的几何模型,定义气流场区域和纱线固体区域,流场区域包含3个辅助喷嘴射流汇入异形筘的区域,辅助喷嘴都具有相同参数,喷射角为6°、喷向角8°和辅助喷嘴间隔60 mm。异形筘流场内部的圆柱体代表纱线所占据的固体区域,引纬时纱线左端用携纱器将其夹持,所以对左端面进行固定约束,纱线头端在空间上可以自由运动。

图2 纱线-流场耦合几何模型Fig.2 Geometric model of the flow field of three auxiliary nozzles converging into the reed

2.2 气流-纱线双向耦合方程数值求解

采用ICEM软件对异形筘内三维流场进行网格划分,数值计算气流-纱线耦合作用,既要考虑异形筘微小流道内网格大畸变而导致计算的终止,又要考虑计算成本和结果精度,将辅助喷嘴入口流道划分为六面体结构网格,异形筘流道流域较为复杂采用四面体网格划分并加密,含有1.32×106个网格,保证流场各个网格单元密度大小相对匀称,纬纱纤维为具有较大长径比的圆柱体,用8结点六面体单元结构化网格,最终数量为1×105个,如图3所示。流场采用雷诺平均方程,选用k-ε湍流模型(k为湍动能,ε为耗散率),采用刚性壁面,气流入口压力0.3 MPa,出口压力为标准大气压,气流场主要数据如表1所示。利用FLUENT分析获得的数据设置为瞬态计算的初始条件,主要参数如表1所示。

表1 气流场主要参数Table 1 Main Parameters for air flow field

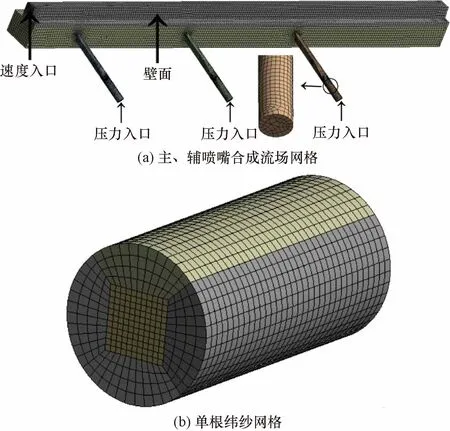
图3 三维流场和柔性纤维网格Fig.3 Synthetic flow field and yarn mesh model

纱线为涤纶材质,由于纱线在引纬筘槽内会产生弹性变形,忽略了纱线本身由捻度所产生的粗糙表面,只将纱线设置为弹性体,纱线长度为60 mm,头端直径为0.5 mm,纤维的纵向变形很小,将泊松比值设为0,纱线参数如表2所示。

表2 纬纱主要参数Table 2 Main parameters for weft

分析过程在纤维和气流交界面处进行应力与位移数据交互,通过交界面网格数据的实时传递,完成纤维和气流耦合作用的分析,计算完成后,纬纱全部单元的计算结果可以反映纤维整体运动轨迹。

3 实验原理

图4给出了捕捉纬纱运动形态的实验装置,由空压机、调压阀、主喷嘴、辅助喷嘴、异形筘及超高速摄影仪器组成。超高速摄影机型号为PHANTOM V711,拍摄快门速度最快可达5ns,可通过软件调节快门速度,并将拍摄得到的纱线运动变形的照片进行实时记录和保存,然后通过后处理软件Image Pro-Plus分析纱线在异形筘中随时间变化的位移情况。利用调压阀控制主喷嘴和辅助喷嘴的入口压力,纬纱纤维束从主喷嘴的导纱管中喷出,辅助喷嘴射流汇入异形筘道内,接力引纬。

图4 纬纱运动特性实验方案Fig.4 Experimental scheme of weft motion characteristics

4 结果与讨论

4.1 实验验证

为了验证数值方法的正确性,以圆形孔辅助喷嘴为对象,采用高速摄像机拍摄伸出主喷嘴出口10 mm的纬纱运动时的形态,如图5所示。可以看出,高射摄像机捕捉的纬纱弯曲变形,首先从尾端开始变形,延伸到纤维的中间部分,自由端弯曲变形最大,纤维在异形筘道内呈波浪形运动,数值仿真得到的纬纱运动轨迹与图像拍摄得到的纬纱运动位移趋势一致,波动幅度匹配,验证了数值结果的正确性。

图5 数值仿真与高速相机拍摄纬纱运动姿态Fig.5 Numerical simulation and high-speed camera shooting weft motion posture

4.2 不同辅喷对流场分布和纬纱运动稳定性影响

图6给出了分析流场-纬纱双向耦合作用,时间t=0.000 5 s时,不同形状的辅喷嘴射流进入异形筘槽内瞬态流场速度云图及纬纱运动状态。从图6中可以看出,高压空气刚从单圆孔射出,还没有进入到异形筘内,仅靠主喷射流牵引纬纱飞行;正三角形孔辅喷射流速度分布云图和单圆孔相似;星形孔辅射流已经扩散进入异形筘道内,对纬纱纤维束产生向上运动的摩擦力分量,避免纬纱头端弯曲变形碰到异形筘下壁,造成断纬。

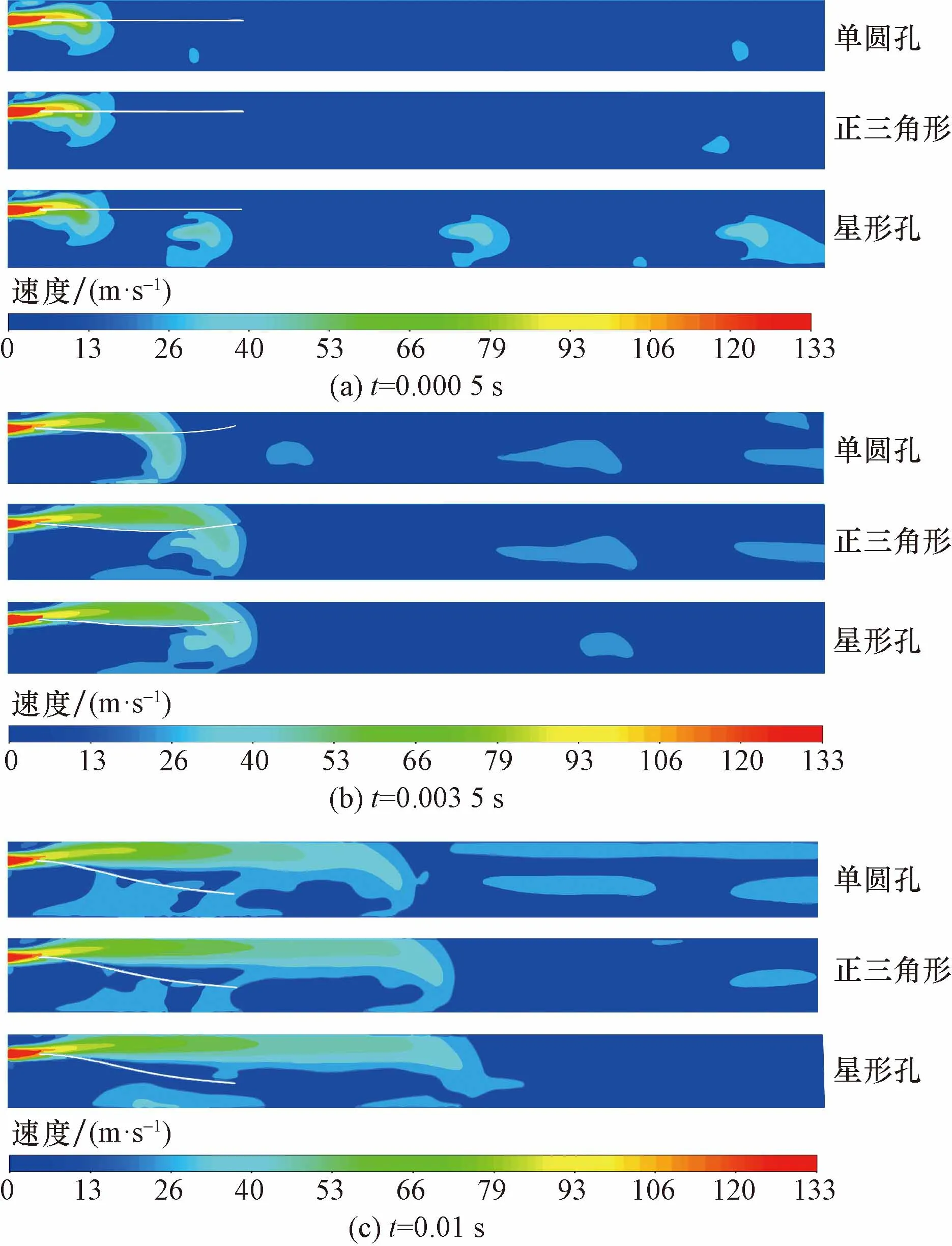
图6 不同辅助喷嘴合成流场速度云图和纬纱运动状态Fig.6 Synthetic flow field velocity contour and weft yarn bending deformation for different auxiliary nozzles

从图6(b)可见,当时间t=0.000 5 s时,纬纱运动产生弯曲变形扰动气流,不同形状辅喷合成流场的速度分布发生了变化,在异形筘道内,主气流势核长度明显增加,星形孔辅喷主气流势核长度最长,集束性最好,纤维与随着时间,发生弯曲变形,随着流场达到稳态,纤维呈正弦式上下摆动,并逐渐向下游游动,纤维在异形筘道中不断与壁面发生碰撞。

由于单根纬纱相对于流场整个流域微小,在整个气流场中难以定量分析,单独把单根纬纱纤维从合成气流场中分离进行分析,纱线初始z坐标均为0,在瞬态计算中记录纱线上均分的14个测量点不同时间下的坐标,比对z坐标绝对值大小与方差,确定纱线波动情况,并绘制检测点位移曲线。图7给出了时间t=0.01 s时,在不同形状的辅喷嘴合成流场中,纬纱运动轨迹。可以看出,在高速气流摩擦力作用下,纬纱出现了弯曲变形,从尾端开始逐渐增大,头端位移达到最大值。其中,在星形孔辅喷合成气流中,纬纱头端位移的幅值最小,引纬稳定性最好。

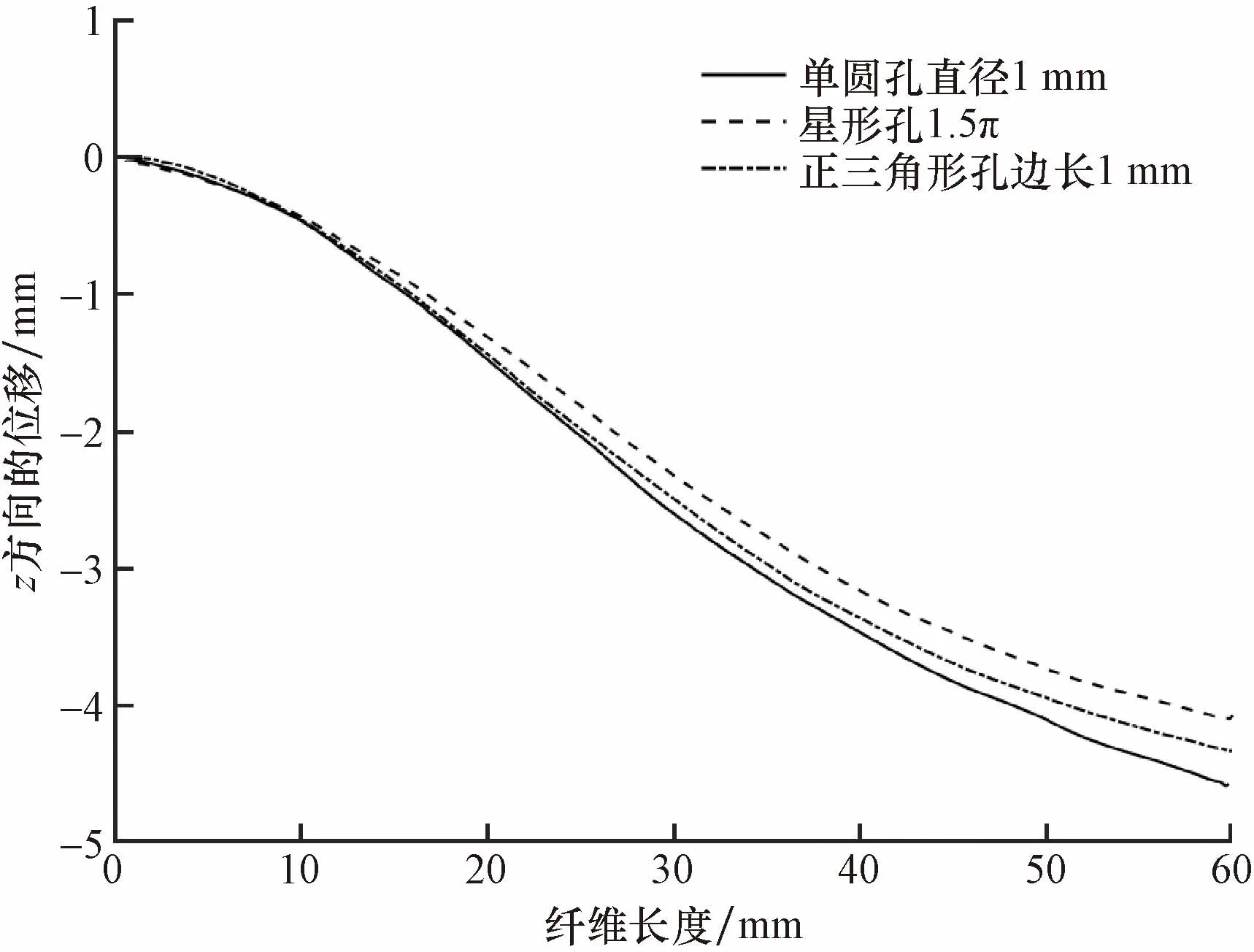
图7 t=0.01时纬纱在不同形状辅喷合成流场弯曲变形Fig.7 Bending deformation of weft yarn in the synthetic flow field of auxiliary nozzle with different shapes at t=0.01

4.3 不同尺寸辅喷对流场分布及纬纱运动稳定性影响

图8给出了数值分析流场-纬纱的双向耦合作用,不同直径单圆孔辅喷射流进入异形筘道内瞬态流场的速度云图及纬纱运动轨迹,单圆孔辅喷出口直径分别为1、1.5、2 mm,时间选取t=0.000 5、0.005、0.01 s。

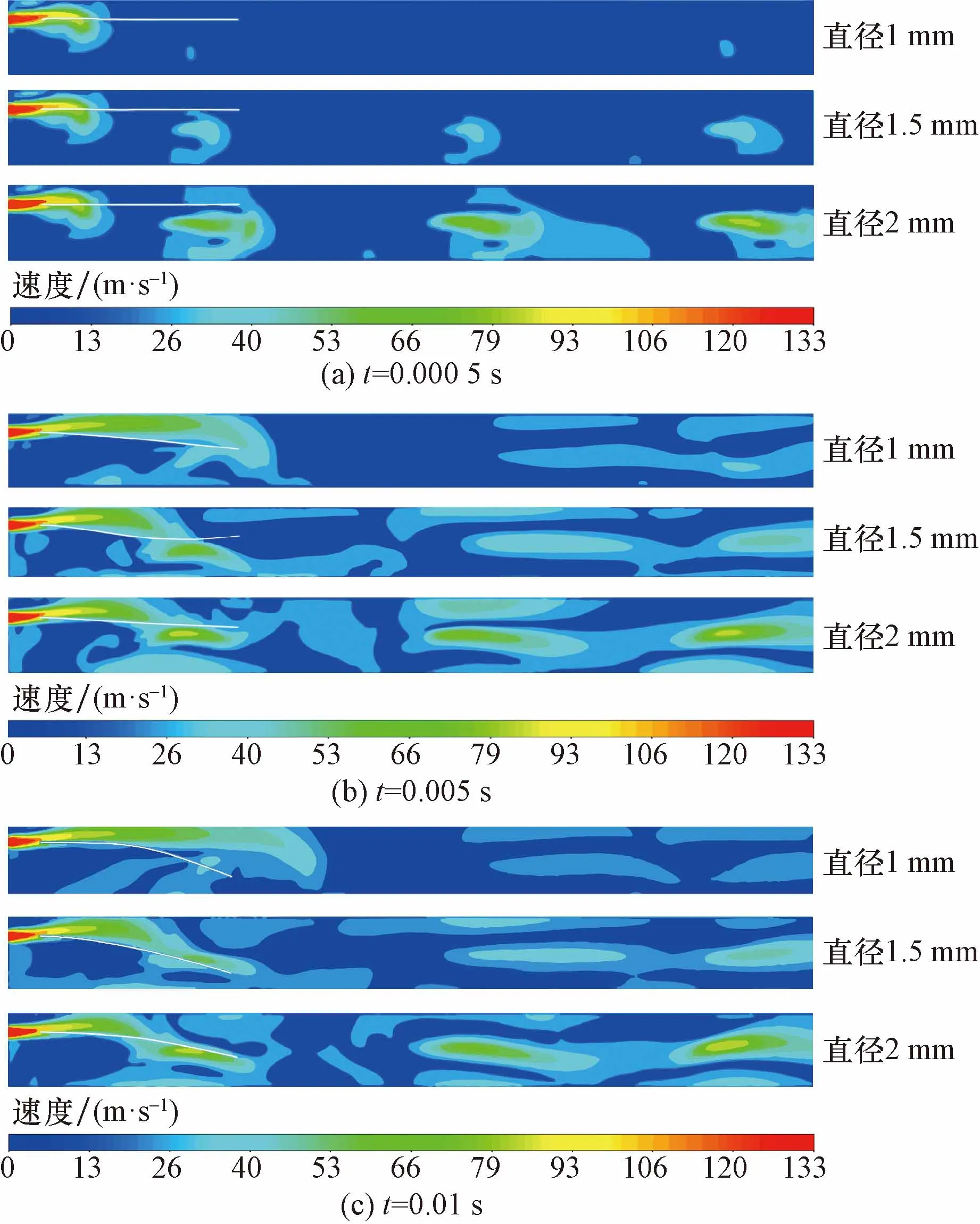
图8 不同直径单圆孔辅喷瞬态流场速度云图及纬纱状态Fig.8 Synthetic flow field velocity contour and weft yarn motional deformation at different times for different diameter ofcircular hole auxiliary nozzles

从图8(a)中可以看出,当t=0.000 5 s时,3种尺寸的单圆孔辅喷射流均未与主喷射流混合,直径1.5 mm的单圆孔辅喷射流一部分汇入异形筘道内开始扩散,核心区速度为40 m/s,直径2 mm单圆孔辅喷有较多气流汇入异形筘内,势核区域最长,核心区域速度达到80 m/s,对纬纱的摩擦力最大。

从图8(b)中可以看出,在t=0.005 s时,随着时间的增加,3种直径的单圆孔辅助喷嘴射流都已经在异形筘道内汇合,在气流摩擦力的作用下,纬纱产生明显的弯曲变形,湍流场速度分布也随之发生动态变化。从图8(c)中可以看出,当t=0.01 s时,喷口直径为1 mm的圆型辅助喷嘴合成流场中主气流区较最长,纬纱头端波动位移最小。

图9分析了流场-纬纱的双向耦合作用,正三角形孔辅喷出口边长分别为1、1.5、2 mm,时间取t=0.000 5、0.005、0.01 s。从图9(a)中可以看出,当t=0.000 5 s初始时刻,边长为1 mm和1.5 mm的正三角形孔辅喷射流均未进入异形筘槽内,仅由主喷射流牵引纬纱向前飞行,边长为2 mm的正三型辅角喷射流进入到异形筘道内,与主喷射流共同牵引纬纱向前运动;在图9(b)中,当t=0.005 s,3种尺寸正三角形孔辅喷射流已与主喷射流汇合,形成主射流的势核长度明显增长,速度也随之增大。此时,边长为2 mm的正三角形辅喷射流与主喷射流汇合形成的主气流势核长度最短,气流分布较为紊乱,对纬纱产生摩擦力的作用方向较多,整段纬纱弯曲变形较为复杂;在图9(c)中,当t=0.01 s时,边长为2 mm的正三角形辅助喷嘴的合成流场速度分布最为紊乱,边长1 mm和1.5 mm的正三角形的辅助喷嘴组合流场分布依然保持了较长的核心区域。

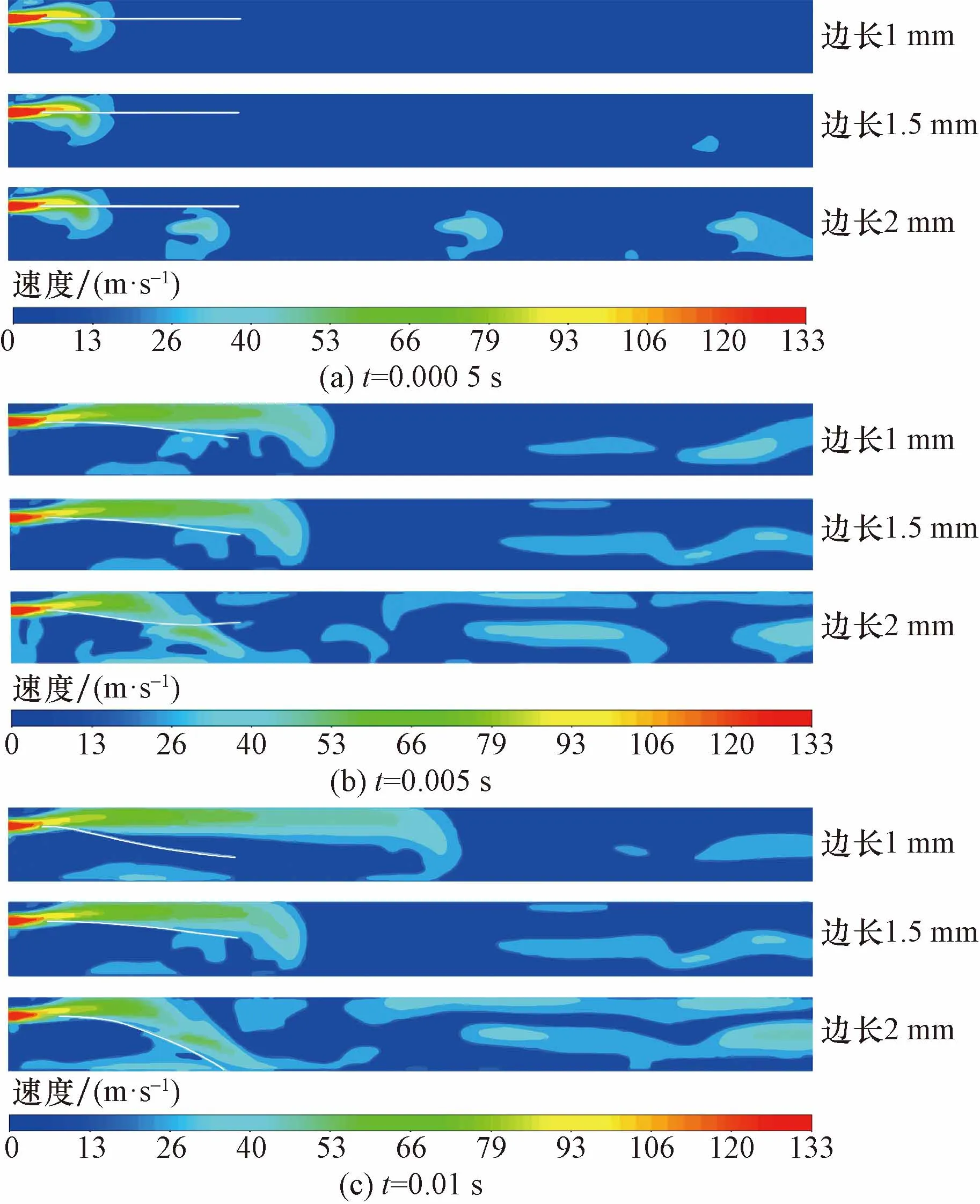
图9 不同边长正三角型辅喷的合成流场速度云图与纬纱弯曲变形Fig.9 Synthetic flow field velocity contour and weft yarn motional deformation for different side length of regular triangle auxiliary nozzles

图10显示了分析流场-纬纱的双向耦合作用,不同尺寸星形孔辅喷合成流场速度云图和纬纱运动轨迹,分别选取时间t=0.000 5、0.005、0.01 s。从图10中可以看出,随时间增加,主喷射流和辅喷射流逐渐汇合,形成的主气流势核不断增长,速度增大;边长1.5π mm的星形辅喷合成气流势核区域最长,边长2.7π mm星形孔辅喷合成气流长度其次,边长为3.9π mm星形孔辅喷合成气流的最短。

图10 不同周长星型孔辅喷合成流场速度云图及纬纱运动姿态Fig.10 Synthetic flow field-weft yarn coupling contour for different circumference of star hole auxiliary nozzles

4.4 不同尺寸辅喷对纬纱弯曲变形的影响

当时间t=0.01 s时,在直径为1 mm的单圆孔辅喷的合成气流中,纬纱的弯曲变形最小,运动稳定性最好。

图11显示了时间t=0.005 s时,纬纱在不同尺寸单圆孔辅喷合成流场中的位移。从图11可以看出,纬纱纤维尾端以微小的幅度摆动,头端以较大的幅度上下摆动,整段纤维呈现波浪式在异形筘槽内向气流下游运动,直径1 mm的单圆孔辅喷合成气流对纬纱运动的影响较小,纬纱位移最小,运动稳定性最好。

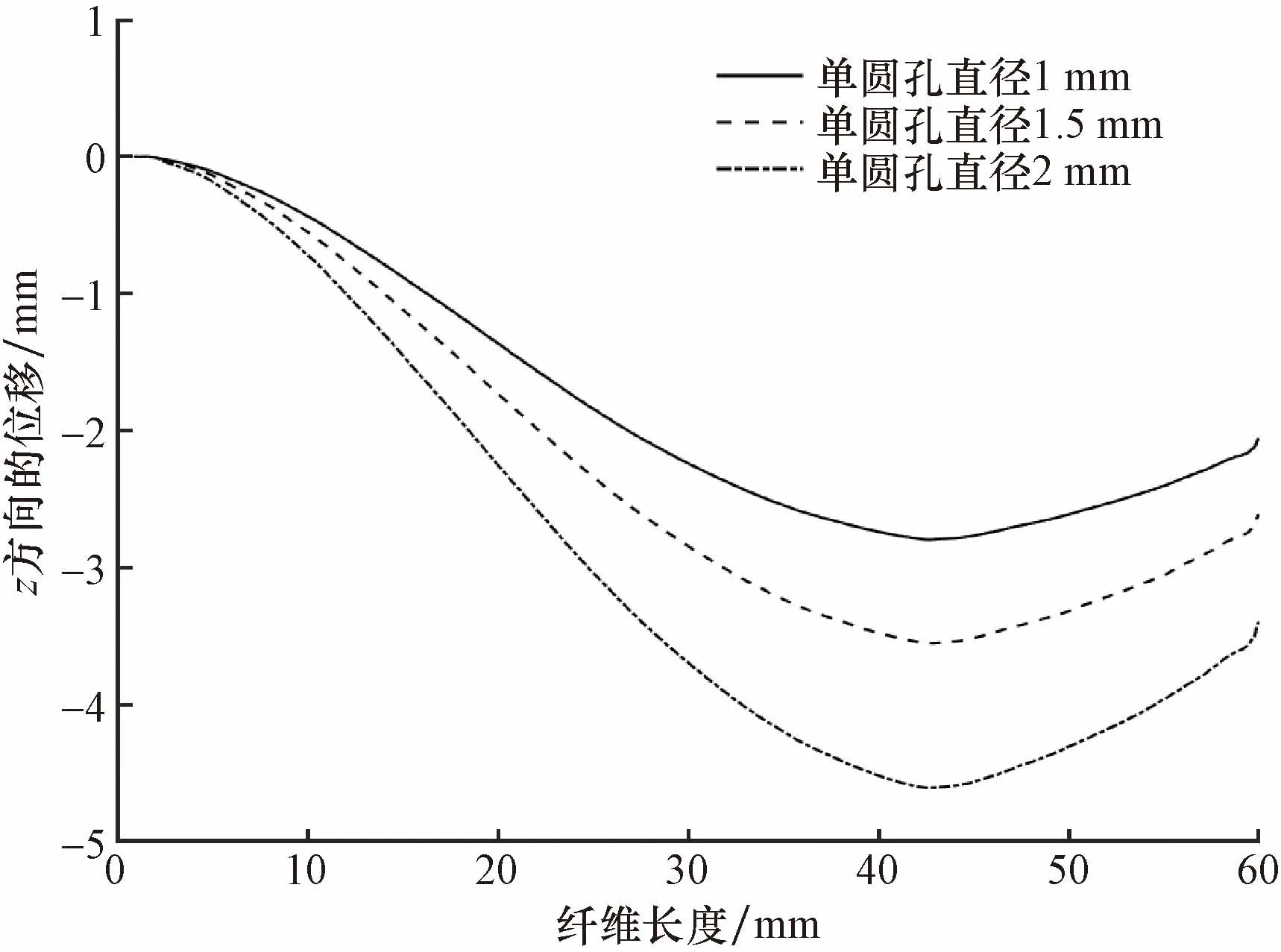
图11 t=0.005 s不同尺寸单圆孔辅喷合成流场中纬纱运动位移Fig.11 t=0.005 s weft movement in the synthetic flow field of single circular hole auxiliary nozzles of different sizes

图12显示了时间t=0.007 5 s时,纬纱在不同尺寸正三角形孔辅喷合成流场中的位移。从图12可见,边长为2 mm的正三角形辅助喷嘴合成流场中,纬纱头端位移接近了异形筘下侧边界位置,波动幅度最大,稳定性较差,若纬纱头端弯曲变形接触到异形筘片下侧,会造成断纬停机;在边长为1.0 mm的正三角形辅喷合成流场中,纬纱自由端的弯曲变形较小,头端距离异形筘片还有较大的间隙,引纬稳定性最好。

图12 t=0.007 5 s不同尺寸正三角形孔辅喷合成流场中纬纱运动位移Fig.12 Weft movement displacement in the synthetic flow field of different sizes of positive triangular hole auxiliary nozzles at t=0.007 5 s

图13显示了时间t=0.01 s时,纬纱在不同尺寸星形孔辅喷合成流场的位移,星形孔周长为1.5π、2.7π、3.9π mm。从图13可以看出,星形喷孔周长越小,在异形筘道内的合成气流中,纬纱的弯曲变形越小,运动稳定性更好,随着星形孔直径的增加,纬纱纵向位移增大,引纬稳定性降低。由此可知,设计高速引纬系统,喷口的尺寸不宜过大,有利于提高引纬稳定性。

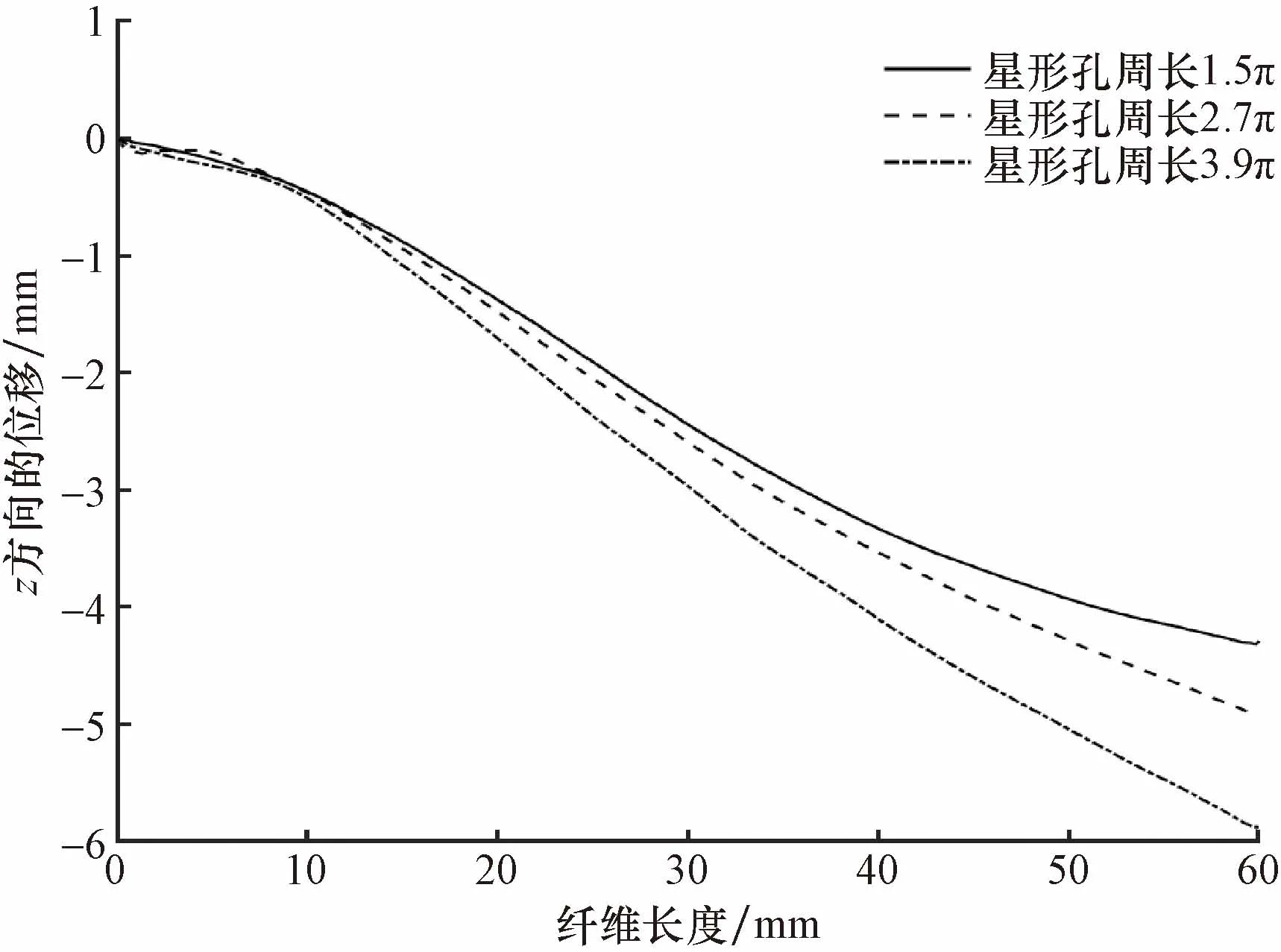
图13 t=0.01 s不同尺寸星形孔辅喷合成流场中纬纱运动位移Fig.13 Weft movement displacement in the synthetic flow field of different sizes of star hole auxiliary nozzles at t=0.01 s