我国小学数学教科书的建模研究

修前前　杨慧娟

［摘  要］ 数学建模能促进学生高阶思维能力发展，在基础教育中历来受到重视。研究者采用内容分析法，利用建模表征分析框架对小学数学3～6年级教科书（北师大版）进行研究，分析其建模表征特点并提出相应建议。

［关键词］ 小学数学教科书；建模；表征

一、研究背景

建模已經成为数学教育的关注焦点与核心理念，各国课程改革文件和课程标准也纷纷对数学建模做出明确要求。数学建模指运用数学模型对现实生活中的问题进行描述并根据模型解决问题，其本质是寻求并综合运用数学思想和数学方法，对实际问题进行分析和求解。建模的过程不仅能够增强学生对数学概念的理解，而且还能提高他们分析、解决实际生活问题的能力［１］。教科书是课程资源建设的核心资源，是实施教育教学的重要工具。我国中小学的课堂教学主要依据教科书实施教学，因此教科书肩负着体现建模思想、指导建模教学的重担。《义务教育数学课程标准（2022年版）》明确指出，教材要适当体现“问题情境—建立模型—求解验证”过程，并要求学生在五、六年级初步形成模型意识［２］。

国内对数学教科书的建模研究日益受到重视，西北师范大学李欣姝通过比较人教A版和北师大版高中数学教科书，发现北师大版教科书以专题形式呈现建模活动，更加注重学生建模能力的培养［３］。华东师范大学董玉成和徐斌艳比较了四种国内高中数学教科书（人教版、湘教版、苏教版、北师大版），发现我国教科书建模内容的整体特点：重模型应用而轻建模过程［４］。华东师范大学牛伟强通过对从1989年至2016年以来在中文核心期刊发表的有关中小学数学建模的文献进行研究后指出，我国中小学数学建模研究方法以思辨为主，缺乏实证研究和多样化的研究方法，并且对数学教科书中数学建模内容的研究相当匮乏［５］。分析数学教科书中的建模内容对判断教科书编排的科学性以及实施与评价数学建模教学具有重要意义。

国外学者对建模进行了比较系统的研究，美国密歇根大学施瓦茨将科学建模划分为模型实践和指导、激励实践的元认知，分别作为解释和预测科学模型的工具，包含构建、使用、评估、修改以及理解模型本质和目的六个子维度以及解释预测的四种水平，并以参与建模的五、六年级学生的课堂实例来证明其划分维度的科学性［６］。吉尔伯特和贾斯蒂将建模框架划分为原模型构建、原模型表征、模型检验和模型评估四个阶段，每个阶段包含了不同数量的组成元素，并且对各阶段所需技能进行较为全面的描述［７］。随后，贝尔岑基于模型存在概念化的层次，在建模能力框架中确立了五个维度三个层级，三个层级基于评估模型表象、评估模型构建过程、使用模型并评估其生产力的理论基础，体现了对五个维度描述的逐步加深［８］。

鉴于此，本文综合分析并整合学者的核心观点，构建数学教科书建模表征的二维分析框架，考察我国使用较为广泛的北师大版小学3～6年级数学教科书中模型选择、模型建立、模型验证和模型应用的实际情况，并分别从内容水平、呈现位置、表征方式三个横向维度分析其表征水平，以期为我国小学数学教科书的编写和改进提供循证依据。

二、研究方法

本研究采用内容分析法，依据数学建模分析框架及表征分析维度的二维分析工具，客观分析教科书内容，并对量化数据进行混合研究与循证描述。

首先，研究在参考有关学者建模框架的基础上，深入挖掘其中反映建模思想的共同核心要素并对其进行逻辑性整合，确立了本文的数学教科书建模分析框架（表1），共计4个一级指标，每个一级指标下设置4个子指标，共计16个二级指标。然后按照此框架对教科书文本所体现的数学建模指标进行纵向划分。

其次，本文结合建模分析框架和数学教科书的特点，开发了数学建模表征的内容分析标准量表，确定了数学教科书建模表征内容分析的主次分析维度和操作性定义（表2），并结合建模分析框架，应用该工具对教科书进行分析编码。主分析维度“内容水平”的四级量化评定方式具体如下：

①所占篇幅：水平I（0～50字）；水平II（51～100字）；水平III（101～150字）；水平IV（151字及以上）。

②由于出现频次和关联课数数量较少，因此1次为1级，4次以上统计为水平IV。

③描述水平：以二级指标“知识理解与提取”为例，水平I：只呈现相关知识；水平II：体现相关知识的理解与提取过程；水平III：相关知识的理解与提取两方面都能够体现；水平IV：对理解相关知识及之后的提取过程进行逻辑性表述。其他15个二级指标与“知识理解与提取”的四级量化评定方式一致。有关数学建模内容在“呈现位置”与“表征方式”的次分析维度中出现记为“1”，否则记为“0”。

此外，第八次课程改革后，我国教科书建设从“一纲一本”发展为“一纲多本”。由于北京师范大学出版社的数学教科书在发行量和使用效果方面影响较大，具有一定的权威性和代表性，并且考虑到小学中高年级的学生正处于由具体形象思维向抽象逻辑思维过渡的关键时期，本研究选取北师大版（2013年审定，2014年12月第1版）小学3～6年级数学教科书为研究样本，共计8册。

三、研究结果

（一）数学建模的内容水平

数学建模的内容水平反映教科书中建模内容的编排状况。

首先，数学建模内容全面但结构仍需完善。具体而言，“所占篇幅”“出现频次”“关联课数”呈现出相同的特点，即从模型选择到模型应用整体呈现上升趋势，模型建立水平最低；模型选择、验证、应用的“描述水平”基本一致（水平区间均为2.5～3），模型建立水平最高。进一步说，模型建立在教科书的篇幅、频次、关联课数中水平最低但描述水平最高。

其次，数学建模的内容水平在年级中整体表现为上升趋势，但上升幅度不一致且个别年级有所下降。模型选择在篇幅、课数、描述水平中，三到四年级大幅度上升，四到六年级持续性下降。可能由于模型选择在建模体系中处于最基础的位置，随着年级的升高，教科书对基础知识讲解详细程度以及对学生掌握程度的要求下降；模型建立、模型验证和模型应用在三到五年级上升，五到六年级下降。模型建立环节是数学建模的重中之重，是培养学生数学思维和能力的关键环节，六年级的下降应引起重视；四个环节的“关联课数”均比较均衡（图1）。

（二）数学建模的呈现位置

数学建模的呈现位置是指数学建模各环节在教科书中具体位置的呈现。

一方面，建模内容涉及位置广泛且体现建模内在逻辑。四个环节均表现为在“正文部分”内容呈现次数最多，然后依次是“例题习题”“引言背景”“课后拓展”，“边栏注释”最少，教科书正文作为课程教学的主体部分，内容呈现量比较多；此外，模型建立相关内容在“正文部分”的呈现量最多，在“课后拓展”“例题习题”等位置的呈现量最少。由于建模是比较复杂的过程，需要多方面能力的协调配合，故正文进行了较为详细的讲解，而拓展性内容涉及较少，“例题习题”部分主要关注知识的运用，因此表现为模型应用呈现次数最多。

另一方面，数学建模的呈现位置体现年级差异。在“正文部分”三年级内容最多，六年级最少，“例题习题”三年级最少，五年级最多。高年级正文内容有所减少而习题有所增加可能与年级的增长、学生认知水平的发展以及知识体系的构建有关；各年级在“引言背景”部分的内容比较均衡，无论年级高低都需要引言背景知识作为导入来帮助学生更好地学习新知；“边栏注释”大致体现出随年级升高而内容增多的特点，可能是由于内容知识的逐级丰富带来更多需要注意的细节；“课后拓展”整体均衡，高年级内容设置需要在此方面进行加强（图2）。

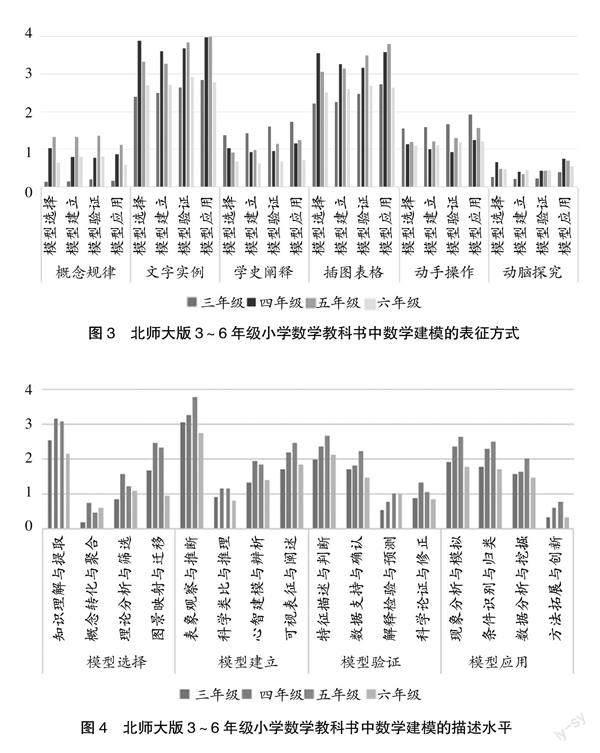
（三）数学建模的表征方式

数学建模的表征方式是指建模内容在教科书中清楚表达的形式化方式。

首先，数学建模的表征方式多样化，研究发现六种表征方式在分析样本中均被使用，其中以“文字实例”和“插图表格”方式表征的次数最为突出，“概念规律”和“动脑探究”表征次数最低。

其次，数学建模的表征方式体现年级差异，四年级的模型选择和模型建立在“文字实例”“插图表格”“动脑探究”中表征次数最多，而模型验证和模型应用则在五年级表征次数最为显著；三年级的“学史阐释”和“动手操作”表征次数最多，可能由于低年级教科书偏向于采用历史故事和动手操作的方式来激发学生数学学习的兴趣；“概念规律”的表征整体呈现逐年级增长趋势，但六年级有所下降，可能是由于三到五年级是不断输入新的数学知识、数学概念的过程，六年级学生进入总复习阶段，教科书中对新概念引入有所减少（图3）。

（四）数学建模的描述水平

“描述水平”是体现教科书编写科学性的重要维度，描述水平越高意味着教科书对知识讲解越深入，同时也意味著对学生掌握程度要求更高。

首先，各环节中培育学生高阶思维能力的内容较少。比如，模型建立中的科学类比与推理反映学生逻辑推理能力，但在模型建立中描述水平最低；模型验证的特征描述与判断描述水平最高，科学论证与修正的描述水平较低；模型应用中的方法拓展与创新描述水平最低。

其次，各二级指标描述水平整体呈逐年级上升趋势，但四年级水平高，六年级有所下降。比如，模型选择的四方面内容在四年级的描述水平最高，三到四年级上升幅度较大，四到五年级下降幅度较小，而五到六年级的下降幅度明显且图景映射与迁移下降幅度最大；模型建立中的描述水平到六年级下降幅度最大；模型验证的科学论证与修正在四年级教科书中的描述水平最高，三、五、六年级较为均衡；模型应用四方面内容在三到五年级均表现为水平持续性升高，到六年级则呈现出明显的下降。深层内容在中年级水平突出，高年级反而下降，不利于学生批判性思维与创造性思维的培育（图4）。

总之，教科书根据建模体系对内容进行了系统的安排，在内容水平上较大程度遵循了循序渐进原则；教科书内容分布广泛，从一节课例开始的“引言背景”部分到最后结束的“课后拓展”部分，均有内容知识呈现，且部分内容的呈现位置还根据年级特点做了差异性安排；同样，六种表征方式在样本中均有涉及，且除教科书编写中最主要用到的文字插图两种表征方式，其余四种辅助性表征方式的运用均关注了年级特点；各二级指标的描述水平总体表现出四年级水平突出，六年级有所下降，培养学生高阶思维能力方面内容水平偏低的特点。

四、结论与建议

为提高学生的数学建模意识、更好地培养学生的建模能力，建议教科书从加强数学建模内容布局的完善、不同年级中建模内容的安排以及强化学生高阶思维能力培育内容方面入手，提高学生的数学科学素养与分析解决实际问题的能力。

（一）遵循学科逻辑顺序，加强完善数学建模内容布局

从用“数学眼光”识别实际问题、用“数学语言”表达问题情境到用“数学思维”思考验证再到熟练运用“数学方法”解决实际问题，四个阶段由浅入深、环环相扣［９］。本研究选取的数学教科书总体体现出数学建模的系统性与逻辑性，只是数学建模的内容布局还需要进一步完善。以模型建立为例，教科书在这个环节对学生的掌握程度要求较高，但相关的讲解篇幅少、内容松散、螺旋程度低，会对学生的理解和掌握造成一定困难。因此，教科书需遵循学科内在逻辑，重视数学建模每一环节的内容布局，在提高建模关键环节描述水平的同时要加大相应内容的讲解篇幅、提高相关知识点的出现频次等以促进建模内容结构的完善，帮助学生更好地理解掌握建模。

（二）遵循学生发展规律，加强建模年级内容循证安排

对学生而言，数学建模思想的渗透、数学建模能力的培养应该遵循循序渐进、螺旋上升的原则。从研究结果来看，本研究所选取的教科书在一定程度上体现出关注学生年级差异的特点，但仍出现了跨越性较大、连贯性较弱，部分数学建模内容设置忽视学生认知发展和知识经验积累，与学生数学建模能力培养规律不适切的问题［１０］。以教科书中四年级和六年级的数学建模内容为例，四年级学生的逻辑思维能力以及数学建模的理解力正处于塑造发展时期，运用数学模型解决实际问题的系统性思维方式尚未形成，但四年级建模内容的设置在小学中高年级中却处于最高水平。同时，六年级数学建模教学内容水平表现出一定程度的下降，没有在五年级建模内容水平的基础上，进一步提高教科书数学建模内容水平。

因此，教师要遵循学生发展规律加强数学建模在不同年级内容的循证安排，让学生在数学建模的渗透中逐渐提高发现问题、提出问题、分析问题和解决问题的能力，增强学生数学应用意识和思维能力。

（三）匹配学生认知水平，强化高阶思维能力培育内容

教师了解学生现有认知发展水平，使教科书中数学建模内容水平的设置处于学生“最近发展区”，并适当增强数学建模中学生高阶思维能力培育内容的弹性，有利于调动学生学习积极性，促进学生逻辑推理和问题解决能力的良性发展［１１］。

本研究所选取的教科书没有充分考虑学生的层次性、忽视数学建模内容水平的弹性安排。以数学建模的描述水平为例，模型建立的科学类比与推理、模型验证的科学论证与修正以及模型应用的方法拓展与创新是各环节中最能体现高阶思维能力的项目，而这几个项目中的描述水平却较低，甚至有的处于各环节的最低水平，这不利于学生高阶思维能力的培育与发展。因此，可以通过脑科学和认知神经科学系统评估学生实际认知水平，充分考虑学生的层次性，加强教科书中数学建模内容的弹性设置，尽可能满足不同学生发展的需要，让学生都能接受良好的建模教育，促进学生高阶思维能力的发展［１２］。

参考文献

［１］ Ｌｅｓｈ，Ｒ.，＆ Ｚａｗｏｊｅｗｓｋｉ，Ｊ.Ｓｅｃｏｎｄ ｈａｎｄｂｏｏｋ ｏｆ ｒｅｓｅａｒｃｈ ｏｎ ｍａｔｈｅｍａｔｉｃｓ ｔｅａｃｈｉｎｇ ａｎｄ ｌｅａｒｎｉｎｇ：Ａ ｐｒｏｊｅｃｔ ｏｆ ｔｈｅ Ｎａｔｉｏｎａｌ Ｃｏｕｎｃｉｌ ｏｆ Ｔｅａｃｈｅｒｓ ｏｆ Ｍａｔｈｅｍａｔｉｃｓ.［Ｍ］. ＩＡＰ， ２００７.

［２］ 中华人民共和国教育部.义务教育数学课程标准（２０２２年版）［M］. 北京：北京师范大学出版社，２０２２.

［３］ 李欣姝. 高中数学教材“数学建模”内容比较研究——以人教Ａ版和北师大版必修教材為例［Ｊ］. 数学教学研究，２０２１，４０（０５）：３７－４３，４７.

［４］ 董玉成，徐斌艳. 我国高中数学教材中数学建模的处理——以人教版、湘教版、苏教版和北师大版教材为例［Ｊ］. 课程·教材·教法，２０１４，３４（１２）：５１－５６.

［５］ 牛伟强，张倜，熊斌. 中国中小学数学建模研究的回顾与反思——基于１９８９—２０１６年核心期刊文献的统计分析［Ｊ］. 数学教育学报，２０１７， ２６（０５）：６６－７０.

［６］ Ｓｃｈｗａｒｚ Ｃ Ｖ，Ｒｅｉｓｅｒ Ｂ Ｊ，Ｄａｖｉｓ Ｅ Ａ，ｅｔ ａｌ. Ｄｅｖｅｌｏｐｉｎｇ ａ ｌｅａｒｎｉｎｇ ｐｒｏｇｒｅｓｓｉｏｎ ｆｏｒ ｓｃｉｅｎｔｉｆｉｃ ｍｏｄｅｌｉｎｇ：Ｍａｋｉｎｇ ｓｃｉｅｎｔｉｆｉｃ ｍｏｄｅｌｉｎｇ ａｃｃｅｓｓｉｂｌｅ ａｎｄ ｍｅａｎｉｎｇｆｕｌ ｆｏｒ ｌｅａｒｎｅｒｓ［Ｊ］. Ｊｏｕｒｎａｌ ｏｆ Ｒｅｓｅａｒｃｈ ｉｎ Ｓｃｉｅｎｃｅ Ｔｅａｃｈｉｎｇ：Ｔｈｅ Ｏｆｆｉｃｉａｌ Ｊｏｕｒｎａｌ ｏｆ ｔｈｅ Ｎａｔｉｏｎａｌ Ａｓｓｏｃｉａｔｉｏｎ ｆｏｒ Ｒｅｓｅａｒｃｈ ｉｎ Ｓｃｉｅｎｃｅ Ｔｅａｃｈｉｎｇ，２００９，４６（０６）：６３２－６５４.

［７］ Ｊｏｈｎ Ｋ. Ｇｉｌｂｅｒｔ，Ｒｏｓáｒｉａ Ｊｕｓｔｉ. Ｍｏｄｅｌｌｉｎｇ－ｂａｓｅｄ Ｔｅａｃｈｉｎｇ ｉｎ Ｓｃｉｅｎｃｅ Ｅｄｕｃａｔｉｏｎ［Ｍ］. Ｓｐｒｉｎｇｅｒ，Ｃｈａｍ，２０１６.

［８］ ｚｕ Ｂｅｌｚｅｎ，Ａｎｎｅｔｔｅ Ｕｐｍｅｉｅｒ，Ｄｉｒｋ Ｋｒüｇｅｒ，ａｎｄ Ｊａｎ ｖａｎ Ｄｒｉｅｌ，ｅｄｓ. Ｔｏｗａｒｄｓ ａ ｃｏｍｐｅｔｅｎｃｅ－ｂａｓｅｄ ｖｉｅｗ ｏｎ ｍｏｄｅｌｓ ａｎｄ ｍｏｄｅｌｉｎｇ ｉｎ ｓｃｉｅｎｃｅ ｅｄｕｃａｔｉｏｎ［Ｍ］. Ｓｐｒｉｎｇｅｒ，２０１９.

［９］徐玥. 高中数学课程标准与教材中的建模核心素养编码研究［Ｄ］. 扬州大学，２０２０.

［１０］ 刘伟. 初中生数学建模能力培养研究［Ｄ］. 曲阜师范大学，２０２０.

［１１］ 童永健. 高中数学教材中数学建模内容的分析及再设计［Ｄ］. 华东师范大学，２０１６.

［１２］ 郭滕珞. 面向高阶思维发展的高中数学问题串教学研究［Ｄ］. 天津师范大学，２０２０.

作者简介：修前前（1999—），青岛大学师范学院硕士研究生，主要研究方向为小学教育、数学教育。

通讯作者：杨慧娟（1974—），青岛大学师范学院副教授，博士研究生，主要研究方向为数学课程与教学论、中小学数学教科书研究。