抓住转化 以不变应万变

王奇彦

(昆山市实验中学,江苏 苏州 215300)

数学思想是数学教学的精髓,培养学生的抽象思维和推理能力是初中数学课程的核心目标.在教学过程中,长期渗透数学思想,才能收到良好的教学效果.本文以初中数学教学内容为载体,浅谈笔者在教学中培养学生转化思想的几点体会.

1 在知识体系建构中渗透数学思想方法

数学教材中的概念、法则、公式、性质等知识都是有“形”的,而数学思想方法却隐含在数学知识体系里,是无“形”的,关键是教师如何去发现、发掘教材中蕴含的思想方法.转化思想作为最活跃、最常用的数学思想方法,在数学教学中进行推广是必须的[1].

古往今来,数学知识从来都不是孤立存在的,而是一脉相承、紧密联系的.数学知识和数学思想方法又是密不可分的,后者附着于前者而存在.初中生掌握的知识比较零散,初中数学教学更要帮助学生建构思维体系,学会进行数学思考.笔者在教学过程中注重学生思维体系的构建,注重学生解决问题策略的多样化,并渗透转化的数学思想方法.

例如,在用“边边边”证明三角形全等的教学中,笔者让学生根据已知条件画出相应的三角形,教师在观察学生作品的同时,提出问题:“我发现大家画的三角形的大小和形状都非常接近,是不是一样的呢?”请部分学生看看其他同学所画的三角形,回答老师的疑问,答案是肯定的.

另外,笔者请学生思考:采用什么方法可以说明大家画的三角形是全等的呢?学生畅所欲言,有的说采用“边角边”的方法证明,有的说采用“角边角”的方法证明,有的说采用“角角边”的方法证明,也有的说利用叠合法,把几位同学的三角形剪下来,看能否完全重合来判断全等.对以上这些方法,教师应充分肯定和重点说明.之后,师生共同总结利用“边边边”证明三角形全等的方法,完成证明过程的书写,初步形成对本知识点的建构.最后,提问学生:“刚才我们探究三角形全等的判断条件‘边边边’的证明方法时采用了怎样的数学方法呢?”学生举手发言,师生共同总结出运用了转化法、归纳法以及演绎推理等数学思想方法.

通过这样的教学活动,学生有效掌握了数学基础知识和基本技能,提升了其合作交流、主动探索的能力,学生的思维体系不断建构和完善,学生有能力发散性地思考问题,交流数学知识背后的数学思想方法.将证明“两个能够完全重合的三角形称为全等三角形”转化为只要证明“两个三角形三边对应相等”即可,将实际情况可能无法操作的定义转化为方便可行的判定定理.这就是转化思想的魅力之处.当然,转化不是解决数学问题的唯一方法,上述案例中还蕴涵了其他的思想方法.

2 化难为易——蕴涵在反比例函数中的“数”与“形”的转化

恩格斯指出:数学是研究数量关系和空间形式的科学.初中生的抽象思维还不够完善,在解决反比例函数与其他知识相结合的综合性数学问题时,教师应尝试用形象思维帮助学生理解与分析问题,在“数”与“形”的转化中,完成对此类问题的探究.

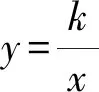
图1 例1题图

教学中,学生读完题目后,感觉无从下手.以下是笔者的教学实录和体会.

教师:本题求什么?

学生1:k.

教师:k是什么?

学生2:反比例函数的比例系数.

教师:同学们之前是怎么求的?

学生3:已知反比例函数图像上一点的横、纵坐标或满足反比例函数解析式的一组x和y的对应值.

教师:一定要知道x与y各是多少吗?还是知道某种关系就可以了?

学生4:不一定,因为反比例函数的第三种表达式是xy=k,只需求得一组x与y的积即可.

教师:其他同学赞同吗?其他学生表示赞同.

通过提问逐步启发,学生明白了k的值等于符合反比例函数解析式的一组x与y对应值的乘积,将求k的问题转化成了求一组x与y对应值乘积的问题,这是求解本题的关键之一.

教师:同学们能从题设中看出什么隐含的条件?

学生5:由AO=AB可知△ABO是等腰三角形.

学生6:△ABO的面积为12,为利用这一条件,需作△ABO的高.求三角形的面积需要作高.

学生7:点D是AB的中点,想到过点A作△ABO的高,过点D作x轴的垂线段DE,分别交x轴于点C和E.教师板书添加辅助线,如图2所示.

图2 添加辅助线后的图形

教师:这样添辅助线能帮助我们解决问题吗?

3 实际问题数学化,在转化中增强学生的数学应用意识

《义务教育数学课程标准(2022年版)》在基本理念中指出:“数学是人们生活、劳动和学习必不可少的工具,能够帮助人们处理数据、进行计算、推理和证明,数学模型可以有效地描述自然现象和社会现象.”重视数学知识的应用,加强数学与实际的联系,是其强调的重点之一.在解决实际问题时,教师要引导学生重在分析,把实际问题转化为数学模型,培养学生应用数学知识解决实际问题的能力[2].

例2 某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数,其图像如图3所示.

图3 例2题图

(1)你能写出这个函数的解析式吗?

(2)当气球内的气压大于140 kpa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?

在本题的探讨中,学生看到题设就知道是反比例函数.有学生能准确地说出图像是比例系数k>0时,反比例函数图像位于第一象限的一支曲线.学生自然将其与反比例函数这一数学模型联系在了一起.

教师:第一问怎么求?

教师:为什么这样代入点A的坐标求出的k就是反比例函数的比例系数?

学生1:因为点A在反比例函数的图像上,它的横、纵坐标是满足解析式的一组x与y的对应值.

教师:你们觉得呢?学生表示赞同.

教师:第二问有没有关键词,应该怎么做?

学生2:问题中含有“大于”“不小于”两个关键词,用不等式解决.

教师:其他同学跟他想法一样吗?有学生赞同.

教师:大家自己试着求一求.

学生3:按照题设列出的是不等式,还没有学过.其他同学也遇到了困难.

教师:如图3,y表示气压,从图像上看,“气压大于140 kpa”表示哪一段函数图像呢?体积呢?

学生4:从图像上看,“气压大于140 kpa”表示纵坐标大于140 kpa时对应的部分函数图像,即图中所画水平直线上方的部分函数图像.为了安全,气体的体积应该不小于水平直线与反比例函数图像交点的横坐标.

师生共同得出,水平直线与反比例函数图像交点的横坐标就是题目要求的安全体积的最小值.教师引导学生总结将实际问题转化为数学问题,用数学知识解决实际问题的思维过程,如图4所示.

图4 解决实际问题的基本思维过程

本案例中,学生与教师共同探讨,交流互动,遇到困难时能迎难而上,探寻正确的方法.最后还能总结实际问题与数学问题之间的关系,丰富了学生数学学习的维度,让学生经历数学交流与反思的过程,总结转化的数学思维方式,逐步建构起数学思维体系,将数学知识真正运用于实际生产生活中.

正如著名的数学家乔治·波利亚所云:“完善的思想方法犹如北极星,许多人通过它而找到正确的道路.”在平时教学中,我们要努力挖掘数学知识中所蕴涵的转化思想及其它数学思想,把握运用数学思想解决问题的机会,增强学生主动运用数学思想的意识,提高学生的数学能力,提升学生的数学素养,促进学生的全面发展.