基于强化学习的禁飞区绕飞智能制导技术

惠俊鹏，汪韧，郭继峰

1.哈尔滨工业大学 航天学院，哈尔滨 150006

2.中国航天科技创新研究院，北京 100176

高速飞行器因临近空间的复杂不确定性，滑翔段制导技术的研究面临诸多挑战［1］。随着临近空间飞行任务的多样化，飞行器不仅需要满足一般的过程约束和终端约束等要求，还需要满足规避禁飞区的要求。禁飞区指飞行器飞行过程中不允许通过的位置区域，例如地缘政治禁止通过的区域等。禁飞区绕飞制导技术的研究主要分为2 类：一是离线轨迹规划；文献［2-4］基于优化理论，将飞行器禁飞区绕飞问题转化为轨迹优化问题，可实现全局轨迹的优化求解以及最优绕飞策略的生成。文献［5］提出一种基于改进稀疏A＊算法的禁飞区绕飞轨迹规划方法，该方法基于最小转弯半径约束进行节点拓展，有效提高了搜索效率，能够成功完成绕飞轨迹规划。二是在线禁飞区绕飞制导，赵江［6］、Liang［7］和Zhang［8］等提出了一种考虑禁飞区规避的预测校正制导方法，纵向制导采用落点误差预测与指令校正相结合的方式更新倾侧角的幅值，侧向制导设计了一种倾侧角反转逻辑的切换机制，利用航向角误差走廊和航向角导向区域控制飞行器的侧向运动。赵亮博等［9］开展了基于虚拟目标导引的高速飞行器禁飞区规避制导方法研究，结合Dubins 曲线轨迹规划方法与比例导引方法实时跟踪虚拟目标，实现飞行器对禁飞区的规避制导。章吉力等［10-11］对禁飞区影响下的空天飞机可达区域计算方法进行了研究，从极限绕飞轨迹与禁飞区的切点出发，提出绕过禁飞区后的可达区域计算方法，并研究一种考虑禁飞区规避的分段预测校正制导方法。文献［12-13］提出了一种基于虚拟多触角探测的航路点规划机动制导策略，通过飞行器最大转弯轨迹计算速度-剩余地面距离-航向角约束，并采取双模式多触角探测反馈的方法进行机动制导策略的设计，可有效地解决机动制导过程中的多约束问题。文献［14］提出基于人工势场的侧向制导方法，适用于处理航路点约束和禁飞区约束问题。Yu 等［15］设计了一个复杂但严格的框架，获得拟平衡滑翔条件下禁飞区绕飞的解析制导指令，并通过仿真验证了该方法可处理多个禁飞区的绕飞任务。

近年来，随着人工智能的快速发展，强化学习技术大量应用于解决智能体的决策问题［16］，具有代表性的强化学习算法有深度Q 网络（Deep Q Network，DQN）［17］、深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）［18］、软动作-评价（Soft Actor-Critic，SAC）［19］和近端策略优化（Proximal Policy Optimization，PPO）［20］。强化学习技术在制导控制领域的应用尚处于初步阶段。文献［21-27］研究了基于DDPG、DQN 和PPO 等算法的智能制导技术，在纵向制导中计算倾侧角幅值，抽象横向制导倾侧角反转逻辑为马尔可夫决策问题，使得飞行器初步具备了自主决策能力。在姿态控制方面，文献［28-31］在传统控制的基础上，进一步利用强化学习算法实现了从飞行器位置、速度和姿态角等信息到控制量的端到端飞行控制。

传统高速飞行器禁飞区绕飞方法存在2 方面的不足：一是优化类方法存在迭代计算量大、收敛速度慢等问题，难以满足在线应用的实时性要求；二是预测校正制导方法在纵向制导中仅以中末交班点信息校正倾侧角的幅值，未综合考虑禁飞区的位置信息和中末交班点信息，在横向制导中需要基于人工经验设计飞行走廊参数，对于突现的禁飞区适应能力差，影响高速飞行器在不确定飞行环境中完成任务的成功率。

针对高速飞行器禁飞区绕飞问题，通过智能技术的赋能，提升高速飞行器对不确定禁飞区绕飞的适应能力。具体问题为：

1）参数设置

飞行器的再入初始点参数和禁飞区的位置参数在合理的范围内随机设置，中末交班点的位置固定，目的是希望以随机的再入初始点为起滑点，成功绕飞随机位置的禁飞区，且能精确到达固定的中末交班点。

2）飞行器的飞行轨迹可分为如下3段：

第1 段，飞行器从再入初始点开始并不清楚前方是否有禁飞区，在尚未发现禁飞区时，以中末交班点为滑翔段目标点，基于预测校正制导方法实时解算制导指令；第2 段，当飞行器与禁飞区中心点的距离小于禁飞区半径的2.5 倍时，飞行器探测到前方有禁飞区，开始实施机动绕飞，该段采用智能制导方法，以飞行器相对禁飞区和中末交班点的状态信息为输入变量，利用训练的智能制导模型实时输出绕飞时的制导指令；第3 段，当飞行器与中末交班点的距离小于禁飞区中心点与中末交班点的距离时，认为禁飞区绕飞结束，绕飞结束后继续采用预测校正制导方法控制飞行器精确到达中末交班点。

本文的立意主要体现在以下2 个方面：

1）提出“预测校正制导—基于监督学习预训练倾侧角制导模型—基于强化学习进一步升级倾侧角制导模型”逐级递进的禁飞区绕飞智能制导研究框架。首先，设置高速飞行器合适的初始点和禁飞区的参数范围，基于传统预测校正制导方法，生成大量的禁飞区绕飞样本轨迹；其次，利用监督学习方法和生成的样本轨迹对倾侧角制导模型进行预训练，其目的是通过领域知识引导绕飞策略的搜索，使得基于监督学习方法训练出的制导模型对禁飞区的绕飞效果最大程度逼近基于预测校正制导的绕飞效果。

2）在监督学习的基础上，进一步利用强化学习技术在智能决策方面的天然优势，摆脱传统预测校正制导方法对倾侧角解空间的约束，通过飞行器与环境大量交互“试错”，并借鉴人类基于反馈来调整学习策略的思想，设置有效的奖励（反馈）引导，利用强化学习中PPO 算法进一步升级禁飞区绕飞倾侧角制导模型。一方面利用智能技术充分挖掘高升阻比飞行器强大的横向机动能力，在不同倾侧角下其横向机动距离可以从几百公里跨越到上千公里，利用智能制导模型将倾侧角的幅值和符号一并输出，具有更大的探索空间，期望产生更优的绕飞策略；另一方面受飞行器的能量约束，在绕飞时需综合考虑禁飞区约束和滑翔终端约束，确保绕飞后具备足够的能量精确到达中末交班点，从而满足未来飞行器智能决策系统对不确定场景的适应性需求。

围绕基于强化学习的禁飞区绕飞智能制导技术开展研究，第1 节建立了高速飞行器的动力学模型；第2 节研究了禁飞区绕飞智能制导模型的设计；第3 节深入研究基于监督学习的禁飞区绕飞倾侧角制导模型的训练；第4 节在第3 节研究的基础上，进一步深入研究基于强化学习的禁飞区绕飞倾侧角制导模型的升级训练；第5 节给出仿真、对比与结果分析；第6 节为结论。

1 高速飞行器动力学建模

1.1 高速飞行器运动模型

高速飞行器三自由度动力学方程为

式中：r为地心距；θ和ϕ分别表示飞行器的经纬度；V为飞行速度；γ和ψ分别表示飞行器的航迹角和航向角；σ表示倾侧角；m为飞行器的质量；g为重力加速度；L和D分别表示飞行器受到的升力和阻力［32］。

1.2 再入制导约束

高速飞行器在飞行过程中需满足多种约束条件，主要包括：

1）硬约束条件

硬约束条件是指飞行器飞行过程中需要满足的热流率、过载和动压等约束条件，其表达式为

2）中末交班点约束条件

中末交班点约束是指滑翔段和末制导段的交班点满足高度、速度、经纬度等约束，可表示为

式中：tf、rf、Vf、θf和ϕf分别表示中末交班点的时刻、地心距、速度、经度和纬度，tf不固定，rf、Vf、θf和ϕf是预先设置的。

3）禁飞区约束条件

一般采用无限高的圆柱模型来描述禁飞区约束，再入飞行轨迹不能与该圆柱相交。禁飞区约束可建模为

式中：R0为地球半径；θNFZ、ϕNFZ和rNFZ分别表示禁飞区中心的经度、纬度和半径。

2 禁飞区绕飞智能制导模型的设计

2.1 研究框架

本文借鉴Alpha Go［33］的思想，将监督学习技术和强化学习技术融合应用于禁飞区绕飞制导中，主要包括3 个步骤，如图1 所示。

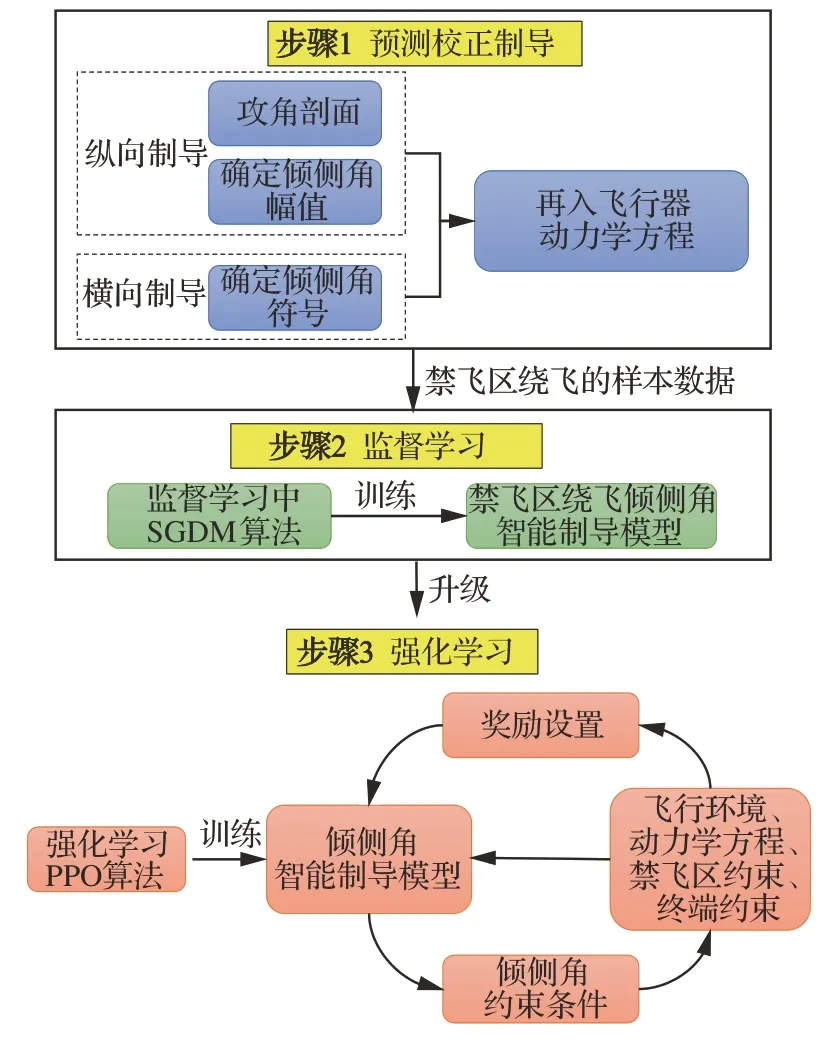
图1 高速飞行器禁飞区绕飞智能制导研究框架Fig.1 Research framework of intelligent guidance of re‐entry vehicles for avoiding no-fly zone

步骤1预测校正制导

设置飞行器再入初始点和禁飞区的参数范围，基于传统预测校正制导方法，生成大量的绕飞样本轨迹。

步骤2监督学习

建立禁飞区绕飞倾侧角智能制导模型，利用监督学习中带有动量的随机梯度下降（Stochas‐tic Gradient Descent with Momentum，SGDM）算法［34］和步骤1 产生的绕飞样本轨迹，训练倾侧角智能制导模型。

步骤3强化学习

在步骤2 基于监督学习训练出的禁飞区绕飞倾侧角智能制导模型的基础上，利用强化学习在智能决策方面的优势，在禁飞区约束、终端约束、过程约束下通过飞行器与环境进行大量交互，并借鉴人类基于反馈来调整学习策略的思想，设置有效的奖励（反馈），利用强化学习中PPO 算法［20］进一步训练禁飞区绕飞倾侧角制导模型，实现飞行器基于实时的状态信息在线决策禁飞区绕飞所需的倾侧角幅值和符号指令。该方法一方面充分挖掘高升阻比飞行器强大的横向机动能力，另一方面受飞行器的能量约束，确保绕飞后具备足够的能量精确到达中末交班点。

2.2 禁飞区绕飞倾侧角智能制导模型

禁飞区绕飞示意图如图2 所示。其中，C是高速飞行器的当前位置；T为中末交班点的位置；Z为禁飞区的中心；M为C点与禁飞区切线的交点。过C点作禁飞区的切线CM和CN，CM与北向的夹角为ψM。

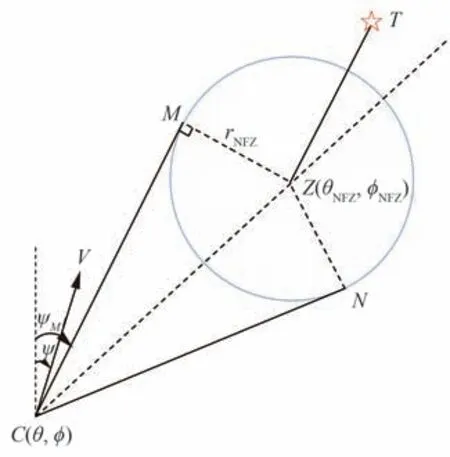
图2 禁飞区绕飞示意图Fig.2 Diagram of avoiding no-fly zone

禁飞区绕飞倾侧角智能制导模型如图3 所示，其中制导模型的输入为飞行器的状态向量，定义状态向量为

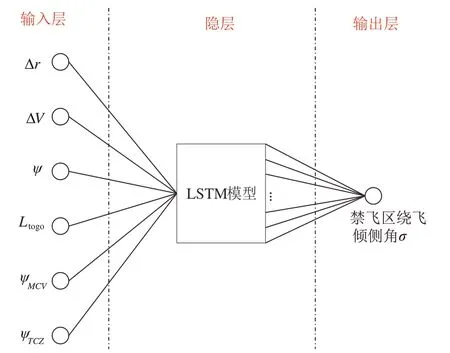
图3 基于LSTM 的禁飞区绕飞倾侧角制导模型Fig.3 Bank angle guidance model avoiding no-fly zone based on LSTM

式中：Δr=r−rf表示t时刻的地心距与中末交班点地心距的差；ΔV=V−Vf表示t时刻的速度与中末交班点速度的差；Ltogo表示t时刻飞行器距离中末交班点的剩余航程：

s(t)的后2 个变量（ψMCV，ψTCZ）为飞行器相对禁飞区的状态变量。由图2 可以看出，在禁飞区绕飞时需要考虑：

1）判断从哪一侧规避禁飞区，ψTCZ=ψT−ψZ表示CT与北向的夹角ψT与CZ与北向的夹角ψZ的差。当ψTCZ<0 时，从禁飞区左侧绕飞；当ψTCZ>0 时，从禁飞区右侧绕飞。

2）判断速度V的方向是否指向禁飞区，ψMCV=ψM−ψ表示CM与北向的夹角ψM与飞行器航向角ψ的差。当飞行器速度方向指向禁飞区外侧时，ψMCV>0；当飞行器速度方向指向禁飞区时，ψMCV<0。

禁飞区绕飞倾侧角制导模型的隐层为长短期记忆网络（Long Short-Term Memory，LSTM）模型［35］，隐层的节点数为64 个，隐层到输出层是全连接，输出为倾侧角σ。

从智能决策的角度来说，飞行器绕飞决策属于典型的序贯决策问题，每一时刻决策倾侧角时不仅取决于飞行器当前时刻的状态，还与上一时刻的倾侧角有关。因而在决策倾侧角时需要考虑相邻时刻间的状态关系，而这也恰好是LSTM 所具有的独特优势，是解决序贯决策的经典模型，因而选择基于LSTM 构建禁飞区绕飞倾侧角制导模型。

2.3 倾侧角幅值的约束

基于LSTM 模型输出禁飞区绕飞的倾侧角需满足再入过程的硬约束条件。文献［32］将再入过程的硬约束条件转化为对倾侧角幅值的约束：

式中：CL和CD分别为升力系数和阻力系数；S为特征面积；分别为热流率、过载和动压约束下飞行器倾侧角的上界。在基于LSTM 模型输出禁飞区绕飞倾侧角幅值的基础上，进一步利用式（7）对倾侧角进行限制，使其满足硬约束条件。

3 基于监督学习的禁飞区绕飞倾侧角制导模型的训练

训练过程分为2 步：一是禁飞区绕飞训练样本的生成；二是禁飞区绕飞倾侧角制导模型的训练。

3.1 训练样本的生成

选取美国通用航空飞行器CAV-H 为研究对象，基于预测校正制导方法产生禁飞区绕飞的样本数据。参数设置如下［36］：

1）飞行器参数

质量m=907.20 kg，特征面积S=0.483 9 m2，过程约束中最大允许热流率，最大允许过载nmax=3g，最大允许动压qmax=100 kPa。

2）中末交班点参数

高度hf=23 km，经度θf=50°，纬度ϕf=0°，速度。

3）攻角剖面

4）飞行器再入初始点和禁飞区的状态参数设置如表1 所示。

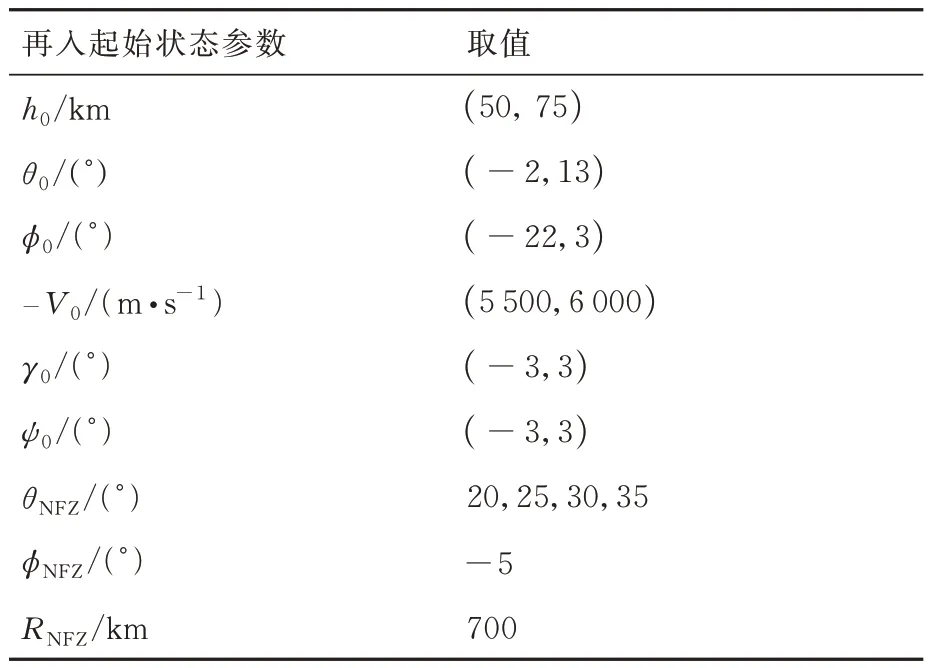
表1 飞行器再入初始点和禁飞区的参数Table 1 Parameters of initial state and no⁃fly zone of flight vehicle

在上述参数范围内随机设置飞行器的再入初始点和禁飞区参数，在预测校正制导下可以获得大量的绕飞轨迹数据。在打靶试验后，总计生成2 048 条飞行轨迹，从禁飞区左侧和从右侧规避的飞行轨迹各1 024 条。符合中末交班点约束和禁飞区约束的飞行轨迹共1 309 条，其中从左侧规避弹道623 条，从右侧规避弹道686 条，如图4 所示。从1 309 条飞行轨迹数据中，随机抽取1 200 条飞行轨迹数据组成样本集，其中840 条飞行轨迹用作监督学习时的训练集，180 条飞行轨迹用作验证集，剩下的180条飞行轨迹用作测试集。

图4 通用航空飞行器H 从左右两侧规避禁飞区的绕飞轨迹Fig.4 Subsatellite track formed by common aero vehicle-H avoiding no-fly zone from left and right side

需要说明的是，图4 中的每条飞行轨迹分为3 段，其中第1、3 段在图中用虚线表示，中间第2 段用实线表示。第1 段为尚未发现禁飞区时以中末交班点为目标点的飞行轨迹；当飞行器与禁飞区中心点的距离小于禁飞区半径的2.5 倍时，认为飞行器探测到前方的禁飞区，开始绕飞，即用实线表示的第2 段绕飞轨迹；当飞行器与中末交班点距离，小于禁飞区中心点与中末交班点距离时，认为禁飞区绕飞结束，进入虚线表示的第3 段飞行轨迹。在训练时截取第2 段禁飞区绕飞的样本数据训练倾侧角智能制导模型。

3.2 倾侧角智能制导模型的训练

将840 条训练飞行轨迹数据输入图3 基于LSTM 的禁飞区绕飞倾侧角制导模型中，基于监督学习的思想，选取均方根误差（Root Mean Square Error，RMSE）作为评价指标，其定义为

式中：N表示轨迹的数目；R表示每一条轨迹的样本点数。

训练结果如图5 所示，可以看出，均方根误差随着训练迭代次数的增加逐渐减小且趋于收敛。

图5 均方根误差随迭代次数的变化曲线Fig.5 RMSE-epoch variation curve

4 基于强化学习的禁飞区绕飞倾侧角制导模型的训练

在第3 节基于监督学习的禁飞区绕飞倾侧角制导模型训练的基础上，进一步将强化学习技术应用于禁飞区绕飞制导中，在禁飞区约束、中末交班点约束和硬约束条件下通过飞行器与环境进行大量交互，在“试错”的过程中设置有效的奖励（反馈），并利用PPO 算法训练倾侧角制导模型，进一步提升对不确定禁飞区的适应性。

基于强化学习研究飞行器禁飞区绕飞制导律，需首先利用马尔科夫决策过程对禁飞区绕飞制导问题进行建模，主要包括3 部分：禁飞区绕飞时的状态空间、绕飞决策的动作空间和绕飞奖励的设计。

1）禁飞区绕飞时的状态空间

飞行器的状态空间如式（5）所示，即s(t)=[Δr，ΔV，ψ，Ltogo，ψMCV，ψTCZ]T。

2）禁飞区绕飞时的动作空间

飞行器的动作空间A为倾侧角σ，包括倾侧角的幅值和符号：

3）禁飞区绕飞时的奖励设计

奖励根据任务需求进行设计，以引导飞行器在对禁飞区绕飞的同时，具备良好的能量和交班管理。奖励的设计包括过程奖励和终端奖励。除了终端奖励，设计过程奖励的目的是避免出现稀疏奖励问题，稀疏奖励容易使训练难以收敛。

4.1 过程奖励

过程奖励分为2 部分：

1）利用传统的预测校正制导引导禁飞区绕飞时的策略搜索，即强化学习算法的“利用”（Ex‐ploit）性质；同时需增加飞行器与环境交互过程中的探索性，期望其能够探索出比传统制导方法更优、适应范围更广的智能制导方法，即强化学习算法的“探索”（Explore）性质。该奖励定义为

式中：kcomd>0 为常数；σtra为当前状态下预测校正制导给出的倾侧角指令；σt为智能制导模型探索出的倾侧角指令。通过设计有效的Δσ域，以提供飞行器倾侧角指令合理的探索空间。

2）在绕飞过程中需要引导飞行器持续飞向中末交班点，该奖励定义为

式中：kgoto>0 为常数；dexit为判定禁飞区绕飞结束时的条件距离；dt为当前剩余航程，飞行器越接近绕飞结束点，该项奖励越大。

4.2 终端奖励

终端奖励分为2 部分：

1）负责对不合理情况进行当前局终止，并给出终局奖励ravoid。不合理情况的判断条件为

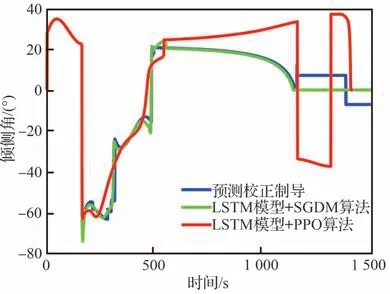
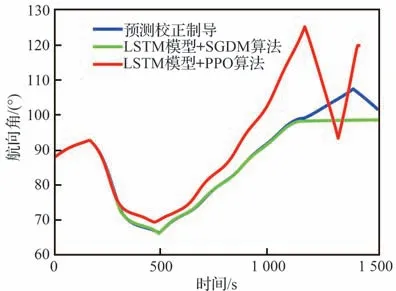
式中：cavoid为条件判断符，用于判断是否出现不合理情况，取布尔值0 或1，满足条件取1，触发结束当前局条件；Et表示飞行器的能量，其表达式为，EJB为中末交班点能量，Et

式中：aavoid>0 为常数。

2）飞行器精确到达中末交班点的奖励rJB，其定义为

5 仿真与分析

5.1 不同制导方法对比分析

以CAV-H 为研究对象，参数设置见3.1 节，比较3 种不同制导方法对禁飞区的绕飞效果：①预测校正制导方法；②第3 节基于监督学习中SGDM 算法训练禁飞区绕飞倾侧角制导模型的方法（图中记为“LSTM 模型+SGDM 算法”）；③第4 节中基于强化学习中PPO 算法训练禁飞区绕飞倾侧角制导模型的方法（记为“LSTM 模型+PPO 算法”），对比结果如图6～图10 所示。

图6 横向绕飞轨迹对比Fig.6 Comparison of horizontal trajectory for avoiding no-fly zone

图7 高度-速度对比Fig.7 Comparison of height-velocity

图8 倾侧角-时间对比Fig.8 Comparison of bank angle-time

图9 航迹角-时间对比Fig.9 Comparison of flight path angle-time

图10 航向角-时间对比Fig.10 Comparison of heading angle-time

由图6～图10 可以看出，“预测校正制导”与“LSTM 模型+SGDM 算法”2 种制导方式下的禁飞区绕飞的轨迹基本重合，这是由于利用监督学习训练倾侧角制导模型时，选取的禁飞区绕飞样本轨迹是基于预测校正制导方法产生，该训练过程可理解为对预测校正制导的拟合过程。由图6 可以看出，该方法虽然能成功绕飞禁飞区，但由于对禁飞区规避机动过大而导致能量损失过多，在绕飞后无法精确到达中末交班点。“LSTM模型+PPO 算法”制导下的绕飞轨迹明显不同于预测校正制导下的飞行轨迹，在过程奖励和终端奖励的引导下，探索出比传统制导方法更优的智能制导方法，不仅能够实现对禁飞区的成功绕飞，且在绕飞后精确到达中末交班点。

5.2 Monte Carlo 仿真分析

为验证“LSTM 模型+PPO 算法”制导方法的鲁棒性和对参数偏差的适应性，对飞行器再入初始状态、气动参数进行拉偏仿真分析。

在如表2 所示的再入初始状态扰动和气动偏差的条件下，基于“LSTM 模型+PPO 算法”制导方法进行729 组的Monte Carlo 仿真，落点经纬度的散布图如图11 所示，可以看出中末交班点的经纬度均匀分布在θf=50°、ϕf=0°周围，且最大落点偏差控制在±0.1°的范围内。

表2 飞行器再入初始状态和气动参数偏差Table 2 Initial state error and aerodynamic parameter perturbation

图11 初始状态和气动参数扰动下落点经纬度的散布图Fig.11 Scatter of longitude and latitude of setting point under initial state error and aerodynamic param‐eter perturbation

为进一步对比传统预测校正制导与“LSTM模型+PPO 算法”制导方法对禁飞区的绕飞效果，对比结果如图12 所示，每个格子代表不同的起始点经度、纬度、速度和高度，其中经度变化范围为[4.8°，5.2°]，纬度变化范围为[−0.2°，0.2°]，步长为0.05°；高度变化范围为[48，50] km；速度变化范围为[5 550，5 600] km/s。可以看出，在初始参数扰动情况下，“LSTM 模型+PPO 算法”制导方法相比于预测校正制导具有更高的绕飞成功率，其原因在于基于LSTM 的智能制导模型具有天然的泛化能力，因而对于参数的偏差具有更强的鲁棒性。

图12 预测校正制导与“LSTM 模型+PPO 算法”制导方法对比Fig.12 Comparison of predictor-corrector guidance and “LSTM model+PPO algorithm” guidance method

5.3 实时性分析

进一步分析“LSTM 模型+PPO 算法”制导方法在实时性方面的性能。在Monte Carlo 仿真中，基于“LSTM 模型+PPO 算法”制导方法完成一次禁飞区绕飞时倾侧角指令解算的平均时长为3.61 s，其具体分布如图13 所示，其中基于LSTM 模型生成倾侧角的时长为2.26 s，龙格库塔RK-4 积分时长为1.23 s。

图13 计算实时性对比分析Fig.13 Comparison of computing time analysis

与之对比，在Monte Carlo 仿真中，基于预测校正制导方法完成一次禁飞区绕飞时倾侧角指令解算的平均时长为18.49 s，其中纵向制导的平均时长为17.18 s，横向制导过程占其中的1.23 s。这是因为在纵向制导中，对动力学方程进行积分的预测过程和基于割线法求解倾侧角的校正过程计算量较大，占用的时间较长。而基于LSTM 模型的禁飞区绕飞倾侧角指令的解算没有“预测”环节和“积分”环节，大大减少了计算量，提高了计算速度。因而，在实时性方面，基于“LSTM 模型+PPO 算法”制导方法相比于传统预测校正制导具有明显的优势。

6 结论

针对传统基于优化类方法解决禁飞区绕飞存在计算量大、难以收敛的问题，基于预测校正的制导方法在纵向制导中仅以中末交班点信息校正倾侧角的幅值，未综合考虑禁飞区的位置信息和中末交班点信息，在横向制导中需要基于人工经验设计飞行走廊参数，对于突现的禁飞区适应能力差。利用强化学习技术在智能决策方面的天然优势，通过飞行器与环境大量交互“试错”，并借鉴人类基于反馈来调整学习策略的思想，基于有效的奖励（反馈）引导和强化学习中PPO 算法训练禁飞区绕飞倾侧角制导模型。该智能制导模型将倾侧角的幅值和符号一并输出，能够充分挖掘高升阻比飞行器强大的横向机动能力，以产生更优的绕飞策略。同时本文在绕飞时综合考虑禁飞区约束和再入终端约束，确保绕飞后具备足够的能量精确到达中末交班点。

尽管基于强化学习的智能制导技术能够充分挖掘飞行器的宽域飞行优势，且具备非线性映射能力和实时性方面的天然优势，但目前的智能制导技术存在难以回避的缺点：一是基于强化学习的智能制导技术本质上还是纯数据驱动的模式，需要飞行器与环境交互产生大量样本数据来训练神经网络模型，但在航天领域，真实的飞行数据往往难以获取，只能在仿真环境下获取，存在仿真环境与实际飞行环境不一致的问题；二是目前的人工智能仍然处于计算智能阶段，神经网络模型只能在训练样本数据集覆盖的范围内有效，依然不具备较强的泛化能力，实际飞行中若出现数据集范围外的情况，神经网络的性能将难以保证。智能制导技术与传统制导技术不是简单的替代关系，传统制导技术可以在关键点上吸纳人工智能技术在记忆、推理、拟合等方面的优势，2 种技术的交叉融合是飞行器制导控制的热门研究方向。