基于图优化的通信受限环境下协同导航方法

牛皓飞，蔡庆中，李健，杨功流

北京航空航天大学 仪器科学与光电工程学院，北京 100191

智能无人集群系统由无人机、无人车、机器人等多智能体通过彼此之间的信息交互构成，可以智能协同控制［1-2］，完成单个无人系统无法实现的复杂工作［3］，在军事和民用领域具有广阔应用前景。无人集群系统实现复杂的自主协同控制首要解决的一个问题便是节点间的时空统一问题，即系统中多智能体节点的相对与绝对定位与导航问题。

协同导航技术是一项在多智能体系统下提高个体定位与导航精度的关键技术［4-5］。在多智能体系统中，通过系统中各个子节点之间的导航状态共享与相互观测的方式来为子节点提供更丰富的观测信息，各个节点相互协同，可实现在低成本条件下的导航定位精度提升［6-7］，现有协同导航方法多采用Kalman 滤波实现［8-13］。

然而，在复杂遮挡环境下，节点与基站之间的通信会受到影响，无法保证观测信号的全覆盖。这需要系统具备处理观测信息时有时无、动态变化的能力，同时利用相邻协同节点的相对观测来对导航状态进行约束，实现复杂遮挡环境下的多无人平台协同导航。传统基于Kalman 滤波的协同导航方法观测方程状态维数固定，要求观测信息同时到达，无法解决遮挡环境下观测信号不同步、不连续的问题。而图优化算法将观测与状态约束编码为图模型中可增删的因子和顶点，具有很强的灵活性，目前已经在即插即用的多源组合导航系统中体现了优势［14-15］。因此，采用基于因子图模型的图优化算法在处理通信受限、观测信息动态变化的情况具有理论优势。

现有对图优化算法的导航应用研究中，主要集中在单个载体的多传感器融合领域［16-17］。目前对基于图优化算法的多智能体协同导航的研究仍然较少，文献［18］于2020 年提出了首个基于图优化算法的多无人机分布式协同导航方案，利用UWB 模块获得相对距离观测，与视觉惯性里程计的估计结果进行融合。文献［19］在文献［18］的基础上，通过在环境中放置1 个静态锚点，来纠正累计误差。其在导航状态估计过程中仅融合了视觉里程计与惯性信息，没有利用到UWB 观测信息对惯性器件进行校准，本质是一种松耦合，无法在通信受限情况保持精度。文献［20］于2022 年提出了基于激光雷达的分布式多无人机协同导航方案，并提供了基于图优化方法的精确估计结果，解决了文献［18］等基于视觉类方案受到视场环境局限的问题［21-23］，且不依赖于锚点。该方法为每个节点配备了高精度激光雷达导致了较高的成本，且激光雷达里程计和惯性导航都存在误差累积的问题，累计误差需要依靠回环检测来消除。综上，在视觉组合导航的相关应用中，图优化方法已取得较好效果。本文将重点关注其应用于惯性/里程计节点的协同导航，验证其在通信受限环境的全局优化效果。

基于以上研究成果，本文提出基于图优化算法的分布式协同导航方法，采用成本较低的UWB 测距信息提供相对导航约束，实现复杂环境下的高精度、高可靠协同导航。主要贡献如下：①面向室内、丛林等复杂遮挡环境下无线电信号不稳定环境，采用图优化算法解决传统滤波方法无法适应观测信息不同步不连续的问题；② 针对无线电信号拒止环境下节点通信短时中断问题，通过建立惯性航位推算因子图约束模型，在图优化算法中对陀螺零偏等内参进行同步优化与实时补偿，提高个体短时间自主导航的精度保持能力；③针对复杂环境下，协同导航节点拓扑结构动态变化、锚点观测信号不足的问题，提出基于图优化的分布式协同算法，通过节点间的相对距离观测提高集群综合导航精度。

1 问题建模

在丛林、室内等复杂通信遮挡环境下，无线电信号会受到遮挡等因素导致通信中断。在此条件下智能体与锚点之间的非视距量测可由与附近协同节点之间的相对量测代替。一个典型的室内通信遮挡环境如图1 所示，无人集群系统主要由智能体节点以及室外数量有限的定位锚点构成，节点1 处于室外通信较好环境下，可接收到2 个锚点的信息；节点2 位置较差仅能接收到1 个锚点；节点3 环境最恶劣，接收不到任何锚点信息。

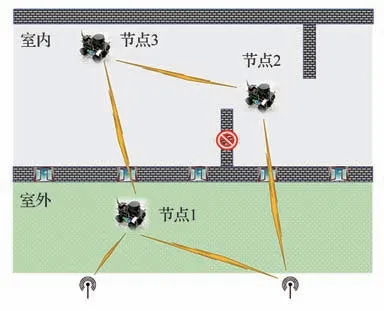
图1 系统结构图Fig.1 Model of system structure

通过节点间的协同与相互观测，可以有效为处于通信拒止环境下的节点提供丰富的观测信息，从而提高节点导航精度。由于在实际情况中，对高度的测量一般由特定的传感器获得，为简化运动学模型，不考虑高度项。根据不同传感器的原理，分别建立对应于图优化模型的约束形式，具体推导如下。

1.1 航位推算约束

对系统中单个智能体进行分析，由于智能体平台通常配有速度传感器，如无人车配备的里程计。因此利用航位推算在短时间内保持定位精度，导航定位的主要误差来源于陀螺漂移，基于此建立航位推算模型，如图2 所示。设陀螺零偏不随时间变化，智能体在k−1 时刻与k时刻之间的状态递推方程为

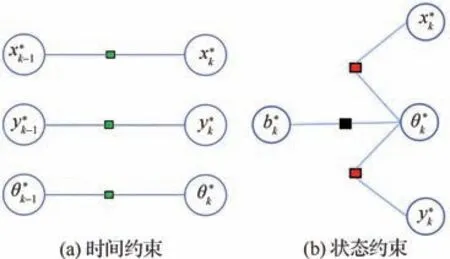
图2 航位推算因子图模型Fig.2 Dead reckoning factor graph

式中：ts为采样间隔；θk为智能体k时刻的航向角；θk−1为k−1 时刻的航向角；ωk−1为k−1 时刻天向陀螺仪输出的角速率；xk为智能体k时刻的x轴位置坐标；xk−1为k−1 时刻的x轴位置坐标；vk−1为里程计k−1 时刻提供的速率；yk为k时刻的y轴位置坐标；yk−1为k−1 时刻的y轴位置坐标；bk为k时刻的天向陀螺零偏。

根据2 时刻之间的状态增量构建残差约束，设待估计状态量为。以*代表该变量参与优化，其余作为已知量测值输入，不参与优化。根据约束的不同可以分为时间约束与状态约束，时间约束基于2 时刻之间状态增量建立；状态约束基于同一时刻下不同状态量之间满足的约束关系建立。

首先建立k−1～k时刻的时间约束，表示为

对残差进行求偏导，对应雅可比矩阵为

k时刻的状态约束可表示为

其中，天向陀螺零偏bk影响航向角的误差，以当前时刻航向角估计值与量测值建立残差：

根据式（1），展开θk：

设零偏为常值

则式（5）化简为

航向状态约束：

对应雅可比矩阵为

1.2 UWB 相对测距约束

基于UWB 提供的距离观测信息，建立UWB相对测距约束，约束形式可表示为

式中：dk为k时刻载体通过UWB 相对测距获得的与协同节点（或锚点）之间的距离观测值。坐标（xc，yc)为协同节点（或锚点）坐标值。对残差进行求偏导，对应雅可比矩阵为

基于上述建立的图模型中因子节点具体残差形式与雅可比矩阵，对因子图模型的架构进行定义。对于系统中任一协同节点，状态变量包括节点位置坐标、航向角、天向陀螺仪零偏。设为：Xk=[xk，yk，θk，bk]，对应因子图中的顶点。观测约束连接状态变量，对应因子图中的因子。根据不同传感器的模型建立不同的约束方程，对应图中与顶点相连的因子节点。建立系统中智能体导航定位的因子图模型如图3 所示。

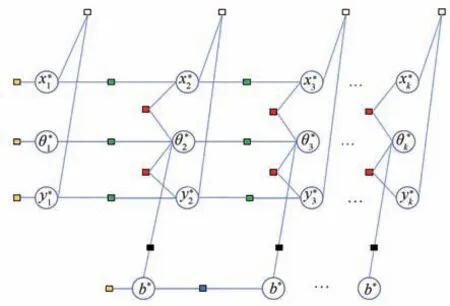
图3 智能体的因子图模型Fig.3 Factor graph model of agent

本节对系统中的传感器观测建立了因子图模型，为后续的非线性优化提供了框架。利用不同传感器的特性建立不同的约束。其中航位推算模型分别建立了时间约束和状态约束，利用IMU 和里程计无突变、随时间发散缓慢的特点，建立时间约束对UWB 的随机噪声起到了平滑作用。同时，利用状态变量之间满足的约束关系对节点航向与陀螺零偏进行了估计。所估计出的零偏将在后续算法中进行实时补偿，抑制导航误差的发散，使节点在无法接收到信号的环境中也能够保持一定的导航精度，该精度取决于零偏估计结果的精度。

2 算法设计

2.1 图优化算法设计

基于1.2 节建立的系统因子图模型，采用非线性优化算法对状态进行估计。系统图模型如图4 所示。

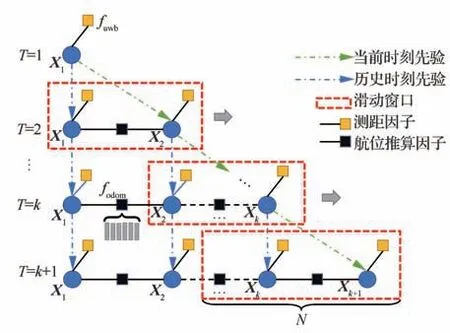
图4 系统因子图模型Fig.4 Factor graph model of system

算法流程步骤如下：

步骤1设定起始时刻各个状态变量的初值，添加先验因子到图模型中。

步骤2基于上一时刻优化结果进行航位推算，得到的下一时刻预测值作为优化初始值，添加到图的顶点。将历史时刻的优化结果，设为历史时刻状态的初值，添加到图的顶点。

步骤3添加UWB 测距因子与航位推算因子。将协同节点发送的相对观测信息作为UWB测距因子加入图模型。

步骤4根据所推导的目标函数与雅可比矩阵，采用LM 算法对图模型进行非线性优化，重复步骤2～步骤4。

设系统优化变量为所有时刻的状态变量，表示为

优化的目标函数是图模型所有残差平方和，设航位推算因子的2 种约束残差分别为

每个UWB 因子对应一组距离观测，将k个时刻的所有观测残差的平方进行累加得到总UWB因子残差，设k时刻载体共接收到m组UWB 观测，表示为

则系统优化目标函数为

图优化算法将各个观测量编码为因子图模型中可任意增删的因子，对应的数学表达式为式（16）中可随时加减的残差项。残差平方和的形式具有即插即用、可动态增删的特点，且图优化是包含历史时刻的全局优化，因此即使智能体节点在恶劣环境下仅能接收到一个锚点的观测信息，也能够与历史时刻的观测因子对状态构成约束。因此本文基于图优化的方法具备解决动态变化、复杂环境下锚点观测不足的问题。将所推导出来的各残差项的雅可比矩阵代入增量方程，推导出的雅可比矩阵用于指导图优化的方向，由增量方程求出单次迭代的状态最优估计值为

根据本文的系统与模型，构建信息矩阵的形式为

本文贡献主要来源于对3 种约束因子的设计与数学推导，在算法实现过程中采用Levenberg-Marquardt 这一通用优化算法对目标函数进行迭代求解。

2.2 协同导航算法设计

本节对本文协同导航架构与协同导航算法进一步阐述。在本文的多智能体协同导航系统中，UWB 基站作为固定锚点信息源，具有最高精度的坐标位置信息供其他智能体节点参考。但由于本身位置固定不动导致其通信范围有限，在协同定位系统中基站仅对智能体节点提供观测信息，不更新基站自身的位置坐标。因此智能体节点接收到基站的观测在图模型中是一种一元边。对此构建的信息传播因子图模型如图5 所示。图中，为t−1 时刻下的智能体节点1 的状态变量，为t时刻下的智能体节点1 的状态变量；为t时刻下的智能体节点1 与上一时刻构成的时间约束因子；为t时刻下的智能体节点1 与当前时刻状态量构成的状态约束因子；为t时刻下的智能体节点1 接收到的来自一个UWB 锚点的相对测距因子。

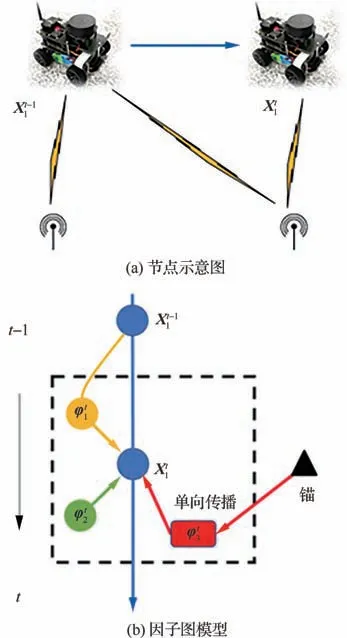
图5 无人车与基站协同导航模型Fig.5 Model for cooperative navigation of unmanned vehicle and base station

在协同终端为室外锚点的情况下，相对测距因子的数学形式为

式中：(xanchor，yanchor)为所接收到的UWB 基站在局部坐标系下的坐标。坐标系以左侧UWB 基站为原点，左侧基站指向右侧基站方向作为坐标系x轴，右侧基站的位置坐标由两基站之间所获得的相对距离观测信息取平均值得到。

在分布式协同导航系统中，智能体节点之间可以互相作为协同节点。以系统中任意2 个相互通信的智能体节点为例，将状态按照时间轴展开，构造协同导航算法的因子图模型如图6 所示。如图所示，为t−1 时刻下的智能体节点2 的状态变量，为t时刻下的智能体节点2 的状态变量；为智能体节点2 发送给智能体节点1 的自身位置信息与相对测距信息；为智能体节点1 发送给智能体节点2 的自身位置信息与相对测距信息；在t时刻智能体节点1、2 依靠航位推算分别进行自定位，将协同终端发送的位置信息与相对测距信息作为量测，将观测编码为因子加入自身因子图模型中，每个节点分布式地执行局部图优化算法。随后将优化结果进行广播发送给协同终端，协同终端利用此相对观测信息作为相对测距因子再进行优化。经过多轮迭代后，终端节点的位置精度会逐步提高。

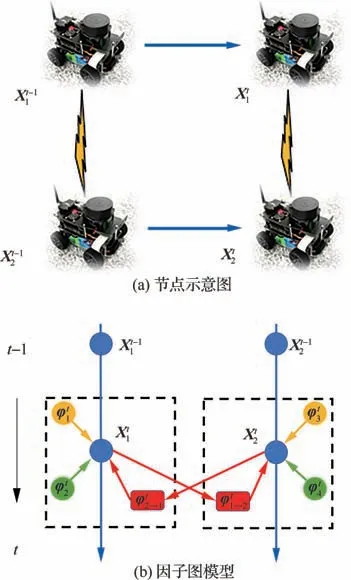
图6 无人车之间协同导航模型Fig.6 Model for cooperative navigation between un‐manned vehicles

在协同终端为其他智能体节点的情况下，相对测距因子的数学形式为

式中：(xcoop，ycoop)来自协同节点在当前时刻下通过自身观测信息进行位置校准后的定位结果。下面将分别设计典型场景对算法进行验证。

3 仿真与实验分析

为检验基于图优化算法的协同导航系统定位性能，设计典型场景进行仿真与实验分析研究。验证算法在锚节点有限、观测异步、动态增删复杂条件下的协同导航定位精度；验证算法处理异步、动态增删信息的能力；验证分布式协同导航算法对导航定位精度的提升。

3.1 仿真验证

如图7 所示，节点1 从室外进入到室内，室外可同时接收到2 个锚点的观测信息，室内由于墙壁遮挡，UWB 信号时有时无，节点1 能间歇接收到2 个锚点其中的一个观测。以3 辆无人车节点为例，节点1 靠近墙壁行进，部分UWB 观测信号可透过窗户到达无人车接收机，故节点1 接收信号条件较好，可作为高精度节点。节点2 距离锚点较远，但轨迹靠近门，可接收到一个锚节点的观测信息。节点3 的信号接收情况最差，既不靠近门也不靠近锚点，因此处于无锚点环境下。依靠节点之间的协同，节点2 可收到与节点1 之间的相对测距信息，节点3 可收到节点1 和节点2 的相对测距信息。期间设所接收到UWB 相对距离观测误差为0.1 m 白噪声。陀螺仪零偏设为200（°）/h，角速率随机游走；航位推算解算周期0.1 s，UWB 采样间隔1 s。仿真时间300 s，仿真结果如图8 所示。

图7 仿真场景Fig.7 Simulation scenarios

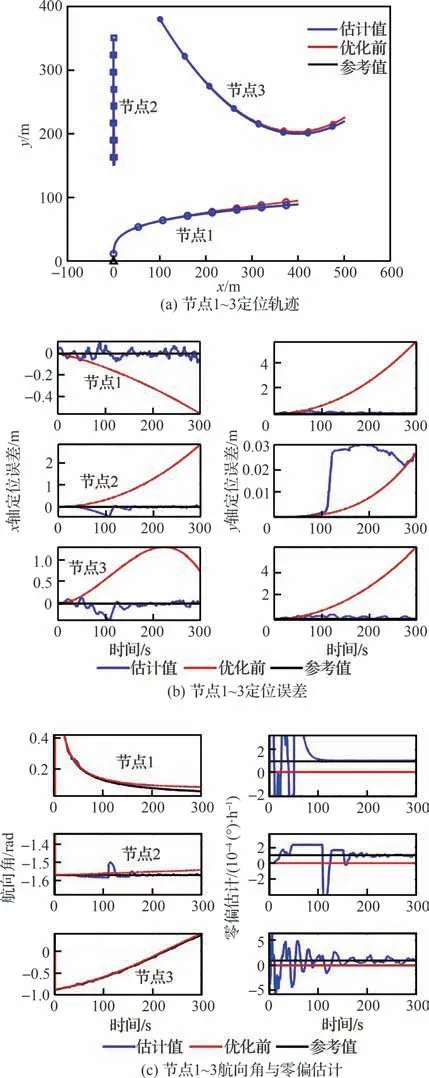
图8 仿真估计结果Fig.8 Simulation results

如图8 所示，节点1 靠近锚点一侧，保持水平直线运动。在0～50 s 期间可同时收到2 个锚点的观测信息。50～100 s 无法接收到锚点观测，100～300 s 通过窗户可间歇性交替接收到2 个锚点中的其中一个观测信息，处于观测信息不同步的环境下。

如图8（a）所示，锚点坐标分别位于坐标（0，0）m 与（400，0）m 处，3 个节点导航定位误差均得到了有效校准。节点1 在观测信息时有时无、不同步的情况下仍能保持较高导航定位精度，节点2 在仅接收到一个锚点观测情况下，利用节点1 相对观测信息能够有效抑制误差发散。节点3 在没有接收到锚节点观测的情况下，通过与节点1、2 的协同，最终导航定位精度高于航位推算精度，有效抑制了导航误差发散。节点3 在全程没有接收到锚节点观测的条件下，依靠与节点1 和2 的协同，同样实现了位置误差校正。

如图8（b）所示，从上到下每一行分别是每个节点的x、y轴定位误差曲线，节点1 在观测信息时有时无且不同步的情况下，仍能保持定位误差<0.2 m。在100 s 时刻后，节点1 进入了室内，节点2 与节点3 接收到了来自节点1 的相对观测信息，3 节点间的协同对各个节点的状态产生了约束作用，因此3 个节点在该时刻的状态量均有较小程度的跳变，其中节点2 的x轴误差有效降低，y轴误差受相对观测影响有小幅度增大，但总定位误差仍然降低。节点2 与节点3 由于不能收到2 个锚点的观测，定位精度低于节点1，但通过与移动节点的协同，保持定位误差不发散，相比于单纯航位推算，导航定位精度获得了较大的提升。

如图8（c）所示，从上到下每一行分别是每个节点的航向角、陀螺仪零偏估计曲线。3 个节点的航向角均收敛至了真值附近。其中节点1 依靠2 个锚点有效估计出了陀螺仪零偏，估计结果1.040 0×10−3rad/s，真值为9.691 4×10−4rad/s，误差<10%。节点1 在50～100 s 的无锚点期间，通过零偏的补偿，航位推算没有产生明显的发散，导航精度得到了有效提高。节点2 和节点3由于无法获得2 个锚点的观测信息，零偏估计误差较大，但也能够收敛至真值附近上下波动。

节点1 在观测信息时有时无、不同步的情况下仍能保持较高导航定位精度，验证了所提出算法的即插即用性，使系统能够处理观测信息时有时无、信息异步的问题，具备比卡尔曼滤波更强的灵活性。在通过节点之间的协同获得了高于单个节点航位推算的导航定位精度，验证了协同导航算法的有效性。

节点4 在400～600 s 期间处于通信最恶劣的无锚点观测环境下，仅在0～200 s 期间通过室外接收锚点观测估计出的零偏进行补偿，抑制导航误差的发散。在长时间恶劣环境下进行导航，误差呈线性发散，发散程度取决于零偏估计的精度，由于处于室外时间较短，零偏估计与真值之间存在一定误差，但综合定位精度高于航位推算方法，证明了本文方法的有效性。

3.2 综合模拟实验

实物系统如图9 所示，包括3 辆同配置无人车作为系统节点以及4 个UWB 基站作为系统锚点。在实验场地上沿路径设置共25 组地标点，在每个地标点上静态放置定位节点60 s，采集放置期间产生的4 个锚点网络定位数据，对得到的定位结果取平均值抑制随机误差的影响，将得到的基准点坐标作为定位基准。

图9 系统节点单元Fig.9 A platform in system

无人车节点仅采集室外2 个锚点的观测数据，室内锚点仅用于提供基准。实验过程中，同时控制3 辆无人车按照各自的路线行进，与此同时每个节点分别记录行进过程中所产生的所有传感器数据。将采集的数据经同步处理后进行离线解算。

实验场景如图10 所示，东西两侧各有一扇可进出的大门，经实测在门口附近可收到门外的一个锚点观测信息，行进至室内中间路段，观测迅速减少至无法接收到任何锚点观测。在两门之间以及东侧门右侧所有区域均无法收到任何一个室外锚点的观测，为完全无锚点观测的拒止环境，节点仅在室外以及正对门的区域能够收到观测信息。

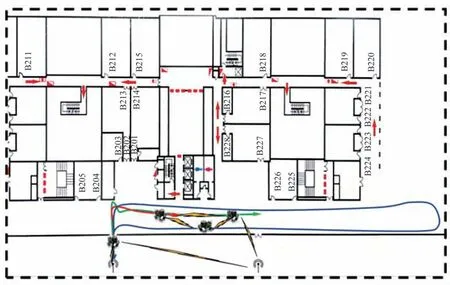
图10 实验场景分布示意图Fig.10 Scene map of the experiment

3 个无人车节点按照先后顺序依次从室外开入室内，节点1 最早进入室内，并沿着图10 中蓝色轨迹行驶，经过东侧大门后继续向东侧无锚点区域行进，到达距东侧门60 m 的东侧区域后掉头返回至西侧大门，为3 个节点中行进距离最远的节点。节点2 在节点1 到达室内最东侧即将掉头时开始行进，节点3 滞后节点2 约20 s 从门口附近开入室内。在行进过程中3 辆无人车按照各自的路线行进，彼此之间通过UWB 模块保持通信。节点1 在掉头后，节点2 从西侧大门进入室内，此时节点1 能够接收到来自节点2 的相对观测。在节点2 行进至东侧大门附近时，节点3 从西侧大门进入室内，此时节点2 可接收到来自节点3 的相对观测，节点1 可同时接收到来自节点2、3 的相对观测。

对各个节点的观测变化情况进行分析，全程节点1 由在室外收到2 个锚点观测，到进入室内后观测减少至0，再到掉头后与节点2、3 的协同，观测数从0 增加至2 个，处于观测信息动态变化的情况。节点2 进入室内后所收到的观测信息逐渐由室外的2 个锚点减小到1 个，在进入室内后向东侧形式观测数减少至0，在无锚点环境中收到了掉头后来自节点1 的相对观测，最后到达东侧门口接收到室外的1 个锚点观测以及来自节点1 的相对观测，观测数恢复至2 个。节点3 最晚进入室内，仅行驶至西侧门口附近为节点1 和节点2提供相对观测信息。

按照上述条件采集各个传感器产生的原始数据，进行离线解算，全程时长300 s。系统所采用的器件参数如下：UWB 测距模块采用NOOPLOOP 的LinkTrackP-B 模块，测距随机误差10 cm，频率50 Hz；无人车航位推算解算频率50 Hz，IMU 型号为MPU9250，RMS 噪声0.1（°）/s。基于采集的实验数据进行离线解算的结果如图11 所示。

图11 实验结果Fig.11 Experiment result

由实验结果可见，本文提出的图优化算法可以提高各协同节点的定位精度，尤其对于通信环境最恶劣、导航时间最长的节点1 最为明显，如图11（a）和图11（b）所示。全程无人车基于航位推算方法的定位均方根误差为3.96 m，采用图优化方法不对零偏进行补偿的情况下定位均方根误差为2.31 m，采用EKF 方法进行协同导航的定位均方根误差为1.67 m，采用图优化方法进行协同导航的定位均方根误差为1.52 m。采用本文提出的方法节点1 在长时间处于拒止环境下综合定位精度相比航位推算方法提高了61%；节点1大部分时间均处于无锚点环境，观测信号不连续情况占比较少，精度相比EKF 提高了9%，节点2受观测不同步的影响较大，定位精度相比EKF 方法提高了17%。节点3 处于可接收到2 个锚点观测区域内的时间较长且运动时间最短，与基于滤波的方法定位精度差异不明显；与航位推算方法相比，节点2 定位均方根误差由0.69 m 降低到0.32 m，节点3 由0.46 m 降低到0.27 m。

4 结论

本文针对复杂环境下通信受限的问题，提出了基于图优化算法的分布式协同导航方法。通过数学仿真与综合模拟实验，验证了所提出方法的有效性，结论如下：

1）针对复杂遮挡环境下锚点观测不同步不连续的问题，建立系统因子图模型，将观测与状态约束编码为图模型中可增删的因子和顶点，使得系统具备处理异步、动态增删观测信息的能力。数学仿真结果表明，该方法在锚点观测不连续不同步情况下，相比于连续同步观测的导航定位精度无明显变化。证明了该方法在复杂环境条件下的灵活性和适应性。

2）针对无线电信号拒止环境下节点通信短时中断问题，利用所建立的包含惯性航位推算的因子图约束图优化模型实现陀螺零偏的实时估计，在无锚点环境内通过对零偏的补偿有效降低了航位推算误差的累积。仿真结果表明，所建立的模型可精确估计出陀螺零偏，估计误差<10%。综合实验结果表明，该方法使得短时通信拒止环境下长期处于无锚点环境下的单节点定位精度相比航位推算方法精度提高了61%。

3）针对复杂环境下，协同导航节点拓扑结构动态变化、锚点观测信号不足的问题，利用节点间相对测距信息，设计并实现了分布式协同导航与定位算法。通过节点间的相互观测约束，有效抑制了复杂拒止环境下节点的导航误差发散，使集群在复杂通信受限环境的综合定位精度提升1 倍。

后续将进一步研究无锚点环境下的多无人平台协同导航问题，解决无锚点条件下分布式协同导航存在误差耦合、发散问题。