汽车排气管V形金属密封环设计与优化*
2023-07-28李卫民张凯璇杨瀚文刁家宇
李卫民 张凯璇 杨瀚文 刁家宇
(辽宁工业大学机械工程与自动化学院 辽宁锦州 121001)
密封件作为发动机排气系统中必不可少的组件,主要用于排气管各法兰间的密封连接,其密封性能直接影响发动机动力性能。研究表明,泄漏量减少1%,可使发动机动力增加1%,耗油率降低0.1%[1]。因此,提高发动机排气系统密封性能对提升发动机动力性能具有重要意义。
弹性金属自紧式密封技术作为满足现代高温、高压、高转速等复杂载荷条件提出的一种新型密封方式,目前广泛应用于航空航天等恶劣工作环境下的气路密封,金属密封环凭借其截面形状的多样性能够满足不同环境下的密封要求[2]。姜旸等人[3]针对航空发动机高温、高压、强震动环境中的W形金属密封环进行了研究,总结出回弹性能与静力学状态之间的变化规律。蒋发光等[4]对超高压大直径下使用的C形金属密封环适应性进行了研究。张文昌等[5]对核反应堆容器中的O形金属密封环进行了研究,讨论了表面镀层对密封性能的影响。黄发等人[6]针对发动机高压转子间密封连接所使用的U形金属密封环密封性能进行了研究,并对结构进行了优化。何东升等[7]对井下复杂环境中的V形金属密封环进行了研究,为流量控制阀中密封环设计提供了参考。上述对不同截面形状的金属密封环的研究,主要集中在航空航天、高压容器等环境中,密封环在这些领域中的使用与研究已经相对成熟,而在车用密封领域,密封环的设计使用与性能分析却较为缺乏。
本文作者基于自紧式金属密封环研究成果,考虑汽车排气系统的工作环境,设计一种适合汽车排气管密封的V形金属密封环,对其密封性能进行了分析,并对结构参数进行了优化。
1 V形密封环结构设计
1.1 密封环工作环境
密封环安装于汽车排气系统法兰盘之间,通过与法兰盘间的接触配合完成密封,如图1所示。
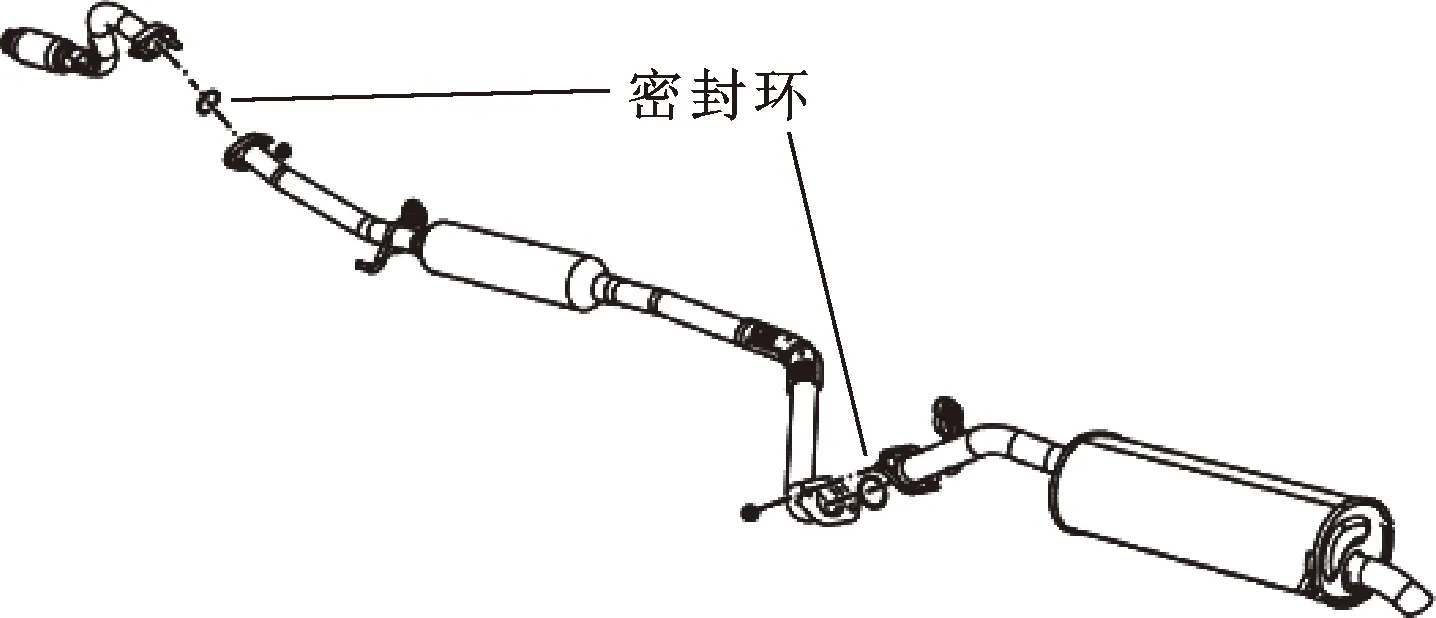
图1 汽车排气系统
安装时,对上法兰施加轴向压缩位移载荷,密封环依靠自身两侧的接触面分别与法兰盘紧密接触产生以接触压力,从而对气体介质形成密封。
工作时,密封环受到气体介质压力的作用,其自身的结构特点能使径向气体压力转变为轴向扩张压力,补偿接触面之间的密封压力从而达到自紧的效果[8]。密封环安装示意图如图2所示。
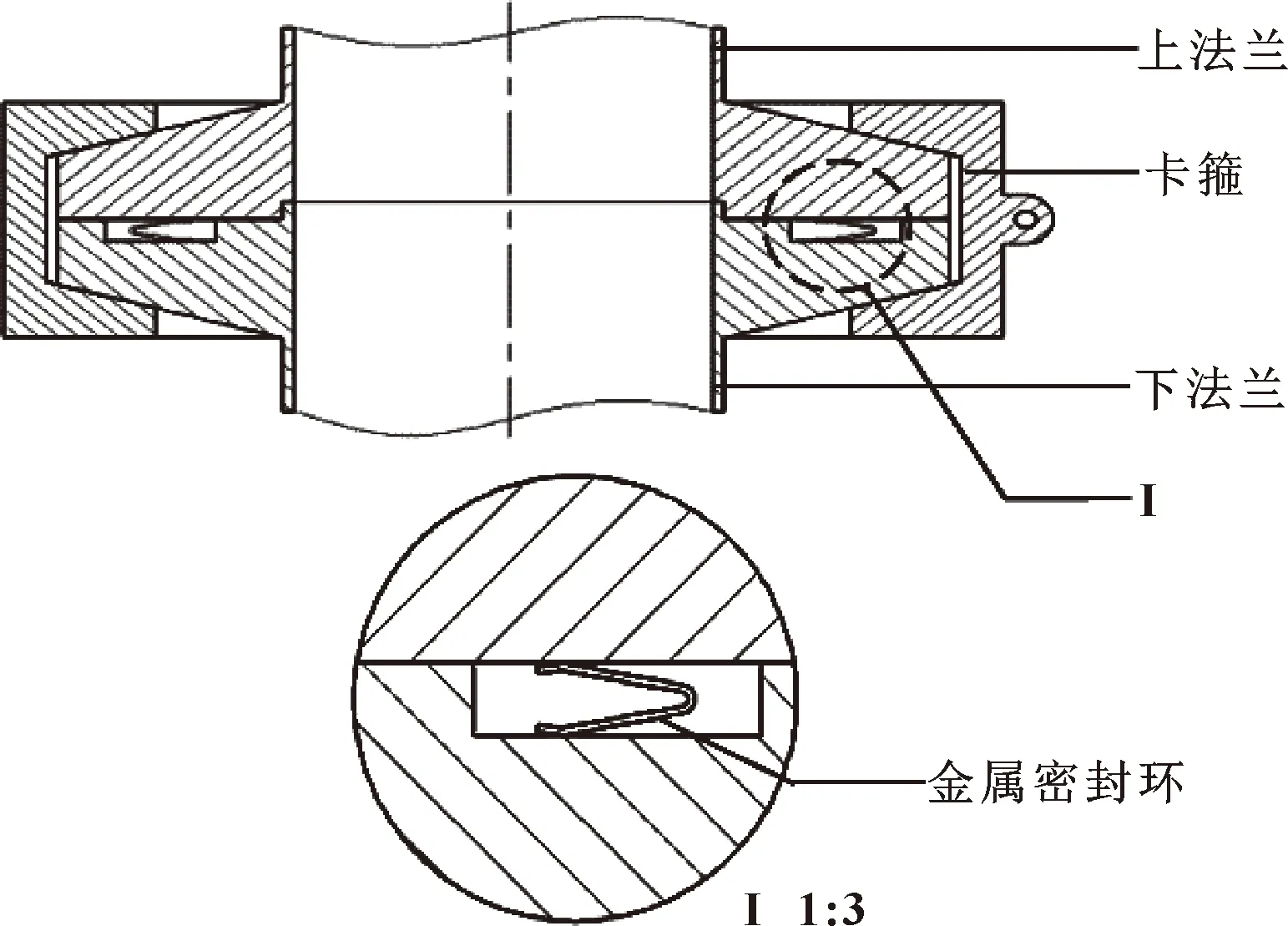
图2 密封环安装示意
1.2 密封环结构及材料
自紧式金属密封环具有耐高温、回弹量大的优点,目前常见的结构为O形、C形、W形、U形等[9],依据自身结构特点适用于不同的密封环境。为提高汽车排气管法兰盘之间的抗振和防松性,结合不同类型密封环的优缺点,提出了一种适合汽车排气系统密封的回弹量大、结构安全性高、轴向载荷要求低等特点的V形金属密封环。考虑排气管法兰尺寸与排气系统的工作要求,结合企业经验,设计的V形密封环结构如图3所示,结构参数如表1所示。

表1 V形密封环结构参数
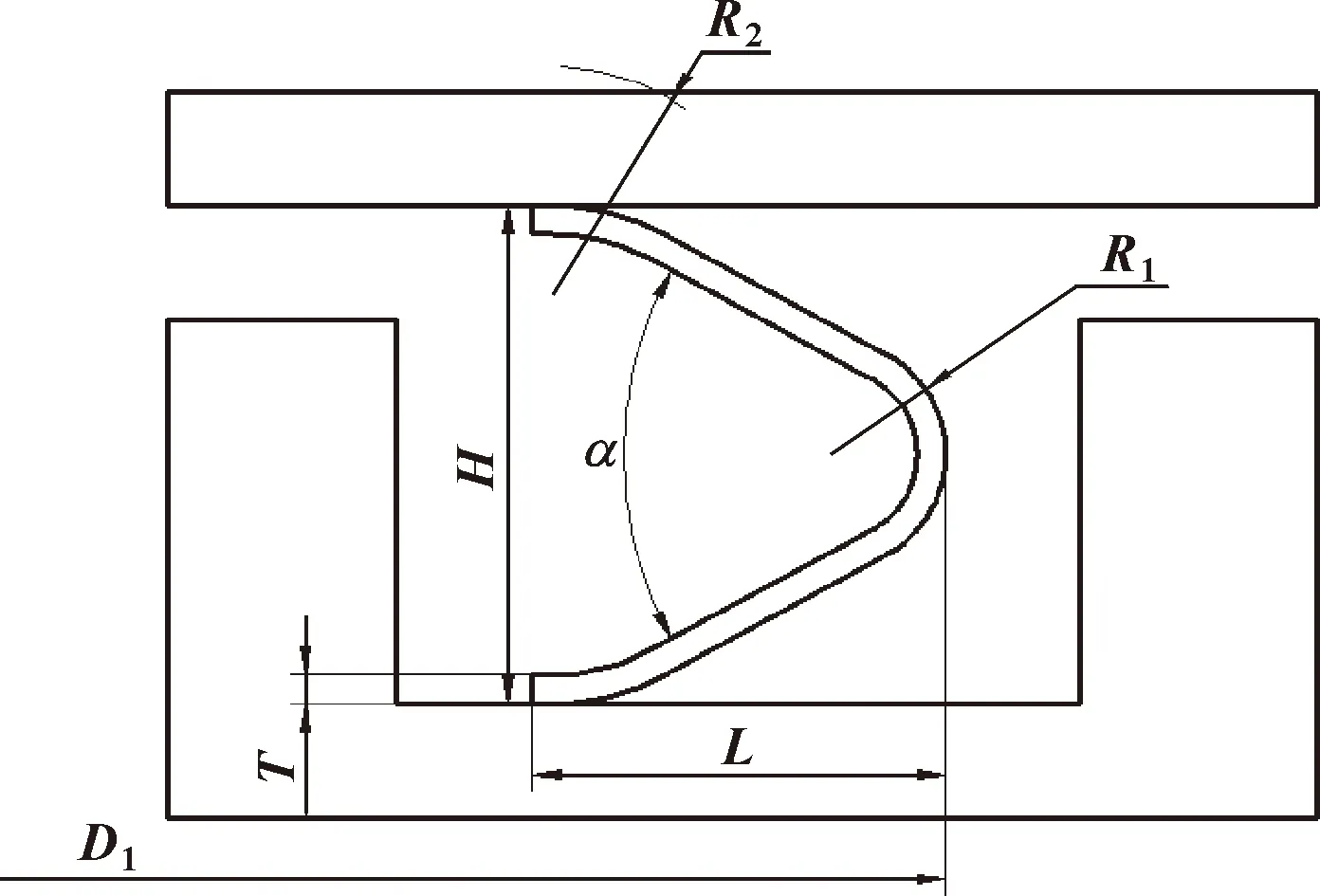
图3 V形密封环结构
相较于航空发动机的密封,汽车排气管密封环所需密封面压较小,因此将航空领域密封常用的线接触、大接触压力密封方式改为平面接触、小接触压力方式,既满足了密封要求,又避免了较大的预紧力;在波谷处采用圆弧过渡,降低了密封环的整体刚度,提高了其回弹性能;侧边倾斜一定角度以增大密封环的回弹性能。
汽车排气系统具有复杂载荷条件,受到高温与气体介质压力的作用,因此对材料性能提出了较高的要求。为了满足密封环密封强度,选择GH4169高温合金为V形密封环材料,该合金具有良好的加工性能,被广泛用于航空发动机密封领域,且年产量在高温合金中占比超45%。该合金部分材料性能如表2所示[10]。

表2 GH4169高温合金部分材料性能参数
2 V形环密封性能分析
密封件的密封性能主要是由接触压力、等效应力、回弹率表征的。通过对常温预紧及工作条件下压缩量对密封性能的影响分析,在保证2种工况密封强度下选择合理的轴向压缩量。
2.1 有限元模型建立
V形密封环为轴对称结构,为了确保分析的准确性和减少分析量,采用UG软件建立V形环的二维实体模型,并导入ANSYS Workbench中进行有限元分析。对二维实体模型进行网格划分,设置与上下法兰间的接触为摩擦接触,摩擦因数为0.15。有限元模型如图4所示。

图4 V形密封环有限元模型
密封环接触及边界条件如图5所示,施加的边界条件如表3所示。

表3 边界条件
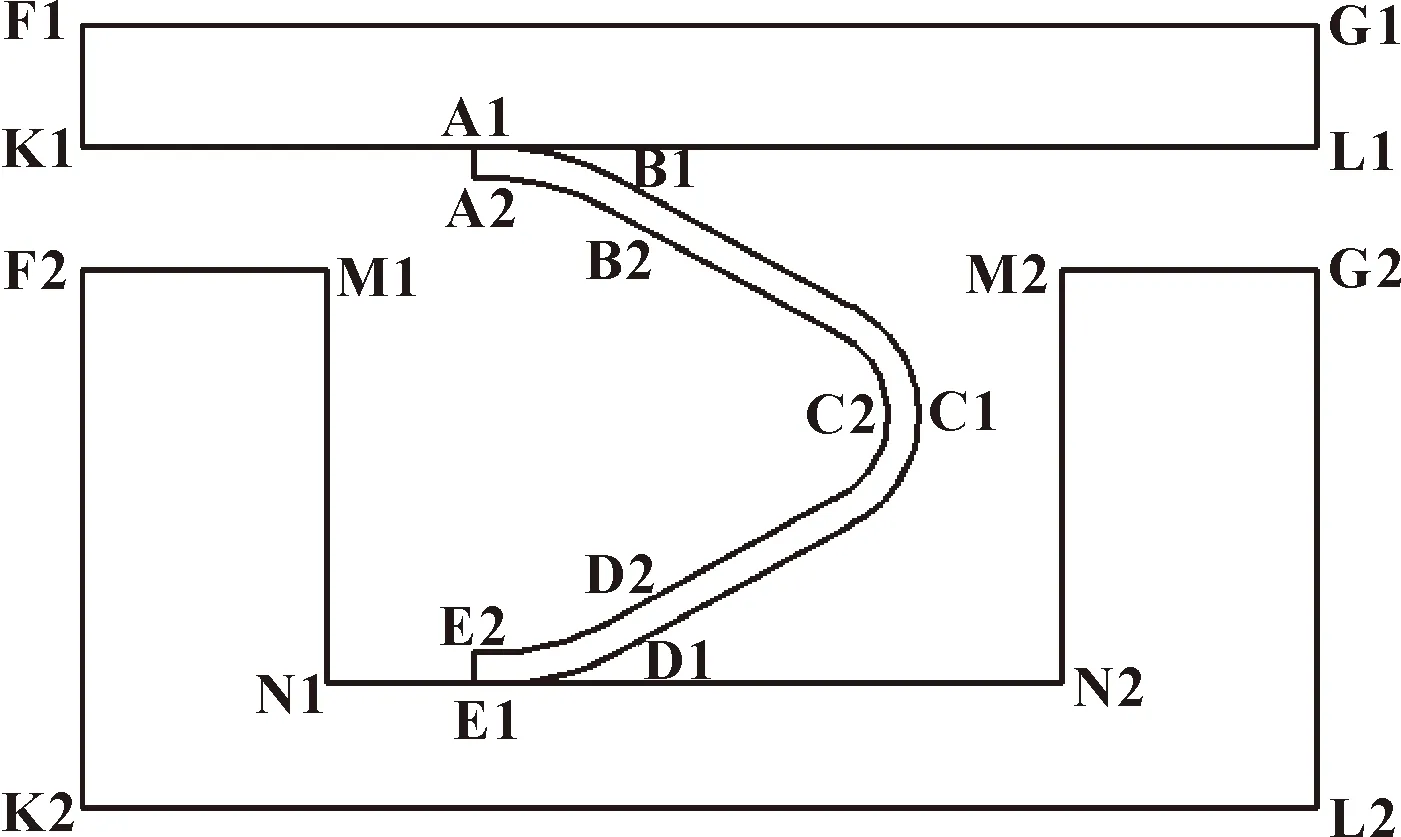
图5 V形密封环边界条件
该密封环适用于4.6 N系列柴油发动机,工作时,除了位移约束边界所受的轴向约束外,同时对压力边界施加0.45 MPa的气体介质压力,热边界施加600 ℃温度载荷。
2.2 常温预紧状态密封性能分析
密封环安装时,在常温下只受到上法兰盘的位移约束载荷作用,密封特性与最大等效应力与接触压力相关。初步设计时,参考GB150《压力容器》[11]中波纹金属垫片的密封要求及企业经验,最小预紧面压应大于17.5 MPa,屈服强度1 170 MPa。在常温条件下不同压缩量与最大等效应力关系如图6所示。
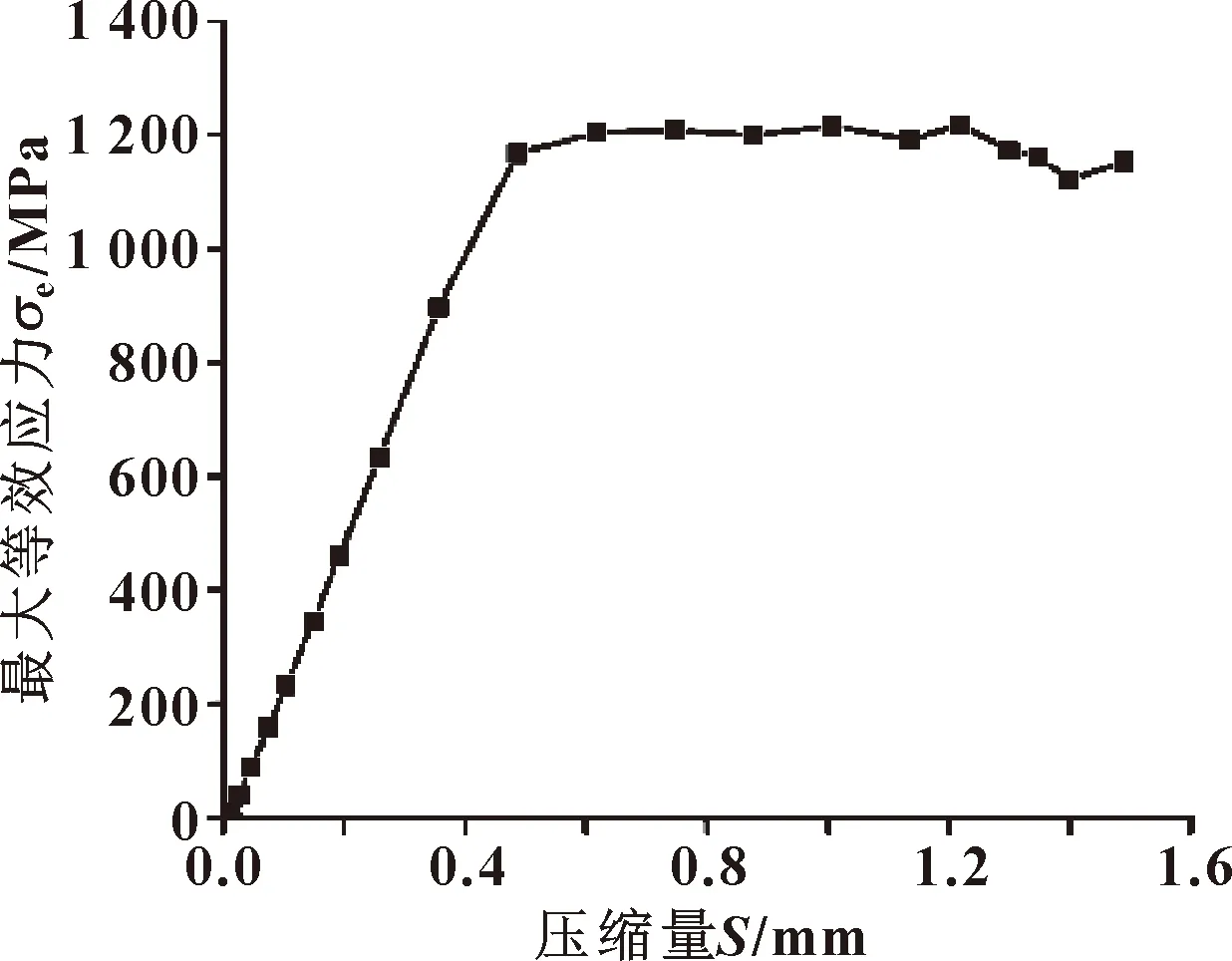
图6 常温预紧下最大等效应力与压缩量关系
可以看出:常温预紧下,压缩量在0~0.5 mm时,密封环最大等效应力随压缩量的增大而增大;在压缩量达到0.5 mm时,密封环最大等效应力达到其屈服极限,塑性变形区域主要集中在密封环波谷;压缩量在0.6~1.6 mm时,密封环达到屈服极限后最大等效应力基本保持恒定不再继续升高。
常温预紧条件下接触压力、接触宽度与轴向压缩量之间的关系如图7(a)所示。可以看出:随着压缩量的增加,密封环接触压力整体呈上升趋势,压缩量在0.9 mm时获得最大的接触压力。

图7 常温预紧下压缩量对接触状态的影响
通过分析图7(b)所示的接触压力分布可以看出,由于密封环自身的结构原因,在受到法兰盘压缩时,其密封环腿部发生翘起现象,在压缩量为0.9 mm时,此时密封环与法兰间的接触宽度最小,接触压力明显升高。不同压缩率下密封环与法兰接触部位的变化如图8所示。

图8 不同压缩率下V形密封环接触部位图
由图8可以看出,随着轴向压缩载荷不断增加,密封环接触部位与接触宽度不断发生改变,压缩量的选择上应尽量避免密封环宽度最小处,以增大接触面积,获得较好的密封性能[12]。
2.3 高温工况密封性能分析
工作状态下,要满足密封要求,其接触压力应满足σp≥mpc,其中pc为工作时的气体介质压力,m为密封环的垫片系数,参考GB150《压力容器》,m=6,计算得到工作状态下密封环接触压力应大于2.7 MPa,材料的屈服强度为976 MPa。对上法兰施加不同的轴向压缩量,得到压缩量与最大等效应力、最大接触压力的关系如图9所示。

图9 高温条件下压缩量与最大等效应力、最大接触压力关系
可以看出:在工况条件下密封环的整体最大等效应力小于常温预紧条件下,密封环最大等效应力随密封环压缩量的增加近似呈线性增大,最大等效应力仍出现在密封环波谷处。在研究的压缩范围内,密封环属于弹性变形阶段,未达到屈服极限,接触压力整体呈上升趋势,与常温条件下相似。其结构原因导致在压缩量0.9 mm时,接触压力显著提高,该处接触面积较小,接触压力较大。当压缩量在0.2~1.4 mm范围时,V形密封环即可满足密封强度要求。
2.4 密封环压缩率分析
压缩率是指对密封环施加轴向压缩载荷时,密封环变形量与初始环高的比值,压缩率需满足密封环压缩后具有良好的回弹性、密封环所受应力尽量小于材料的屈服强度、接触压力要满足工作时的密封面压要求。合理的压缩率是保证良好密封性能的前提。通过压缩回弹试验机,得到密封环压缩率与线载荷及回弹量关系曲线如图10所示。

图10 压缩率与载荷、回弹量之间的关系
由图10可以看出,当压缩率小于35%左右时,回弹量随压缩率提高而增大,之后回弹速率趋于平缓,压缩率大于35%时回弹量明显减小,主要是随着密封环波谷处屈服面积增大导致回弹性能降低,所以实际密封环压缩率的选择最好小于35%。对于常温预紧和高温工作下法兰间的密封,10%压缩率即可满足2种情况下密封面压要求,为了避免接触宽度的最小处,同时结合上文对常温预紧和高温工况下压缩量与密封性能分析,选择压缩率在25%~35%范围内可以保证密封环在常温和工作2种工况下的密封强度要求,密封性能和回弹达到较好的状态[13]。
3 V形密封环结构优化
上文分析可知,初步设计的密封环结构在合适压缩量下已满足密封要求,为了进一步降低等效应力,提高接触压力,减少密封环质量以降低材料成本,对高温工况下密封环结构参数对密封环性能及质量的影响进行分析,从而多目标优化筛选了设计变量。根据上文密封环压缩率分析,选择1.35 mm(压缩率30%)作为预紧安装时的轴向压缩量。
3.1 结构参数对密封性能影响分析
3.1.1 壁厚T
图11所示为壁厚与密封环密封性能的关系曲线。

图11 最大等效应力、最大接触压力与壁厚关系
由图11可以看出,随着密封环厚度的增大,其最大等效应力与最大接触压力逐渐增大,主要是因为壁厚增加使得密封环整体刚度增大。然而,在密封环壁厚的选择上并非越大越好,因壁厚过大会导致安装困难、易屈服等问题。因此在保证密封环有足够的刚度以满足密封压力要求的前提下,合理选择密封环壁厚。
3.1.2 环宽L
图12所示为环宽与密封性能的关系曲线。可以看出,随着密封环环宽的增大,最大等效应力和最大接触压力都逐渐降低。环宽的增加使密封环与法兰盘接触部位到波谷应力集中处的距离增大,最大等效应力随之降低,同时接触宽度的增大导致最大接触压力减小。

图12 最大等效应力、最大接触压力与环宽关系
3.1.3 开口角度α
图13所示为开口角度与密封性能的关系曲线。可以看出,最大等效应力几乎不随密封环开口角度的变化而变化,而最大接触压力随着开口角度的增大而逐渐减小。主要是因为在其他结构参数不变的情况下,开口角度的增大导致密封环与法兰间的接触宽度变大,密封环最大接触压力随之减小。

图13 最大等效应力、最大接触压力与开口角度关系
3.1.4 波谷半径R1
图14所示为波谷半径与密封性能的关系曲线。可以看出,最大等效应力随着半径增大总体上呈上升趋势,但变化幅度较小,其所受波谷半径的影响较小,而最大接触压力随着波谷半径的增大呈线性增长趋势。
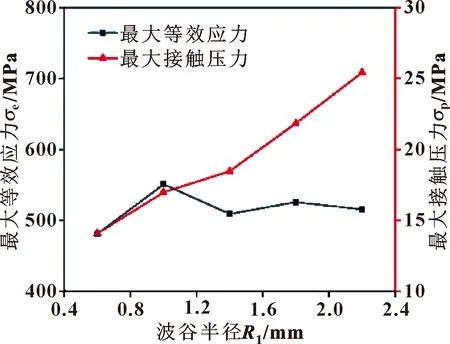
图14 最大等效应力、最大接触压力与波谷半径关系
3.1.5 接触圆半径R2
图15所示为接触圆半径与密封性能的关系曲线。可以看出,随着接触圆半径的不断增大,最大等效应力先增大后减小,但整体上变化幅度不大,可见接触圆半径对最大等效应力影响较小;最大接触压力随着接触圆半经增大而降低,半径增大使得密封环与法兰间接触更平缓,接触宽度增大,接触压力便减小。

图15 最大等效应力、最大接触压力与接触圆半径关系
由密封环结构参数对密封性能影响分析可知,壁厚、环宽、波谷半径、接触圆半径、开口角度均对密封环密封性能有较大影响。
3.2 结构参数对质量影响分析
取结构参数初始值的±15%,通过建立三维的参数化模型,分析各结构参数变化对密封质量的影响。由于壁厚的增加对质量的影响是显而易见的,同时又考虑到密封环材料板材生产规格的影响,因此文中不将壁厚这一参数作为分析与优化的对象。
图16所示为密封环结构参数与质量关系。可知,对密封环质量影响较大的结构参数有环宽、波谷半径、开口角度。

图16 密封环结构参数与质量关系
3.3 多目标优化
3.3.1 取值范围与约束条件
综上所述,对V形密封环密封性能及质量影响较大的参数包括环宽L、波谷半径R1、接触圆半径R2、开口角度α,选其作为设计变量,考虑密封环结构强度与配合法兰盘尺寸,设计变量的取值范围如表4所示。

表4 设计变量取值范围
建立多目标数学模型如下:
obj:min[σvon,m]
max[σp]
σvon≤976

3.3.2 DOE试验设计
通过Box-Behnken正交试验确定合理的试验设计点,以较少的试验数据获得高质量的响应面模型。部分正交试验设计点如表5所示。

表5 部分正交试验数据
3.3.3 响应面建立
根据正交试验样本点与响应值,建立各响应面近似模型,部分因素相互效应的3D响应面图如图17所示。

图17 部分响应曲面
对响应面模型进行精度检验,结果如表6所示。可以看出,响应面近似模型对试验样本具有很高的拟合度[14]。
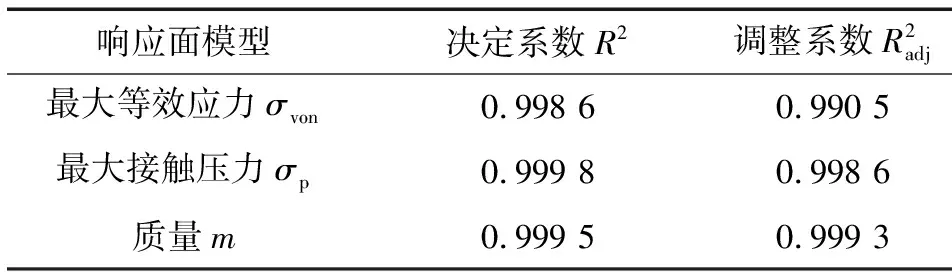
表6 响应面近似模型决定系数
3.3.4 结构参数优化
运用Design-Expert中Optimization模块[15],基于遗传优化算法,以min[σvon,m],max[σp]为目标得到优化后的密封环结构参数与初始参数对比如表7所示。

表7 优化前后密封环结构参数
初始密封环性能与优化后密封环性能对比如表8所示。

表8 优化前后密封环密封性能与密封环质量
优化后,密封环工作时最大等效应力减小了1.2%,最大接触压力增大了14.9%,质量减少了3.1%。
4 实验验证
将初步设计的V形密封环进行预紧安装,根据上文对压缩率分析,取轴向压缩量1.35 mm。通过面压试验机测量常温预紧下密封环与法兰间的接触压力。通过FUJI PRESCALE感印纸测量得到的密封环接触面压力如图18(a)所示,读取数据后的接触压力值如图18(b)所示。运用ANSYS Workbench软件对常温下面压实验进行模拟,得到仿真结果如图18(c)所示。实验与仿真结果吻合较好,满足密封环常温预紧下的密封压力要求,验证了密封环有限元模型的正确性和分析的合理性[16]。
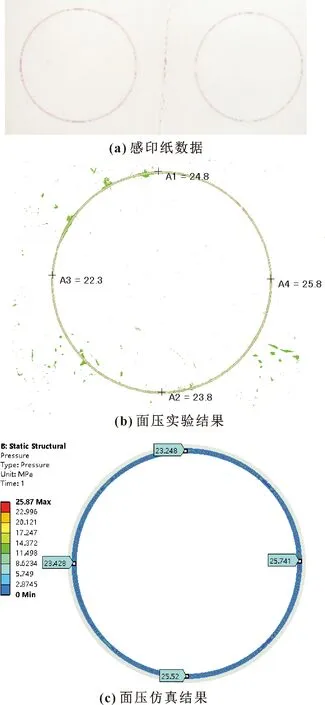
图18 感印纸与接触压力结果
5 结论
(1)根据汽车排气管密封环的工作环境和不同密封件的优缺点,设计一种V形金属密封环,并分析常温预紧安装与高温工况下轴向压缩量对其密封性能的影响,表明当密封环压缩率在25%~35%范围时可以保证常温和工作2种工况下的密封强度要求,密封性能和回弹都达到较好的状态。
(2)通过分析密封环结构对密封性能的影响程度:环宽L、波谷半径R1、接触圆半径R2、开口角度α对密封性能影响较大。
(3)以环宽、波谷半径、接触圆半径、开口角度为设计变量,以降低最大等效应力、提高接触压力、减小质量为目标,对密封环结构参数进行了多目标优化,优化后密封环工作时最大等效应力减小了6.4 MPa,接触压力增大了14.9%,质量减少了3.1%。
(4)通过对常温预紧下的密封环进行面压试验结果与仿真结果,验证了有限元模型的可靠性。
