表面微织构的组合设计及其对油封性能的影响*

2023-07-28张付英张志祥夏靖炜刘元刚

润滑与密封 2023年7期

张付英张志祥夏靖炜马骏刘元刚

(1.天津科技大学机械工程学院天津 300222；2.天津市轻工与食品工程机械装备集成设计与在线监控重点实验室天津 300222；3.天津市科技发展服务中心天津 300000)

为防止润滑油泄漏以及外界污染物进入设备内部，唇形油封被广泛应用于设备外伸转轴的密封。随着人们对机械设备密封和润滑性能要求的不断提高，表面织构技术由于能在相对运动的平行表面之间的流体中产生流体动压[1]，改善机械零件间的摩擦性能，因而得到广泛重视。OTTO和PATERSON[2]最先在旋转油封中应用表面织构技术，但由于缺乏微织构加工技术，该研究并未进行试验验证。STEPHENS等[3]利用X射线与紫外线光刻技术实现了对表面微织构的加工。ETSION和HALPERIN[4]、ETSION[5]将激光微表面纹理技术应用在机械密封中，研究其密封性能。HADINATA和STEPHENS[6]应用数值分析方法研究了微织构对唇形密封的弹性流体动力学效应。SHINKARENKO等[7]研究了表面织构对软弹性流体动力润滑摩擦学性能的影响，发现在刚性表面或软弹性体上施加球形凹坑形式的织构时，织构面积密度与纵横比等参数的选择，可以影响液膜承载能力。ROSENKRANZ等[8]将数值分析与实验相结合，对比研究了具有点状、凹坑、十字状、线状表面织构油封与普通油封的密封性能，结果表明，几种形式的织构都能减小接触面间的摩擦扭矩。国内学者对表面微织构也进行了大量的理论实验和研究。历建全和朱华[9]介绍了表面织构的图案和加工方法以及摩擦学性能的测试方法阐述了不同表面织构对摩擦学性能的影响及机制。王立辉等[10]研究了激光加工微织构对丁腈橡胶水润滑性能的影响，结果证明了橡胶表面加工的微凹坑织构有一定的减阻效果。董慧芳等[11]揭示了轴表面的微织构可以改善接触面之间的摩擦，有效地提高润滑性能。孔亚彬[12]对表面织构化的旋转轴密封性能与摩擦性能进行了研究，发现微织构的形状、大小、孔隙深度、孔隙方向和面积比对油封的润滑性能有很大影响。张付英等[13]研究了三角形、圆形和正方形微织构在考虑温度与否的2种情况下对油封密封性能的影响，发现不考虑温度影响时三角形纹理更有利于油封润滑性能和泵吸率的改善，而考虑温度影响时正方形纹理更有利。

本文作者在文献[13]研究的基础上，将3种形状的微织构进行组合设计，研究不同组合型织构对油封密封性能的影响。文中首先以油封唇口不同形状表面微织构为研究对象，建立了油封的有限元模型，分析了油封唇口接触压力的分布，然后建立了具有组合型微织构的密封表面间质量守恒雷诺控制方程，研究了相同条件下组合形状织构与单一形状织构以及无织构对油封表面密封性能的影响，并探讨了其润滑机制。

1 油封表面微织构的组合设计

1.1 油封的结构

油封的密封系统由3个主要部件组成：轴、密封圈和润滑剂，如图 1所示。以唇尖作为分割点，右侧为油液侧，左侧为空气侧。文中以某变速器输入轴外伸端轴承的密封油封为研究对象，该油封具有防尘唇、金属骨架及紧固弹簧，规格为60 mm×80 mm×8 mm，油封主体橡胶材料选用丁腈橡胶材料(NBR)，过盈量为0.3 mm，油侧唇角为45°，空气侧唇角为25°。

图1 油封密封系统示意

1.2 微织构的组合设计

大部分油封的表面微织构采用十字状、线状、三角形、正方形、圆形等单一几何形状。由于不同几何形状对油封的泵吸率、膜厚等影响程度存在差异，因此将不同形状织构进行组合设计，可综合2种不同织构的优点，从而提高密封的润滑特性和密封特性。

文中在前期等边三角形、正方形和圆形表面微织构对油封密封性能影响研究的基础上[13]，将三角形、圆形和正方形3种形状的微织构进行相互组合设计，得到如图2所示3种新的组合型表面微织构。

图2 组合表面织构示意

1.3 油封表面微观组合织构的设计参数

新设计的组合型微凹织构，均匀地分布在唇端两侧，如图3所示为组合型织构的分布。织构参数设计是以面积相近为原则，考虑到制造精度以及经济性，对于仅0.29 mm的接触宽度，数十微米范围的纹理比例是合理的，其具体参数见表1。

表1 织构参数单位：μm

图3 油封唇部微织构分布

2 油封的分析和计算模型

2.1 油封的有限元模型

为获得油封静态接触压力及径向变形影响系数矩阵，建立了油封有限元模型。在不影响分析结果又方便求解的前提下，对油封的有限元建模做出如下假设：

(1)旋转轴与油封骨架为刚性材料；

(2)油封为轴对称模型且其运行过程保持静止；

(3)模型运行期间，温度、黏弹性、材料密度随时间而产生的变化不做考虑，认为其为常数。

油封材料及建模参数如表2所示。丁腈橡胶的应力应变等性能是通过二项参数的Mooney-Rivlin模型来描述，Mooney-Rivlin模型中常数C10=0.994 MPa，C01=0.236 MPa[14-15]。有限元模型在划分网格时，骨架、旋转轴以及紧固弹簧采用C3D8R，油封则采用C3D10M来划分，织构区域单独拆分出来对网格细化，以保证计算精度及结果的准确性，如图4和图5所示。

表2 数值计算基本参数

图4 油封有限元模型

图5 油封唇口织构局部图

2.2 油封的数值计算模型

在密封唇与轴面之间会形成流体膜，流体膜不仅润滑了密封唇的界面，减少了密封唇的摩擦磨损，而且还通过流体动力作用支撑密封唇表面。文中采用雷诺方程来求解动压力分布，由于油膜厚度与旋转轴直径相比非常小，因此采用笛卡尔坐标系，x轴为周向，y轴为轴向，z轴为径向。在笛卡尔坐标系下，雷诺方程如式(1)所示。

式中：h为油膜厚度；p为流体压力；μ为流体黏度；φx与φy分别为x与y方向上的压力流量因子；φs为剪切流量因子，其取值参考文献[16]；σ为油封唇表面均方根粗糙度值；v为周向速度。

对各参数进行量纲一化处理：

式中：Lx为周向单个织构周期宽度；Ly为轴向接触宽度；pa为环境压力。

雷诺方程式(1)仅用于计算全油膜润滑状态。为了同时考虑空化和非空化区域，采用了修正的雷诺方程：

式中：F为空化指数；通用变量Φ为P的代替；K=Lx/Ly；ζ为量纲一旋转轴线速度，ζ=μ0vLx/(σ2·pa)，μ0为润滑油初始黏度。

修正雷诺方程的边界条件为

油封油膜厚度可在利用有限元分析求得油封的径向变形后，通过影响系数法计算得到。文中把油封一个周期Lx×Ly面积区域分为100×100个节点，节点i处的油膜厚度如式(3)所示。

式中：Hw为纹理结构参数；Hs为静态油膜厚度；(I)ik为径向变形影响系数矩阵；Psc为静态接触压力；Pt为总压力，由式(4)求得。

Pt=Pc+Pavg

(4)

式中：Pc为粗糙峰接触压力，由式(5)求得；Pavg为平均流体压力。

其中，ζ是集成的虚拟变量。

求解雷诺方程得到压力分布，就可以应用式(6)计算出泵吸率Q。

摩擦扭矩M由式(7)计算得到。

Ff为摩擦力，由式(8)求得。

Ff=-∬τxdxdy

(8)

式中：τx为油封表面剪应力，由式(9)计算。

3 油封的数值计算结果分析

3.1 数值计算流程

油封的表面润滑模型数值计算是基于MATLAB编程运算，通过不断循环、迭代，求解得到误差范围内雷诺方程的近似解，数值计算流程如图6所示。

图6 数值计算流程

3.2 油封有限元分析结果

图7所示为通过有限元分析软件Abaqus仿真分析得到的不同织构油封静态接触压力分布。可以看出，油封与旋转轴轴向接触宽度Ly=0.29 mm，最大接触压力位于唇尖处为6.05 MPa。由于微织构为凹坑式设计，因此织构处的静态接触压力小于唇尖其他部位。

图7 不同织构油封的静态接触压力分布

图8—11所示分别为不考虑微织构、具有不同组合型微织构时，油封的径向变形影响系数矩阵。图12所示为面积、深度与组合织构参数相同的正三角形织构油封径向变形系数矩阵。以上矩阵是在Abaqus软件中将单周期内区域划分成100×100个节点，在油封唇口节点处依次施加单位节点力后，分析所有节点变形情况所得到的。显然，在织构边缘处其变形系数会增大。

图8 无织构时油封的径向变形影响系数矩阵

图9 具有织构A时油封径向变形影响系数矩阵

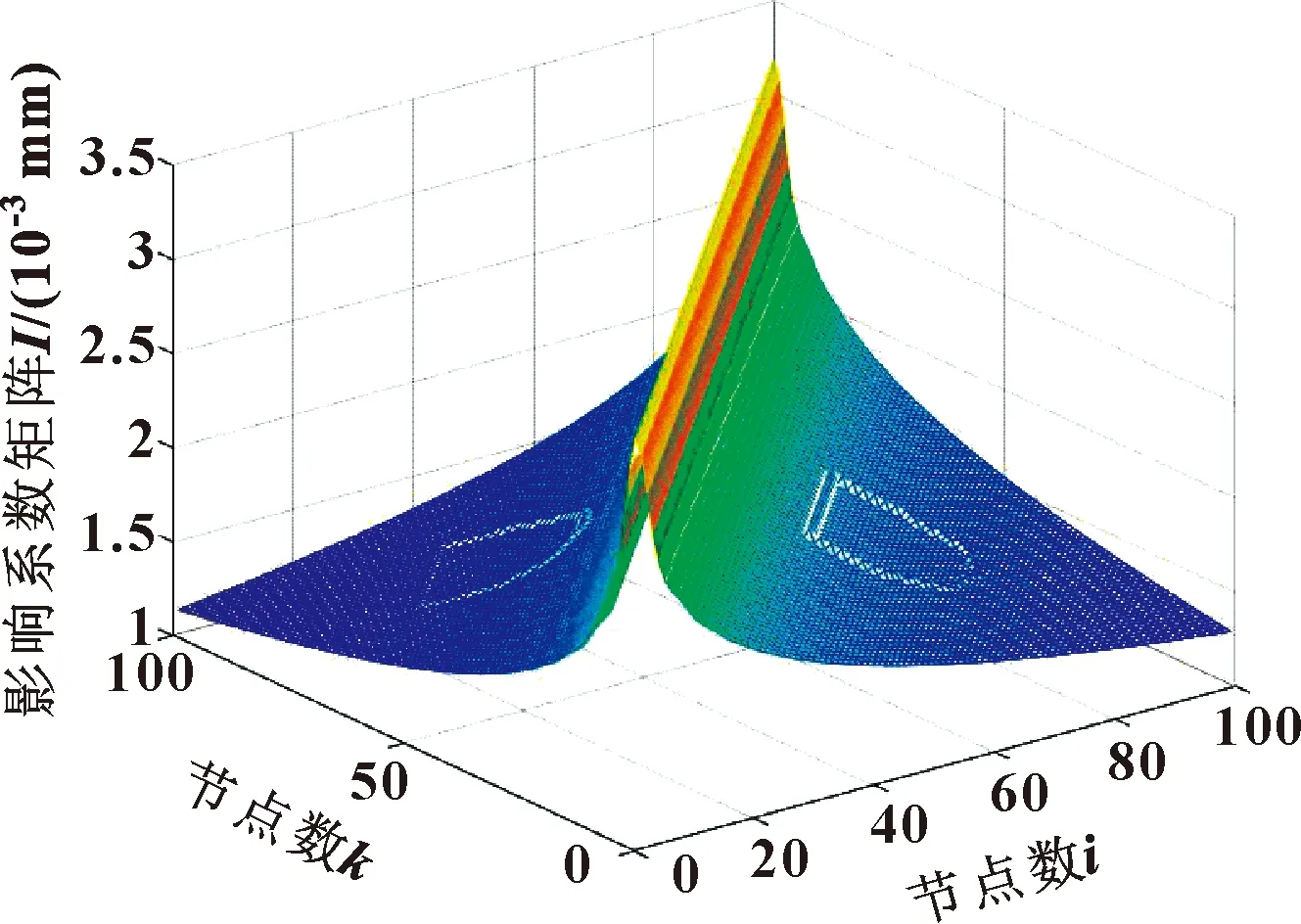
图11 具有织构C时油封径向变形影响系数矩阵

图12 具有三角形织构油封径向变形影响系数矩阵

3.3 油封的数值模型验证

为验证文中所建模型与结论的可靠性，将文献[17]具有三角形织构的模型参数代入文中模型中进行计算求解，并将油膜厚度与文献值对比，如表3所示。两者结果误差小于2%，验证了文中计算模型的可靠性。

表3 油膜厚度值对比

3.4 油封的数值计算结果及分析

图13所示为旋转轴转速为1 000 r/min时，不同织构唇形密封的动态压力在轴向位置的分布曲线。动态压力值是通过静态接触压力和粗糙峰接触压力与流体压力求差得到的。织构所在节点处，密封压力会出现波动，压力值较无织构区域稍大。这是由于微织构使节点处的最小膜厚极限值变大，降低了油膜压力，但增加了节点处的泵送率和膜厚，降低了粗糙峰压力。综合作用的结果，使微织构处的压力有所降低，但在2～99节点处密封压力一直大于0，表明油封一直处于混合润滑状态。

图13 不同织构油封唇口密封压力在轴向位置的分布情况

图14所示为旋转轴转速对具有不同形状微织构油封泵吸率的影响曲线。可见，泵吸率随转速增大而增大，且当转速大于1 400 r/min时，泵吸率增长幅度也大幅提升。这是由于当转速增大时，密封区域的流体动压效应会逐渐增强，导致泵吸率增加。具有表面织构的油封产生的泵吸率要大于无织构油封，且组合织构A与组合织构B对油封泵吸率的提升是优于三角形织构。这表明三角形和半圆形组合织构、三角形和正方形组合织构对油封泵吸率的提升无优于单一的三角形织构。且三角形与半圆形组合织构对油封泵吸率的提升效果最佳。

图15所示为旋转轴转速对具有不同形状微织构油封摩擦扭矩的影响。可见，摩擦扭矩是随着转速的提升而稳定增长。油封织构对摩擦扭矩影响极小，这是由于虽然微织构改善了润滑状态，但也增大了粗糙峰接触区域，最终使摩擦扭矩没有出现变化。

图15 旋转轴转速对不同织构油封摩擦扭矩的影响

图16所示为旋转轴转速对具有不同组合型微织构油封量纲一油膜厚度的影响。显然，油膜厚度随转速的增加而小幅递减，且有无微织构油封的量纲一油膜厚度均大于3，表明油封始终处于全油膜润滑状态。相同转速下，织构C对油膜厚度的影响最大，然后依次为织构B、织构A、三角形织构，且具有织构的油封油膜厚度明显大于无织构油封的油膜厚度，这是由于微织构更利于动压效应的形成所致。由于织构C的形状在相对运动方向满足从大口流向小口的条件，因此组合织构C(半圆形与方形组合织构)的油封动压效应更好。