初中数学二次函数应用题解题教学研究
2023-07-27苏春荣
苏春荣
【摘要】解题教学是数学教学的重要构成,数学教师需要关注解题教学的合理开展,并联系实际教学情况来构建解题教学策略,生成高效的教学环节.二次函数应用题是中考命题的要点,这一类题目具有较高的难度和综合性,对学生的信息获取能力和函数解题能力均有较高的考查要求.为了帮助学生突破二次函数应用题的解法学习,教师便可以从应用题的基本构成出发来设计教学.本文对初中数学二次函数应用题解题教学的开展作出研究.
【关键词】初中数学;二次函数;解题
解题教学是数学教师需要关注的内容,教师需要借助解题教学的开展帮助学生学习数学解题的方法,提升其解决数学问题的能力.应用题是数学题目中难度较高的一类题目,这一类题目的题干往往会提供一个现实的场景,学生不仅需要掌握相应的解题方法,还需要具有解析应用题、将应用题转化为数学计算题的能力.二次函数应用题是以二次函数知识考查为核心的应用题,这一类应用题是中考数学的考查重点,为了帮助学生突破二次函数应用题的解法学习,教师需要从实际解题规律出发做出设计.
1重视概念教学,打好解题基础
概念教学是应用题教学的基础.通过研究可以发现,应用题虽然与一般的题目存在解题方法上的差异,但应用题解题的本质也是概念知识的解题运用,二次函數的顶点式和零点计算是二次函数应用题的常用公式.若学生不能有效地掌握二次函数的概念知识,其在应用题解答中就难以合理地解析并设列算式.在当前,为了推动学生的二次函数应用题解法掌握,教师需要关注概念教学的开展,并在解题教学前利用基础习题的展示帮助学生回顾基础概念,为其打好解题基础.
例如在实际中,教师可以给学生展示如下习题,带领学生回顾二次函数的基础内容.
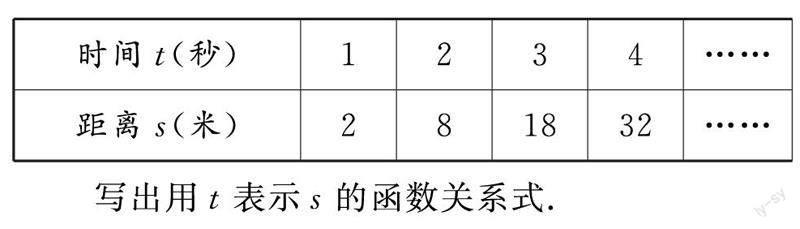
例1一个小球由静止开始从一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s(米)与时间t(秒)的数据如下表(s与t的关系可以视为符合二次函数关系):
例2抛物线y=-1/2x2的对称轴是_______,顶点坐标是_______,开口方向_______.当x_______时,y随x的增大而增大,当x_______时,y随x的增大而减小,当x=_______时,该函数有最_______值是_______;
在展示出两道例题后,教师便可以联系实际引领学生回顾,让学生思考已经学过的二次函数的相关概念内容,让其明确判定二次函数对称轴、顶点坐标、开口方向、零点坐标、函数上坐标的变化规律的具体途径.在完成这一基础习题的解析分析后,学生就可以对二次函数的基础知识生成较为深层次的认知,教师也可以趁势开展函数应用题的解析教学.
2关注读图审题,教授析题方法
应用题相较于一般的数学题目,其题干的构成较为复杂,学生需要通过阅读题干的方式来获取关键的解题信息,并剔除一些无关的干扰项目.为了帮助学生掌握二次函数应用题的解题方法,教师需要以审题读题为核心作出设计,选择典型的习题,教授学生有效审题的方法.如,在实际中,教师可以展示如下应用题作出诠释,让学生思考有效审题的方法.
例3某服装店购进一批服装,其中一种服装的进价为每件100元,售价为130元,每星期可以卖出80件,为了提高销量,商家决定降价促销,根据市场调研结果显示,该种服装每降价5元,每星期可以多卖出20件.求服装店原利润.在调价后,若想使收益最大化,该如何定价,此时最大利润又是多少?
在展示了该题目后,教师可以引领学生分析该题目的题干,让学生找出其中包含了题目有效信息的项目.学生通过研究易发现,题干中包含的有效信息为“服装的进价”“服装的售价”“当前每星期的服装销量”“服装每降价5元,每星期可以多卖出20件.”在学生完成这一审题后,教师便可以引领学生思考,通过这些信息你们可以了解到什么,这些信息又和习题的两个问题有何联系呢?学生在思考后可以得出“服装在降价后,销量会提升,相应的总利润也会提升,但单件服装的利润会降低,随着服装价格的降低,会出现一个价格,在这一价格服装的总利润最高”.在学生明确了这一内容后,教师就可以引导学生从两个题目入手做出条件的应用设计,让学生设列算式.通过这一过程,教师就可以带领学生经历应用题审题的有效过程,这对学生审题能力的发展是有利的.
3选择代表习题,解析题目要点
为了帮助学生系统地掌握二次函数应用题的特点与命题要点,教师在实际中需要选择具有代表性的二次函数应用题作出展示.在习题展示中,教师要结合应用题的题干和问题作出诠释,为学生解释不同的应用题提问方式所对应的考查内容,让学生可以通过题目的观察来明确题目的所求内容,进而设列二次函数式子.
例如在实际中,教师就可以联系具体的习题作出诠释,让学生认识常见的二次函数方程应用题类型,并让其认识习题的解题要点.在展示中,教师可以运用下述方式作出展示.
3.1利用待定系数法解答
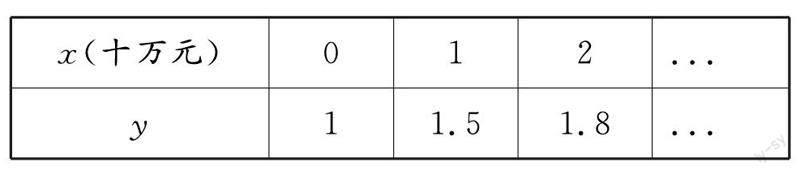
例4工厂车间生产的A型零件,其成本为2元,售价为3元,年销售量为100万件,为了提升工厂效益,工厂决定拿出部分资金定制广告.根据调研现实,每年投入广告费为x(10万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,其符合如下关系:
(1)求y与x的函数关系式.
(2)如果投入的年广告费为10万~30万元,请求出工厂年利润随广告费增大而提升的范围.
解析该类型题目考察点为待定系数法,题目中直接给出了y与x的二次函数关系,所以使用待定系数法可以直接求出y与x的函数关系,然后再结合二次函数的性质来求出(2)的所问内容.
3.2利润最大(小)值
例5某商场计划开展降价促销活动,其中参与打折的一款产品原售价为60元,每天可卖出50件.根据调查结果显示,在商品降价后,其销量会提升,符合如下规律:每降价1元每星期可以多卖20件,若商品的成本价格为40元,请问降价多少元可以获得最大利润.
解析该题目所考查的内容为利润最大值的求取,这一类题目的所求内容为二次函数的顶点,学生需要设列函数关系式,找出求取顶点的方法.
在实际中,学生需要了解几个概念,其分别为“单价”“商品利润”“价格变动量”“销售量变化”“商品总销售量”“总利润”“净利润”,针对这些概念,教师要作出实际解析,让学生了解其具体的内涵.
3.3二次函数构造
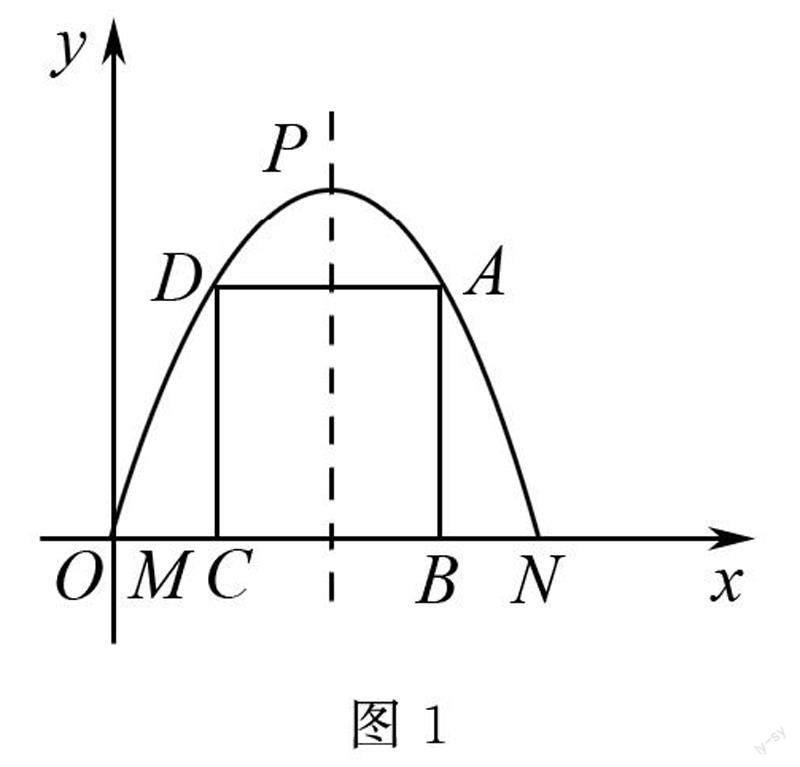
例6如图1,有一块拱形铁皮,其边缘呈现抛物线状,MN=4cm,抛物线顶点处到边MN的距离为4cm,若在铁皮上截下一矩形ABCD,使矩形的顶点B、C落在边MN上,A、D落在抛物线上,请问这样截得的矩形的周长能否等于8cm?
解析在这一题目中需要从抛物线来联系二次函数,然后根据题目所给条件来设列二次函数式.综合来看,这一类题目的考查要点是利用二次函数的图象、性质解决实际问题,具有较高的建模要求,学生需要结合实际的信息来构建二次函数模型,并创建直角坐标系,然后从二次函数与长方形的融合入手做出架构.
4构建变式练习,推动学生掌握
变式练习是一种具有较强针对性的练习设置,在变式练习中,教师可以通过一道典型应用题和其变式题来做出展示,让学生围绕习题的考查点变化来分别思考,进而帮助学生认识一类问题的有效解答策略.为了构建有效性较强的变式练习环节,教师需要做好课下资源的开发,通过教学检索与整合的方式选择代表性较强的习题作为变式练习的原式,然后再考虑题目的变形调整来生成一系列变式习题.
例如在实际中,教师可以使用如下的变式题构建变式练习.
原式某商品现在的售价为每件60元,每星期可卖出300件,市场调查显示:每涨价1元,每星期少卖10件;每降价1元,每星期可多卖20件,已知商品的进价为40元每件,如何调价才能获得最大利润?
变式1在原式的基础上,若商品原材料价格上涨,导致进价变为50元每件,此时如何调价才能获得最大利润?
变式2某商品进价为40元每件,现在的售价为每件60元,每星期可卖出300件,市场调查显示:每涨价1元,每星期少卖10件;每降價1元,每星期可多卖20件,若商场想要每星期获利6000元,且能符合降价促销的要求,应如何调价?
在展示了上述的原式和变式题后,教师便可以引领学生对三道习题做出分析,思考三道习题的区别,然后在完成三道习题的解答后,教师再引导学生分析利润求取这一类二次函数应用题的有效解答方法,促进学生完全掌握.
5立足“建模能力”,做出习题分析
“建模”是数学核心素养的构成部分,这一素养的培养对学生习题认知和解题能力的发展有着重要的意义.为了发展学生的“建模能力”,教师需要选择合适的习题作为对象进行研究,让学生在习题分析的过程中实现解题思路的具象化展现,进而形成解决一类题目的通用解题方法.在实际中,教师要为学生做出解题模型建立的方式展现,帮助学生加以认知和思考.
例如在实际中,教师便可以综合实际的二次函数习题做出“建模”的展示,让学生从解题模型的认知出发来获得“建模能力”的提升培养.其中,教师可以综合二次函数常见的利润最大(小)值求取问题做出展示.
这一类习题的解题过程可以做出以下模型规划:
(1)读题审题,获取关键信息;
(2)基于实际问题,整合题目条件;
(3)寻找函数关系,设列函数关系式;
(4)建立坐标系,分析函数顶点;
(5)联系题目要求,做出数据处理.
在用文字来阐述了这一类二次函数应用题解法后,教师便可以让学生结合具体的题目解题过程做出分析,将其中的共有内容剥离出来,总结这一类题目的通用解题思路,即通性通法.
6关注学生发展,优设解题评价
评价是教学的重要构成部分,有效评价设计可以点明学生存在的问题,进而推动其提升与发展.在二次函数应用题解题教学中,教师同样可以借助评价的进行分析学生的解题能力发展情况,再针对性地给出调整建议,以此推动学生的发展.
例如在二次函数应用题的基本教学告一段落后,教师可以开展专项测试,在其中为学生展现二次函数应用题.在学生完成应用题解答后,教师便可以联系学生的实际解题情况作出分析,找出学生易错题和出错原因.在此基础上,教师便可以展开解题评价,点明学生现阶段存在的主要问题,并给出调整的建议.其中,针对学生二次函数递增递减区间无法理清的问题,教师便可以给出评价“部分同学对二次函数的概念知识理解还是存在欠缺,二次函数的递增递减区间与其顶点有着密切的联系,请同学们再次回顾二次函数的基本内容来做出复习”.
7结语
总而言之,二次函数应用题解题教学的构建是教师需要关注的内容,教师要结合应用题的题目结构,从二次函数应用题的特征出发做出研究,让学生学习解答二次函数应用题的有效方法.在实际中,教师可以围绕概念教学开展、读图审题进行、题目要点解析、变式训练构建、习题建模开展、解题评价构建六方面来作出调整.
参考文献:
[1]黄林斌.初中数学函数应用题解题教学分析[J].高考,2018(29):195.
[2]邹迎春.初中数学函数应用题解题教学略谈[J].吉林教育,2017(39):47-48.
[3]程曦.初中数学函数应用题的解题对策研究[J].数理化解题研究,2022(08):44-46.
[4]张小亮.初中数学课堂教学中数形结合思想在函数解题中的应用探究[J].新课程(中),2019(01):37.
