混合陶瓷球轴承振动特性仿真分析
2023-07-27闫海鹏郎赛秦志英
闫海鹏,郎赛,秦志英
(河北科技大学机械工程学院,河北石家庄 050018)
0 前言
混合陶瓷球轴承具有噪声低、寿命长、能承受联合载荷等特点,其动态特性直接影响设备的运行与安全。为了及时发现早期轴承故障,有必要了解轴承的振动特性。轴承的运行工况较为复杂,导致滚动体与保持架、内外圈间时常产生碰撞和摩擦,从而引发各元件失效。由于这些问题影响轴承的正常运行,因此有必要建立一个能有效反映球轴承在运行中的振动特性的动态有限元模型。
国内外学者和专家对滚动轴承的动力学进行了大量研究,JONES[1]提出了套圈控制原理求解轴承动力学分析问题;TU等[2]提出了考虑打滑的滚动体与滚道面摩擦、接触力的圆柱滚子轴承振动响应动力学模型,证明了摩擦力会增大振动水平;LIU等[3]提出了考虑润滑和柔性环的轴承动力学模型,分析制造误差对高速柔性ACBB振动的影响;余光伟等[4]提出了具有3个轴承自由度的动态模型,结果表明套圈膨胀波数增加时,加速度响应也增大;刘静等人[5]根据赫兹弹性理论建立了时变冲击激励耦合的球轴承局部区域故障模型,阐明了其振动响应的规律;牟小燕等[6]通过建立套圈及滚道间的动载荷模型分析接触磨损,得出磨损频率在不同载荷分布下不会改变的规律;李震等人[7]提出了考虑离心力的轴承五自由度拟静力学模型,通过联合载荷对滚珠与内圈进行受力分析;葛伟伟等[8]建立了转子-轴承系统的数学模型,通过变刚度和加速度等分析其振动特性;黄伟迪[9]为了分析径向力和转速对滚动体与滚道面接触力的影响,建立了球轴承的拟静力模型;贺瑜飞[10]建立轴承接触特性和模态有限元模型,研究振动频率、振型变化等;边强等人[11]基于ABAQUS建立了轴承各元件的动态有限元模型,研究了径、轴向载荷和变速条件下保持架滑动速度的变化;李旭锋等[12]利用Workbench进行轴承接触特性与模态分析来获得运动性质。这些研究均取得了一定成果,并为改善轴承性能提供了依据,但很少涉及故障轴承有限元振动特性的研究。
鉴于此,本文作者以H7009C型轴承为研究对象,分析其在Workbench中正常与故障时的振动特性随载荷与转速的变化,利用球轴承进行应力、接触力以及加速度对振动特性的分析,进一步为其剥落故障检测提供依据。
1 角接触球轴承有限元模型
1.1 主要结构参数及材料参数
文中将H7009C型球轴承作为研究对象,其几何结构参数如表1所示。
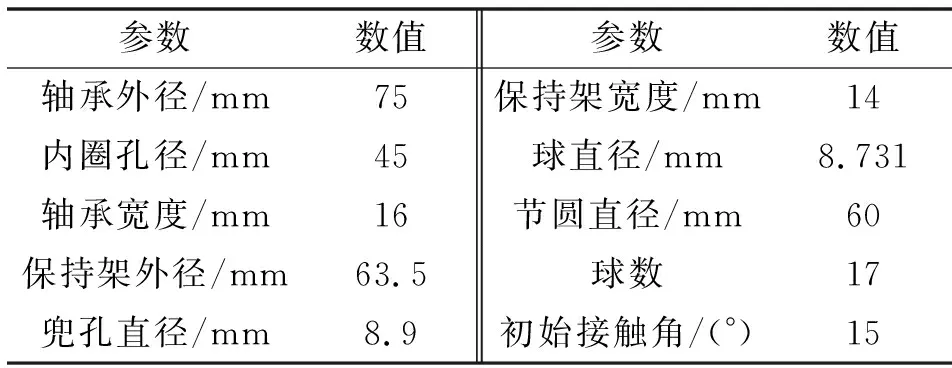
表1 H7009C角接触球轴承基本结构参数

表2 材料参数
1.2 网格划分和接触设置
通过Workbench软件中的Import Geometry功能导入轴承模型,此球轴承在运行时,滚动体、保持架、内外圈间的接触和运动间的关系非常复杂,因此直接由自身软件中的Mesh版块对滚动轴承三维模型划分网格。轴承几何结构存在较多曲面,一次性生成网格较为困难,故需先拆分轴承元件,再对模型生成网格命令。在网格划分过程中,利用扫略生成与Auto-Mesh划分两者混合的方式对模型进行网格生成。最终生成了轴承套圈表面的扫掠六面体网格,其他元件部分自动生成了四面体网格。对轴承套圈沟道与滚动体局部相接触的范围进行了网格细化完善。由于保持架存在兜孔,较为复杂,因此自动划分完成后再对其兜孔与滚动体接触面积处进行网格局部细化完善,以提高迭代接触精度。最终的滚动轴承网格模型如图1所示,共存在289 017个节点与173 326个单元。

图1 有限元模型
此轴承有限元模型建立了滚动体与套圈滚道的面与面接触类型,与兜孔间的面与面接触方式以及保持架凹面与内圈凸面间的面与面接触方式。需根据接触面法则正确选择主从面,其中主面包括内、外圈引导部分以及滚动体表面,从面包括内圈凸面与外圈凹面、轴承兜孔内面以及保持架凹、凸两面,共存在44对接触。接触中通过Pure Penalty函数设置计算模型,并同时调整Initial Information的参数应对接触的变化。根据角接触球轴承的工作特点,设置轴承滚动体分别与内圈、外圈沟道的摩擦因数为0.05,保持架与内圈凸表面、滚动体表面间的摩擦因数皆为0.1,调整各元件接触间的stiffness为每一步更新、Interface Treatment为自适应变换,通过滚动轴承各元件的材料与实际环境的考虑选择各接触区域的摩擦因数,以达到模拟实际工况的最真实情况。
1.3 边界条件和载荷的设置
根据轴承的实际环境状态,将轴承外表面添加全约束的固定方法,内圈则随轴运转,同时保持架与滚动体随内圈的转动而转动,共设置2个载荷步,每个载荷步又分为众多子步来分步计算,第一载荷步结束时间为0.05 s,第二步结束时间为0.12 s。在角接触球轴承的内圈设置joints,并对它设置转速,在第一载荷步结束时,转速达到最高且稳定转速,针对坐标系来约束x、y、z3个方向的平动,设置只绕z方向的转动,绕z轴的转速最高为4 000 r/min,径向施加固定载荷1 000 N,设置约束后的有限元模型与速度加载曲线分别如图2(a)与图2(b)所示。

图2 边界条件(a)和载荷(b)
2 仿真分析
2.1 正常与剥落轴承应力分析
模拟结束后,分别输出整个模型与各个轴承元件的应力分布云图,如图3、图4所示。图3是在1 000 N径向力下正常轴承的应力分布云图,结合内外圈与保持架等元件的应力云图分析得出:整体分析的下半部应力云图颜色较深,表明其应力值与接触面积较上部滚动体大很多。这一现象表明在动态状态下,轴承下半部滚动体承载高于上半部,表明角接触球轴承有较为明显的承载区与非承载区之分,并且应力分布主要集中在承载区和元件相互接触区域,符合现有的规律[13]。

图3 正常轴承整体应力云图

图4 各元件应力云图
从图4中可知:下部滚动体的接触面积和应力明显大于上部,滚动体载荷较大。产生此现象的原因可能是轴承径向力的作用直接施加在下部滚动体一侧,下面部分的滚动体与内外圈接触紧密,导致变形大,应力较大。从4组正常模型的分析结果及滚动体的应力分布云图得出:在正常工况且承受径向力作用下,模型的最大应力位于径向力方向最下方的滚动体上,此滚动体与外圈的接触位置靠近滚动体端部处。对比模型各元件的应力云图如图4所示,发现各元件应力大小顺序如分布云图所示,最大应力点位于滚动体上,滚动体平均应力最大,外圈次之,内圈和保持架应力相对较小些。滚动体端部会分别与滚动轴承保持架兜孔、内外圈沟道间产生冲击和摩擦,受力较为繁杂。
为了更直观地了解故障对轴承应力的影响,导出外圈剥落轴承整体与各元件应力大小分布云图如图5所示。

图5 剥落故障下轴承应力云图
由图5可以得出:最大应力发生在滚动体的受载区故障缺陷附近,并出现在滚动体端部与外圈的接触区域,和正常模型最大应力位置几乎一致。外圈故障下轴承的最大应力比正常轴承增大约42.2%,其中滚动体与内圈表现得最为明显,外圈与保持架没有太大变化,这表明剥落故障势必会给轴承带来极限应力的升高,故障越集中应力越大。原因是存在剥落的轴承构件结构和组织发生改变,当轴承元件转动到剥落位置时会产生较大冲击载荷,不断承受较大冲击载荷后,会出现疲劳损伤,严重时会使轴承发生破坏。
2.2 仿真信号的振动特征分析
通过比较正常轴承和剥落轴承的失效特征频率,导出外圈剥落模型的滚动体振动加速度信号,对采集信号进行FFT变换,加速度随时间变化的曲线就可以转换为频率谱,再通过接触力等变化即可发现故障的特征。当轴承存在剥落时,故障特征频率[14]分别为
(1)
式中:fo为外圈故障频率;fi为内圈故障频率;fb为滚动体故障频率;fc为保持架故障频率;fs为内圈的旋转频率;Z为滚动体数目。
卷积神经网络在目标检测上的成功应用,可以看作识别图像为目标还是为非目标。因此,本章设计了基于卷积神经网络的关键帧提取器,首先采用基于SIFT特征的关键点检测算法,在铁路视频图像上提取少量区域作为候选,并通过Alex-Net模型提取候选区域的深度特征,最后将特征输入到SVM分类器中进行分类,得到列车头部、尾部和车身三种结果,验证基于卷积神经网络的关键帧提取器的可行性。本文提出的关键帧提取器流程图如图3所示。
由于外圈剥落故障下,轴承的加速度变化较为明显突出,加速度变化能够反映轴承的振动情况。内圈和滚动体作为2个运动元件,它们高速旋转,振动很大,在剥落的冲击下,加速度的变化也是比较明显的,因此选用外圈剥落轴承模型的计算结果进行振动特征分析。为了更明显地凸显振动特征,接触力也能更真实有效地反映两个物体之间力的变化,选择剥落轴承处的滚动体,代号为3号体,为了对比明显,取剥落邻处为4号体,图6为3号体与4号体分别与内外圈z向接触力的变化曲线。分别选择正常内圈和外圈剥落下内圈的加速度信号,经过FFT转换,可以得到频域方面的特征。图7所示为正常内圈与外圈剥落时内圈的加速度信号分析结果,图8所示为正常滚动体与外圈剥落时滚动体的加速度信号分析结果。

图6 滚动体对内外圈的接触力

图7 正常(a)与剥落(b)的内圈加速度信号分析

图8 正常(a)与剥落(b)的滚动体加速度信号分析
对比图6(a)和图6(b)发现:正常体与内外圈接触力变化比较杂乱,随着速度与摩擦力的不断改变,导致振动的力也随机变化;而故障的3号体与内外圈接触力变化在0.065 s附近较为明显。原因是在有限周期内滚动体经过剥落处而产生,而在其他时段都是较为平稳的振动变化。同理,从4号滚动体上也能观察出正常时段振动为平稳和随机振动变化,而故障体表现为明显的冲击段,冲击后随即又恢复为平稳振动,并且体现一定的周期性。从正常与故障滚动体与内外圈的z向接触力曲线变化能体现出基本的振动特征。
从图7可以看出:内圈的加速度在一个固定间隔频率处会出现一次峰值,这表明此加速度存在一个波动周期,而且比较稳定。这个固定周期和内圈的旋转周期有关,当采样点通过某一位置时,出现最大峰值。但在频域范围内,没有表现特别明显的变化。外圈剥落时内圈加速度变化无明显规律,表明外圈剥落对内圈加速度的变化影响很小。同理,对外圈剥离故障下滚动振动加速度选取与分析,经过FFT时频转换得到图8。
结合角接触球轴承的系列相关参数和设置的内圈转速68 r/min,利用式(1)可以求出当外圈存在剥落故障时,外圈故障特征频率的理论值为491.3 Hz。由图8(b2)可知:在频率490.3 Hz附近幅值较大,反映了轴承的非正常运转状态,也表明滚子的振动量较大,且此频率与理论值491.3 Hz较吻合,故可以判断实际故障特征频率为490.3 Hz,其故障频率相对误差仅为0.203 5%。表明外圈剥落的仿真信号经过处理可以用于故障识别与检测。
3 模型验证
文中通过滚动体的理论计算速度与仿真模拟结果比较,分析2种方法的误差,来判断模型系数设置的合理性和方法的可行性。依照高速滚动球轴承各元件的运动学关系,外圈是全约束的,内圈进行高速旋转,因此滚动体的公转和自转速度大小分别为
(2)
(3)
(4)
其中:ω为内圈的旋转转速;D为轴承节圆直径;d为滚动体直径;ωc为滚动体轨道速度;ωr为滚动体绕自身轴线的转速;α为角位置。因此将角接触球轴承的各元件参数代入公式(2)(3)(4)中,并按照内圈速度为4 100 r/min,解出滚动体公转转速为1 752 r/min,自身旋转速度为13 386.5 r/min。
动态仿真要用到瞬态动力学分析模块,同时会伴随能量耗散的问题,各部件间的相互作用使得模拟速度下降,因此要控制沙漏,使轴承内圈的模拟速度达到要求转速。从内圈和滚动体节点的位移变化和速度变化,都可以计算出元件的转速。
考虑到滚动体的自转与公转比较复杂繁琐的问题,文中将先对内圈进行模型验证,能够更直观更方便地证明此模型的准确性。从图9(a)可以得出:内圈的旋转周期T为0.014 6 s,换算成转速为4 100 r/min,达到要求转速。可以看出后续内圈周期略微有些增大,表明内圈的速度在下降,原因是部件间的复杂力学效应导致能量的耗散。对比内圈位移曲线图9(a1)与内圈速度曲线图9(a2)发现,内圈节点位姿变化正好和设置的速度基本吻合,说明仿真能够实现转速的模拟[15]。

图9 轴承元件位移速度曲线
滚动体的x向位移和速度时间曲线分别如图9(b1)与图9(b2)所示,当内圈转速达到模拟速度时,由位移的变化曲线可知滚动体的公转周期约为0.034 s,转速为1 764 r/min,与理论转速1 752 r/min相差0.68%;由速度的变化曲线可知滚动体自转周期为0.003 93 s,滚动体的自转转速约为15 267.1 r/min,与13 386.5 r/min相差10%左右。由于滚动体运动中受力复杂,滚动体的运动是由内圈的摩擦驱动的,同时也会受到外圈摩擦的阻碍。由于仿真结果与理论值的误差较小,文中建立的动态有限元模型是可靠的,可用于轴承动态特性分析。
4 结论
文中利用ANSYS Workbench软件建立了H7009C型角接触球轴承的动力学有限元模型,分析了应力、接触力以及加速度对轴承振动特性的影响,得出以下结论:
(1)高速滚动球轴承的各元件中滚动体承担的应力最高,滚动轴承剥离增加了轴承的最大应力,最大应力首要出现在滚动体中,次之出现在保持架中,这也成为滚动体与保持架极易受损的原因之一。
(2)当剥落故障发生时,滚动体对内圈与外圈的z向接触力较正常轴承运转时期有明显增大的趋势,表现为冲击明显、振动剧烈,有明显的振动特征。
(3)通过对正常与外圈剥落下的内圈与滚动体加速度分析,发现外圈剥落对内圈加速度的变化影响很小,但对滚动体的加速度幅值影响较大,所研究轴承故障特征频率为490.3 Hz。该研究为角接触球轴承外圈剥落缺陷的检测提供了理论依据。
